Floor deformation control for roof cutting and pressure relief in gob-side entry retaining of deep buried mines
-
摘要: 目前有关巷道底鼓的研究与实践主要探讨巷道底板的变形机理及控制技术，对沿空留巷切顶卸压前后底板力学分析不全面。针对该问题，基于煤体分区破坏特征构建了切顶前后巷道围岩和底板力学模型，分析实体煤、巷旁支护及采空区对底板的作用，获得切顶前后巷道底鼓解析解，得出巷旁煤帮弹塑性区、巷道支护体及顶板下沉区底板所受载荷共同影响巷道底鼓量大小。采用数值模拟验证切顶卸压前后沿空留巷围岩破坏特征、应力分布及底鼓量变化，结果表明：切顶卸压技术可有效缩小巷道实体煤侧面及顶部的破坏区域，维持巷道围岩结构稳定；巷道底板最大应力、巷旁支护阻力、巷道底鼓量均下降，平均降幅分别为25.78%，56.14%，54.07%。现场应用结果表明，厚硬顶板沿空留巷底鼓量由709.345 1 mm降至320.965 8 mm，切顶卸压技术可以优化巷道围岩应力结构，抑制巷道底鼓，有效改善底板破坏情况。Abstract: Currently, research and practice on roadway floor heave mainly explore the deformation mechanism and control technology of roadway floor. The mechanical analysis of floor before and after roof cutting and pressure relief in gob-side entry retaining is not comprehensive. In order to solve the above problem, mechanical models of the surrounding rock and floor of the roadway before and after roof cutting are constructed based on the features of coal partition failure. The effects of solid coal, roadway support, and goaf on the floor are analyzed. The analytical solutions for the floor heave of the roadway before and after roof cutting are obtained. The conclusion is drawn that the elastic-plastic zone of the coal wall beside the roadway, the support structure of the roadway, and the load on the floor of the subsidence zone jointly affect the magnitude of the roadway floor heave. Numerical simulation is used to verify the features of rock mass failure, stress distribution, and changes in floor heave in gob-side entry retaining before and after roof cutting and pressure relief. The results show that roof cutting and pressure relief technology can effectively reduce the damage area on the solid coal side and top of the roadway, and maintain the stability of the roadway rock mass structure. The maximum stress of the roadway floor, the resistance of the roadway side support, and the amount of roadway floor heave all decrease, with an average decrease of 25.78%, 56.14%, and 54.07%, respectively. The on-site application results show that the amount of floor heave of thick hard top in gob-side entry retaining is reduced from 709.345 1 mm to 320.965 8 mm. The roof cutting and pressure relief technology can optimize the stress structure of the surrounding rock of the roadway, suppress the floor heave of the roadway, and effectively improve the floor damage.
-
0. 引言
在厚硬顶板沿空留巷条件下，受掘进和采动影响，巷道底板变形，出现底鼓。随着工作面推进，基本顶在采空区上方形成悬顶[1]。一旦发生顶板旋转下沉，会对煤岩体和巷旁支护造成冲击挤压[2]，加剧巷道底板变形[3]。底鼓现象造成巷道断面减小，阻碍设备运输、人员行走，影响工作面正常回采，增加大量维修工作和维护费用。切顶卸压技术可以在巷道采空区一侧形成预裂切缝面[4]，切断采空区和巷道顶板之间的联系，改善巷道围岩结构，减少底板变形量。因此，根据切顶卸压前后的围岩结构变化进一步研究巷道底鼓的变形机理具有一定意义。
针对沿空留巷切顶卸压的底板变形问题，学者们进行了大量研究。康志鹏等[5]以厚煤层软底留巷为背景，提出对底板进行合适的让压，以实现巷道柔性支护。于光远等[6]提出通过“切顶卸压+柔性让压+补强锚索控顶+双控锚杆控帮”的方式控制底鼓，取得了较好的效果。何满潮等[7]针对深部高应力复合破碎顶板切顶留巷，设计了一种新型可缩U型钢挡矸结构，可有效控制巷道底板变形。张幼振[8]提出了巷道底鼓机械化治理的技术思路和机械化施工系统的配置原则，研发了巷道修复机、底板锚固钻机等专用主导机械设备，可有效治理巷道底鼓。申斌学等[9]提出了切顶卸压柔模墙支护沿空留巷技术，在切顶后使用该技术可以对巷道顶板进行强力支护，抑制巷道底鼓。张宇旭等[10]通过试验证明了底板注浆与锚杆锚索联合支护可以改善底板应力状态，控制底板位移。以上有关巷道底鼓研究与实践主要探讨巷道底板的变形机理及控制技术，对沿空留巷切顶卸压前后底板力学分析不全面。针对上述问题，本文建立了巷道围岩和底板力学模型，分析各区域对巷道底板的作用，并推导了沿空留巷切顶前后巷道底鼓变形量计算公式。
1. 工程背景
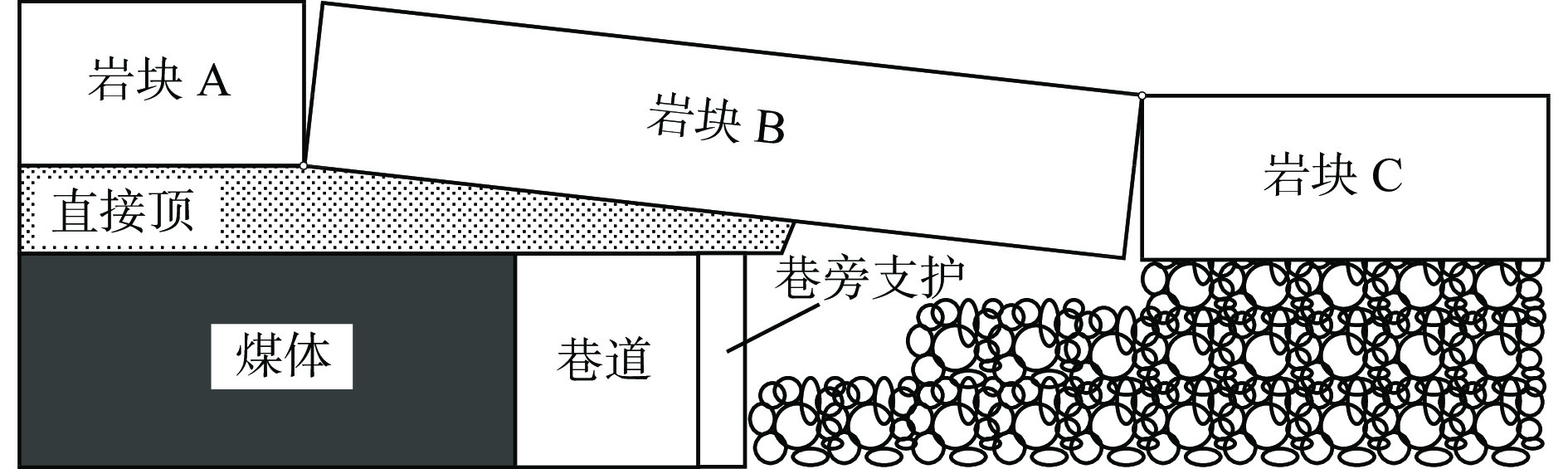
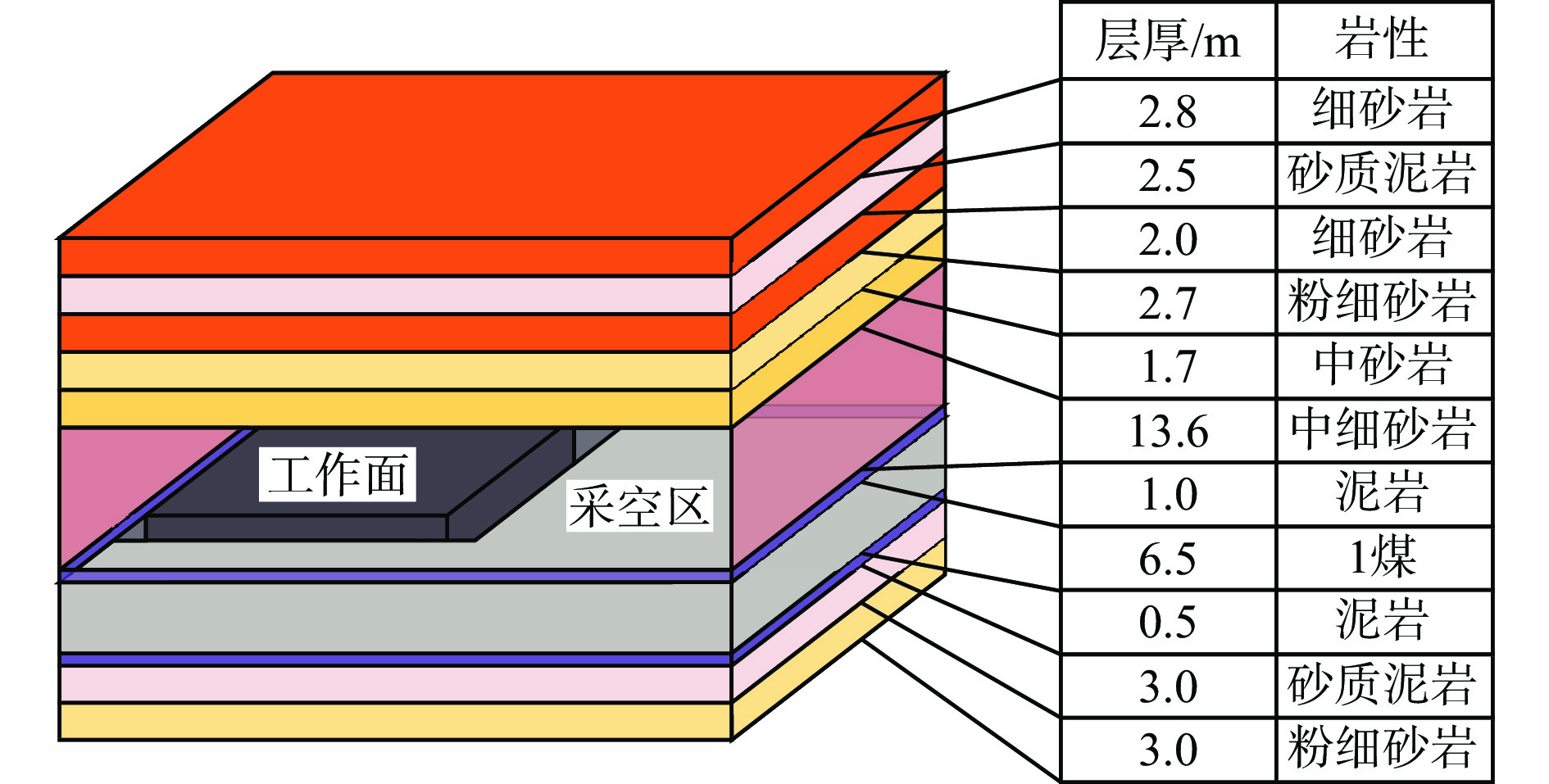
以淮南某矿沿空留巷工作面为研究对象，工作面长210 m，走向长1 784 m，1号煤厚3.5～8.5 m，平均厚度为6.5 m。煤层倾角为6～8°，平均值为7°。工作面煤层直接顶主要为泥岩，平均厚1 m；基本顶主要为中细砂岩，平均厚13.6 m；直接底主要为泥岩，平均厚0.5 m；基本底主要为砂质泥岩，平均厚3.0 m。工作面布置及岩性特征如图1所示。
![]()
图 1 沿空留巷工作面布置及岩性特征Figure 1. Arrangement of gob-side entry retaining working face and lithological characteristics2. 巷道底鼓力学分析
2.1 沿空留巷围岩结构
工作面开挖后，因直接顶极薄且强度较低，采空区直接顶垮落，基本顶在实体煤体侧断裂。巷旁支护体在顶板载荷作用下产生变形，压缩下沉。此时顶板处于给定变形状态[11]，如图2所示，巷旁支护体主要承受直接顶及悬露基本顶岩块B的重力。上覆岩层破断岩块A，B，C三者相互铰接形成承压结构[12]，承载上覆岩层压力并控制下方巷道的围岩稳定。岩块C下沉后，在上覆岩层载荷作用下与矸石接触发生挤压，并逐渐被压实[13]。
2.2 围岩结构力学分析
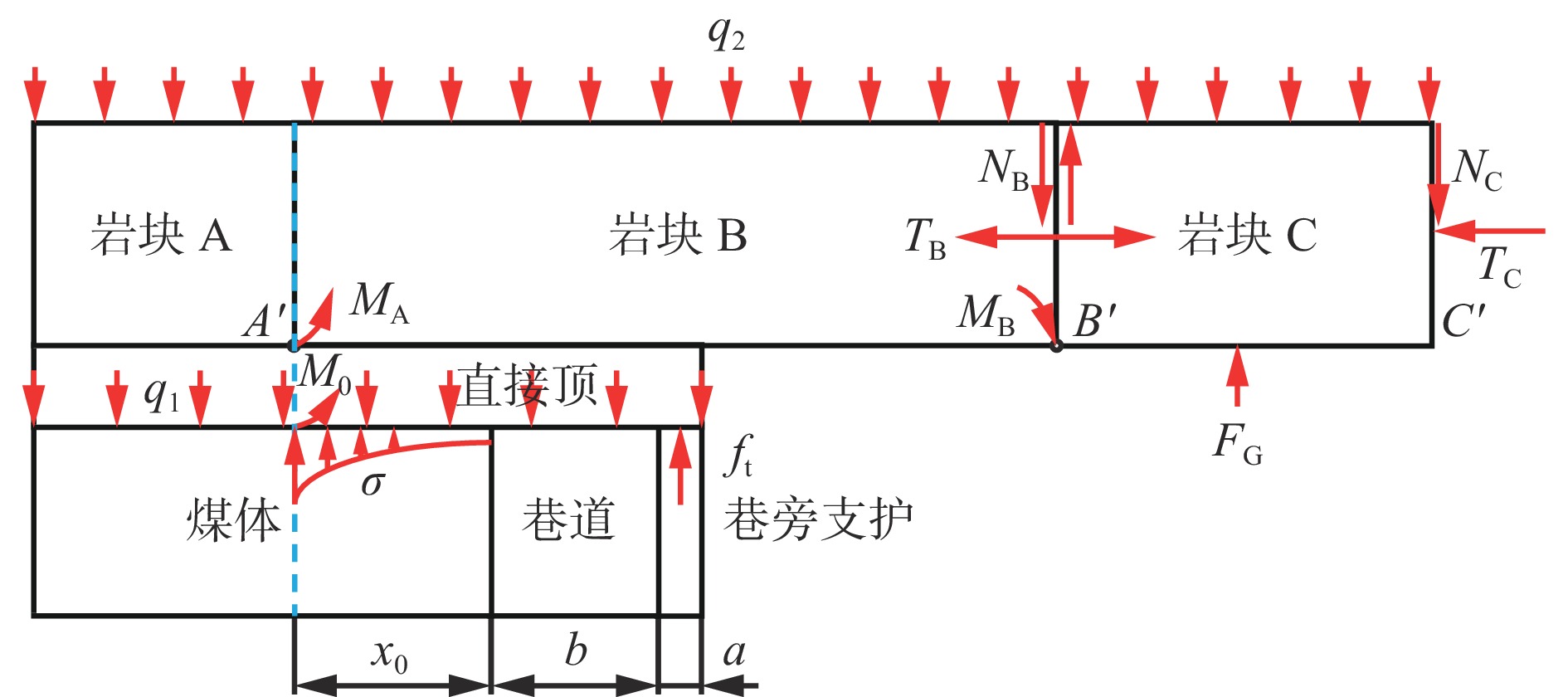
在给定变形条件下，侧向实体煤承担围岩应力峰值，巷旁支护体无法有效控制基本顶，岩块B发生旋转下沉。对沿空留巷顶板力学模型作如下假设：① 基本顶于实体煤侧弹塑性交界处断裂，绕直接顶向采空区侧旋转倾斜。② 采空区矸石对岩块C产生支撑力，对岩块B支撑力为0[14]。③ 忽略直接顶、基本顶及更上位岩层之间的剪切力。④ 基本顶上覆岩层载荷均匀施加在基本顶上。⑤ 巷内支护的变形忽略不计[15]。根据假设条件，建立沿空留巷力学模型，如图3所示。
基本顶沿实体煤弹塑性区交界处上方$ {A}' $点断裂并向采空区旋转，煤体极限平衡区宽度x0[16]及塑性区煤体对顶板的支撑力σ分别为
$$ {x_0} = \dfrac{{{h_{\rm{c}}}\lambda }}{{2\tan\; \varphi }}\ln\;{\dfrac{{k\gamma {H} + {c}/{{\tan\; \varphi }}}}{{{c}/{{\tan\; \varphi }} + {{{p_{\rm{x}}}}}/{\lambda }}}} $$ (1) $$ \sigma = \left( {\dfrac{c}{{\tan\; \varphi }} + \dfrac{{{p_{\rm{x}}}}}{\lambda }} \right){\exp\left({\dfrac{{2x_0\tan\; \varphi }}{{{h_{\rm{c}}}\lambda }}}\right)} - \dfrac{c}{{\tan\; \varphi }} $$ (2) 式中：hc为煤层厚度；λ为煤体侧压系数；φ为煤层界面内摩擦角；k为煤帮侧应力集中系数；γ为岩层平均容重；H为开采深度；c为煤层界面黏聚力；px为煤帮侧向支护阻力。
基本顶沿倾向垮落长度L与垮落步距l[17]分别为
$$ \left\{ \begin{gathered} l = h\sqrt {{{2{R_{\rm{T}}}}}/{{{q_2}}}} \\ L = l\left( { {l}/{S} + \sqrt {{{{l^2}}}/{{{S^2}}} + {3}/{2}} } \right) \\ \end{gathered} \right. $$ (3) 式中：h为基本顶岩层厚度；RT为基本顶抗拉强度；q2为基本顶载荷；S为基本顶沿工作面悬露长度。
岩块C水平方向受力取0，可得
$$ {T_{\rm{B}}} = {T_{\rm{C}}} = \dfrac{{{q_2}{L^2}}}{{2(h - \Delta {S_{\rm{ B}}})}} $$ (4) 式中：TB为岩块B在$ {B}' $处所受水平推力；TC为岩块C在$ {C}' $处所受水平推力；$ \Delta {S}_{\rm{ B}} $为岩块B在$ {B}' $处的下沉量。
岩块C垂直方向受力取0，可得
$$ {N_{\rm{B}}} + {F_{\rm{G}}} = {N_{\rm{B}}} + {K_{\rm{G}}}L = {N_{\rm{C}}} + {q_2}L $$ (5) 式中：$ {N}_{\rm{B}} $，$ {N}_{\rm{C}} $分别为岩块B，C所受剪切力；FG为采空区矸石对基本顶的支撑力；$ {K}_{\rm{G}} $为采空区矸石支撑系数。
$ {B}' $点力矩取0，可得
$$ {M_{\rm{B}}} + {T_{\rm{C}}}(h - \Delta {{S}_{\rm{ C}}}) + {F_{\rm{G}}}L/2 - {N_{\rm{C}}}L - {q_2}{L^2}/2 = 0 $$ (6) $$ {N_{\rm{C}}} = \dfrac{{{M_{\rm{B}}} + {T_{\rm{B}}}(h - \Delta {{S}_{\rm{ C}}}) - {q_2}{L^2}/2}}{L} + {F_{\rm{G}}}/2 $$ (7) $$ {N_{\rm{B}}} = \dfrac{{{M_{\rm{B}}} + {T_{\rm{B}}}(h - \Delta {{S}_{\rm{ C}}}) + {q_2}{L^2}/2}}{L} - {F_{\rm{G}}}/2 $$ (8) 式中MB为岩块B在$ {B}' $处的残余弯矩。
对于岩块B，$ {A}' $点力矩取0，可得
$$ \begin{split} &{M_{\rm{A}}} + {M_0} + {f_{\rm{t}}}(a + b + {x_0}) + \int_0^{{x_0}} \sigma ({x_0} - x){\mathrm{d}}x +{T_{\rm{B}}}(h - \Delta {{S}_{\rm{ B}}}) - \\ &\qquad {M_{\rm{B}}} - {q_2}{l^2}/2 - {q_1}({x_0} + a + b)^2/2 -{N_{\rm{B}}}l = 0 \\[-5pt] \end{split} $$ (9) 式中：MA为岩块A在$ {A}' $处的残余弯矩；M0为直接顶对基本顶的抗弯弯矩；ft为巷旁支护阻力；a为巷旁支护体宽度；b为巷道宽度；x为模型中任一点的横坐标；q1为直接顶载荷。
联立式（3）、式（4）、式（8）、式（9）得
$$ \begin{split} {f_{\rm{t}}} =& \left\{ {} \right.2{M_{\rm{B}}} + {q_2}{L^2} + {q_1}{\left( {{x_0} + a + b} \right)^2}/2 + \\ & {q_2}{L^2}\left( {\Delta {{S}_{\rm{ B}}} - \Delta {{S}_{\rm{ C}}}} \right)/\left[ {2\left( {h - \Delta {{S}_{\rm{ B}}}} \right)} \right] - {F_{\rm{G}}}L/2 - {M_{\rm{A}}} - \\ & {M_0} - \int_0^{{x_0}} {\sigma \left( {{x_0} - x} \right){\rm{d}}x} \left. {} \right\}/ \left( {{x_0} + b + a/2} \right) \end{split} $$ (10) 式中$ \Delta {S}_{\rm{ C}} $为岩块C在$ {C}' $处的下沉量。
2.3 巷道底板受力分析
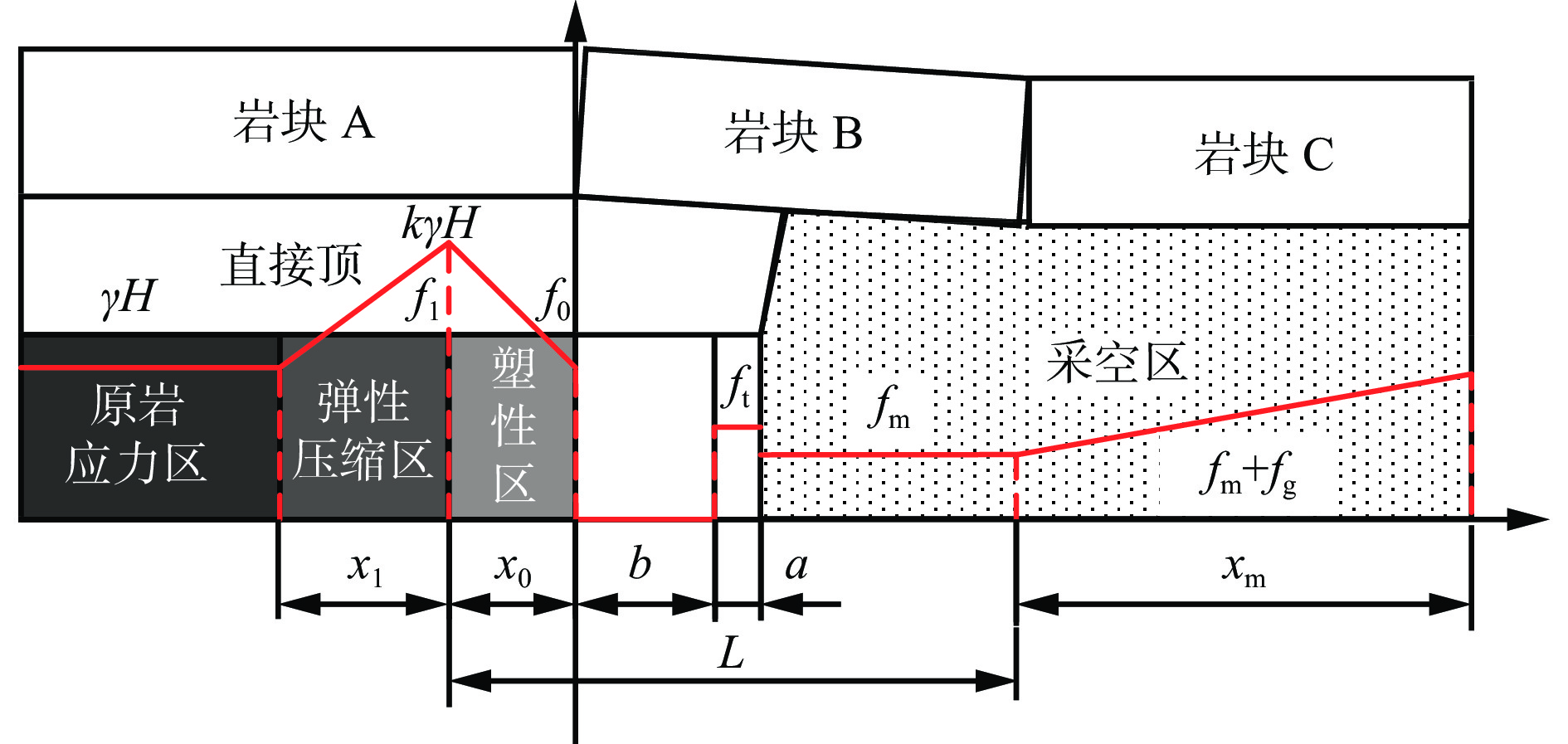
顶板垮落后，底板应力重新分布。为了简化计算，假设煤帮弹性区、塑性区的垂直应力呈线性分布，沿工作面走向方向取剖面，建立沿空留巷底板力学模型，如图4所示。fg为顶板破断岩块对底板的作用力；xm为顶板旋转下沉区宽度；fm为冒落矸石的重力；x1为弹性压缩区宽度；f0，f1分别为塑性区、弹性压缩区煤体对底板的作用力。
实体煤塑性区作用在底板的力为
$$ {f_0} = {{\left( {k - 1} \right)\gamma H}}\left( {{x_0} - x} \right)/{{{x_0}}} \quad - {x_0} \leqslant x \leqslant 0 $$ (11) 实体煤的弹性压缩区和塑性区共同承担了上覆岩层载荷和采动引起的应力重新分布，因此$ \left({x}_{1}+ {x}_{0}\right)\left(k+1\right)\gamma H/2=\gamma H{S}_{ 0}/2 $，S0为工作面长度，则
$$ {x_1} = {{{S_{ 0}}}}/{{(k + 1)}} - {x_0} $$ (12) 实体煤弹性压缩区作用在底板的力为
$$ {f_1} = {{\left( {k - 1} \right)\gamma H}}\left( {x - {x_1}} \right)/{{({x_1} - {x_0})}} \quad - {x_0} - {x_1} \leqslant x \leqslant - {x_0} $$ (13) 直接顶垮落矸石对底板的作用力为
$$ {f_{\text{m}}} = {h_1}{\gamma _1} $$ (14) 式中：h1为直接顶岩层厚度；γ1为直接顶岩层容重。
上方基本顶岩块C垮落后，沿倾向逐渐将矸石堆压实。顶板旋转下沉区宽度[18]为
$$ {x_{\rm{m}}} = h\cot\; \delta + L $$ (15) 式中δ为基本顶的破断角[19]。
$$ \delta=45^{\circ}-\dfrac{1}{2}\varphi_2+\dfrac{1}{2}\arctan l\sqrt{\dfrac{R_{\rm{T}}}{q_2}} $$ (16) 式中φ2为基本顶内摩擦角。
顶板破断下沉岩块对底板的作用力为
$$ {f_{\rm{g}}} = {{2{F_{\rm{G}}}}}\left[ {x - \left( {L - {x_0}} \right)} \right]/{{x_{\rm{m}}^2}} $$ (17) 2.4 巷道底板变形分析
引用等效载荷概念[20]，以消除原岩应力$\gamma H$对底板变形的影响。建立沿空留巷底板等效载荷分布力学模型，如图5所示。
![]()
图 5 沿空留巷底板等效载荷分布力学模型Figure 5. Mechanical model of equivalent load distribution on the floor of gob-side entry retaining在半无限平面边界上，点I所受应力为原岩应力，设垂直位移为0，将该点设为基点，则分布载荷q（x）在边界上点J（横坐标为xJ）处的垂直位移[21-22]为
$$ {\mathrm{d}}{U_{{J}}} = \dfrac{{2q\left( x \right)}}{{{\text{π}} {E_{\rm{d}}}}}\ln \dfrac{s}{\rho }{\mathrm{d}}\rho $$ (18) 式中：UJ为点J处的底鼓量；Ed为巷道底板岩层弹性模量；s为基点I到q（x）的距离；ρ为点J到q（x）的距离。
将不同分布载荷在J处引起的垂直位移相加，求得J处的底鼓量：
$$ \begin{split} {U_{{J}}} =& \dfrac{2}{{{\text{π}} {E_{\rm{d}}}}}\Bigg[\int_{ - \left( {{x_0} + {x_1}} \right)}^{ - {x_0}} {\left( {{f_1} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} + \int_{ - {x_0}}^0 {\left( {{f_0} - \gamma H} \right)} \\ &\ln \dfrac{s}{\rho }{\rm{d}}x +\int_b^{b + a} {\left( {{f_{\rm{t}}} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} + \int_{b + a}^{L - {x_0}} {({f_{\rm{m}}} - } \gamma H) \\ &\ln \dfrac{s}{\rho }{\rm{d}}x +\int_{L - {x_0}}^{L - {x_0} + {x_{\rm{m}}}} {\left( {{f_{\rm{m}}} + {f_{\rm{g}}} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} \Bigg]\\[-5pt] \end{split} $$ (19) 3. 切顶卸压对沿空留巷围岩结构影响
3.1 切顶卸压围岩结构力学分析
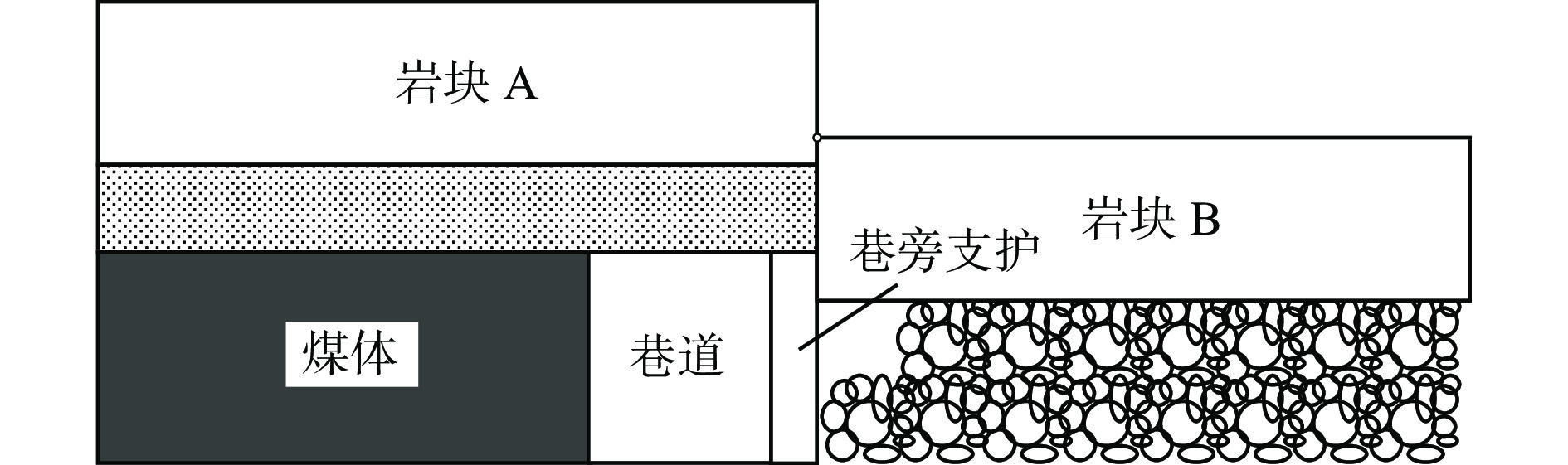
通过预爆破切顶，基本顶沿切顶缝断裂，侧向悬臂梁长度大幅减小，在巷道上方形成短臂梁结构[23]。由于直接顶厚度极薄，垮落后形成的矸石堆不足以充填整个采空区并支撑上覆岩层，所以采空区上方破断基本顶沿切缝大幅下沉并压实下方矸石堆。切顶后沿空留巷围岩结构如图6所示。
![]()
图 6 切顶后沿空留巷围岩结构Figure 6. Surrounding rock structure of gob-side entry retaining after roof cutting对切顶后沿空留巷顶板力学模型作如下假设：① 切顶角度为90°，简化力学模型。② 采空区侧基本顶沿切缝直接断裂垮落，岩块下沉时旋转角度为0。③ 垮落后的矸石堆积在采空区，对下沉基本顶起到支撑作用[24]。④ 忽略直接顶、基本顶及更上位岩层之间的剪切力。⑤ 基本顶上覆岩层载荷均匀施加在基本顶上。⑥ 巷内支护的变形忽略不计。⑦ 实体煤弹塑性区域及煤层底板所受应力在切顶前后的变化较覆岩整体的运移程度小，故忽略不计。
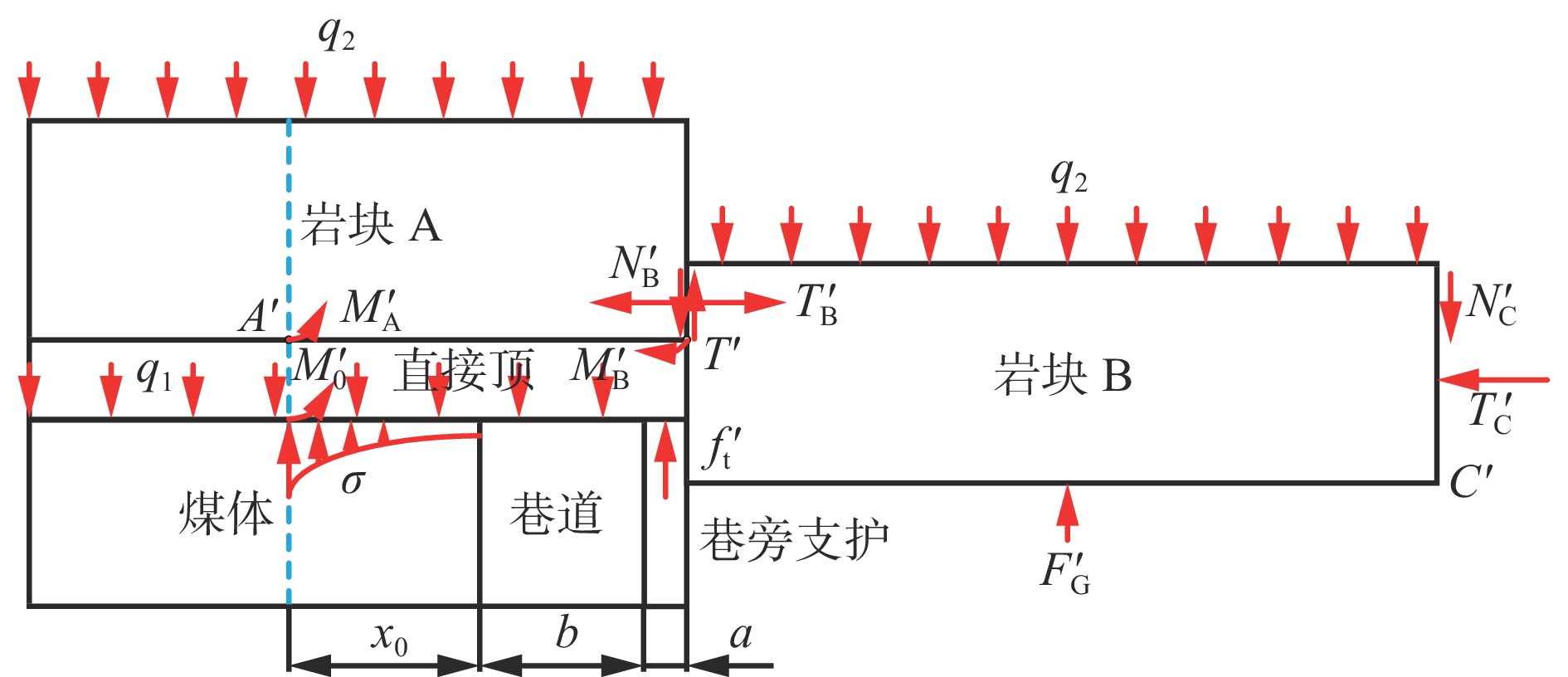
根据假设，构建切顶后沿空留巷力学模型，如图7所示。$ {T}_{\rm{B}}' $为岩块A在$ {B}' $处所受水平推力；$ {T}_{\rm{C}}' $为岩块B在$ {C}' $处所受水平推力；$ {N}_{\rm{B}}' $，$ {N}_{\rm{C}}' $分别为岩块A，B受到的剪切力；$ {M}_{\rm{A}}' $为岩块A在$ {A}' $处产生的弯矩；$ {M}_{\rm{B}}' $为岩块B在$ {B}' $处的残余弯矩；$ {f}_{\rm{t}}' $为切顶后巷旁支护阻力；$ {F}_{\rm{G}}' $为切顶后采空区矸石对基本顶支撑力。
![]()
图 7 切顶后沿空留巷力学模型Figure 7. Mechanical modeling of gob-side entry retaining after roof cutting根据静力平衡可得
$$ {N'_{\rm{C}}} = \dfrac{{{M'_{\rm{B}}} + {{T}'_{\rm{C}}}(h - \Delta {{S}'_{\rm{C}}}) - q{L^2}/2}}{L} + {F'_{\rm{G}}}/2 $$ (20) $$ {N'_{\rm{B}}} = \dfrac{{{M'_{\rm{B}}} + {{T}'_{\rm{C}}}(h - \Delta {{S}'_{\rm{C}}}) + q{L^2}/2}}{L} - {F'_{\rm{G}}}/2 $$ (21) $$ {T'_{\rm{C}}} = \dfrac{{{q_2}{L^2}}}{{2(h - \Delta {S'_{\rm{C}}})}} $$ (22) 式中$ \Delta {S}_{\rm{ C}}' $为岩块B在$ {C}' $处的下沉量。
$$ {\begin{split} {f'_{\rm{t}}} =& [{M'_{\rm{B}}}(L + {x_0} + a + b)/L + {q_2}{({x_0} + a + b)^2}/2 + {q_2}L({x_0} +\\ & a + b)/2 + {q_1}{({x_0} + a + b)^2}/2 - {{F}'_{\rm{G}}}({x_0} + a + b)/2 -\\ & {M'_{\rm{A}}} - {M_0} - \int_0^{{x_0}} \sigma ({x_0} - x){\rm{d}}x]/({x_0} + b + a/2) \end{split}} $$ (23) 3.2 切顶卸压巷道底板变形分析
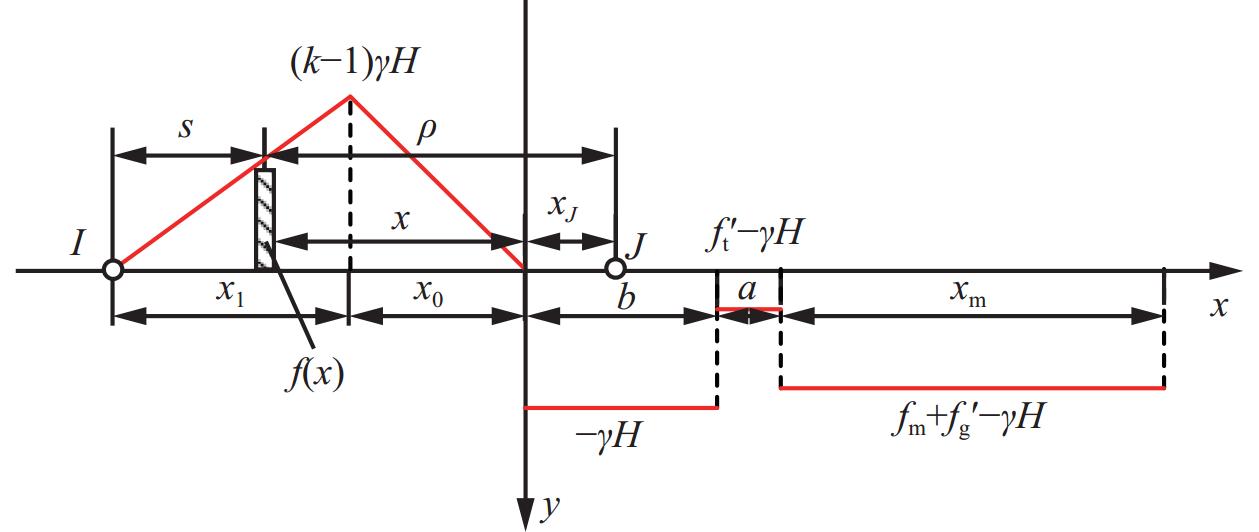
切顶后沿空留巷底板等效载荷分布力学模型如图8所示。
![]()
图 8 切顶后沿空留巷底板等效载荷分布力学模型Figure 8. Mechanical model of equivalent load distribution on the floor of gob-side entry retaining after roof cutting切顶后顶板破断岩块对底板作用力为
$$ {f'_{\rm{g}}} = {F'_{\rm{G}}} = {K'_{\rm{G}}}L $$ (24) 式中$ {K}_{\rm{G}}' $为切顶后采空区矸石支撑系数。
底板上M点的底鼓量为
$${\begin{split} {U'_{\rm{M}}} =& \dfrac{2}{{{\text{π}} {E_{\rm{d}}}}}\Bigg[\int_{ - \left( {{x_0} + {x_1}} \right)}^{ - {x_0}} {\left( {{f_1} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} + \int_{ - {x_0}}^0 {\left( {{f_0} - \gamma H} \right)} \ln \dfrac{s}{\rho }{\rm{d}}x + \\ & \int_0^{b + a} {\left( {{f'_{\rm{t}}} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} + \int_{b + a}^{b + a + {x_{\rm{m}}}} {\left( {{f_{\rm{m}}} + {f'_{\rm{g}}} - \gamma H} \right)\ln \dfrac{s}{\rho }{\rm{d}}x} \Bigg] \\ \end{split}} $$ (25) 4. 切顶卸压底鼓数值模拟研究
4.1 模型的建立
采用Mohr-Coulomb本构模型，从现场获取巷道围岩岩体试样，按照相关要求制备成相应的标准试件。各岩层物理力学参数见表1。
表 1 各岩层物理力学参数Table 1. Physical and mechanical parameters of each rock formation岩性 弹性模
量/GPa抗拉强
度/MPa内摩擦
角/（°）泊松比 容重/
（kN·m−3）黏聚
力/MPa细砂岩 42 6.50 25 0.16 27.0 5.4 粉细砂岩 18 2.35 31 0.21 26.0 3.8 中砂岩 12 2.11 28 0.22 26.2 3.3 泥岩 6 1.47 24 0.21 22.5 2.4 1煤 0.8 1.20 21 0.35 13.8 1.8 砂质泥岩 9 2.91 24 0.23 25.2 2.8 根据地质资料建立立体模型，模拟在上一工作面回采完毕后，接替回采1615A工作面时，切顶卸压对巷道底板变形的控制效果。
4.2 沿空留巷巷道演化特征
4.2.1 切顶卸压巷道围岩破坏分布特征及应力分析
沿走向取剖面，切顶卸压前后工作面处破坏分布特征如图9所示。可看出工作面回采时采空区上方形成弹塑性破坏区域，且随工作面的推进逐渐向高位岩层发育，由破坏形态可知采空区上覆中位岩层逐渐趋于稳定。巷道实体煤侧及顶部围岩在切顶卸压后，破坏区域显著减小。随着工作面的推进，采用切顶卸压技术可有效缩小巷道实体煤侧面及顶部的破坏区域，维持巷道围岩结构稳定。
![]()
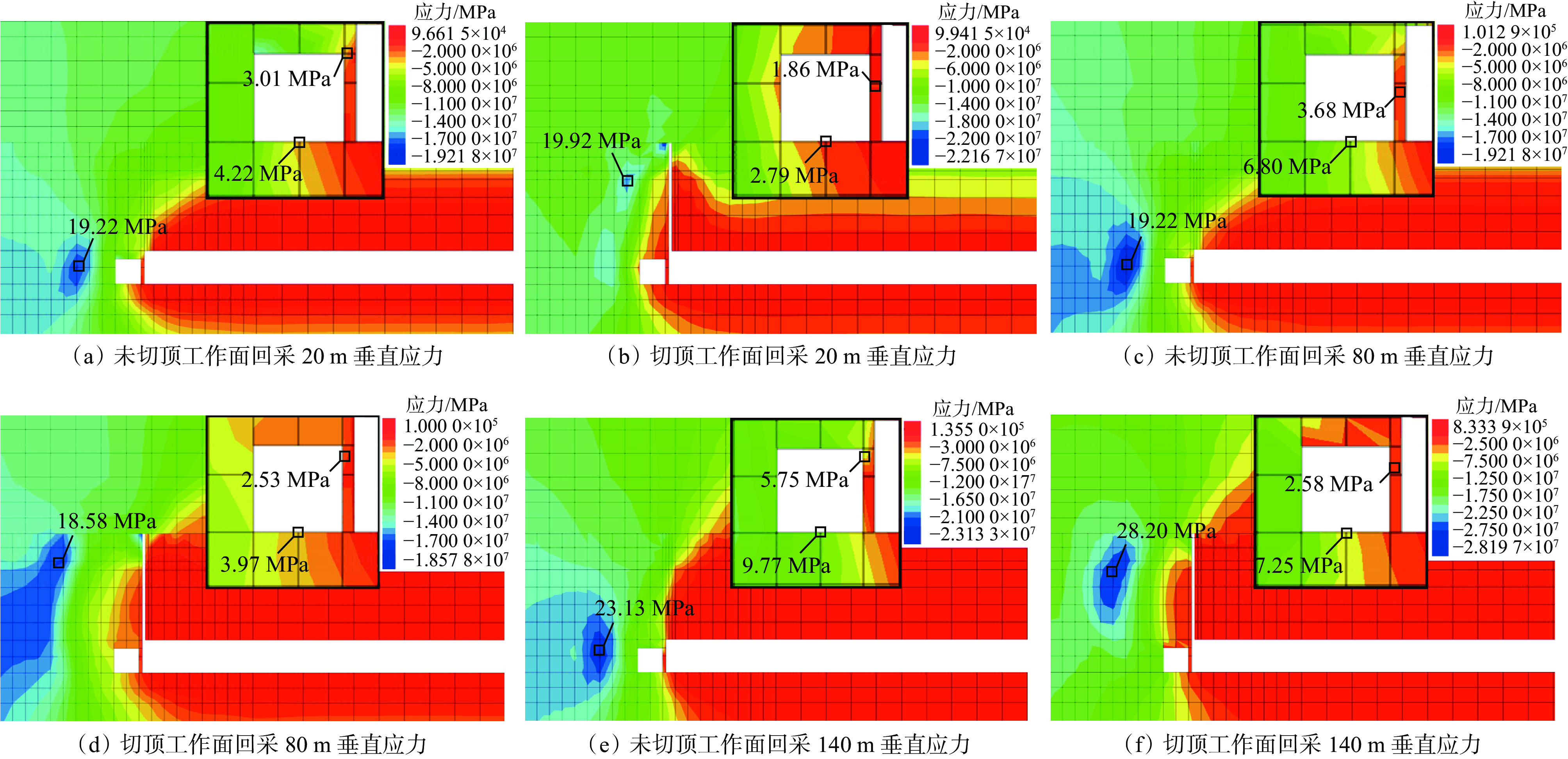
图 9 切顶卸压前后工作面破坏分布特征对比Figure 9. Comparison of damage distribution characteristics of the working face before and after roof cutting and pressure relief沿走向取剖面，切顶卸压前后工作面处垂直应力如图10所示。可看出：切顶卸压前，巷道实体煤侧出现应力集中现象，应力峰值随着工作面推进由19.22 MPa增加至23.13 MPa，巷旁支护阻力峰值为5.75 MPa，巷道底板中部应力峰值为9.77 MPa，对巷道围岩稳定造成严重影响；切顶卸压后，应力集中向巷道顶板上方及深部转移，远离巷道围岩，应力峰值由19.92 MPa增加至28.20 MPa，巷旁支护阻力峰值减少至2.58 MPa，巷道底板中部应力峰值为7.25 MPa，巷道顶板区域所受应力显著减小。采用切顶卸压技术可有效优化巷道围岩应力结构，巷旁支护阻力降幅为56.14%，底板最大应力平均降幅为25.78%。
![]()
图 10 切顶卸压前后工作面垂直应力对比Figure 10. Comparison of vertical stress on the working face before and after roof cutting and pressure relief4.2.2 切顶卸压巷道底鼓分析
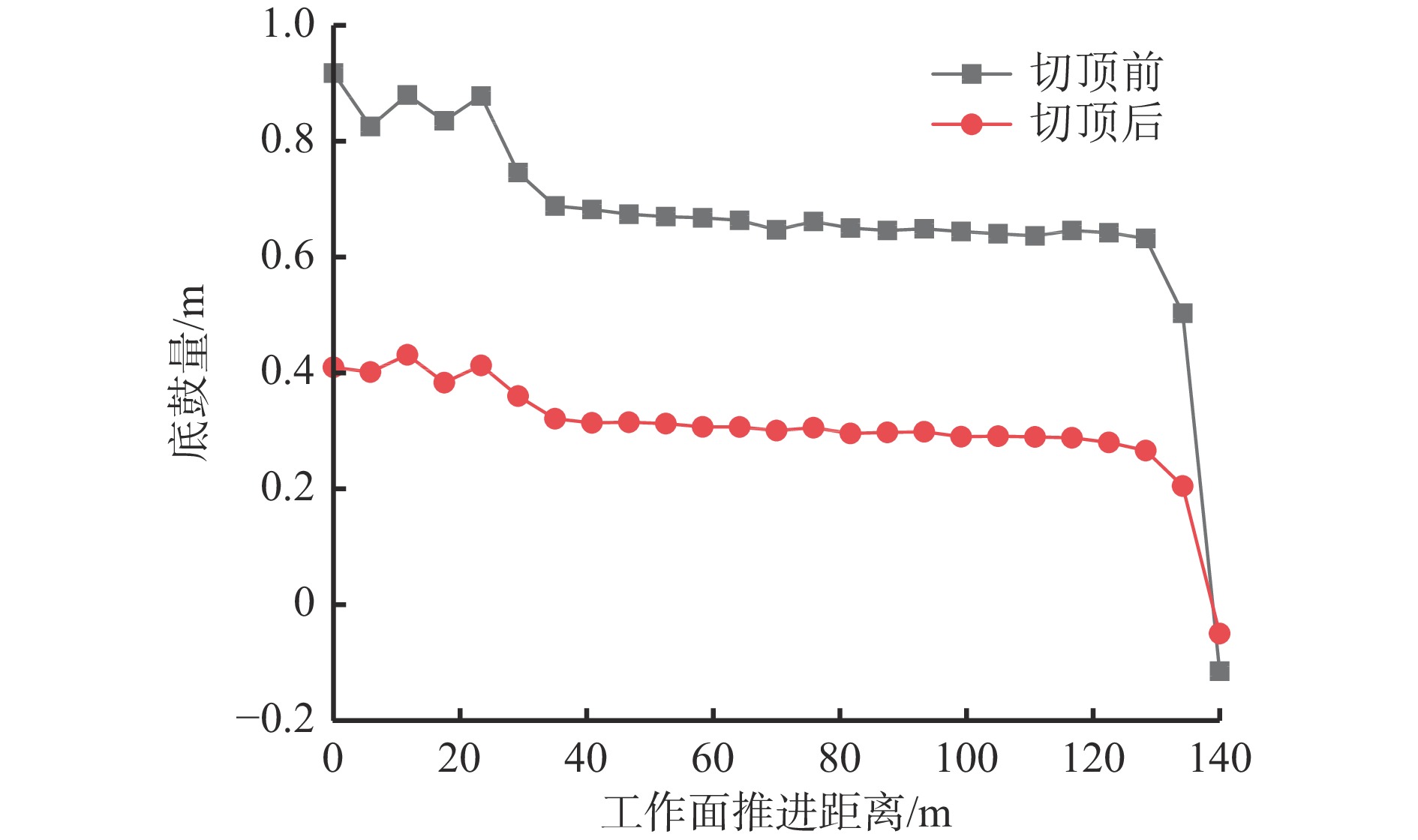
对整条巷道底板变形量进行监测，结果如图11所示。可知切顶前，工作面超前处巷道底板变形量在503～917 mm波动，均值为664 mm；切顶后，工作面超前处巷道底板变形量在204～409 mm波动，均值为305 mm，较切顶前下降54.07%。沿空留巷切顶卸压有效缓解了沿空留巷底鼓。
![]()
图 11 工作面推进切顶卸压前后巷道底鼓对比Figure 11. Comparison of floor heave before and after roof cutting and pressure relief5. 工程应用
预裂切缝钻孔深12 m，切缝角度为15°。采用双向聚能爆破预裂技术，切缝距煤帮100 mm，切缝孔间距为500 mm。特质聚能管外径为42 mm，内径为36.50 mm，管长1 500 mm。炮空底部装药量为3～5卷，炮孔处为1～2卷，炸药规格为ϕ35×330 mm/卷。现场炮孔布置如图12所示。
结合现场数据对巷道底鼓解析解进行验证。基本参数：hc=6.5 m，h=13.6 m，px=0.1 MPa，φ=24°，H=600 m，γ=25 kN/m3，c=2.4 MPa，k=2.6，S0=200 m，Ed=9.0 GPa，η=0.9，KP0=1.10，a=1 m，b=5 m。
其他参数设置：直接顶及基本顶载荷根据q=γh确定；垮落长度L=20 m；岩梁断裂处残余弯矩为0；$ \Delta {S}_{\rm{ B}}=\Delta {S}_{\rm{ C}} $；实体煤塑性区宽度x0=10.3 m；切顶前后采空区矸石对基本顶支撑力FG=5.237 MN，$ {F}_{\rm{G}}' $=10.532 MN；切顶前后巷旁支护阻力ft=5.564 5 MN，$ {f}_{\rm{t}}' $=2.194 2 MN。
将上述参数代入式（19）、式（25），可得切顶前后巷道底鼓量$ {U}_{\rm{M}}=-709.345\;1\;\mathrm{m}\mathrm{m} $，$ {U}_{\rm{M}}'=320.965\;8\;\mathrm{m}\mathrm{m} $。
切顶前后沿空留巷底鼓情况如图13所示。可看出沿空留巷切顶后，巷道底鼓量减小，切顶卸压有效改善巷道底板破坏情况。
![]()
图 13 切顶前后沿空留巷底鼓情况Figure 13. Condition of the floor heave in the gob-side entry retaining before and after roof cutting6. 结论
1） 针对工作面现场情况，运用给定变形理论，构建了沿空留巷顶板岩层力学模型，推导出切顶卸压前后巷旁支护阻力的计算方法。
2） 运用弹性力学知识，结合底板各区域所受载荷，推导出切顶卸压前后巷道底鼓计算公式。分析得出巷旁煤帮弹塑性区、巷道支护体及顶板下沉区底板所受载荷共同影响巷道底鼓量大小。
3） 切顶卸压后，应力集中现象向巷道顶板上方及深部转移，巷道底板最大应力平均降幅为25.78%，巷旁支护阻力平均降幅为56.14%；厚硬顶板沿空留巷底鼓量由709.345 1 mm降至320.965 8 mm。切顶卸压技术可以优化巷道围岩应力结构，抑制巷道底鼓，有效改善底板破坏情况。
-
![]()
图 1 沿空留巷工作面布置及岩性特征
Figure 1. Arrangement of gob-side entry retaining working face and lithological characteristics
![]()
图 5 沿空留巷底板等效载荷分布力学模型
Figure 5. Mechanical model of equivalent load distribution on the floor of gob-side entry retaining
![]()
图 6 切顶后沿空留巷围岩结构
Figure 6. Surrounding rock structure of gob-side entry retaining after roof cutting
![]()
图 7 切顶后沿空留巷力学模型
Figure 7. Mechanical modeling of gob-side entry retaining after roof cutting
![]()
图 8 切顶后沿空留巷底板等效载荷分布力学模型
Figure 8. Mechanical model of equivalent load distribution on the floor of gob-side entry retaining after roof cutting
![]()
图 9 切顶卸压前后工作面破坏分布特征对比
Figure 9. Comparison of damage distribution characteristics of the working face before and after roof cutting and pressure relief
![]()
图 10 切顶卸压前后工作面垂直应力对比
Figure 10. Comparison of vertical stress on the working face before and after roof cutting and pressure relief
![]()
图 11 工作面推进切顶卸压前后巷道底鼓对比
Figure 11. Comparison of floor heave before and after roof cutting and pressure relief
![]()
图 13 切顶前后沿空留巷底鼓情况
Figure 13. Condition of the floor heave in the gob-side entry retaining before and after roof cutting
表 1 各岩层物理力学参数
Table 1 Physical and mechanical parameters of each rock formation
岩性 弹性模
量/GPa抗拉强
度/MPa内摩擦
角/（°）泊松比 容重/
（kN·m−3）黏聚
力/MPa细砂岩 42 6.50 25 0.16 27.0 5.4 粉细砂岩 18 2.35 31 0.21 26.0 3.8 中砂岩 12 2.11 28 0.22 26.2 3.3 泥岩 6 1.47 24 0.21 22.5 2.4 1煤 0.8 1.20 21 0.35 13.8 1.8 砂质泥岩 9 2.91 24 0.23 25.2 2.8 
下载: 导出CSV
-
[1] 潘立友,唐鹏,周脉来,等. 悬顶结构巷道冲击地压防控研究[J]. 煤炭科学技术,2022,50(4):42-48. PAN Liyou,TANG Peng,ZHOU Mailai,et al. Research on prevention and control of rock burst in entry with suspended roof structure[J]. Coal Science and Technology,2022,50(4):42-48.
[2] 何满潮,陈上元,郭志飚,等. 切顶卸压沿空留巷围岩结构控制及其工程应用[J]. 中国矿业大学学报,2017,46(5):959-969. HE Manchao,CHEN Shangyuan,GUO Zhibiao,et al. Control of surrounding rock structure for gob-side entry retaining by cutting roof to release pressure and its engineering application[J]. Journal of China University of Mining & Technology,2017,46(5):959-969.
[3] 杨鸿智, 鞠文君, 王东攀, 等. 综放工作面沿空留巷 “错动” 变形破坏机制及其控制[J]. 采矿与安全工程学报,2023,40(2):224-231. YANG Hongzhi, JU Wenjun, WANG Dongpan, et al. The "relative movement" deformation mechanism and control technique of gob-side entry retaining in top-coal caving mining[J]. Journal of Mining & Safety Engineering,2023,40(2):224-231.
[4] 马新根,何满潮,李先章,等. 切顶卸压自动成巷覆岩变形机理及控制对策研究[J]. 中国矿业大学学报,2019,48(3):474-483. MA Xingen,HE Manchao,LI Xianzhang,et al. Deformation mechanism and control measures of overlying strata with gob-side entry retaining formed by roof cutting and pressure releasing[J]. Journal of China University of Mining & Technology,2019,48(3):474-483.
[5] 康志鹏,段昌瑞,余国锋,等. 厚煤层软底沿空留巷围岩变形特征分析及顶帮强化支护技术[J]. 工矿自动化,2022,48(11):101-109. KANG Zhipeng,DUAN Changrui,YU Guofeng,et al. Analysis on deformation characteristics of surrounding rock of gob-side entry retaining with soft bottom in thick coal seam and strengthening support technology of roof and side[J]. Industry and Mine Automation,2022,48(11):101-109.
[6] 于光远,王炯,孙晗,等. 砌块充填沿空留巷底鼓大变形机理及综合控制技术[J]. 采矿与安全工程学报,2022,39(2):335-346. YU Guangyuan,WANG Jiong,SUN Han,et al. Mechanism and comprehensive control techniques for large deformation of floor heave in block filling gob-side entry retaining[J]. Journal of Mining & Safety Engineering,2022,39(2):335-346.
[7] 何满潮, 马资敏, 郭志飚, 等. 深部中厚煤层切顶留巷关键技术参数研究[J]. 中国矿业大学学报,2018,47(3):468-477. HE Manchao, MA Zimin, GUO Zhibiao, et al. Key parameters of the gob-side entry retaining formed by roof cutting and pressure release in deep medium-thickness coal seams[J]. Journal of China University of Mining & Technology,2018,47(3):468-477.
[8] 张幼振. 煤矿巷道底鼓机械化治理技术应用研究[J]. 煤炭科学技术,2018,46(1):93-98. ZHANG Youzhen. Applied study on mechanized control technology of floor heave in mine roadway[J]. Coal Science and Technology,2018,46(1):93-98.
[9] 申斌学, 周宏范, 朱磊, 等. 深井复合顶板切顶卸压柔模墙支护沿空留巷技术[J]. 工矿自动化,2021,47(11):101-106. SHEN Binxue, ZHOU Hongfan, ZHU Lei, et al. The technology of gob-side entry retaining supported by flexible formwork wall with roof cutting and pressure relief for composite roof in deep mine[J]. Industry and Mine Automation,2021,47(11):101-106.
[10] 张宇旭,王科. 煤巷底鼓破坏特征及支护技术研究[J]. 工矿自动化,2019,45(6):73-79,85. ZHANG Yuxu,WANG Ke. Research on failure characteristics of floor heave and support technology in coal roadway[J]. Industry and Mine Automation,2019,45(6):73-79,85.
[11] 黄万朋,高延法,文志杰,等. 钢管混凝土支柱巷旁支护沿空留巷技术研究[J]. 中国矿业大学学报,2015,44(4):604-611. HUANG Wanpeng,GAO Yanfa,WEN Zhijie,et al. Technology of gob-side entry retaining using concrete-filled steel tubular column as roadside supporting[J]. Journal of China University of Mining & Technology,2015,44(4):604-611.
[12] 王亚军,何满潮,张科学,等. 无煤柱自成巷开采巷道矿压显现特征及控制对策[J]. 采矿与安全工程学报,2018,35(4):677-685. WANG Yajun,HE Manchao,ZHANG Kexue,et al. Strata behavior characteristics and control countermeasures for the gateroad surroundings in innovative non-pillar mining method with gateroad formed automatically[J]. Journal of Mining & Safety Engineering,2018,35(4):677-685.
[13] 朱珍,张科学,袁红平. 切顶卸压沿空留巷碎石巷帮控制技术及应用[J]. 煤炭科学技术,2018,46(3):25-32. ZHU Zhen,ZHANG Kexue,YUAN Hongping. Control technology and its application of roadway side wall formed by gangue in gob-side entry retaining formed by roof cutting and pressure releasing[J]. Coal Science and Technology,2018,46(3):25-32.
[14] 冯超,刘少伟,张小东,等. 切顶条件下综放沿空留巷充填体承载特征及合理宽度研究[J]. 采矿与安全工程学报,2023,40(2):232-242. FENG Chao,LIU Shaowei,ZHANG Xiaodong,et al. Study on the bearing characteristics and reasonable width of the backfilling body for gob-side entry in fully-mechanized top-coal caving face under the roof cutting condition[J]. Journal of Mining & Safety Engineering,2023,40(2):232-242.
[15] 朱永建,任恒,王平,等. 倾斜厚层坚硬顶板条件下沿空留巷稳定性控制[J]. 中南大学学报(自然科学版),2023,54(3):956-966. ZHU Yongjian,REN Heng,WANG Ping,et al. Stability control of gob-side entry retention under the condition of inclined thick layer and hard roof[J]. Journal of Central South University (Science and Technology),2023,54(3):956-966.
[16] 郑西贵,安铁梁,郭玉,等. 原位煤柱沿空留巷围岩控制机理及工程应用[J]. 采矿与安全工程学报,2018,35(6):1091-1098. ZHENG Xigui,AN Tieliang,GUO Yu,et al. Surrounding rock control mechanism and engineering application of in situ coal pillar in gob-side entry retaining[J]. Journal of Mining & Safety Engineering,2018,35(6):1091-1098.
[17] 陈磊. 基于弹性基础梁模型的来压步距确定[J]. 煤矿安全,2017,48(5):49-52. CHEN Lei. Determination of weighting interval based on elastic foundation beam model[J]. Safety in Coal Mines,2017,48(5):49-52.
[18] 华心祝,李迎富. 沿空留巷底板变形力学分析及底臌防控[J]. 煤炭学报,2016,41(7):1624-1631. HUA Xinzhu,LI Yingfu. Mechanics analysis on floor deformation of gob-side entry retaining and prevention and control of floor heave[J]. Journal of China Coal Society,2016,41(7):1624-1631.
[19] 许斌,蒋金泉,代进,等. 采场上覆关键层破断角的力学推导和实验模拟[J]. 煤炭学报,2018,43(3):599-606. XU Bin,JIANG Jinquan,DAI Jin,et al. Mechanical derivation and experimental simulation of breaking angle of key strata in overlying strata[J]. Journal of China Coal Society,2018,43(3):599-606.
[20] 马念杰,侯朝炯. 采准巷道矿压理论及应用[M]. 北京:煤炭工业出版社,1995. MA Nianjie,HOU Chaojiong. The underground pressure of sectional roadways and its control[M]. Beijing:China Coal Industry Publishing House,1995.
[21] 徐芝纶. 弹性力学简明教程[M]. 3版. 北京:高等教育出版社,2002. XU Zhilun. A concise course in elasticity[M]. 3rd ed. Beijing:Higher Education Press,2002.
[22] 周道祥,张伟林. 工程弹性力学基础[M]. 合肥:合肥工业大学出版社,2006. ZHOU Daoxiang,ZHANG Weilin. Fundamentals of engineering elasticity[M]. Hefei:Hefei Univerisity of Technology Publishing House,2006.
[23] 何满潮,高玉兵,杨军,等. 无煤柱自成巷聚能切缝技术及其对围岩应力演化的影响研究[J]. 岩石力学与工程学报,2017,36(6):1314-1325. HE Manchao,GAO Yubing,YANG Jun,et al. An energy-gathered roof cutting technique in no-pillar mining and its impact on stress variation in surrounding rocks[J]. Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1314-1325.
[24] 陆银龙,韩磊,吴开智,等. 特厚煤层沿空掘巷力源结构特征与围岩协同控制策略[J]. 中国矿业大学学报,2024,53(2):238-249. LU Yinlong,HAN Lei,WU Kaizhi,et al. Characteristics of stress sources and comprehensive control strategies for surrounding rocks of gob-side driving entry in extra thick coal seam[J]. Journal of China University of Mining & Technology,2024,53(2):238-249.
-
期刊类型引用(3)
1. 李刚，刘航，迟国铭，石占山，范永君. 大柳塔煤矿沿空留巷柔模砼墙支护阻力核定及失稳判据研究. 工矿自动化. 2025(01): 145-155 . 
本站查看
2. 吕彦国. 深孔爆破切顶卸压沿空留巷支护技术研究. 建井技术. 2024(06): 1-7 . 百度学术
3. 孟国龙. 某深部煤层综采工作面切顶卸压留巷技术研究. 现代矿业. 2024(12): 48-51+59 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 93
- HTML全文浏览量: 36
- PDF下载量: 22
- 被引次数: 3
