Research on decoupling control method for single-phase cascade H-bridge rectifier in coal mine scenarios
-
摘要: 针对单相级联H桥整流器的电力电子设备在煤矿场景下运行过程中直流侧存在二次电压纹波，导致网侧电流畸变、电容值漂移等问题，通过分析单相级联H桥整流器直流侧二次电压纹波的形成原因，提出了一种基于分裂电容不相等的独立型解耦拓扑的优化控制方法。该方法通过在电容两端叠加二倍工频的电压来抵消二次电压纹波，实现了直流侧二次电压纹波的有效抑制。针对3种基于构造二次电压的解耦方式（直流分裂电容值不等，直流电压分量相等；直流分裂电容值不等，且直流电压分量也不等；直流分裂电容值相等，直流电压分量不等）进行了参数设计和控制策略的研究，并通过分析参数对二次电压幅值的影响，确定了最优的参数取值范围，以实现有效的功率解耦，并减小电容值，降低设备体积和成本。仿真结果表明：① 在0.2 s时加入分裂电容的独立型解耦拓扑（SC−IAPD）电路，基于解耦方式2的SC−IAPD电路控制方法、基于解耦方式2的SC−IAPD电路的优化控制方法、基于解耦方式1的 SC−IAPD电路控制方法的直流侧输出电压纹波都控制在1～1.5 V，说明对称半桥解耦电路可有效抑制直流电压波动，同时在负荷变化时具有良好的解耦性能。② 在轻载切重载的情况下，基于解耦方式2的SC−IAPD电路的优化控制方法能快速跟随负载变化，实现纹波的抑制，具有更强的带载能力和更佳的解耦效果。而在重载切轻载的情况下，基于解耦方式1的 SC−IAPD电路控制方法能够更好地实现解耦性能，将电压纹波控制在1 V以内。如果考虑电容值的最小化，基于解耦方式2的SC−IAPD电路的控制方法则更具优势。实验结果表明：① 负载突变前，传统控制方法和基于二次电压的解耦控制方法都能有效抑制直流侧的电压纹波，但基于二次电压的解耦控制方法在抑制电压纹波方面效果更佳，使直流侧的电压纹波更小。② 负载突变后，传统控制方法无法维持直流侧电压的稳定性，出现较大的震荡，失去稳定性。Abstract: In response to the problems of secondary voltage ripple on the DC side of single-phase cascade H-bridge rectifiers during operation in coal mine scenarios, such as grid side current distortion and capacitance drift, this paper analyzes the causes of secondary voltage ripple on the DC side of single-phase cascade H-bridge rectifiers and proposes an optimization control method based on an independent decoupling topology with unequal split capacitors. This method effectively suppresses the secondary voltage ripple on the DC side by overlaying twice the power frequency voltage on both ends of the capacitor to counteract the secondary voltage ripple. A study is conducted on parameter design and control strategies for three decoupling methods based on constructing secondary voltage (DC split capacitor with unequal capacitance values and equal DC voltage components; DC split capacitor with unequal capacitance values and unequal DC voltage components; DC split capacitor with equal capacitance values and unequal DC voltage components). By analyzing the influence of parameters on the amplitude of secondary voltage, the optimal parameter range is determined to achieve effective power decoupling, reduce capacitance values, and lower equipment volume and cost. The simulation results show the following points. ① The split capacitor IAPD (SC-IAPD) is added at 0.2 s, SC-IAPD circuit control method based on decoupling method 2, SC-IAPD circuit optimization control method based on decoupling method 2, and SC-IAPD circuit control method based on decoupling method 1 all control the DC side output voltage ripple at 1-1.5 V. This indicates that the symmetrical half bridge decoupling circuit can effectively suppress DC voltage fluctuations and has good decoupling performance when load changes. ② In the case of light load switching to heavy load, the optimized control method of SC-IAPD circuit based on decoupling method 2 can quickly follow the changes in load, achieve ripple suppression, and have stronger load carrying capacity and better decoupling effect. In the case of heavy load switching to light load, the SC-IAPD circuit control method based on decoupling method 1 can better achieve decoupling performance, controlling voltage ripple within 1 V. If we consider minimizing the capacitance value, the control method of SC-IAPD circuit based on decoupling method 2 is more advantageous. The experimental results show the following points. ① Before the sudden change of load, both traditional control methods and decoupling control methods based on secondary voltage can effectively suppress the voltage ripple on the DC side. However, decoupling control methods based on secondary voltage have better effects in suppressing voltage ripple, resulting in smaller voltage ripple on the DC side. ② After a sudden change in load, traditional control methods cannot maintain the stability of the DC side voltage, resulting in significant oscillations and loss of stability.
-
0. 引言
煤矿负荷多为大功率交直流传动设备，需消耗电网里大量的无功功率，且大容量、高功率非线性电力电子装置的广泛引用，使煤矿电网谐波问题越来越严重。在煤矿场景下通常采用无功补偿方法解决上述问题，具有无功补偿功能的设备包括静止同步补偿器（Static Synchronous Compensator，STATCOM））、静止无功发生器（Static Var Generator，SVG）、储能变流器（Power Conversion System, PCS）及高压变频器等，其核心组成部分为电力电子变换器[1-2]。随着矿井自动化及智能化的不断发展，为了满足电力调峰、辅助动态运行、系统调频及防爆的需要，对电力电子变换器的灵活可控性、高效性及可靠性提出了更高要求[3]。
多电平变换器以其在交直流电源转换上的灵活性和高度的可控性，广泛应用于煤矿场景下的各类电力电子设备中[4-5]。传统的两电平或三电平变换器虽然可以采用器件串联和功率单元并联等技术提高多电平输出，进一步扩展应用场合，但会带来设计复杂、均流困难及可靠性低等问题[6-7]。单相级联H桥变换器（Single-phase Cascaded H-Bridge Rectifier，SCHBR）因其易于模块化、输出波形质量好和易于输出多电平等优点，被广泛应用于可再生能源及煤矿电力系统等领域[8-9]。然而CHBR的固有工作特性会导致直流侧存在较大的二次电压纹波，从而降低系统效率及设备寿命[10]。
为了提高电力电子变换器在煤矿应用场景下的稳定性，国内外学者从SCHBR直流侧二次电压纹波抑制和拓扑结构方面展开研究。在SCHBR直流侧二次电压纹波抑制方面，文献[11]在各子模块直流侧并联无源滤波网络，加入LC谐振回路，以吸收直流侧的二次功率脉动，产生稳定的直流侧电压，但存在系统整体体积较大、效率较低、使用寿命较短的缺点[12-13]。文献[14]通过把3倍频零序电压叠加到调制波上，使2倍频波动转换为幅值更低的4倍频波动，从而实现对SCHBR直流侧二次电压纹波的抑制，然而该方法会引起网侧电流畸变。文献[15]提出了一种基于构造基频电压的控制方法，在2个分裂电容上施加直流偏置，并叠加1个幅值相等但相位相反的基频交流分量的电压，实现功率解耦，但直流侧会衍生出基频脉动功率，且网侧输入电流含有直流分量和二次谐波，极大地降低了系统的电能质量和效率[16]。在拓扑结构方面，有学者提出了附加开关器件电路的有源功率解耦（Active Power Decoupling，APD）方案[17-19]，以实现对直流侧二次电压纹波的抑制和提高能量转换系统的效率[20]。文献[21]通过在多电平直流/直流变换器中加入小型飞跨电容，来实现升压操作和二次功率纹波补偿，使典型的直流/直流变换器实现主动功率解耦控制，无需额外组件，从而降低体积、成本和变换器损耗。该控制方法具有良好的解耦效果，但是分裂电容由于介质损耗、湿度和时间效应等因素，会导致电容值发生漂移，尽管能补偿二次脉动功率，但直流侧会衍生出基频脉动功率。
上述研究虽然实现了功率解耦，但引入了网侧电流畸变、电容值漂移等问题，难以应用于煤矿实际场景。针对上述问题，本文提出了一种煤矿场景下SCHBR解耦控制方法。首先，建立SCHBR模型，分析了直流侧二次电压纹波的形成原因。然后，为抑制SCHBR的直流侧二次电压纹波，进而减小矿用电力电子设备的体积，提出了基于构造二次电压解耦的控制策略，对3种基于构造二次电压的控制方法进行了对比分析，并给出了其参数设计方法。最后，通过仿真验证了所提方法的可行性和有效性。
1. 矿用SCHBR直流电压二倍频波动
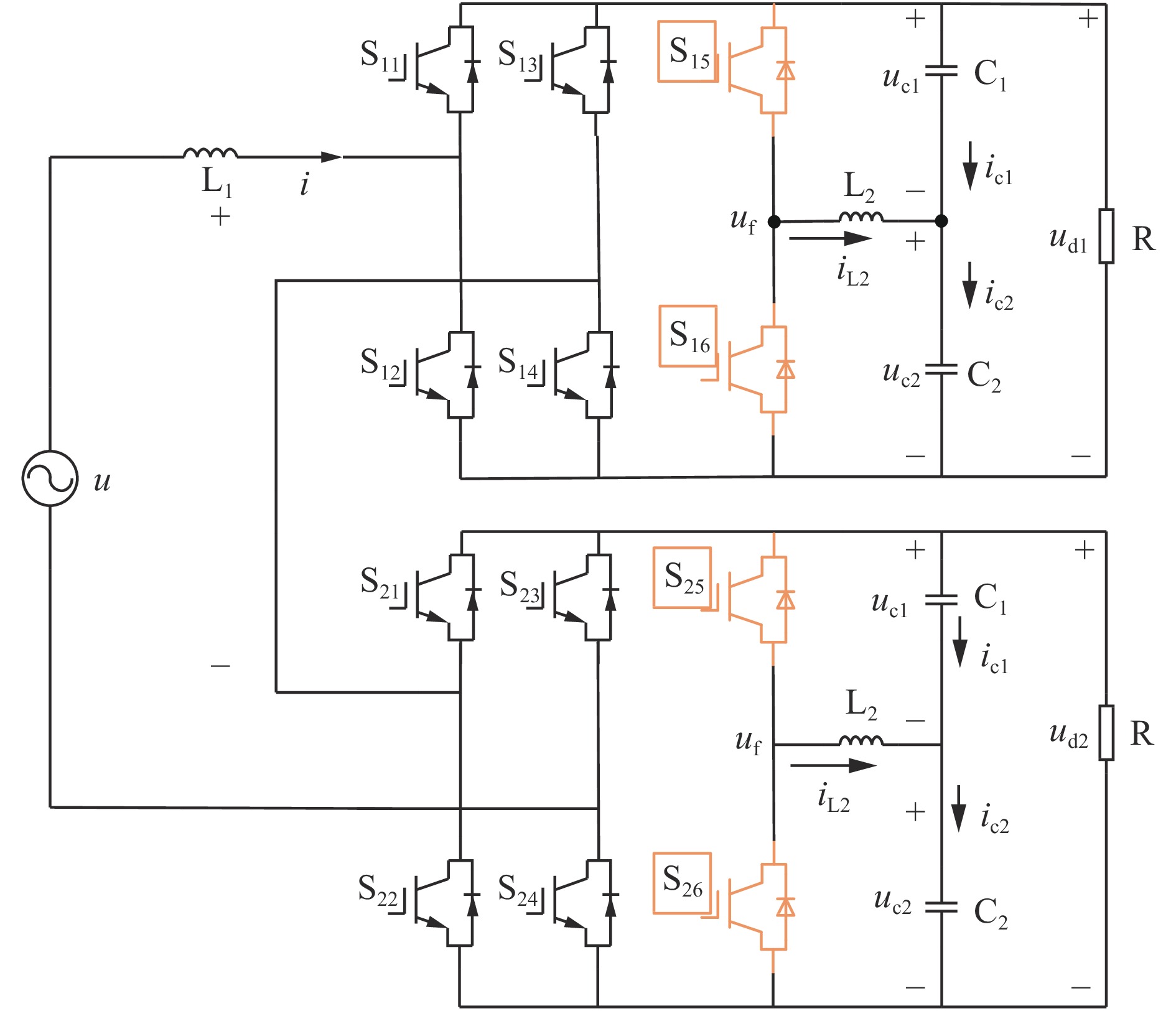
SCHBR广泛应用于煤矿级联SVG、矿用应急储能系统等场景中，以基于分裂电容的独立型解耦拓扑（Split Capacitor Independent Active Power Decoupling，SC−IAPD）的矿用SCHBR主电路拓扑（图1）为例，分析SCHBR的直流电压二倍频纹波产生的原因。图1中，u为网侧电压；i为网侧输入电流；L1为滤波电感；C1，C2为直流分裂电容；uc1，uc2分别为C1和C2两端电压；ic1和ic2分别为流经C1和C2的电流；L2为解耦电感；iL2为解耦电感电流；S11—S16，S21—S26为电力电子开关元件绝缘栅双极晶体管（Insulated GateBipolar Transistor, IGBT）；uf为L2两端电压；ud1，ud2为直流侧电压；R为限流电阻。对SCHBR直流侧的二次脉动功率进行分析，H桥的输入功率为
![]()
图 1 基于SC−IAPD的矿用SCHBR主电路拓扑Figure 1. Main circuit topology of mine single-phase cascaded H bridge rectifier（SCHBR） based on split capacitor IAPD （SC-IAPD）$$ \begin{gathered} {P_{{\text{in}}}} = P - {P_{{\mathrm{L}}1}} = {P_0} - {P_{\mathrm{r}}} = \frac{{UI}}{2}\cos \;\varphi - \\ \left[ {\frac{{UI}}{2}\cos \,(2\omega t + 2\theta {\text{ + }}\varphi ){\text{ + }}\frac{{\omega {L_1}{I^2}}}{2}\sin \,(2\omega t{\text{ + }}2\theta {\text{ + }}2\varphi )} \right] \\ \\ \end{gathered} $$ (1) 式中：P为网侧功率；PL1为L1的功率；P0为恒定功率；Pr为纹波功率；U，I分别为u和i的幅值；φ为电网电压与网侧电流之间的相角差；ω为电网的基频；t为时间；θ为u的初相角。
假设各级联H桥单元的直流侧电压相等，均为ud，在未投入功率解耦拓扑时，各单元直流侧总瞬时功率为
$$ {P_{\text{d}}} = N\frac{{{C_{\text{d}}}}}{2}\frac{{{\text{d}}u_{\text{d}}^2}}{{{\text{d}}t}} $$ (2) 式中：N为级联数；Cd为2个分裂电容等效为1个的电容。
由功率守恒定律可知Pin=Pd，则各级联H桥单元的直流侧电压为
$$ \begin{split} &{u_{\text{d}}} =\\ &\sqrt {{U_{\text{d}}} - \frac{{UI}}{{4N\omega {C_{\mathrm{d}}}}}\sin \,(2\omega t + 2\theta + \varphi ) + \frac{{\omega {L_1}{I^2}}}{{2N}}\sin \,(2\omega t + 2\theta + 2\varphi )} \end{split}$$ (3) 式中Ud为直流电压的恒定值。
从式（3）可看出，H桥单元的直流侧电压ud包括稳定分量和二次电压纹波分量。二次电压纹波分量产生的原因：① 单相系统本身存在固有的二次脉动功率。② 煤矿网侧电感引起功率波动，其波动程度受到交流侧电源角频率的影响。矿用SCHBR直流侧二次电压纹波会增加电容电流，使电容发热，降低设备寿命，但如果通过增大电容容量来抑制二倍频波动，会增大设备体积与成本。
2. 基于SC−IAPD构造的二次电压解耦控制方法
目前矿用电力电子设备的传统控制策略是在直流分裂电容值相等的理想情况下提出的，但在实际运行中，如果分裂电容值发生偏差，会导致直流侧电压出现基频脉动。传统的控制方法无法抑制直流侧电压的基频脉动，使得网侧电流出现直流分量和二次谐波分量，影响系统的正常运行。
在直流分裂电容的基准电压中引入二次谐波分量，可实现功率解耦控制，且对电容偏差不敏感。因此，本文将构造二次电压来修正电容电压参考值的思想加入控制算法中，基本思想在2个分裂电容上施加直流偏置，并叠加1个幅值相等但相位相反的二倍频交流分量的电压，使其产生的二次功率来补偿直流侧的二次脉动功率，避免出现基频脉动问题。修正后的2个分裂电容电压为
$$ \left\{ \begin{gathered} {u_{{\mathrm{c}}1}} = {U_{{\text{d}}1}} + {U_{\mathrm{c}}}\sin \,(2\omega t + \delta ) \\ {u_{{\mathrm{c}}2}} = {U_{{\text{d}}2}} - {U_{\mathrm{c}}}\sin \,(2\omega t + \delta ) \\ \end{gathered} \right. $$ (4) 式中：Ud1和Ud2为分裂电容的直流电压分量；Uc为二次电压幅值；δ为波动电压的初相位。
修正后流过电容C1的电流ic1和流过电容C2的电流ic2为
$$ \left\{ \begin{gathered} {i_{{\mathrm{c}}1}} = {C_1}\frac{{{\mathrm{d}}{u_{{\mathrm{c}}1}}}}{{{\mathrm{d}}t}} = 2\omega {C_1}{U_{\mathrm{c}}}\cos \,(2\omega t + \delta ) \\ {i_{{\mathrm{c}}2}} = {C_2}\frac{{{\mathrm{d}}{u_{{\mathrm{c}}2}}}}{{{\mathrm{d}}t}} = - 2\omega {C_2}{U_{\mathrm{c}}}\cos \,(2\omega t + \delta ) \\ \end{gathered} \right. $$ (5) 则SC−IAPD电路的瞬时功率Pd为
$$ \begin{split} {P_{\text{d}}} =& N\left({u_{{\mathrm{c}}1}}{i_{{\mathrm{c}}1}} + {u_{{\mathrm{c}}2}}{i_{{\mathrm{c}}2}} + {L_2}\frac{{{\mathrm{d}}{i_{{\mathrm{L}}2}}}}{{{\mathrm{d}}t}}{i_{{\mathrm{L}}2}}\right) =\\ & 2N\omega ({C_1}{U_{{\mathrm{d}}1}} - {C_2}{U_{{\mathrm{d}}2}}){U_{\mathrm{c}}}\cos \,(2\omega t + \theta ) +\\ & N\omega ({C_1} + {C_2}){U_{\mathrm{c}}^2}[1 - 4{L_2}{\omega ^3}({C_1} + {C_2})]{{\sin\,(4}}\omega t + 2\delta ) \end{split} $$ (6) SC−IAPD电路的瞬时功率不再包含一次功率分量，但含有2倍频功率和小幅值的4倍频功率。2倍频功率对交流侧的二次脉动功率进行补偿，从而实现SCHBR直流侧电压纹波的抑制。4倍频功率相较于2倍频功率幅值很小，可忽略不计。
为了抵消二次脉动功率，令式（1）和式（6）中的二次分量相等，可得
$$ \left\{ \begin{gathered} {U_{\mathrm{c}}} = \frac{{\sqrt {{{(UI)}^2} + 2\omega {L_2}U{I^3}\sin \varphi + {{(\omega {L_2}{I^2})}^2}} }}{{4N\omega ({C_1}{U_{{\mathrm{d}}1}} - {C_2}{U_{{\mathrm{d}}2}})}} \\ \delta = 2\theta + \varphi + \pi + \arctan \frac{{\omega {L_2}I\cos \varphi }}{{\omega {L_2}I\cos \varphi + UI}} \\ \end{gathered} \right. $$ (7) 根据式（7）可知，在直流分裂电容上分别叠加电压±Ucsin （2ωt+δ），在不增加矿用电力电子设备体积的情况下，抑制了直流侧二次电压纹波，减小了电容发热，增加了设备的可靠性。
3. 基于构造二次电压解耦的参数设计和控制策略
为了使分裂电容电压满足式（6），需采用特定的控制，消除矿用SCHBR的直流侧二次电压纹波。通过式（5）平衡H桥单元输入功率的二次纹波，则其二次波动分量不能为0，即C1Ud1−C2Ud2≠0。为满足该条件，可根据分裂电容值和直流偏置是否相等分为3种解耦方式，实现构造二次电压的解耦控制。
1） 解耦方式1：C1≠C2，Ud1=Ud2。设直流偏置系数为0.5，2个分裂电容的直流电压分量相等，即 Ud1=Ud2，仅使两直流分裂电容值不相等，从而产生二次功率来补偿交流侧的脉动功率，达到消除SCHBR直流侧二次电压纹波的目的。
2） 解耦方式2：C1≠C2，Ud1≠Ud2。使2个分裂电容值不相等，同时通过调制使2个分裂电容的直流电压分量也不相等，尽量增大C1Ud1−C2Ud2的值，从而产生更大的二次纹波功率，去抵消交流侧的脉动功率，增强解耦性能和整流器的带载能力。
3） 解耦方式3：C1=C2，Ud1≠Ud2。保持2个分裂电容值相等，仅通过将直流偏置系数引入半桥对称解耦电路控制中，使2个分裂电容的直流电压分量不等，从而产生二次功率，以补偿交流侧的二次脉动功率，达到抑制直流侧纹波的目的。但直流偏置系数不能太大，且要满足Ud1+Ud2=Ud。该解耦方式前提是直流分裂电容值相等，但本文主要侧重于研究存在电容偏差下的APD控制技术，因此不深入讨论。
针对提出的3种解耦方式进行参数设计和控制策略研究。假设两直流分裂电容值不相等，且$ {C_1} = m{C_2} $，m为分裂电容不匹配系数。且假设2个分裂电容的直流电压Ud1和Ud2满足
$$ \left\{ \begin{gathered} {U_{{\mathrm{d}}1}} = (1 - n){U_{\mathrm{d}}} \\ {U_{{\mathrm{d}}2}} = n{U_{\mathrm{d}}} \\ \end{gathered} \right. $$ (8) 式中n为直流偏置系数。
Ud1和Ud2应大于0且小于Ud，同时满足Ud1+Ud2=Ud，因此n满足0≤n≤1。
二次电压幅值为
$$ {U_{\mathrm{c}}} = \frac{{\sqrt {{{(UI)}^2} + 2\omega {L_2}U{I^3}\sin \varphi + {{(\omega {L_2}{I^2})}^2}} }}{{4N\omega {C_2}{U_{\mathrm{d}}}\left| {m(1 - n) - n} \right|}} $$ (9) 通过分析参数m和n对Uc的影响，选取合适的取值进一步缩小电容值，减小矿用电力电子设备的体积。由于Ud2+Uc<Ud调制条件的约束，结合式（8）和式（9）可得Uc的最大值Uc.max=Ud/2。若其他参数恒定，当直流分裂电容的二次电压幅值为最大值时，解耦电容值最小。其取值范围为
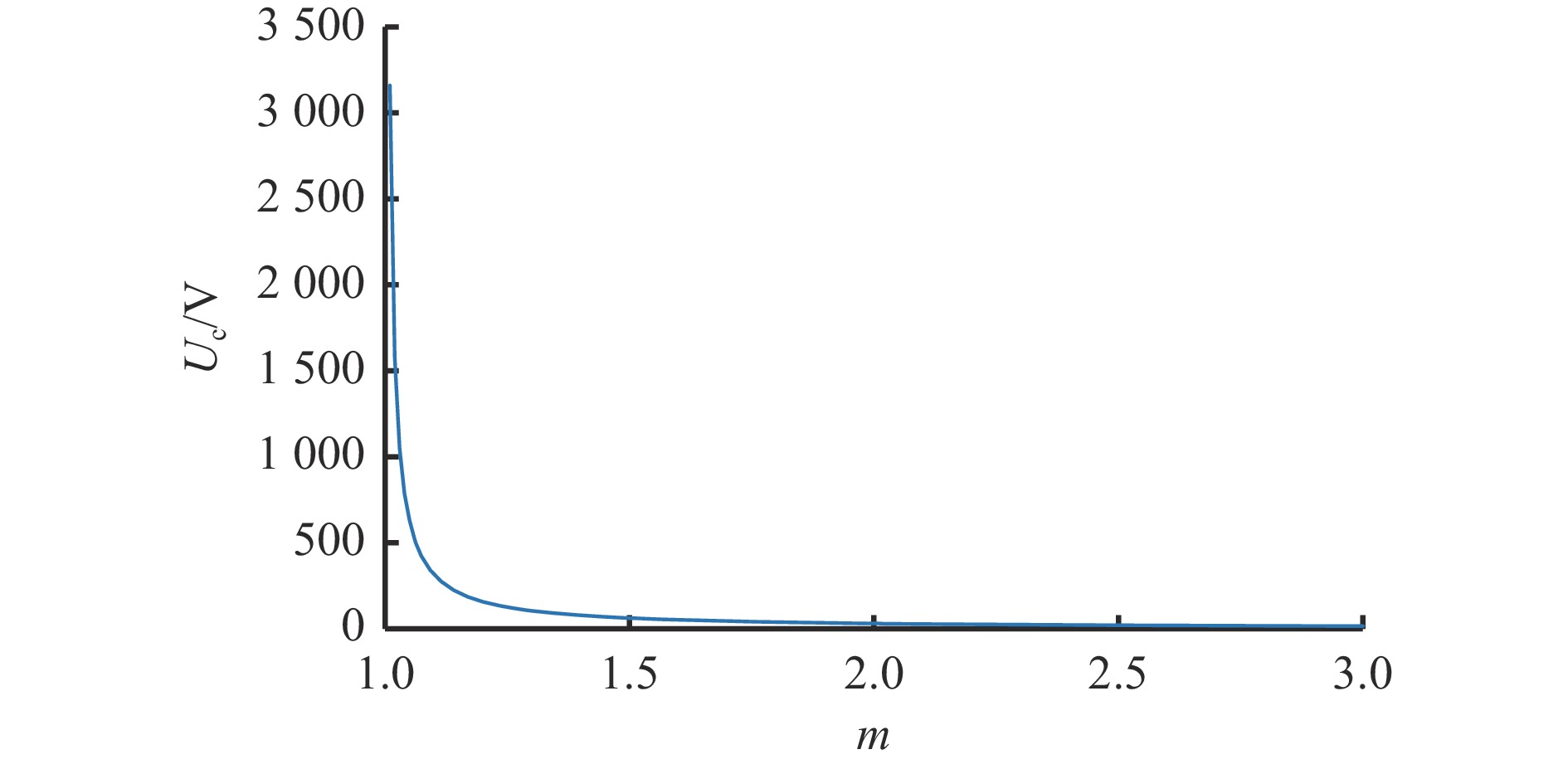
$$ {C_2} \geqslant \frac{{UI}}{{2\omega {U_{\mathrm{d}}^2}\left| {m - 1} \right|}} $$ (10) 为分析不匹配系数m对二次电压幅值Uc的影响，设直流偏置系数n=0.5，2个分裂电容的直流电压分量相等，即Ud1=Ud2=Ud/2，忽略滤波电感损耗，根据式（9）得到m与Uc之间的关系曲线，如图2所示。可看出随着m增大，Uc急剧下降。因此可通过选取适当的m来减小电容值。
![]()
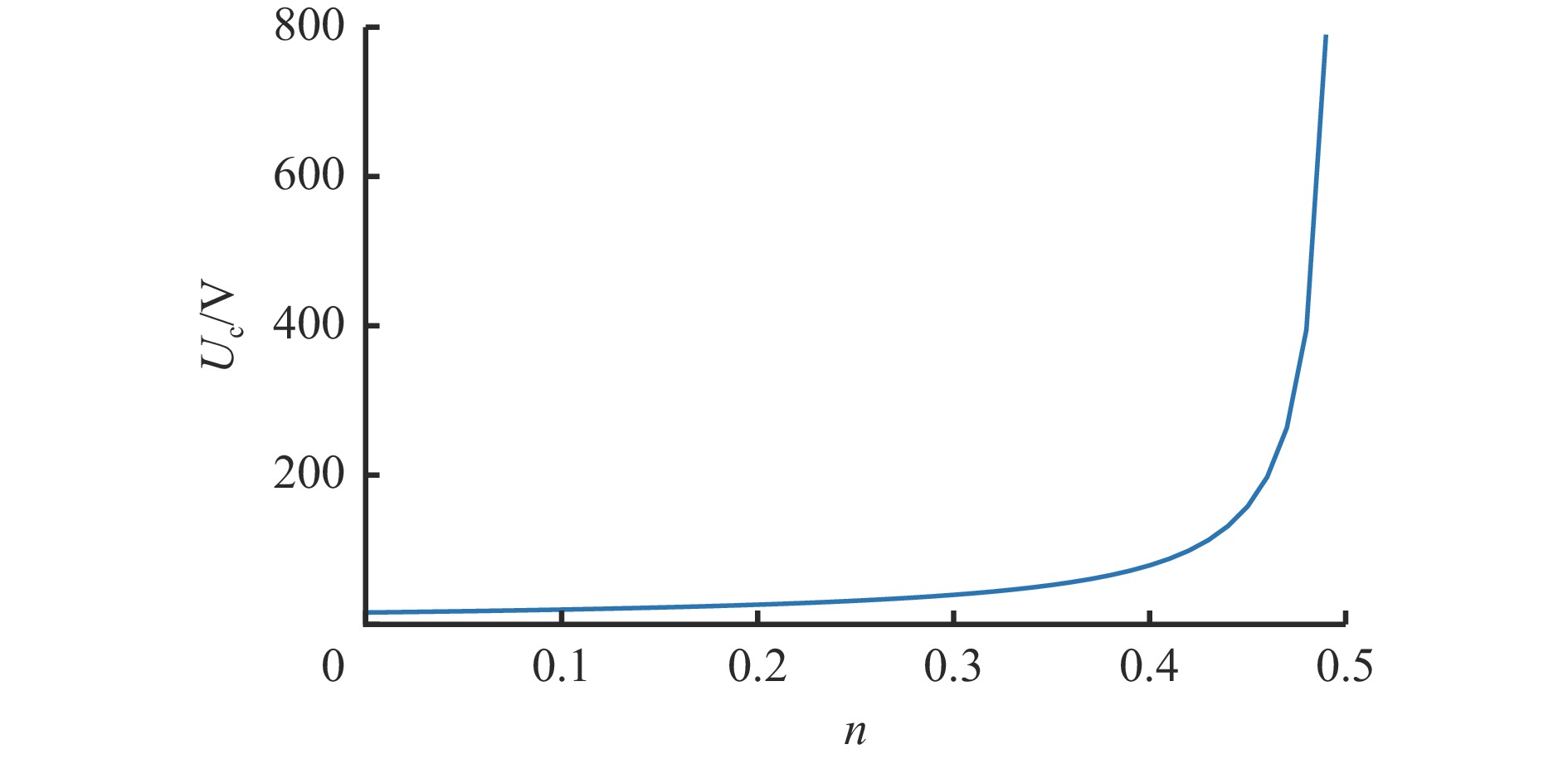
图 2 二次电压幅值Uc与不匹配系数m之间的关系Figure 2. Relationship between the double frequency voltage amplitude Uc and the mismatch coefficient m为分析直流偏置系数n对二次电压幅值Uc的影响，设不匹配系数m=1，得到n与Uc之间的关系曲线，如图3所示。可看出随着n增大，Uc增大，n>0.4时Uc急剧上升，n=0.5时Uc接近无穷大。Uc会导致对称半桥电路上的电流应力上升，不利于减小电容值，因此n应尽量小。从上述分析可得，Uc受到m和n 2个因素的影响，而m与电容的真实状态相关，因此，在设计功率解耦控制器之前，应确定n的最优选择范围。
![]()
图 3 二次电压幅值Uc与直流偏置系数n之间的关系Figure 3. Relationship between the double frequency voltage amplitude Uc and the DC bias coefficient n以n<0.5为例进行分析。由式（8）可知Ud1>Ud2，为使电路安全运行，C1电压最大值Uc1.max和C2电压最小值Uc2.min应满足：
$$ \left\{ \begin{gathered} {U_{{\mathrm{c}}1.\max }} = {U_{{\mathrm{d}}1}} + {U_{\mathrm{c}}} < {U_{\mathrm{d}}} \\ {U_{{\mathrm{c}}2.\min }} = {U_{{\mathrm{d}}2}} - {U_{\mathrm{c}}} > 0 \\ \end{gathered} \right. $$ (11) 将式（8）代入式（11），可得直流偏置系数n的约束不等式：
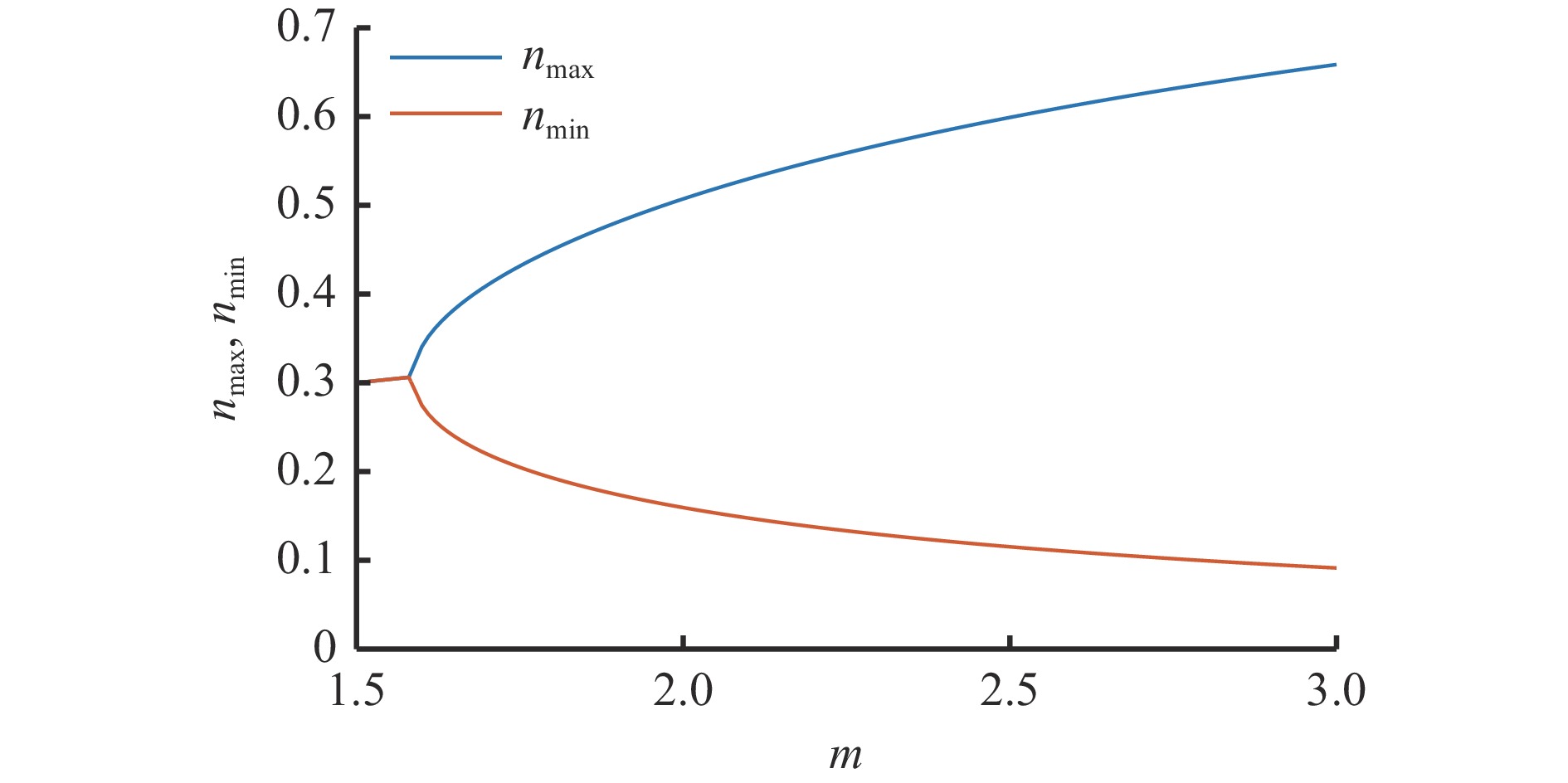
$$ n{U_{\mathrm{d}}} - {U_{\mathrm{c}}} > 0 $$ (12) 忽略交流侧电感的影响，可得直流偏置系数n的最大值nmax和最小值nmin与不匹配系数m的关系表达式：
$$ \left\{ \begin{array}{l} \mathop n\nolimits_{\max } = \dfrac{{m\omega {C_2}{U_{\rm{d}}} + \sqrt {{{(m\omega {C_2}{U_{\rm{d}}})}^2} - \omega {C_2}UI(m + 1)} }}{{2\omega {C_2}{U_{\rm{d}}}(m + 1)}}\\ {n_{\min }} = \dfrac{{m\omega {C_2}{U_{\rm{d}}} - \sqrt {{{(m\omega {C_2}{H})}^2} - \omega {C_2}UI(m + 1)} }}{{2\omega {C_2}{U_{\rm{d}}}(m + 1)}} \end{array} \right. $$ (13) nmax和nmin随m变化曲线如图4所示。可看出随着m从1.6增大到3，n的取值范围越来越大，越来越灵活。为保证系统在整个m变化范围内正常工作，通常取n为nmax和nmin的平均值，即n=0.32。
![]()
图 4 直流偏置系数最大值nmax、最小值nmin与不匹配系数m之间的关系Figure 4. Relationship between the maximum value nmax of DC bias coefficient, the minimum value nmin and the mismatch coefficient m2个分裂电容电压的最大值与直流偏置系数n的关系为
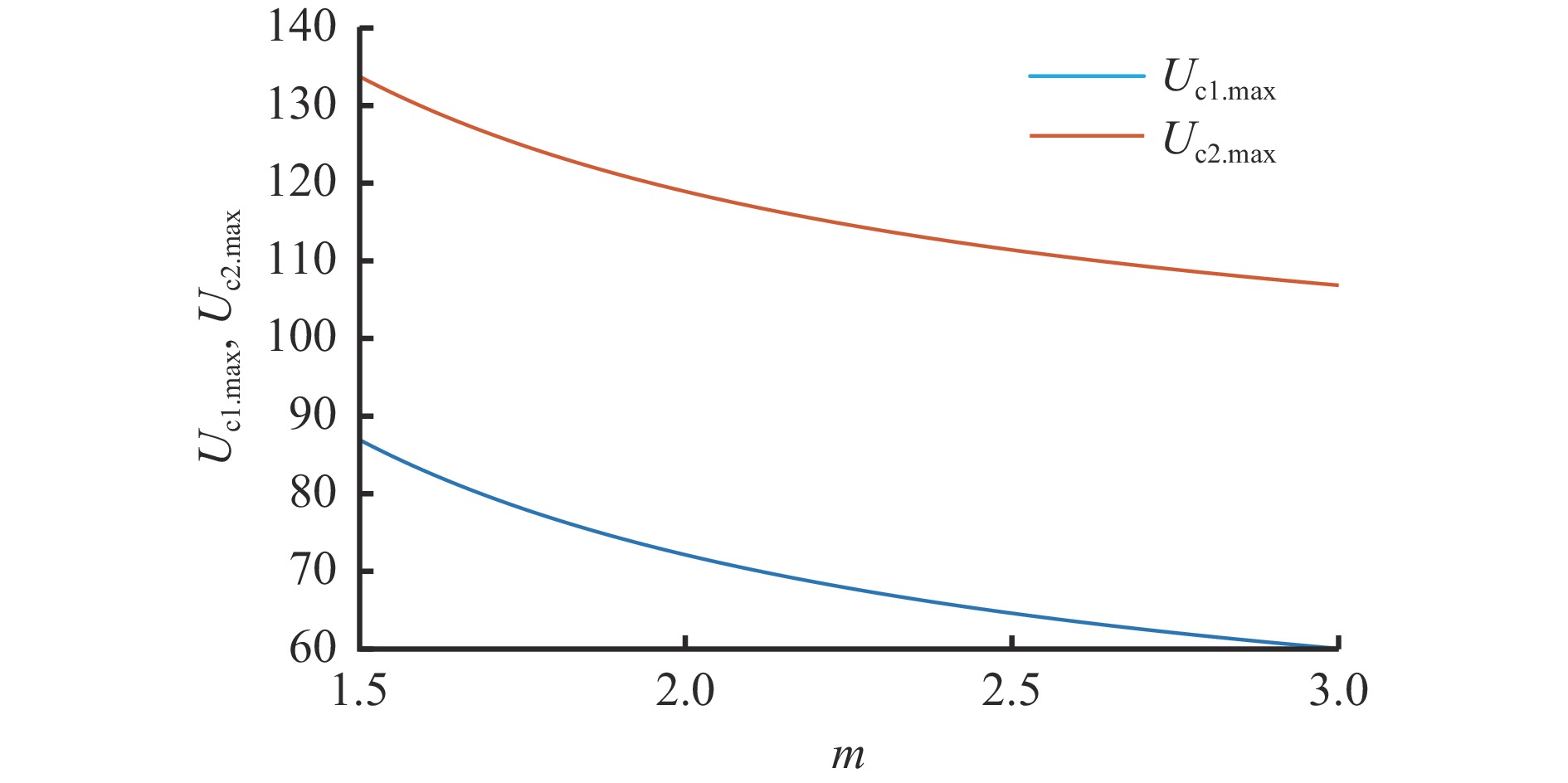
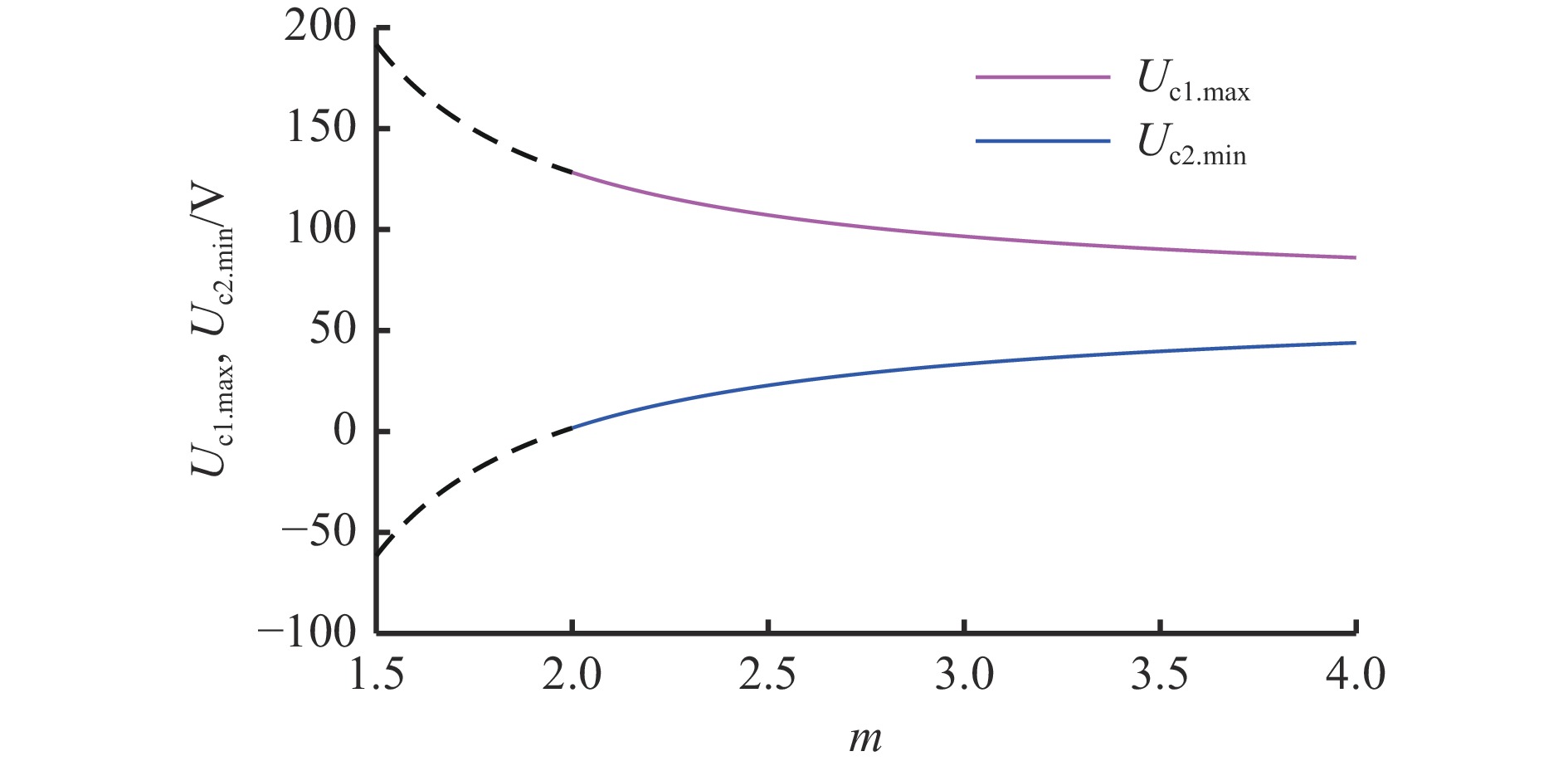
$$ \left\{ \begin{gathered} {U_{{\mathrm{c}}1.\max }} = (1 - n){U_{\mathrm{d}}} + {U_{\mathrm{c}}} \\ {U_{{\mathrm{c}}2.\max }} = n{U_{\mathrm{d}}} + {U_{\mathrm{c}}} \\ \end{gathered} \right. $$ (14) 将n=0.32代入式（14），结合式（9），可得2个分裂电容电压最大值与不匹配系数m的关系曲线，如图5所示。可看出Uc1.max始终大于Uc2.max，并随着m增大同比衰减。当n=0.32时，保持分裂电容C2合适的低电压，有利于降低所需的电容值。此时m=2.5。
![]()
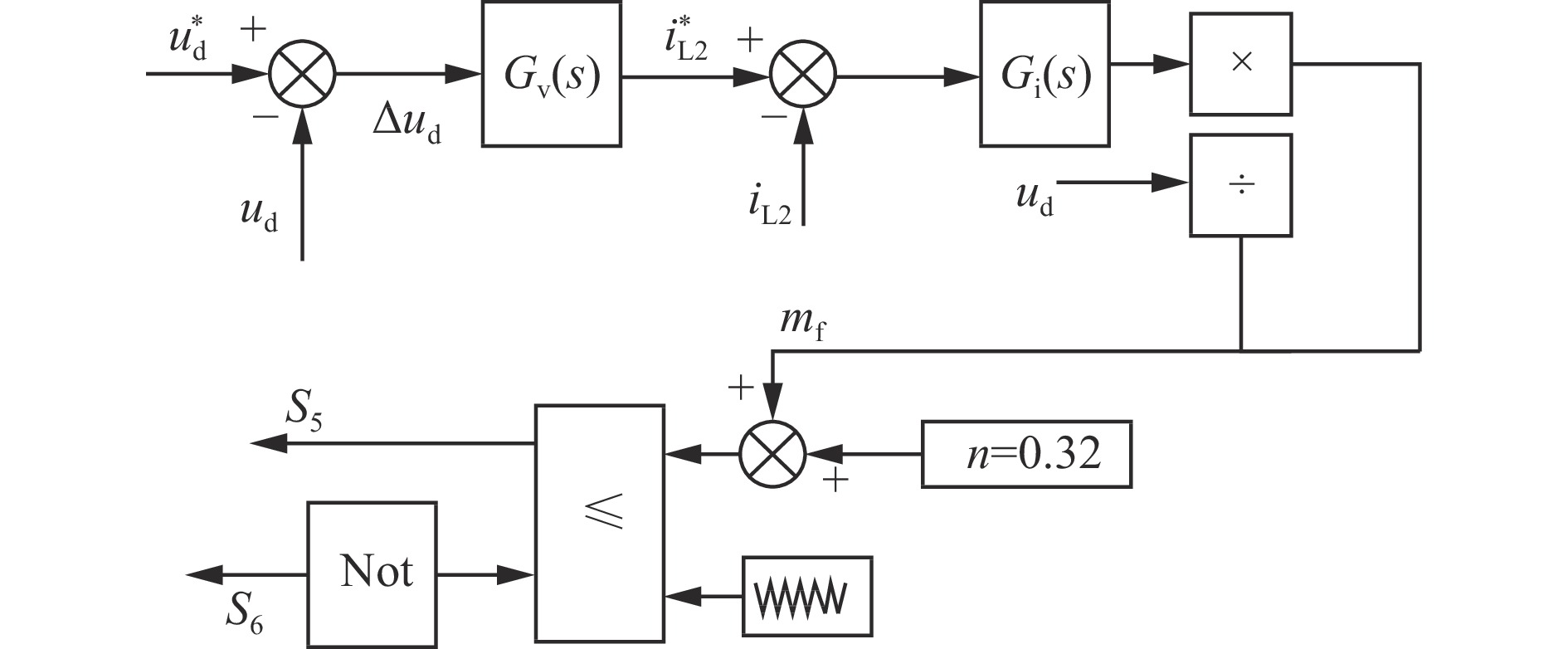
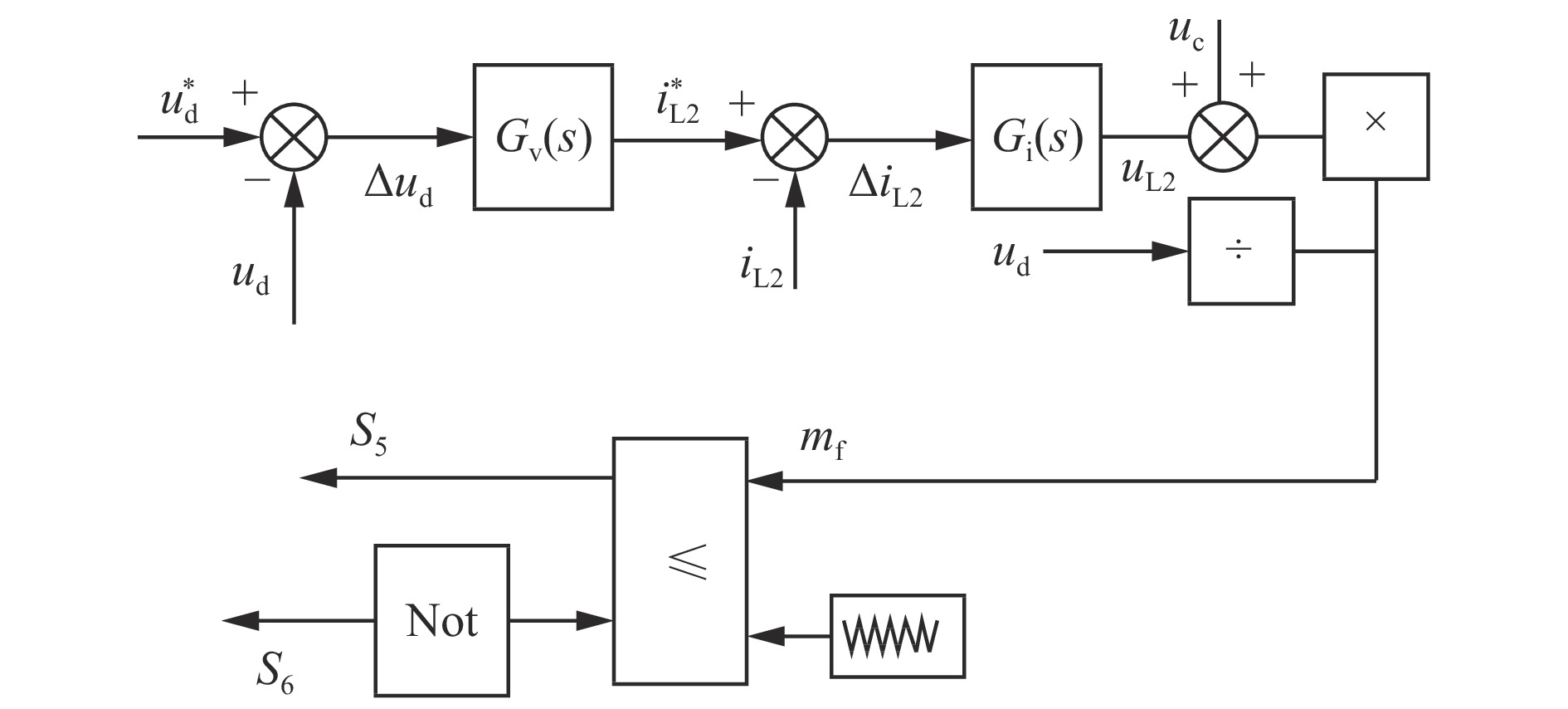
图 5 2个分裂电容最大值Uc1.max，Uc2.max与不匹配系数m之间的关系Figure 5. Relationship between the maximum value Uc1.max，Uc2.max of two split capacitances and the mismatch coefficient m1） 基于解耦方式2的2种控制方法。直接给定直流偏置系数n的SC−IAPD电路控制方法原理如图6所示。其中$u_{\mathrm{d}}^*$为参考直流电压；${u_{\mathrm{d}}}$为实际直流电压；$\Delta {u_{\mathrm{d}}}$为参考直流电压与实际直流电压的差值；${G_{\mathrm{v}}}\left( s \right)$为电压环传递函数，s为拉普拉斯算子；$i_{{\mathrm{L}}2}^*$为解耦电感电流参考值；${G_{\mathrm{i}}}\left( s \right)$为电流环传递函数；S5，S6为开关信号，mf为选定的分裂电容不匹配系数。
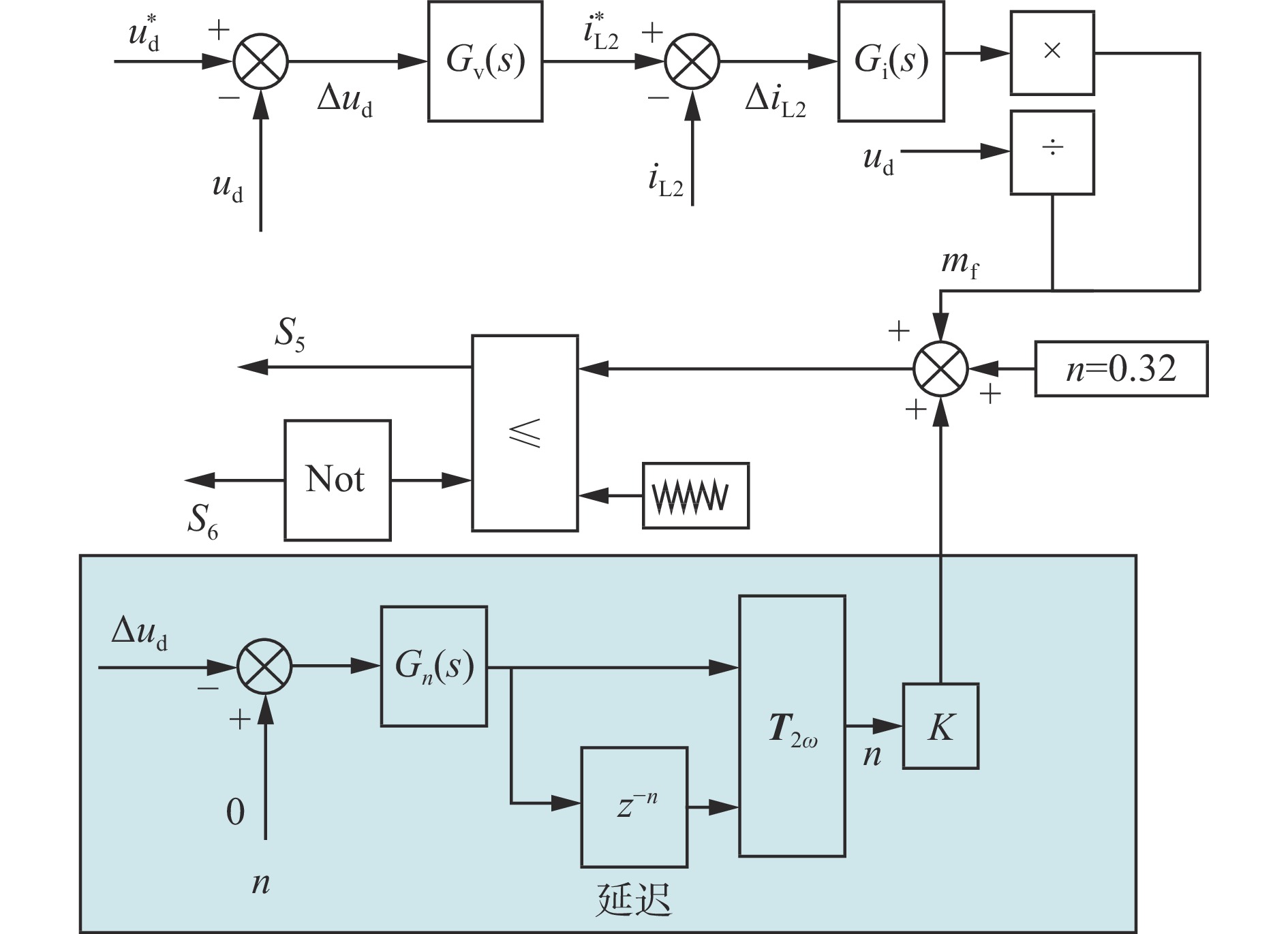
为了抑制负载变化时直流侧的电压纹波，直流偏置系数n也会发生变化。针对该种直接给定直流偏置系数进行构造二次电压的控制方法不够灵活、鲁棒性较差的缺点，本文研究了一种优化控制方法，通过对二次电压波动进行控制，可得跟随负载变化的n参考值。SC−IAPD电路的优化控制方法原理如图7所示。其中${G_n}(s)$为比例谐振控制器（Proportional Resonance Controller,PR）控制器；${{\boldsymbol{T}}_{2\omega }}$为角频率为2ω的旋转矩阵；K为变换系数；z-n为延迟。
![]()
图 7 SC−IAPD电路的优化控制方法原理Figure 7. Principle of the optimized SC-IAPD circuit control method$$ G_{\mathrm{n}}\left(s\right)=K_{\mathrm{p}}+\frac{K_{\mathrm{r}}s}{s^2+(2\omega)^2} $$ (15) $$ {{\boldsymbol{T}}_{2\omega }} = \left[ \begin{gathered} \cos \;2\omega t \\ - \sin\; 2\omega t \\ \end{gathered} \right.{\text{ }}\left. \begin{gathered} \sin\; 2\omega t \\ \cos\; 2\omega t \\ \end{gathered} \right] $$ (16) 式中：$ {K_{\mathrm{p}}} $为比例系数；$ {K_{\mathrm{r}}} $为谐振点处增益。
2） 基于解耦方式1的控制方法。设n=0.5，即Ud1=Ud2=Ud/2，仅使分裂电容值不等，即合理设计不匹配系数m，使电路产生的二次纹波功率来补偿交流侧的二次脉动功率，达到消除SCHBR直流侧二次电压纹波的目的。
2个分裂电容满足$ C_{1}=mC_{2} $。设C1＞C2，则m>1，为保证电路的安全运行，C1电压最大值Uc1.max和C2电压最小值Uc2.min应满足下式，且满足m>2。
$$ \left\{ \begin{gathered} {U_{{\mathrm{c}}1.\max }} = \frac{1}{2}{U_{\mathrm{d}}} + {U_{\mathrm{c}}} < {U_{\mathrm{d}}} \\ {U_{{\mathrm{c}}2.\min }} = \frac{1}{2}{U_{{\mathrm{d}}}} - {U_{\mathrm{c}}} > 0 \\ \end{gathered} \right. $$ (17) 结合式（9），可得Uc1.max和Uc2.min与$ m $的关系，如图8所示。可看出Uc1.max与Uc2.min关于Ud/2对称，并随$ m $增大而衰减，逐渐逼近对称轴。
![]()
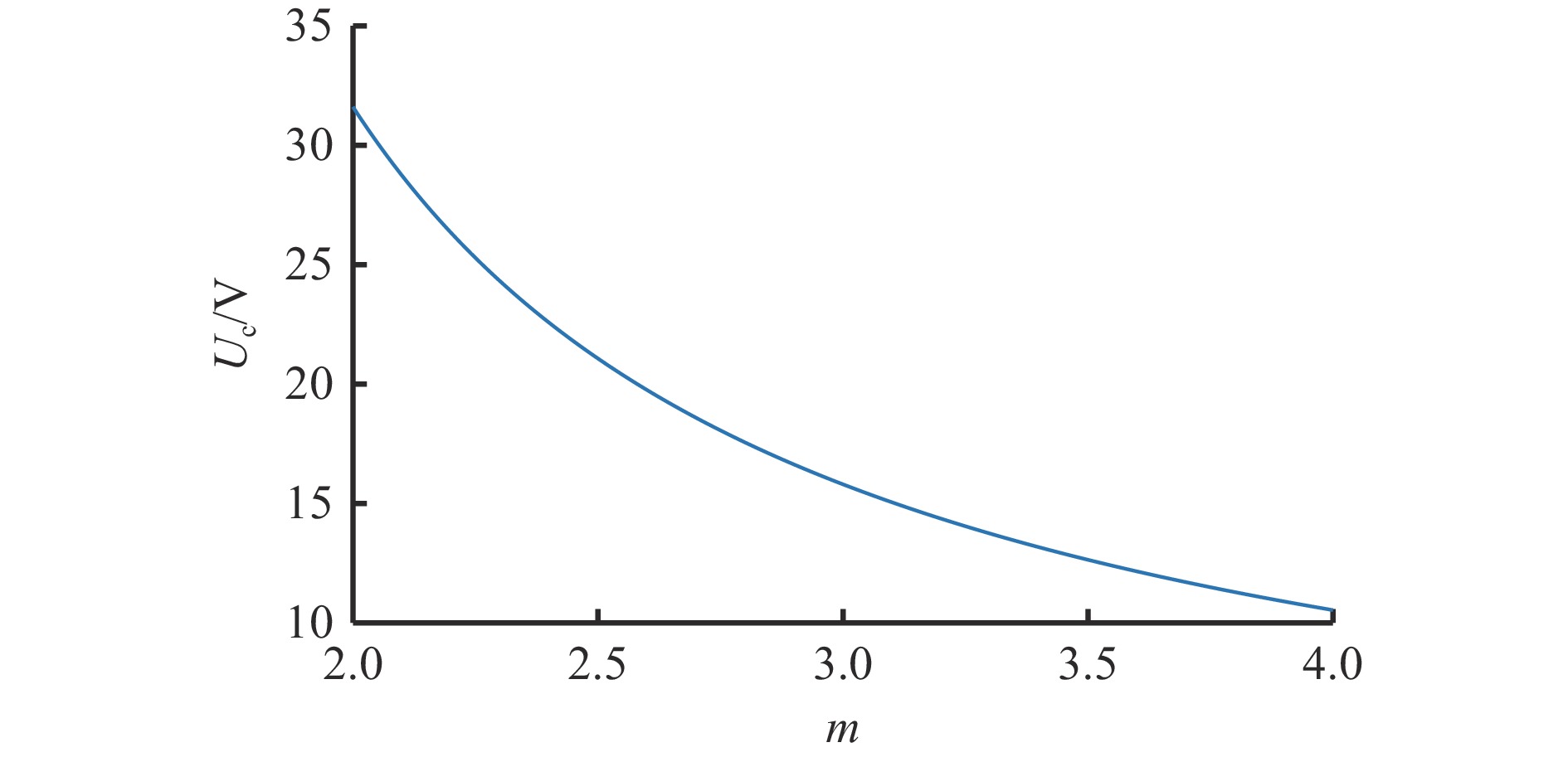
图 8 Uc1.max，Uc2.min与m之间的关系Figure 8. Relationship between Uc1.max, Uc2.min and the mismatch coefficient m基于解耦方式1的 SC−IAPD电路控制方法不对直流偏置系数n进行控制，即Ud1=Ud2=Ud/2，n=0.5。将SCHBR参数（表1）代入式（9）可得二次电压幅值${U_{\mathrm{c}}}$随不匹配系数$ m $的变化趋势，如图9所示。可看出要保持分裂电容较低的$ {U_{\mathrm{c}}} $，当较小电容值不变时，有利于降低较大电容值，节约功率解耦成本。因此m=3.5，若C2=300 μF，则C1=mC2=1.05 mF。此时Uc≈13 V，符合设计要求。
表 1 基于SC−IAPD的SCHBR参数Table 1. Parameters of SCHBR based on SC-IAPD参数 值 参数 值 H桥开关频率/kHz 10 装置容量/kW 10 电网频率/Hz 50 级联单元数/个 2 电网电压幅值/V 155 直流侧电容/mF 1.5 并网电感/mH 0.8 直流侧输出电压/V 130 解耦电感/mH 4 分裂电容/mF C1=0.75，C2=0.3 ![]()
图 9 基于解耦方式1时，二次电压幅值Uc与不匹配系数m之间的关系Figure 9. Relationship between the double frequency voltage amplitude Uc and the mismatch coefficient m based on decoupling model 1基于解耦方式1的 SC−IAPD电路控制方法原理如图10所示。该控制方法中解耦电感电流的给定值是由PR控制器直接从直流电压纹波中提取的，无需经过延时降频环节，可获得更快的响应。该控制下2个分裂电容中较大电容值小于传统控制方法，减小了矿用电力电子设备的体积和成本。
![]()
图 10 基于解耦方式1的 SC−IAPD电路控制方法原理Figure 10. Principle of the SC-IAPD circuit control method based on decoupling mode 14. 基于构造二次电压解耦控制仿真和实验分析
4.1 仿真分析
为了验证3种控制方法在不同煤矿应用场景下的优势，在Matlab/Simulink中搭建相关仿真模型，仿真参数见表1。
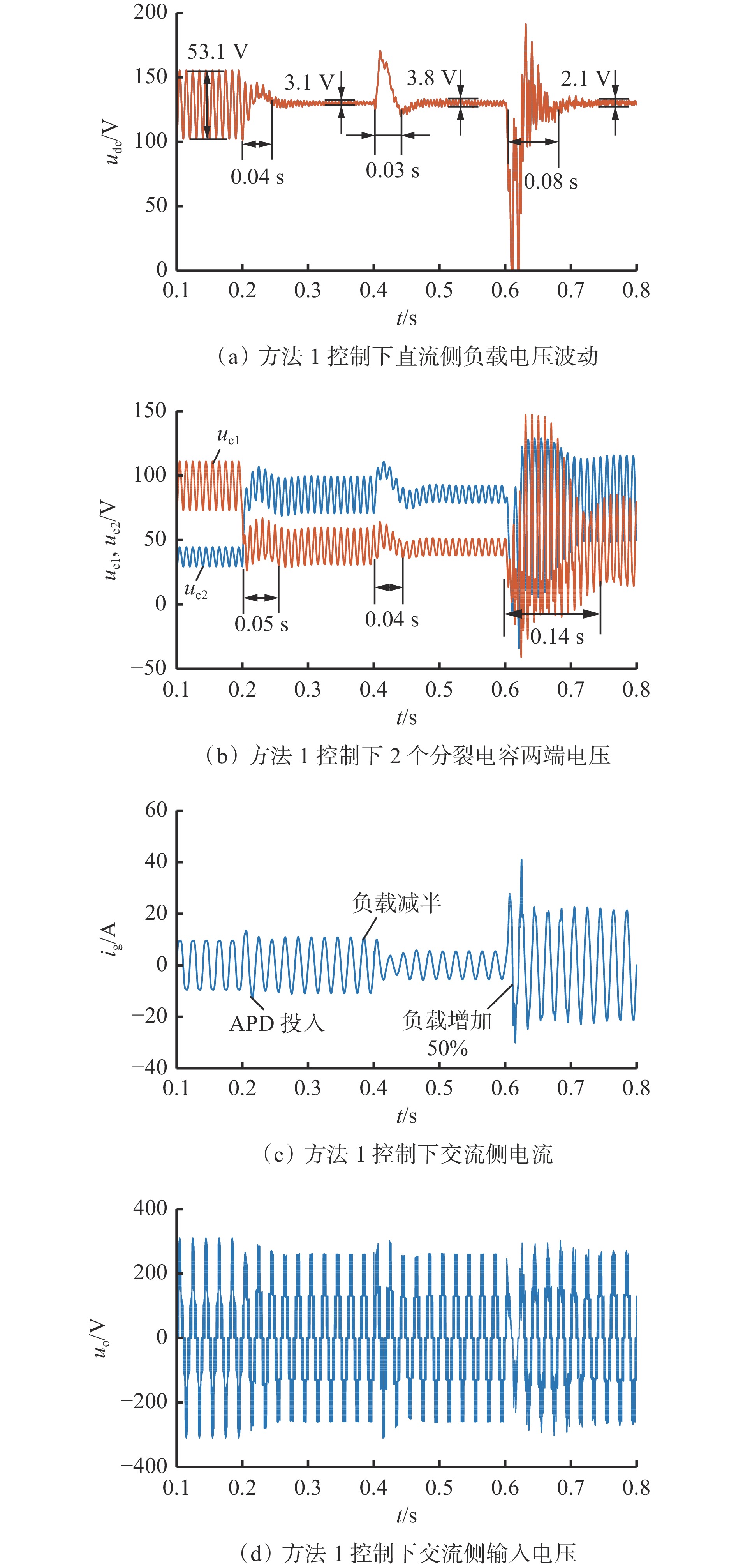
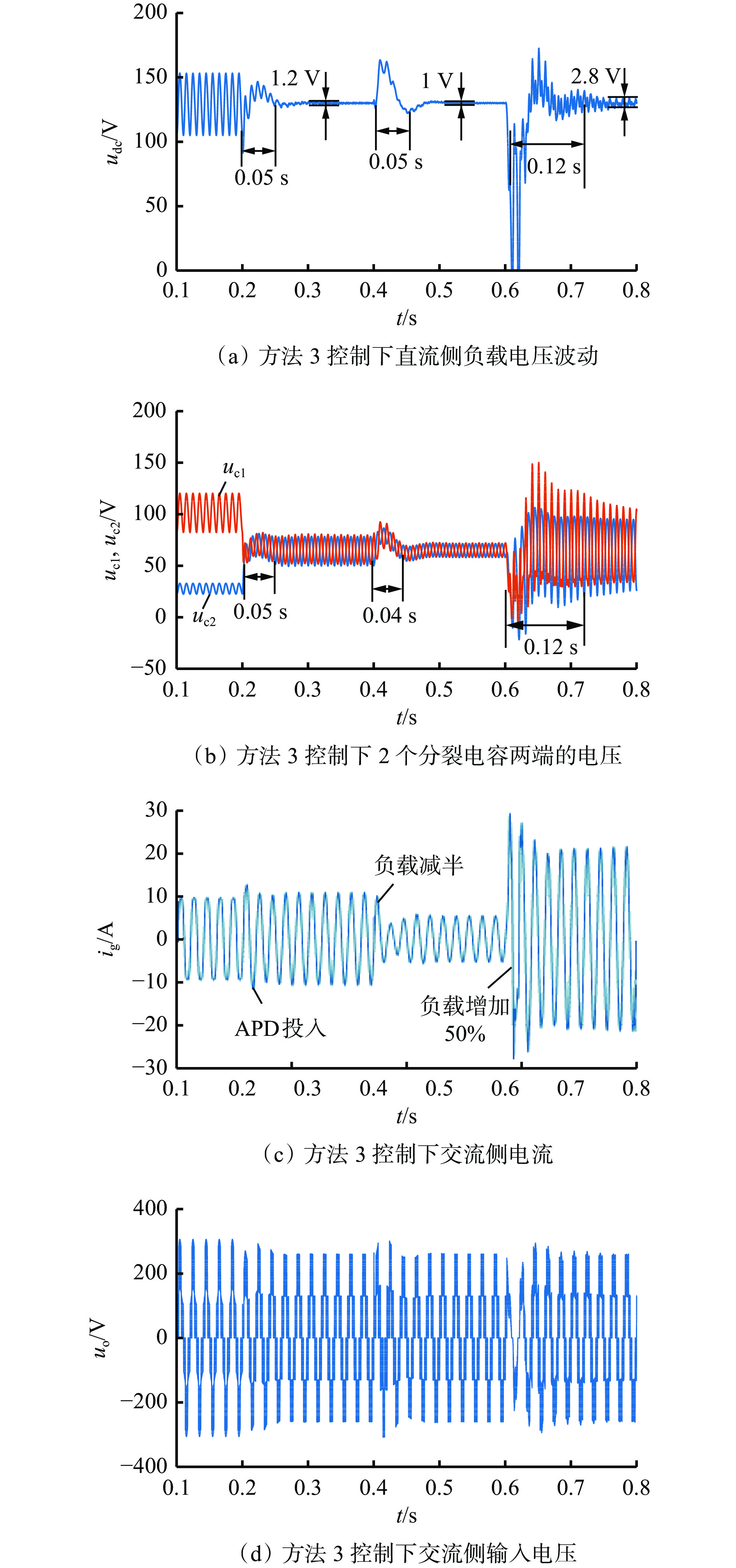
针对3种基于构造二次电压解耦的控制方法，系统从切入APD控制到负载减半再到重载的相关输出波形如图11−图13所示，其中udc为直流侧电压，ig为交流侧电流，uo为H桥输入电压。
![]()
图 11 改变负载时方法1控制下的基于SC−IAPD的SCHBR仿真波形Figure 11. SCHBR simulation waveform based on SC-IAPD under the method 1 control when changing load![]()
图 12 改变负载时方法2控制下的基于SC−IAPD的SCHBR仿真波形Figure 12. SCHBR simulation wavefor based on SC-IAPD under the method 2 control when changing load![]()
图 13 改变负载时方法3控制下的基于SC−IAPD的SCHBR仿真波形Figure 13. SCHBR simulation waveform based on SC-IAPD under the method 3 control when changing load由图11−图13可看出，在0.2 s时加入SC−IAPD电路，3种方法的直流侧输出电压纹波都控制在1.0～1.5 V左右，说明对称半桥解耦电路可有效抑制直流电压波动，同时在负荷变化时具有良好的解耦性能。在0.4 s时将负载减小50%，图11 （a）中的电压波动为0.7 V，图12（a）中的电压波动为1.1 V，图13（a）中的电压波动为0.2 V，可看出方法2中直流偏置系数跟随负载变化的解耦控制的纹波抑制效果不如其他2种控制方法。当负载在0.6 s增加50%时，图11（a）中系统经过0.14 s达到稳态，电压纹波为2.1 V，图13（a）中系统经过0.12 s达到稳态，电压纹波为2.8 V，这2种方法的解耦效果近似，而图12（a）中系统经过0.08 s达到稳态，电压纹波仅为2.1 V，纹波与直流电压比值小于3%，符合MT/T 863—2000《矿用直流电源变换器》要求。
可见，在轻载切重载的情况下，方法2能快速跟随负载变化，实现纹波抑制，具有更强的带载能力和更佳的解耦效果。而在重载切轻载的情况下，直接给定偏置系数或只通过使分裂电容值不等的控制方法能够更好地实现解耦性能，将电压纹波控制在1 V以内。如果考虑电容值的最小化，控制方法1则更具优势。
4.2 实验验证
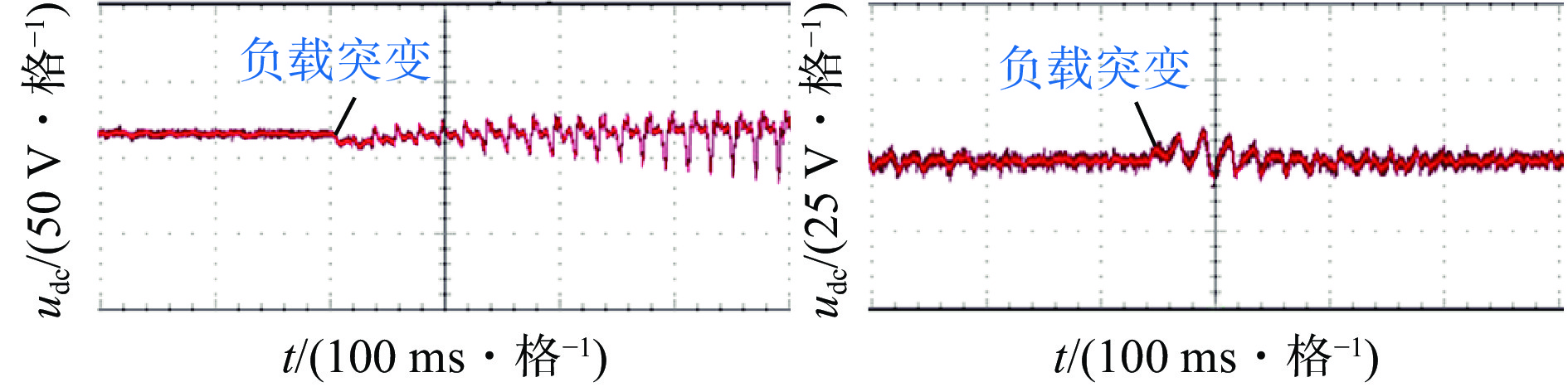
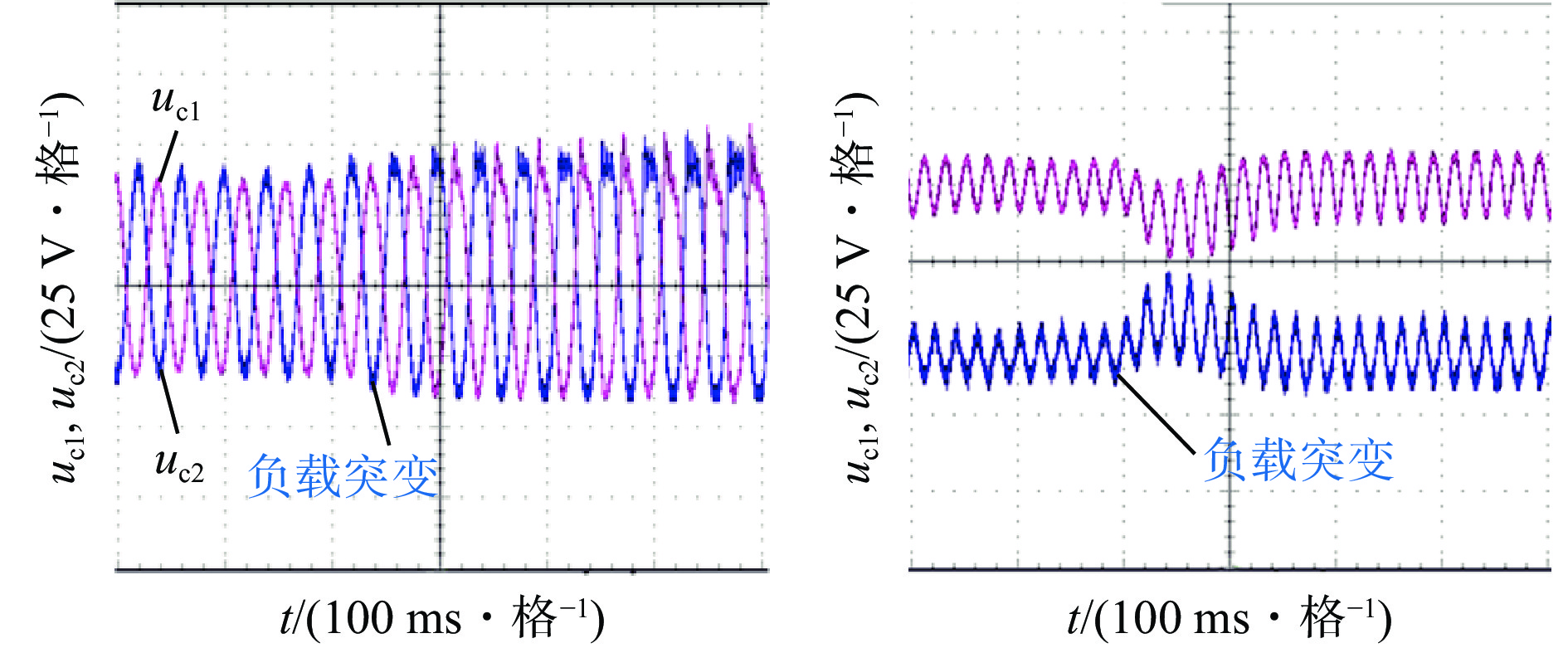
为验证所提控制方法的有效性，以煤矿应急储能系统的级联H桥拓扑结构为例，利用硬件在RT−LAB半实物仿真平台搭建模型，硬件参数与仿真参数一致。根据上述仿真结果，选择方法2进行实验。传统控制与本文控制方法下的直流输出电压、分裂电容电压实验波形分别如图14、图15所示。
![]()
图 14 传统控制与本文控制方法下的直流输出电压实验波形Figure 14. Experimental waveform of DC output voltage under traditional control and the control method in the paper由图14和图15可看出，在负载突变前，传统控制方法和本文控制方法都能对直流侧的电压纹波进行抑制，但本文控制方法的解耦效果更佳，直流侧的电压纹波更小。在负载突变后，传统控制方法控制下的直流侧电压${u_{{\mathrm{dc}}}}$开始出现较大的震荡，失去稳定；本文控制方法控制下的${u_{{\mathrm{dc}}}}$经过一个小的震荡迅速达到稳定状态，且能有效抑制直流侧电压纹波。这说明基于二次电压的解耦控制方法所需的解耦电容值更小，具有更优的动态性能，且带载能力更强，当负载增大时，仍保持良好的功率解耦性能。
![]()
图 15 传统控制与本文控制方法下的分裂电容电压实验波形Figure 15. Experimental waveform of split capacitance voltage under traditional control and the control methods in the paper5. 结论
1） 基于构造二次电压的解耦控制方法能够有效避免电容不匹配时直流侧产生的基频功率脉动问题，并实现对直流侧电压二次纹波的有效抑制，能够在不同的工作条件下保持稳定的解耦性能，确保电力电子变换器的可靠性和效率。
2） 通过采用基于构造二次电压的解耦控制方法，要保持分裂电容较低的二次电压幅值，当较小容值电容不变时，有利于降低较大电容值，从而减小矿用电力电子设备的体积和成本。
3） 基于构造二次电压的解耦原理，设计了3种不同的解耦控制方法，并优化了控制参数。仿真结果表明，在0.2 s时加入SC−IAPD电路，3种方法的直流侧输出电压纹波都控制在1.0～1.5 V左右，说明对称半桥解耦电路可有效抑制直流电压波动，同时在负荷变化时具有良好的解耦性能。可根据不同的应用场景选择合适的控制策略。
4） 在MATLAB仿真和RT−LAB半仿真平台验证了所提方法的可行性和有效性。基于二次电压的解耦控制方法下所需的解耦电容值更小，具有更优的动态性能，且带载能力更强，当负载增大时仍保持良好的功率解耦性能。
-
![]()
图 1 基于SC−IAPD的矿用SCHBR主电路拓扑
Figure 1. Main circuit topology of mine single-phase cascaded H bridge rectifier（SCHBR） based on split capacitor IAPD （SC-IAPD）
![]()
图 2 二次电压幅值Uc与不匹配系数m之间的关系
Figure 2. Relationship between the double frequency voltage amplitude Uc and the mismatch coefficient m
![]()
图 3 二次电压幅值Uc与直流偏置系数n之间的关系
Figure 3. Relationship between the double frequency voltage amplitude Uc and the DC bias coefficient n
![]()
图 4 直流偏置系数最大值nmax、最小值nmin与不匹配系数m之间的关系
Figure 4. Relationship between the maximum value nmax of DC bias coefficient, the minimum value nmin and the mismatch coefficient m
![]()
图 5 2个分裂电容最大值Uc1.max，Uc2.max与不匹配系数m之间的关系
Figure 5. Relationship between the maximum value Uc1.max，Uc2.max of two split capacitances and the mismatch coefficient m
![]()
图 7 SC−IAPD电路的优化控制方法原理
Figure 7. Principle of the optimized SC-IAPD circuit control method
![]()
图 8 Uc1.max，Uc2.min与m之间的关系
Figure 8. Relationship between Uc1.max, Uc2.min and the mismatch coefficient m
![]()
图 9 基于解耦方式1时，二次电压幅值Uc与不匹配系数m之间的关系
Figure 9. Relationship between the double frequency voltage amplitude Uc and the mismatch coefficient m based on decoupling model 1
![]()
图 10 基于解耦方式1的 SC−IAPD电路控制方法原理
Figure 10. Principle of the SC-IAPD circuit control method based on decoupling mode 1
![]()
图 11 改变负载时方法1控制下的基于SC−IAPD的SCHBR仿真波形
Figure 11. SCHBR simulation waveform based on SC-IAPD under the method 1 control when changing load
![]()
图 12 改变负载时方法2控制下的基于SC−IAPD的SCHBR仿真波形
Figure 12. SCHBR simulation wavefor based on SC-IAPD under the method 2 control when changing load
![]()
图 13 改变负载时方法3控制下的基于SC−IAPD的SCHBR仿真波形
Figure 13. SCHBR simulation waveform based on SC-IAPD under the method 3 control when changing load
![]()
图 14 传统控制与本文控制方法下的直流输出电压实验波形
Figure 14. Experimental waveform of DC output voltage under traditional control and the control method in the paper
![]()
图 15 传统控制与本文控制方法下的分裂电容电压实验波形
Figure 15. Experimental waveform of split capacitance voltage under traditional control and the control methods in the paper
表 1 基于SC−IAPD的SCHBR参数
Table 1 Parameters of SCHBR based on SC-IAPD
参数 值 参数 值 H桥开关频率/kHz 10 装置容量/kW 10 电网频率/Hz 50 级联单元数/个 2 电网电压幅值/V 155 直流侧电容/mF 1.5 并网电感/mH 0.8 直流侧输出电压/V 130 解耦电感/mH 4 分裂电容/mF C1=0.75，C2=0.3 
下载: 导出CSV
-
[1] 张传金,李雨潭,刘战,等. 矿用LCL型三电平静止无功发生器控制策略[J]. 工矿自动化,2020,46(5):87-93. ZHANG Chuanjin,LI Yutan,LIU Zhan,et al. Control strategy of mine-used LCL three-level static var generator[J]. Industry and Mine Automation,2020,46(5):87-93.
[2] 田旭,马越. 矿井链式静止同步补偿器电流跟踪控制策略[J]. 工矿自动化,2019,45(4):49-53,82. TIAN Xu,MA Yue. Current tracking control strategy for mine chain STATCOM[J]. Industry and Mine Automation,2019,45(4):49-53,82.
[3] 王国法,王虹,任怀伟,等. 智慧煤矿2025情景目标和发展路径[J]. 煤炭学报,2018,43(2):295-305. WANG Guofa,WANG Hong,REN Huaiwei,et al. 2025 scenarios and development path of intelligent coal mine[J]. Journal of China Coal Society,2018,43(2):295-305.
[4] 李悦. 九部门联合印发“十四五”可再生能源发展规划[N]. 中国气象报,2022-06-08(第1版). LI Yue. Nine departments jointly issued the 14th Five-Year Plan for renewable energy development[N]. China Meteorological News,2022-06-08(1th ed).
[5] 梅家棋,赵一潇,程晋培,等. 混合级联桥式整流电路与级联多电平整流电路应用研究[J]. 煤炭工程,2021,53(12):125-130. MEI Jiaqi,ZHAO Yixiao,CHENG Jinpei,et al. Application of hybrid cascade bridge rectifier circuit and cascade multilevel rectifier circuit[J]. Coal Engineering,2021,53(12):125-130.
[6] 李定甲,苏玉香,刘安国,等. 矿用级联多电平变换器输出谐波特性研究[J]. 煤矿机械,2023,44(10):37-39. LI Dingjia,SU Yuxiang,LIU Anguo,et al. Research on output harmonic characteristics of mining cascade multilevel converter[J]. Coal Mine Machinery,2023,44(10):37-39.
[7] 李定甲,苏玉香,刘安国,等. 级联多电平有源电力滤波器在煤矿电网谐波补偿中的应用研究[J]. 煤矿机械,2023,44(8):154-156. LI Dingjia,SU Yuxiang,LIU Anguo,et al. Research on application of cascaded multi-level active power filter on harmonic compensation of coal mine power grid[J]. Coal Mine Machinery,2023,44(8):154-156.
[8] 陶海军,肖群星,张金生,等. 单相级联型多电平变换器直流纹波电压分析及抑制策略[J]. 河南理工大学学报(自然科学版),2024,43(1):113-123. TAO Haijun,XIAO Qunxing,ZHANG Jinsheng,et al. Analysis and suppression strategy of DC ripple voltage of single-phase cascaded multilevel converter[J]. Journal of Henan Polytechnic University(Natural Science),2024,43(1):113-123.
[9] 贺虎成,谭阜琛,司堂堂,等. 基于SVG的采煤机电能质量控制策略研究[J]. 煤炭工程,2022,54(8):129-135. HE Hucheng,TAN Fuchen,SI Tangtang,et al. Control strategy of electric power quality governance of coal shearer based on SVG[J]. Coal Engineering,2022,54(8):129-135.
[10] 叶满园,康力璇. 单相级联H桥光伏并网逆变器功率平衡控制策略研究[J]. 电源学报,2020,18(4):137-143. YE Manyuan,KANG Lixuan. Research on power balance control strategy for single-phase cascaded H-bridge photovoltaic grid-connected inverter[J]. Journal of Power Supply,2020,18(4):137-143.
[11] SAJADI R,IMAN-EINI H,BAKHSHIZADEH M K,et al. Selective harmonic elimination technique with control of capacitive DC link voltages in an asymmetric cascaded H-bridge inverter for STATCOM application[J]. IEEE Transactions on Industrial Electronics,2018,65(11):8788-8796. DOI: 10.1109/TIE.2018.2811365
[12] WANG Yingjie,LIU Feilong,CHEN Shuai,et al. Prediction errors analysis and correction on FCS-MPC for the cascaded H-bridge multilevel inverter[J]. IEEE Transactions on Industrial Electronics,2022,69(8):8264-8273. DOI: 10.1109/TIE.2021.3104594
[13] ZHAO Xiangkun,XU Gaoxiang,WANG Li,et al. A novel clustered voltage balance for cascaded H-bridge STATCOM with CCS-MPC[C]. IEEE 4th International Electrical and Energy Conference,Wuhan,2021:1-6.
[14] YE Manyuan,KANG Lixuan,XIAO Yunhuang,et al. Modified hybrid modulation strategy with power balance control for H-bridge hybrid cascaded seven-level inverter[J]. IET Power Electronics,2018,11(6):1046-1054. DOI: 10.1049/iet-pel.2017.0558
[15] YE Zongbin,WANG Tingting,MAO Shiqi,et al. A PWM strategy based on state transition for cascaded H-bridge inverter under unbalanced DC sources[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2020,8(2):1686-1700. DOI: 10.1109/JESTPE.2019.2893936
[16] YE Zongbin,ZHENG Qisheng,PEI Hanjun,et al. New inter and inner phase power control method for cascaded H-bridge based on simplified PWM strategy[J]. IEEE Transactions on Power Electronics,2020,35(8):8607-8623. DOI: 10.1109/TPEL.2019.2961945
[17] IHOR O,LARYSA A,SERHII B. Research of closed loop control systems of the electric drive of mine electric locomotive with the DC series motor and nonlinear load[C]. IEEE International Conference on Modern Electrical and Energy Systems,Kremenchuk,2021: 1-6.
[18] BAO Jusheng,YANG Shuai,GE Shirong,et al. Design and experiments on a hybrid electric drive system for underground coal mine locomotives[C]. IEEE International Conference on Mechatronics,Robotics and Automation,Hefei,2018:117-121.
[19] GAUTAM A R,FULWANI D M,MAKINENI R R,et al. Control strategies and power decoupling topologies to mitigate 2ω-ripple in single-phase inverters:a review and open challenges[J]. IEEE Access,2020,8:147533-147559. DOI: 10.1109/ACCESS.2020.3015315
[20] 袁义生,毛凯翔. 基于负载电流前馈的级联SCHBR直流电压平衡策略[J]. 电力自动化设备,2019,39(6):33-38,53. YUAN Yisheng,MAO Kaixiang. DC voltage balance strategy for cascaded H-bridge rectifier based on load current feedforward[J]. Electric Power Automation Equipment,2019,39(6):33-38,53.
[21] WATANABE H,SAKURABA T,FURUKAWA K,et al. Development of DC to single-phase AC voltage source inverter with active power decoupling based on flying capacitor DC/DC converter[J]. IEEE Transactions on Power Electronics,2018,33(6):4992-5004. DOI: 10.1109/TPEL.2017.2727063
计量
- 文章访问数: 83
- HTML全文浏览量: 48
- PDF下载量: 14
