Research on the targetless automatic calibration method for mining LiDAR and camera
-
摘要: 矿用车辆实现无人驾驶依赖于准确的环境感知,激光雷达和相机的结合可以提供更丰富和准确的环境感知信息。为确保激光雷达和相机的有效融合,需进行外参标定。目前矿用本安型车载激光雷达多为16线激光雷达,产生的点云较为稀疏。针对该问题,提出一种矿用激光雷达与相机的无目标自动标定方法。利用多帧点云融合的方法获得融合帧点云,以增加点云密度,丰富点云信息;通过全景分割的方法提取场景中的车辆和交通标志物作为有效目标,通过构建2D−3D有效目标质心对应关系,完成粗校准;在精校准过程中,将有效目标点云通过粗校准的外参投影在逆距离变换后的分割掩码上,构建有效目标全景信息匹配度目标函数,通过粒子群算法最大化目标函数得到最优的外参。从定量、定性和消融实验3个方面验证了方法的有效性:① 定量实验中,平移误差为0.055 m,旋转误差为0.394°,与基于语义分割技术的方法相比,平移误差降低了43.88%,旋转误差降低了48.63%。② 定性结果显示,在车库和矿区场景中的投影效果与外参真值高度吻合,证明了该方法的稳定性。③ 消融实验表明,多帧点云融合和目标函数权重系数显著提高了标定精度。与单帧点云相比,使用融合帧点云作为输入时,平移误差降低了50.89%,旋转误差降低了53.76%;考虑权重系数后,平移误差降低了36.05%,旋转误差降低了37.87%。Abstract: The realization of autonomous driving for mining vehicles relies on accurate environmental perception, and the combination of LiDAR and cameras can provide richer and more accurate environmental information. To ensure effective fusion of LiDAR and cameras, external parameter calibration is necessary. Currently, most mining intrinsically safe onboard LiDARs are 16-line LiDARs, which generate relatively sparse point clouds. To address this issue, this paper proposed a targetless automatic calibration method for mining LiDAR and camera. Multi-frame point cloud fusion was utilized to obtain fused frame point clouds, increasing point cloud density and enriching point cloud information. Then, effective targets such as vehicles and traffic signs in the scene were extracted using panoramic segmentation. By establishing a corresponding relationship between the centroids of 2D and 3D effective targets, a coarse calibration was completed. In the fine calibration process, the effective target point clouds were projected onto the segmentation mask after inverse distance transformation using the coarse-calibrated external parameters, constructing an objective function based on the matching degree of effective target panoramic information. The optimal external parameters were obtained by maximizing the objective function using a particle swarm algorithm. The effectiveness of the method was validated from three aspects: quantitative, qualitative, and ablation experiments. ① In the quantitative experiments, the translation error was 0.055 m, and the rotation error was 0.394°. Compared with the method based on semantic segmentation technology, the translation error was reduced by 43.88%, and the rotation error was reduced by 48.63%. ② The qualitative results showed that the projection effects in the garage and mining area scenes were highly consistent with the true values of the external parameters, demonstrating the stability of the method. ③ Ablation experiments indicated that multi-frame point cloud fusion and the weight coefficients of the objective function significantly improved calibration accuracy. When using fused frame point clouds as input compared to single-frame point clouds, the translation error was reduced by 50.89%, and the rotation error was reduced by 53.76%. Considering the weight coefficients, the translation error was reduced by 36.05%, and the rotation error was reduced by 37.87%.
-
0. 引言
近年来,我国煤矿开始加快推进智能化建设,其中矿用无人驾驶辅助运输车辆已成为煤矿智能化建设的重要内容和智能化煤矿验收的重要标准[1-2]。由此可见,矿用车辆向智能化乃至无人化发展是未来发展必然的趋势。然而,矿用车辆要实现无人驾驶,必须要依赖准确的环境感知[3-5],即利用矿用本安型车载传感器进行感知。激光雷达和相机作为最常见的车载传感器,它们具有不同的优劣势。激光雷达可直接获取高精度的距离信息,但无法感知目标表面的纹理和颜色。相机可以提供颜色和纹理信息,易于进行目标的识别与分割,但无法直接提供感知目标的距离信息。将激光雷达和相机相结合可以弥补彼此的不足,从而获得更丰富和准确的环境感知信息,这对于矿用无人驾驶车辆的三维目标检测及同时定位与地图构建(Simultaneous Localization and Mapping,SLAM)建图等至关重要。为了确保激光雷达和相机之间有效融合,需要进行外参(描述传感器之间相对位置和姿态的参数,包括平移向量和旋转矩阵)标定。通过准确估计激光雷达和相机之间的外参,可以将它们的数据对齐,使它们在同一坐标系下具有一致性。一般来说,激光雷达与相机的外参标定方法可以分为基于目标和无目标2类。
文献[6]最早提出了基于目标的标定方法,使用固定的棋盘格作为标定目标。通过优化棋盘格表面的法线来求解校准参数。文献[7]建立了一种新的几何约束来解耦激光雷达和相机之间的旋转和平移,并提出了一个基于平面法线不确定性的权值,以提高外参的准确性。文献[8] 利用激光雷达点云在不同颜色区域的反射率差异,提取棋盘格上的角点信息,从而实现激光雷达与相机标定。文献[9-12]通过建立二维和三维特征空间之间匹配关系来优化外参。上述方法依赖于人工选择特定的目标或使用特殊的标定工具,不仅费时费力,而且难以适应实时标定的需求。
基于无目标的标定方法不需要制作特定的校准目标,直接从环境中获取外观或者运动信息,自动完成外参的估计。文献[13]利用点云反射率与图像灰度值之间的互信息(Mutual Information,MI)最大化来实现外参估计。文献[14]通过给不同场景类别中的3D−2D属性对分配不同的权重,组合出一个可靠的相似度度量。文献[15]利用神经信息估计器(Mutual Information Neural Estimation ,MINE)来估计从点云和图像像素中提取的语义标签的MI。文献[16]通过直线特征提取器提取点云和图像中的直线特征(如车道线、电线杆等),将外参估计看作线特征语义约束下的线匹配问题。文献[17]利用图像语义分割构建二值分割掩码,使点云更多地投影到障碍物的分割区域像素点上。文献[18]基于手眼模型进行2D−3D校准,采用传感器融合里程计优化外参。文献[19]采用运动恢复结构(Structure from Motion,SfM)和最近点迭代(Iterative Closest Point,ICP)算法,对二维图像序列与LiDAR点云进行配准,同时通过结合投影和边缘特征点的组合优化方法,提升了外参精度。然而,由于运动估计误差会影响标定参数的精度,这些方法只能提供粗略的外参标定结果。
近年来,随着深度学习在点云和图像特征提取方面的卓越能力展现,基于深度学习的激光雷达相机标定方法应运而生。文献[20]提出了RegNet,首次使用深度卷积神经网络(Convolutional Neural Networks, CNN)来估计投影深度测量值与图像之间的对应关系,并回归6自由度(Degrees of Freedom,DOF)外部校准参数。文献[21]提出的CalibNet是一个几何监督神经网络,通过最大化输入图像和点云的几何和光度一致性来估计外部校准参数。文献[22]提出了校准流网络(Calibration Flow Network,CFNet),该方法结合几何方法,通过使用双通道图像(校准流)描述初始投影与地面真值之间的偏差,并采用随机样本一致性(Random Sample Consensus,RANSAC)中的EPnP算法,建立校准流构建的2D−3D对应关系来估计外参。上述基于无目标的标定方法虽然能够省去人为干预,但需要提供较为准确的初始标定参数,或者所需激光点云较为稠密,对于点云数据的要求较高。而目前矿用本安型车载激光雷达存在防爆功率要求,常用的多为16线激光雷达,产生的点云较为稀疏。
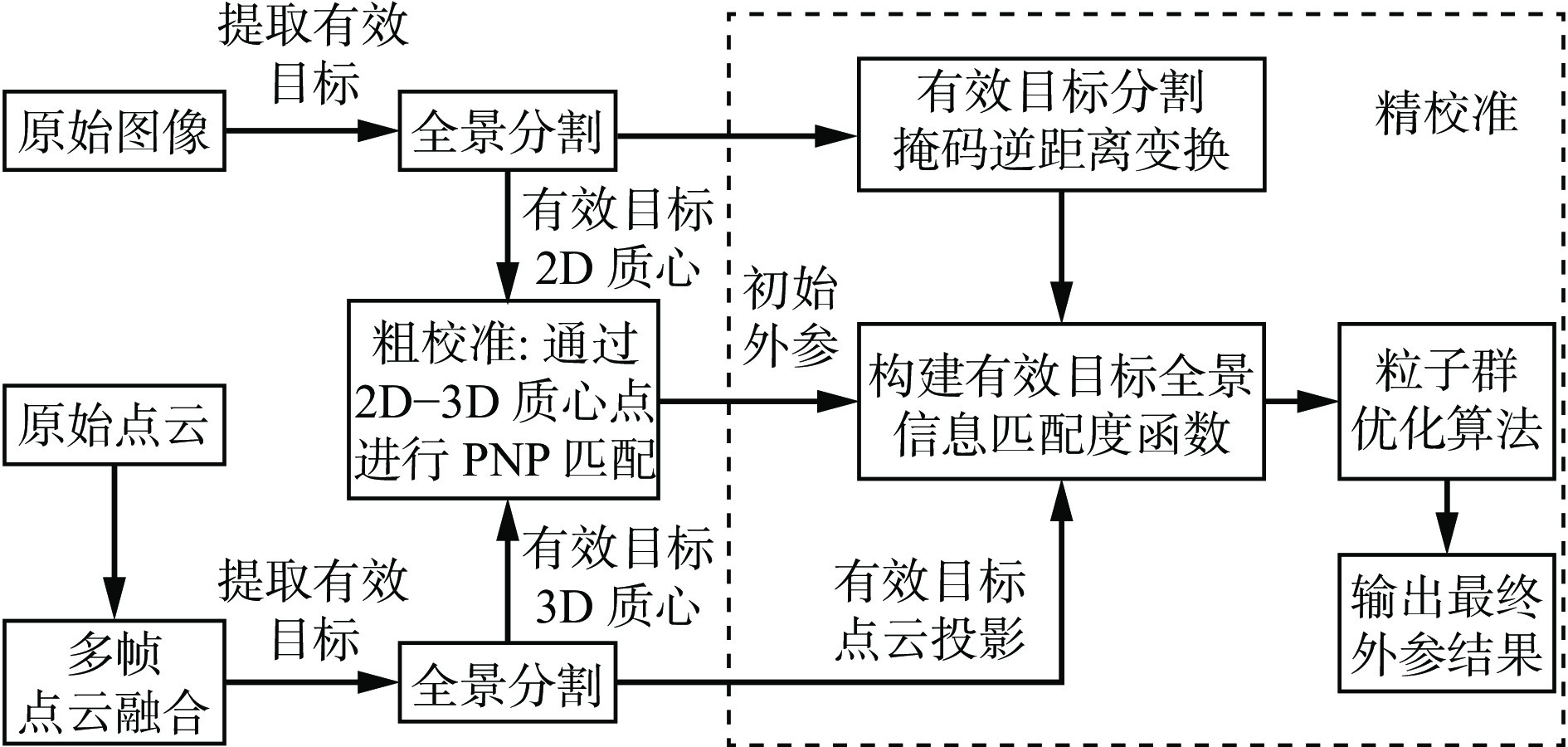
针对矿用本安型车载传感器的特点,本文提出一种矿用激光雷达与相机的无目标自动标定方法。首先利用多帧点云融合的方法获得融合帧点云,以增加点云密度,丰富点云信息;然后通过全景分割的方法提取场景中的车辆和交通标志作为有效目标,通过构建2D−3D有效目标质心对应关系,实现矿用激光雷达与相机外参的粗校准;最后在精校准部分,将有效目标点云通过粗校准的外参投影在逆距离变换后的分割掩码上,构建有效目标全景信息匹配度目标函数,通过粒子群算法最大化目标函数得到最优的外参。
1. 问题分析
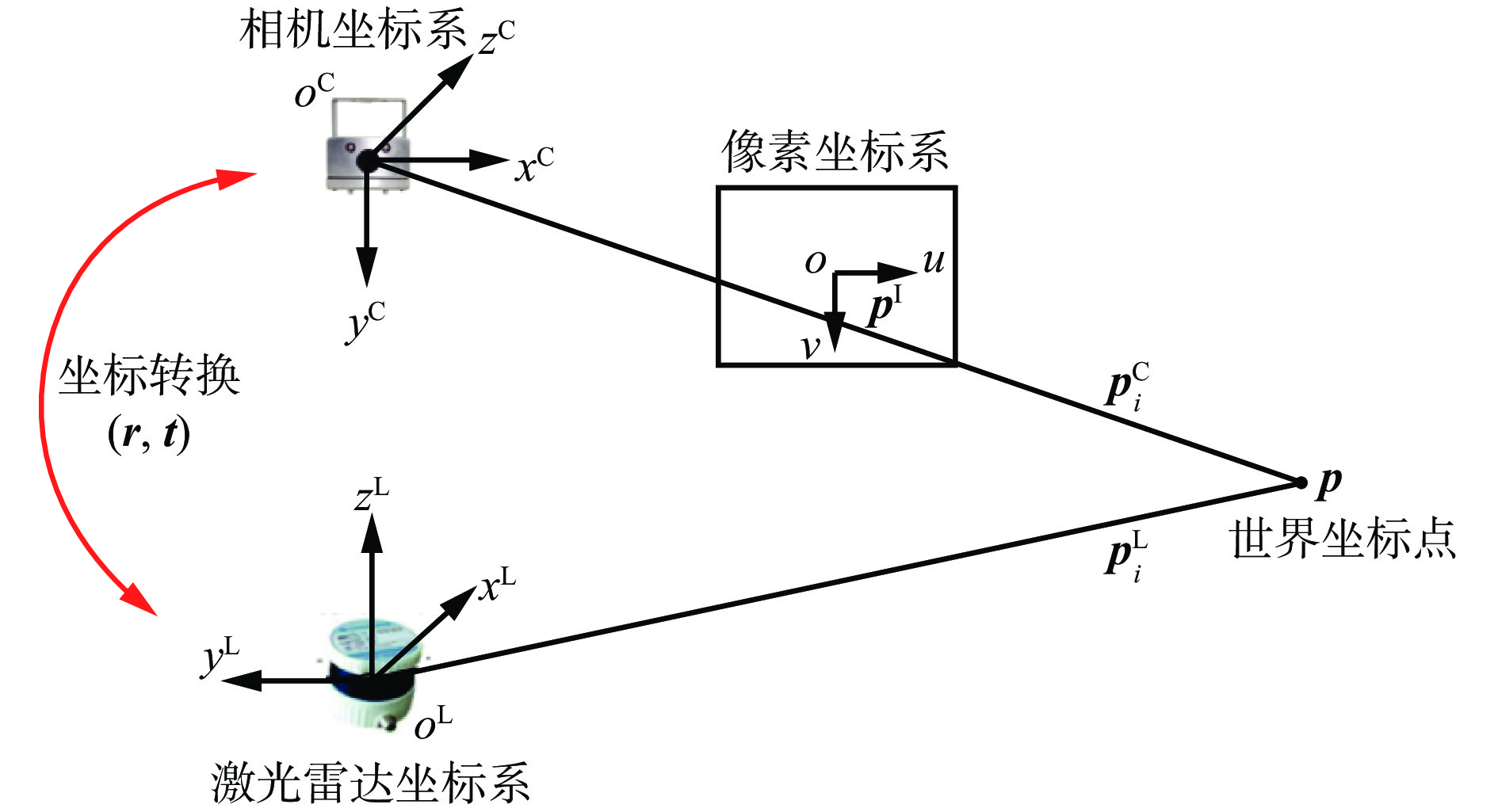
本文目标是对齐点云和场景中的图像,因此需要建立激光雷达与相机之间的映射关系,将激光雷达的点云投影在图像平面上,获得它们之间的几何关系和转换参数,以便将它们投影到同一个坐标系中,其原理如图1所示。激光雷达坐标系坐标点与相机坐标系坐标点的转化参数就是激光雷达和相机的外参。世界坐标系下的点集P在激光雷达坐标系下记为$ {{P}}^{{\mathrm{L}}} $,$ {{P}}^{{\mathrm{L}}}=\left\{{{{\boldsymbol{p}}}}_{1}^{{\mathrm{L}}},{{{\boldsymbol{p}}}}_{2}^{{\mathrm{L}}},\cdots ,{{{\boldsymbol{p}}}}_{n}^{{\mathrm{L}}}\right\} $,$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}}={({x}_{i},{y}_{i},{{\textit{z}}}_{i})}^{\mathrm{T}}\in {\mathbb{R}}^{3} $,n为点云总数,$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}} $为激光雷达坐标系中第i个点,$ ({x}_{i},{y}_{i},{{\textit{z}}}_{i})\mathrm{为}{{p}}_{i}^{{\mathrm{L}}}\mathrm{的}\mathrm{坐}\mathrm{标}{\mathrm{。}\mathrm{将}{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}} $转换为相机坐标系下的点$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{C}}} $:
$$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{C}}}={\boldsymbol{r}} {{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}}+{\boldsymbol{t}} $$ (1) 式中r,t分别为激光雷达到相机的旋转矩阵和平移矩阵。
通过投影函数$ K:{\mathbb{R}}^{3}\to {\mathbb{R}}^{2} $,将相机坐标系中的三维点$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{C}}} $投影到像素坐标系下的像素点$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}}={({u}_{i},{v}_{i})}^{\mathrm{T}}\in {\mathbb{R}}^{2} $,$ ({u}_{i},{v}_{i}) $为$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}} $的坐标,投影函数利用相机的内参(如焦距、畸变等)来计算像素坐标。
$$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}}=K\left({{{\boldsymbol{p}}}}_{i}^{{\mathrm{C}}}\right) $$ (2) 本文中相机的内参是已知数据,重点是探索准确的外参$ \left(\boldsymbol{r},\boldsymbol{t}\right) $。
2. 矿用激光雷达与相机的无目标自动标定方法
矿用激光雷达与相机的无目标自动标定方法由粗校准和精校准组成,如图2所示。
2.1 多帧点云融合
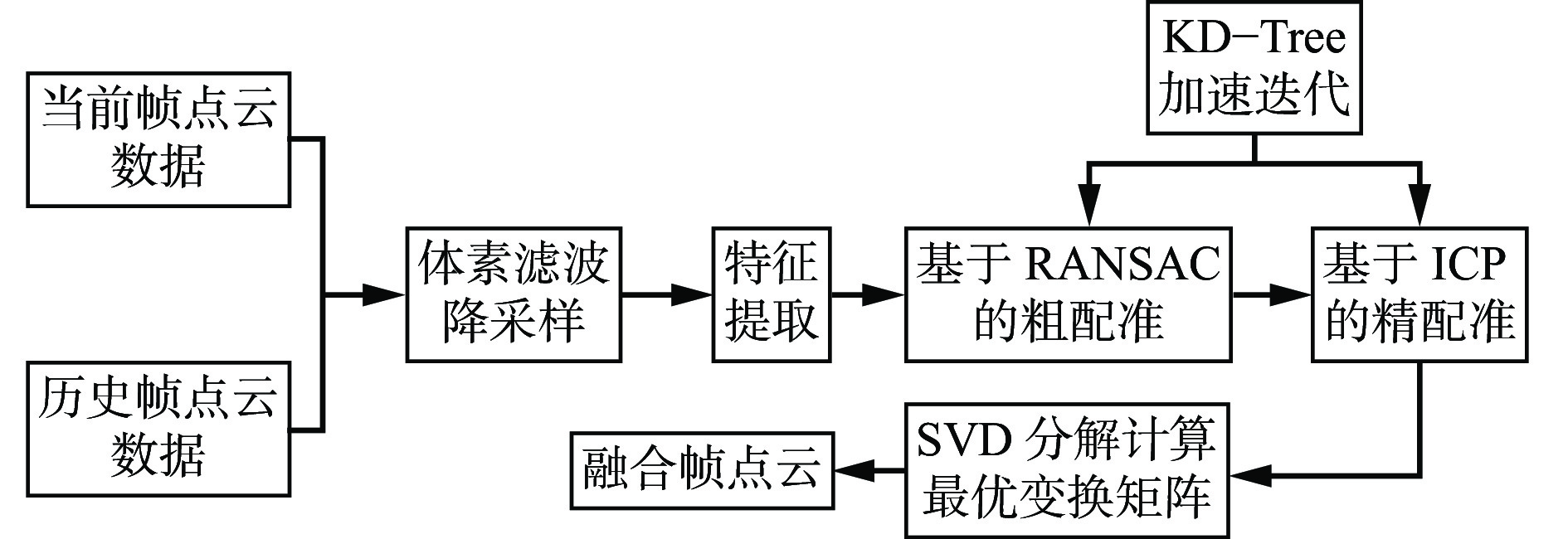
多帧点云融合作为本文方法的重要步骤,影响后续的点云分割任务及外参的标定精度。为了有效平衡计算效率和信息丰富性,避免过高的计算复杂度和信息冗余,选择3帧点云数据,将前2帧作为历史帧点云,然后通过多帧点云融合算法将历史帧点云数据配准到当前帧点云,目的是丰富当前帧点云信息,得到融合帧点云。多帧点云融合算法流程如图3所示。将历史帧点云数据通过基于RANSAC的粗配准方法和当前帧点云数据进行初步对齐,使用基于ICP的精配准方法进一步优化对齐结果,得到更精确的融合帧点云。
1) 基于RANSAC的粗配准。通过RANSAC算法初步对齐历史帧点云和当前帧点云。对当前帧点云数据和历史帧点云数据进行降采样及点云特征描述子 (Fast Persistent Feature Histograms,FPFH)特征的提取。采用KD−Tree方法搜索最近邻点。假设提取到N对特征点,特征点集为$ {\left\{\left({{{\boldsymbol{p}}}}_{{\mathrm{s}}i},{{{\boldsymbol{p}}}}_{{\mathrm{t}}i}\right)\right\}}_{i=1}^{N} $,其中,$ {{{\boldsymbol{p}}}}_{{\mathrm{s}}i} $为历史帧点云中的某一特征点,$ {{\boldsymbol{p}}}_{{\mathrm{t}}i} $为当前帧点云中的某一特征点。
从特征点集中随机选取4个特征点对$ \left\{\left({{{\boldsymbol{p}}}}_{{\mathrm{s}}1},{{{\boldsymbol{p}}}}_{{\mathrm{t}}1}\right),\left({{{\boldsymbol{p}}}}_{{\mathrm{s}}2},{{{\boldsymbol{p}}}}_{{\mathrm{t}}2}\right),\left({{{\boldsymbol{p}}}}_{{\mathrm{s}}3},{{{\boldsymbol{p}}}}_{{\mathrm{t}}3}\right),\left({{{\boldsymbol{p}}}}_{{\mathrm{s}}4},{{{\boldsymbol{p}}}}_{{\mathrm{t}}4}\right)\right\} $,且保证4个点之间非共线。使用选择的特征点对,通过奇异值分解(Singular Value Decomposition,SVD)计算刚体变换矩阵T0,然后使用T0将历史帧点云中所有特征点$ {{{\boldsymbol{p}}}}_{{\mathrm{s}}i} $进行变换,得到变换后的点$ {{{\boldsymbol{p}}}}'_{{\mathrm{s}}i} $:
$$ {{{\boldsymbol{p}}}}'_{{\mathrm{si}}}={\boldsymbol{T}}_{0}{{{\boldsymbol{p}}}}_{{\mathrm{si}}} $$ (3) 计算$ {{{\boldsymbol{p}}}}'_{{\mathrm{si}}} $与当前帧点云中的特征点$ {{{\boldsymbol{p}}}}_{{\mathrm{ti}}} $的距离误差$\xi $,若$\xi $小于设定好的阈值$\varepsilon $,则该点被称为内点。
$$ \mathrm{\xi }=\sum _{i=1}^{N}\delta \left(||{{{\boldsymbol{p}}}}_{{\mathrm{ti}}}-{{{\boldsymbol{p}}}}'_{{\mathrm{si}}}||\right) < \varepsilon $$ (4) 式中$ \delta (\cdot ) $为指示函数,当$ ||{{{\boldsymbol{p}}}}_{{\mathrm{t}}i}-{{{\boldsymbol{p}}}}'_{{\mathrm{s}}i}|| < \varepsilon $时,$ \delta \left(||{{{\boldsymbol{p}}}}_{{\mathrm{t}}i}-{{{\boldsymbol{p}}}}'_{{\mathrm{s}}i}||\right) $=1,否则为0。
重复上述步骤,经过多次迭代,选择内点数量最多的刚体变换矩阵T0作为最终的粗配准结果。
2) 基于ICP的精配准。在RANSAC粗配准后,使用ICP方法进行精配准,以进一步优化变换矩阵。使用RANSAC估计的刚体变换矩阵T0初始化历史帧点云位置,将历史帧点云初步对齐到当前帧点云。使用KD−Tree加速搜索历史帧点云中每个点在当前帧点云中的最近邻点。并建立2帧点云之间的点对关系。然后,定义误差函数以衡量历史帧点云和当前帧点云对应点对之间的距离误差,误差函数为
$$ E\left({\boldsymbol{T}}_{{\mathrm{f}}}\right)=\sum _{i}{||{{{\boldsymbol{p}}}}_{i}'-{\boldsymbol{T}}_{{\mathrm{f}}}{{{\boldsymbol{p}}}}_{i}||}^{2} $$ (5) 式中:$ {{{\boldsymbol{p}}}}_{i} $为历史帧点云中第i个点;$ {{{\boldsymbol{p}}}}_{i}' $为当前帧点云中与$ {{{\boldsymbol{p}}}}_{i} $匹配的最近邻点;$ {\boldsymbol{T}}_{{\mathrm{f}}} $为当前的变换矩阵。
上述误差函数可以通过SVD求解,经过若干次迭代,变换矩阵Tf收敛到一个稳定值,即可得到精确的融合帧点云。
通过以上粗精配准,能够有效地将历史帧点云数据配准到当前帧点云,如图4所示。可看出融合帧点云较当前帧点云密度更大,目标轮廓更清晰完整。
2.2 粗校准
无目标的校准方法对于良好的初始外参要求较高,因为良好的初始化可以加快优化过程的收敛速度,避免发散或陷入局部极小值。目前大多数方法的初始参数都是通过手动方式测量或者手眼校准,但手动测量耗时耗力,手眼校准依赖传感器的运动信息。无目标自动标定方法要实现更准确的外参标定就必须对外参进行初始化校准,参考文献[23],使用语义分割来分别计算图像2D语义质心和激光雷达点云3D语义质心,通过构建2D−3D语义质心对应关系,将激光雷达与相机的粗校准看作一种PnP问题进行解析。常见的PnP算法要求至少有3对点云才能计算,这就要求每对点云和图像必须有3类对象,增加了对于标定场景的限制。本文通过全景分割,为每个像素点和点云分配类别标签和实例ID,并选择容易分割且特征明显的车辆和交通标志分别作为有效目标,进而获取车辆的实例质心及交通标志的语义质心,以此增加2D−3D的对应关系,示例如图5所示。
根据该有效目标m所有有效像素坐标的平均值,得到$ m $的2D质心:
$$ \boldsymbol{B}_m^{\mathrm{I}}=\frac{\displaystyle\sum_{\boldsymbol{q}_i^{\mathrm{I}}\in\boldsymbol{Q}_m^{\mathrm{I}}}^{ }\boldsymbol{q}_i^{\mathrm{I}}}{\left|Q_m^{\mathrm{I}}\right|} $$ (6) 式中:$ {{Q}}_{m}^{{\mathrm{I}}} $为具有有效目标$ m $的像素点集,$ {{Q}}_{m}^{{\mathrm{I}}}= \left\{{{{\boldsymbol{q}}}}_{1}^{{\mathrm{I}}},{{{\boldsymbol{q}}}}_{2}^{{\mathrm{I}}},{\cdots, {{\boldsymbol{q}}}}_{n}^{{\mathrm{I}}}\left|,{{{\boldsymbol{q}}}}_{i}^{{\mathrm{I}}}\right.={({u}_{i},{v}_{i})}^{\mathrm{T}}\in {\mathbb{R}}^{2}\right\} $;$ \left|{{Q}}_{m}^{{\mathrm{I}}}\right| $为有效目标 $ m $的像素点个数。
根据所有有效点云坐标的平均值,得到有效目标$ m $在激光雷达坐标系下的3D质心:
$$ \boldsymbol{B}_m^{\rm{L}}=\frac{\displaystyle\sum_{\boldsymbol{p}_i^{\rm{L}}\in\boldsymbol{P}_m^{\rm{L}}}^{ }\boldsymbol{p}_i^{\rm{L}}}{\left|P_m^{\rm{L}}\right|} $$ (7) 式中:$ {{P}}_{m}^{{\mathrm{L}}} $为具有有效目标$ m $的点云集,$ {P}_{m}^{{\mathrm{L}}}= \left\{{{{\boldsymbol{p}}}}_{1}^{{\mathrm{L}}},{{{\boldsymbol{p}}}}_{2}^{{\mathrm{L}}},{\cdots ,{{\boldsymbol{p}}}}_{n}^{{\mathrm{L}}}\left|,{{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}}\right.={({x}_{i},{y}_{i},{{\textit{z}}}_{i})}^{\mathrm{T}}\in {\mathbb{R}}^{3}\right\} $;$ \left|{P}_{m}^{{\mathrm{I}}}\right| $为有效目标$ m $的点云个数。
通过以上定义,可以得到有效目标的2D−3D质心对。由于一些PnP线性方法(如P3P)难以利用更多的点对匹配信息,本文选择EPnP方法对激光雷达与相机的初始外参进行估计,得到一组良好的初始标定参数($ {\boldsymbol{r}}_{0},{\boldsymbol{t}}_{0} $),供精校准使用。
EPnP方法是通过PCA构建4个控制点,将这4个控制点线性组合表示有效目标的3D质心坐标,假设有D个有效目标,第i个有效目标3D质心为$ {{{\boldsymbol{B}}}}_{i}^{{\mathrm{L}}}=\left({x}_{i}^{{\mathrm{L}}},{y}_{i}^{{\mathrm{L}}},{{\textit{z}}}_{i}^{{\mathrm{L}}}\right) $。使用控制点来表示每个3D质心点:
$${{{\boldsymbol{B}}}}_{i}^{\rm{L}}=\sum _{j=1}^{4}{\gamma }_{ij}{{{\boldsymbol{c}}}}_{j}^{\rm{L}} $$ (8) 式中:$ {\gamma }_{ij} $为权重,满足$ \displaystyle \sum_{j=1}^{4}{\gamma }_{ij}=1 $;$ {\boldsymbol{c}}_j^{\mathrm{L}} $为3D目标质心对应的控制点坐标,$ {{{\boldsymbol{c}}}}_{j}^{{\mathrm{L}}}=({x}_{j}^{{\mathrm{L}}},{y}_{j}^{{\mathrm{L}}},{{\textit{z}}}_{j}^{{\mathrm{L}}}) $。
同理,相机坐标系下$ {{{\boldsymbol{c}}}}_{i}^{{\mathrm{C}}} $用控制点线性组合表示:
$$ \boldsymbol{B}_i^{\mathrm{C}}=\sum_{j=1}^4\gamma_{ij}\left(\boldsymbol{r}_0\boldsymbol{c}_j^{\mathrm{L}}+\boldsymbol{t}_0\right)=\sum_{j=1}^4\gamma_{ij}\boldsymbol{c}_j^{\mathrm{C}} $$ (9) 式中$ {{{\boldsymbol{c}}}}_{j}^{{\mathrm{C}}} $为相机坐标系下对应的控制点坐标,$ {{{\boldsymbol{c}}}}_{j}^{{\mathrm{C}}}=({x}_{j}^{{\mathrm{C}}},{y}_{j}^{{\mathrm{C}}},{{\textit{z}}}_{j}^{{\mathrm{C}}}) $。
利用相机的投影关系将相机坐标系下的点$ {{\boldsymbol{c}}}_{i}^{{\mathrm{C}}} $投影到像素坐标系下的点$ {{{\boldsymbol{c}}}}_{i}^{{\mathrm{I}}}={({u}_{i},{v}_{i})}^{{\mathrm{T}}} $上。
$$ {Z}_{i}^{{\mathrm{C}}}\left[\begin{array}{c}{u}_{i}\\ {v}_{i}\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_{u}& 0& {u}_{c}\\ 0& {f}_{v}& {v}_{c}\\ 0& 0& 1\end{array}\right]\sum _{j=1}^{4}{\gamma }_{ij}\left[\begin{array}{c}{x}_{j}^{{\mathrm{C}}}\\ {y}_{j}^{{\mathrm{C}}}\\ {{\textit{z}}}_{j}^{{\mathrm{C}}}\end{array}\right] $$ (10) 式中:$ {Z}_{i}^{{\mathrm{C}}} $为坐标点的投影深度;$ {f}_{{\mathrm{u}}} $,$ {f}_{{\mathrm{v}}} $,$ {u}_{{\mathrm{c}}} $,$ {v}_{{\mathrm{c}}} $为相机内部参数,此数据都为已知数据。
将式(10)展开可得:
$$ \left\{\begin{array}{c}\displaystyle \sum _{j=1}^{4}{\gamma }_{ij}{f}_{{\mathrm{u}}}{x}_{j}^{{\mathrm{C}}}+{\gamma }_{ij}\left({u}_{{\mathrm{c}}}-{u}_{i}\right){{\textit{z}}}_{j}^{{\mathrm{C}}}=0\\ \displaystyle \sum _{j=1}^{4}{\gamma }_{ij}{f}_{{\mathrm{v}}}{y}_{j}^{{\mathrm{C}}}+{\gamma }_{ij}\left({v}_{{\mathrm{c}}}-{v}_{i}\right){{\textit{z}}}_{j}^{{\mathrm{C}}}=0\end{array}\right. $$ (11) 式(11)中仅有相机坐标系下4个控制点坐标未知,$ ({x}_{j}^{{\mathrm{C}}},{y}_{j}^{{\mathrm{C}}},{{\boldsymbol{z}}}_{j}^{{\mathrm{C}}}) $共计12个未知数,当粗校准有D个匹配对时,可将式(11)变成一个线性方程组:
$${\boldsymbol{M}}{{G}}=0$$ (12) 式中:$ {\boldsymbol{M}} $为线性方程的系数矩阵,大小为2D×12;$ {G} $为待求解的相机坐标系下4个控制点坐标。
根据欧氏变换的保距性,可求出相机坐标系下4个控制点的坐标,从而将3D到2D的PNP问题转换为3D到2D的刚体变换问题,最后利用ICP迭代求解激光雷达与相机之间的初始标定参数($ {\boldsymbol{r}}_{0},{\boldsymbol{t}}_{0} $)。
2.3 精校准
2.3.1 构建目标匹配度函数
在精校准过程中,通过图像的全景分割生成逐像素有效目标/背景分割,构建目标匹配图${\mathcal{L}} $:$ {\mathbb{R}}^{2}\to \mathbb{R} $:
$$ {h}_{i}={\mathcal{L}}\left({{{\boldsymbol{q}}}}_{i}^{{\mathrm{I}}}\right)$$ (13) 式中$ {h}_{i} $为像素点$ {\boldsymbol{q}}_{i}^{{\mathrm{I}}} $的匹配值。
对于激光雷达数据,将有效目标的点云$ {{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}}\in {\mathbb{R}}^{3} $经过投影转换为像素坐标系中的像素点$ {{{\boldsymbol{p}}}}_{i}^{I}\in {\mathbb{R}}^{2} $,其匹配值为
$$ {h}_{i}={\mathcal{L}}\left({{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}}\right)={\mathcal{L}}\left[K\left(\boldsymbol{r} {{{\boldsymbol{p}}}}_{i}^{{\mathrm{L}}}+\boldsymbol{t}\right)\right] $$ (14) 最简单的匹配图可以表示为二进制掩码${\mathcal{L}}_{{\mathrm{S}}} $,将有效目标的像素$ \mathbb{V}\subset{{{\mathbb{R}}}}^2 $和其他像素$ \mathbb{O}\subset{{\mathbb{R}}}^2 $分别设置为1和0,则
$$ {\mathcal{L}}_{{\mathrm{S}}}\left({{{\boldsymbol{q}}}}_{i}^{{\boldsymbol{I}}}\right)=\left\{\begin{array}{*{20}{c}}0& {{{\boldsymbol{q}}}}_{i}^{{\mathrm{I}}}\in \mathbb{O}\\ 1&{{{\boldsymbol{q}}}}_{\boldsymbol{i}}^{\rm{I}}\in \mathbb{V}\end{array}\right. $$ (15) 首先,对掩码$ {\mathcal{L}}_{{\mathrm{S}}} $进行逆距离变换(Inverse Distance Transformation,IDT),以防止二值图在相机的观测轴方向上存在零空间问题[18],避免在后续优化过程中出现局部最大值,通过实现距离变换来奖励投影在掩码边缘附近的有效目标点云,匹配值可以从掩码的边界到其内部逐渐衰减,进而平滑目标函数。
$$ \begin{split} & \mathcal{L}_{\mathrm{DT}}\left(m_i^{\mathrm{I}}\right)=\alpha\mathcal{L}_{\mathrm{S}}\left(m_i^{\mathrm{I}}\right)+ \\ & \left(1-\alpha\right)\mathrm{max}_{\boldsymbol{q}_i^I\in\boldsymbol{O}}\mathcal{L}_{\mathrm{S}}\left(m_i^{\mathrm{I}}\right)\beta^{||\boldsymbol{m}_i^{\mathrm{I}}-\boldsymbol{q}_i^{\mathrm{I}}||_1}\quad m_i^{\mathrm{I}}\in\boldsymbol{V}\end{split} $$ (16) 式中$ \alpha $,$ \beta $为平衡系数,用于控制不同项对距离的影响,这里取$ \alpha $=0.8,$ \beta $=0.6。
将式(15)中的匹配图重新定义为
$$ {\mathcal{L}}_{{\mathrm{F}}}\left({{q}}_{i}^{{\mathrm{I}}}\right)=\left\{\begin{array}{*{20}{l}}0,&{{{\boldsymbol{q}}}}_{i}^{{\mathrm{I}}}\in \mathbb{O}\\ {\mathcal{L}}_{{\mathrm{DT}}}\left({{{\boldsymbol{q}}}}_{i}^{I}\right),&{{{\boldsymbol{q}}}}_{i}^{{\mathrm{I}}}\in \mathbb{V}\end{array}\right.$$ (17) 然后,为表示有效目标点云的投影像素与其对应掩码在图像中的一致性,将有效目标$ m $的匹配度定义为
$${S} _{m}=\frac{\displaystyle \sum _{{{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}}\in {{\boldsymbol{P}}}_{m}^{{\mathrm{I}}}}{\mathcal{L}}_{{\mathrm{F}}}\left({{{\boldsymbol{p}}}}_{i}^{{\mathrm{I}}}\right)}{\left|{P}_{m}^{{\mathrm{I}}}\right|} $$ (18) 匹配度越大,则外参越准确。不同的有效目标点云个数不同,在最终的目标函数中每个有效目标占有的重要性也不同。根据投影在匹配图上有效目标的点数分配不同的权重参数,将最终的目标函数定义为
$$ \left\{ \begin{array}{l}U=\displaystyle \sum _{m=1}^{D}{w}_{m}{S} _{m}\\ {w}_{m}=\frac{\left|{P}_{m}^{{\mathrm{I}}}\right|}{\displaystyle \sum _{m=1}^{D}\left|{P}_{m}^{{\mathrm{I}}}\right|}\end{array}\right. $$ (19) 式中wm为有效目标m的加权系数。
最后,通过直接优化目标函数$ U $进一步细化粗校准外参,目标函数值越大,外参越准确,因此,通过最大化目标函数得到最优外部参数 $ (\hat{\boldsymbol{r}},\hat{\boldsymbol{t}}) $:
$$ \left(\hat{\boldsymbol{r}},\hat{\boldsymbol{t}}\right)={\mathrm{arg}}\underset{\left(\boldsymbol{r},\boldsymbol{t}\right)}{\mathrm{max}}U\left(\boldsymbol{r},\boldsymbol{t}\right) $$ (20) 2.3.2 优化目标函数
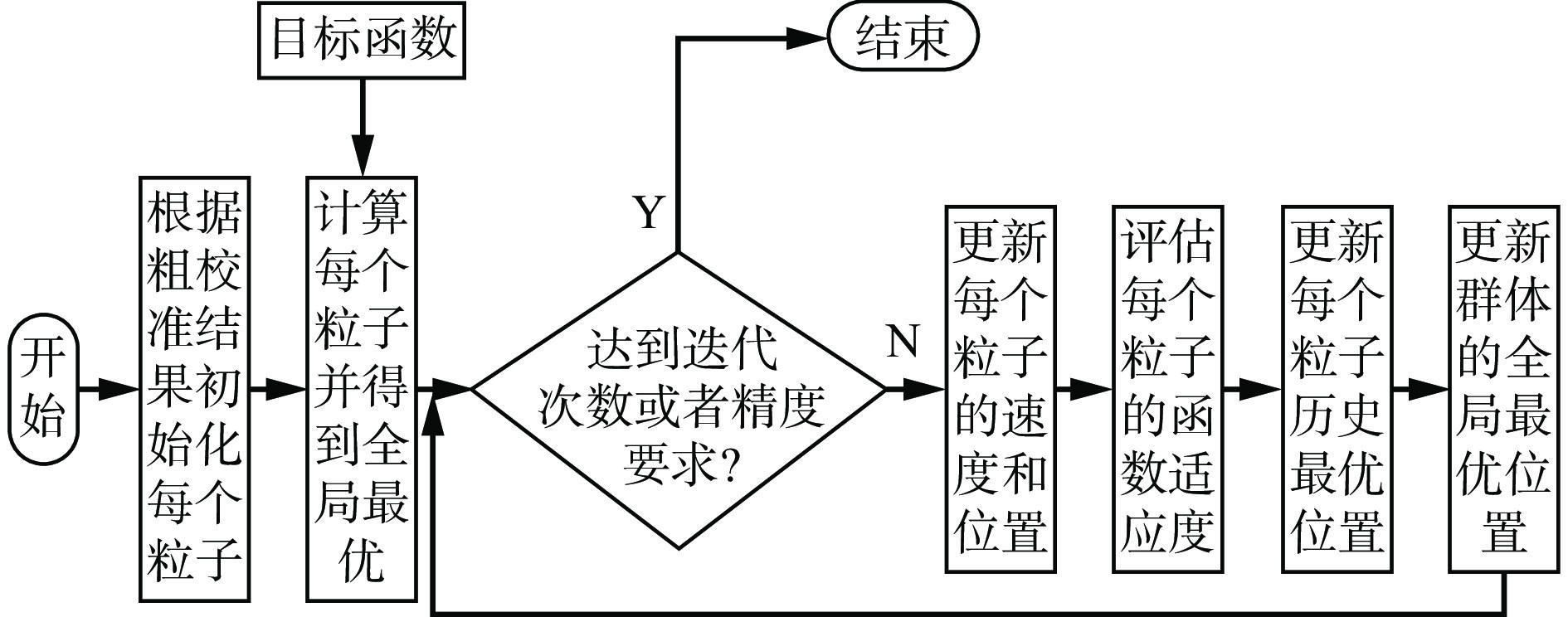
由于本文的目标函数是一个非凸函数,一些经典的优化方法(如梯度下降法和牛顿法)不适用,所以采用粒子群优化方法对目标函数进行优化。粒子群优化算法模拟了鸟群或鱼群的移动行为,通过个体间的信息共享来寻找最优解。每个粒子代表1个候选解,并通过更新其速度和位置进行搜索。流程如图6所示。
1) 初始化粒子群。设定粒子群的数量为F,F=50,每个粒子的维度 d=6,对应$ \boldsymbol{r}={({r}_{x},{r}_{y}{,r}_{{\textit{z}}})}^{{\mathrm{T}}} $和$ \boldsymbol{t}={({t}_{x},{t}_{y}{,t}_{{\textit{z}}})}^{{\mathrm{T}}} $。其中第i个粒子位置位于$ {{{\boldsymbol{Y}}}}_{i}= ({r}_{xi},{r}_{yi}, {r}_{{\textit{z}}i},{t}_{xi},{t}_{yi},{t}_{{\textit{z}}i}) $,速度为$ {{{\boldsymbol{V}}}}_{i}=({v}_{xi},{v}_{yi},{v}_{{\textit{z}}i},{u}_{xi},{u}_{yi},{u}_{{\textit{z}}i}) $,且i=0,1$,\cdots , $F−1。
将粗校准的参数($ {\boldsymbol{r}}_{0},{\boldsymbol{t}}_{0} $)作为第1个粒子的初始位置:
$$ {{{\boldsymbol{Y}}}}_{0}=\left({\boldsymbol{r}}_{0},{\boldsymbol{t}}_{0}\right) $$ (21) 通过在初始解的基础上添加随机小扰动$ {e } $来初始化其他粒子的位置:
$${{{\boldsymbol{Y}}}}_{\boldsymbol{i}}=\left({\boldsymbol{r}}_{0},{\boldsymbol{t}}_{0}\right)+{\boldsymbol{e}} $$ (22) 2) 计算各粒子的适应值。第k次迭代时,将第i个粒子的当前位置代入目标函数计算其适应度,以目标函数最大值为目标。在每次迭代时,每个粒子都会更新其个体最优位置 $ {\boldsymbol{\tau }}_{{\mathrm{best}},i}^{k} $,并在所有粒子中选出全局最优位置 $ {\boldsymbol{g}}_{{\mathrm{best}}}^{k} $。
3) 更新速度和位置。粒子根据个体和全局最优位置调整速度和位置,逐步逼近最优解。
速度更新公式为
$$ {{{\boldsymbol{V}}}}_{i}^{k+1}=\mu {{{\boldsymbol{V}}}}_{i}^{k+1}+{\rho }_{1}{\varphi }_{1}\left({{{\boldsymbol{\tau}} }}_{{\mathrm{best}},i}^{k}-{{{\boldsymbol{Y}}}}_{i}^{k}\right)+{\rho }_{2} {\varphi }_{2} \left({{{\boldsymbol{g}}}}_{{\mathrm{best}}}^{k}-{{{\boldsymbol{Y}}}}_{i}^{k}\right)\;\;\; $$ (23) 式中:$ \mu $为惯性权重;$ {\rho }_{1} $,$ {\rho }_{2} $为学习因子;$ {\varphi }_{1} $,$ {\varphi }_{2} $为[0,1]区间的随机数。
惯性权重表示粒子保留目前速度的程度,较大的惯性权重可以提高算法的全局收敛能力,较小的惯性权重可以提高算法的局部收敛能力。在计算开始时选取$ \mu $的最大值,随着不断迭代,线性递减$ \mu $值,以此来动态调整粒子的搜索能力。
$$ \mu ={\mu }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\frac{k}{{k}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\mu }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mu }_{\mathrm{m}\mathrm{i}\mathrm{n}}\right) $$ (24) 式中:$ {\mu }_{\mathrm{m}\mathrm{a}\mathrm{x}} $,$ {\mu }_{\mathrm{m}\mathrm{i}\mathrm{n}} $分别为权重的最大值和最小值;k为迭代次数;$ {k}_{\mathrm{m}\mathrm{a}\mathrm{x}} $为最大迭代次数。
根据速度对粒子位置进行更新:
$$ {{{\boldsymbol{Y}}}}_{i}^{k+1}={{{\boldsymbol{Y}}}}_{i}^{k}+{{{\boldsymbol{V}}}}_{i}^{k+1}$$ (25) 4) 检查终止条件。如果达到最大迭代次数或精度条件,则输出最优解,否则返回步骤2)。
3. 实验分析
3.1 实验设置
为了验证本文方法的准确性及鲁棒性,在自制数据集上进行了大量实验,将实验采集仪器(图7)安装在无轨胶轮车上进行数据采集。图像来自KBA12(B)矿用本安型摄像仪,分辨率为1 920×1 080,原始点云数据来自16线GUJ50矿用本安型激光雷达。采集场景包括室内车库及矿区室外环境,该数据集以10 Hz的速率同步并校正,其包含了1 120帧RGB图像及时间戳对应的融合帧点云数据,并通过手动测量获得传感器之间的外参作为实验真实值。
本文采用目前分割性能较好的OneFormer模型[24]和P3Former[25]模型分别对当前帧图像和融合帧点云进行全景分割。首先,将自制数据集中的原始图像和融合帧点云制作为Cityscape和Semantic−KITTI格式,训练集与验证集的比例为9∶1。为了加快2个全景分割模型在自制数据集上的收敛速度,本文使用了2个全景分割模型分别在Cityscape数据集和Semantic−KITTI数据集上的预训练权重文件,然后再对2个分割模型进行训练,最终将训练好的模型用于分割预测。
为了评估本文方法相对于参考校准的性能,根据预测的外部参数的平移和旋转误差对标定结果进行分析。通过欧氏距离计算平移误差$\Delta {{t}} $和旋转误差$\Delta {{\theta}} $。
$$ \Delta {{t}}={||{\hat{{\boldsymbol{t}}}}-{\boldsymbol{t}}_{{\mathrm{f}}}||}_{2}$$ (26) $$ \Delta {{\theta}} ={||\hat{\boldsymbol{r}}-{\boldsymbol{r}}_{{\mathrm{f}}}||}_{2}$$ (27) 式中$ {\boldsymbol{t}}_{{\mathrm{f}}} $和$ {\boldsymbol{r}}_{{\mathrm{f}}} $分别为平移向量和旋转向量的真实值。
计算平移的3个分量($ X,Y,Z $)的平均绝对误差(Mean Absolute Error,MAE)$\Delta X ,\Delta Y, \Delta Z$及3个欧拉角(横滚角$ R、\mathrm{俯}\mathrm{仰}\mathrm{角}H、\mathrm{航}\mathrm{向}\mathrm{角}A $)的MAE $\Delta R, \Delta H, \Delta A $。MAE 可衡量平移和旋转预测值与真实值的平均偏差程度。
3.2 定量结果
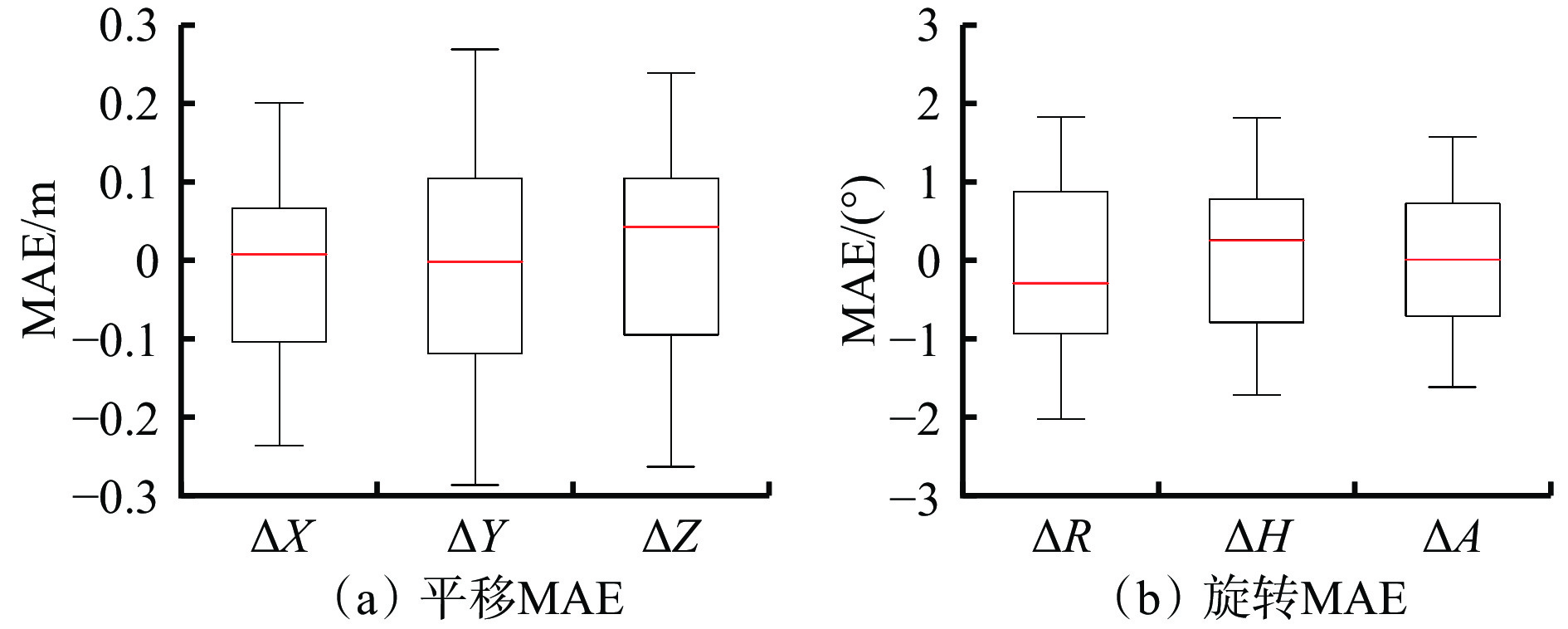
首先,在自制数据集中进行粗校准,整个过程是自动的,本文使用50帧图像和融合点云进行基于有效目标质心的初始化实验,之后不再进行粗校准。粗校准中6个参数的误差分布如图8所示。 X,Y,Z的MAE大多小于0.3 m,R,H,A的MAE大多小于2 °,说明粗校准能给出较合理的初始值。
进行粗校准后,从数据集中2个场景选择100帧图像和融合点云进行精校准实验。所有精校准实验均使用粗校准得到的相同初始外参。2种校准结果见表1,可看出精校准在精度方面较粗校准有了极大的提升。
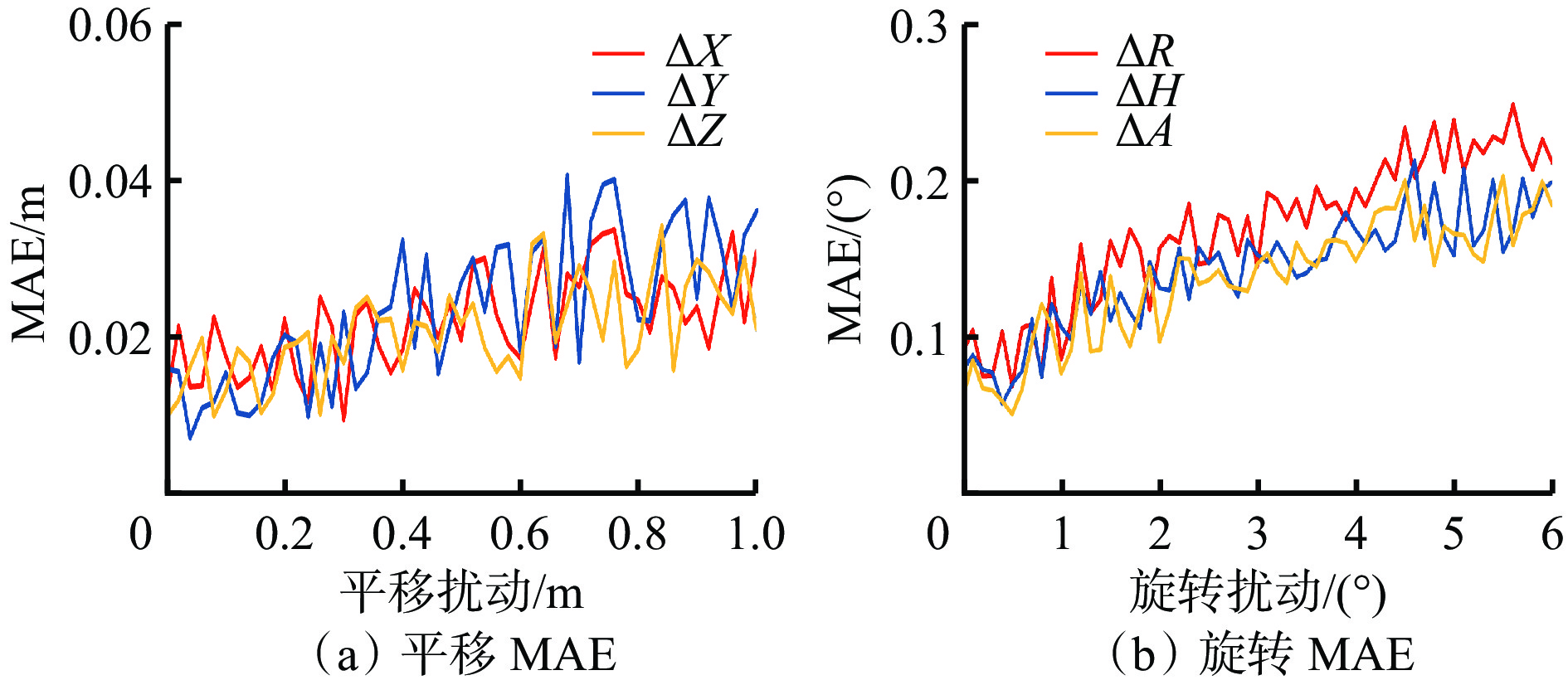
表 1 粗校准和精校准的结果对比Table 1. Comparison of coarse and fine calibration results方法 $ \mathrm{\Delta }t $/m $ \mathrm{\Delta }X $/m $ \mathrm{\Delta }Y $/m $ \mathrm{\Delta }Z $/m $ \mathrm{\Delta }\theta $/(°) $ \mathrm{\Delta }R $/(°) $ \mathrm{\Delta }H $/(°) $ \mathrm{\Delta }A $/(°) 粗校准 0.195 0.096 0.124 0.114 0.991 0.929 0.778 0.991 精校准 0.055 0.031 0.028 0.036 0.394 0.257 0.212 0.205 为了验证精校准的鲁棒性,本文对每个标定参数进行了不同程度的扰动。其中,当1个参数发生改变时,其他5个参数保持其真实值。旋转的扰动范围设置为 [0, 6°],共计60组;平移的扰动范围设置为[0, 1 m],共计50组。每组实验的扰动程度逐步增加,旋转扰动每次增加0.1°,平移扰动每次增加0.02 m。单次扰动在100帧图像和融合点云上进行实验,并将100帧精校准的结果取平均值作为最终结果。
增加扰动后,精校准的MAE如图9所示。可看出尽管初始扰动增大了精校准的难度,但平移和旋转的MAE仅略有增加。这表明扰动的程度对精校准的影响并不显著,说明本文的精校准方法具有鲁棒性和稳定性。
标定参数扰动实验整体结果见表2,可看出平移参数和旋转参数的扰动对精校准影响较小,扰动后的标定参数经过精校准后均能够将误差控制在小于粗校准误差的范围内。
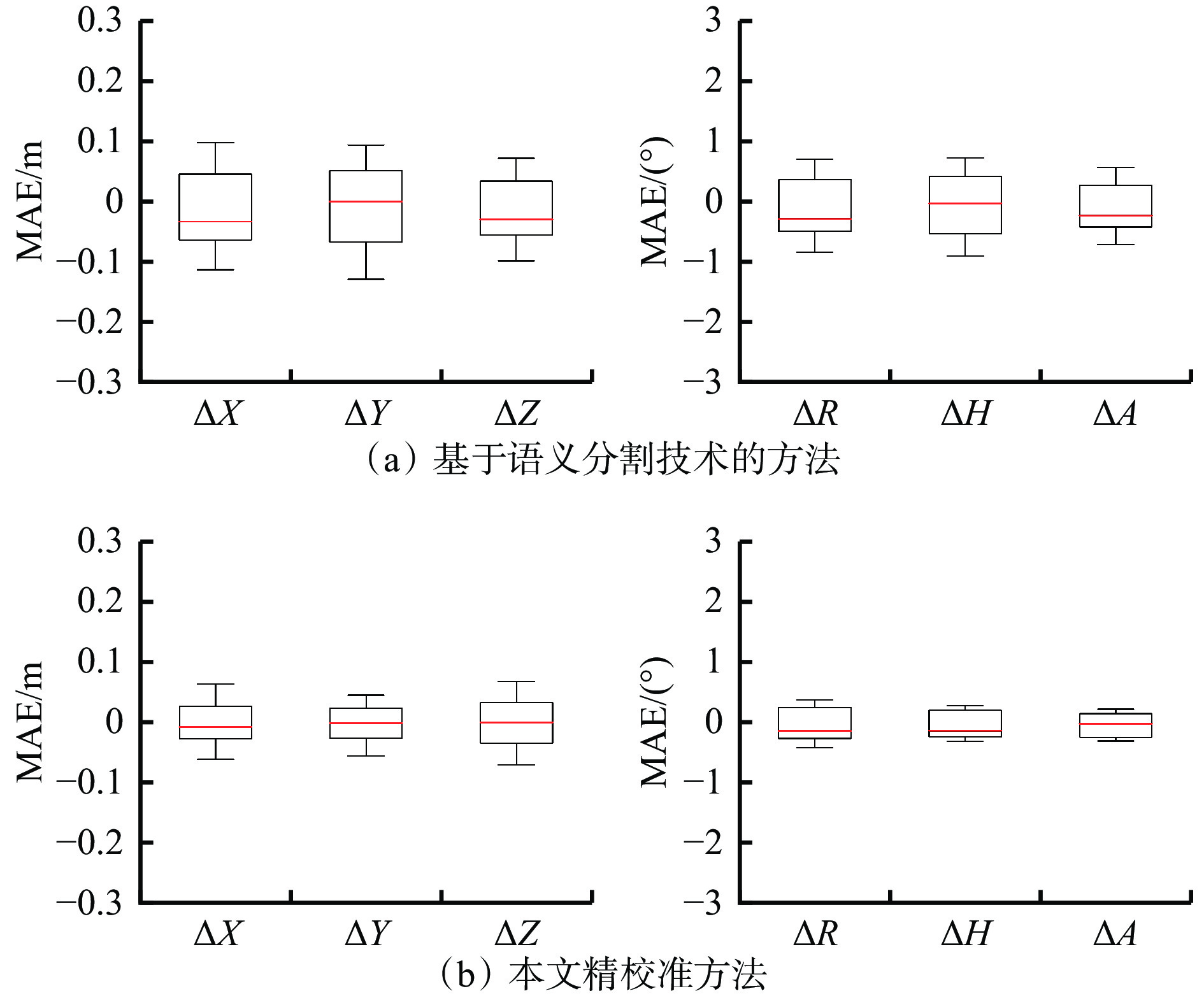
表 2 标定参数扰动实验整体结果Table 2. Overall results of the perturbation experiments on calibration parameters参数 平均值 标准差 最大值 最小值 $ \Delta X $ 0.0223 m0.0062 0.0339 m0.0097 m$ \Delta $Y 0.0238 m0.0094 0.0409 m0.0073 m$ \Delta Z $ 0.0210 m0.0062 0.0326 m0.0099 m$ \Delta $R 0.1689 °0.0477 0.2490 °0.0691 °$ \Delta $H 0.1434 °0.0372 0.2132 °0.0578 °$ \Delta $A 0.1371 °0.0389 0.2035 °0.0512 °为了验证本文方法的先进性,将其与文献 [17] 中基于语义分割技术的方法进行对比。在自制数据集上采用相同的初始外参,使用融合帧点云与图像作为输入开展实验,实验共使用100帧数据,标定结果的MAE见表3。不同方法的校准误差分布如图10所示。由表3和图10可看出,本文方法的平移误差为0.055 m,旋转误差为0.394°,平移误差较基于语义分割技术的方法降低了43.88%,旋转误差降低了48.63%。这是由于本文利用的全景信息能够提供更准确的目标位置和边界信息,有助于降低目标间的相互干扰。本文通过历史帧点云与当前帧点云融合的方法,增加了当前帧中有效目标点云的密度。这种方法不仅丰富了点云数据,还提高了点云的匹配信息,从而降低了校准误差。
表 3 不同方法的校正结果对比Table 3. Comparison of correction results across different methods方法 平移误差/m 旋转误差/(°) $ \mathrm{\Delta }t $ $ \mathrm{\Delta }X $ $ \mathrm{\Delta }Y $ $ \mathrm{\Delta }Z $ $ \mathrm{\Delta }\theta $ $ \mathrm{\Delta }R $ $ \mathrm{\Delta }H $ $ \mathrm{\Delta }A $ 文献[17] 0.098 0.059 0.064 0.047 0.767 0.445 0.497 0.374 精校准 0.055 0.031 0.028 0.036 0.394 0.257 0.212 0.205 3.3 定性结果
为了更直观地显示校准结果,利用表3中精校准的外参将有效目标点云投影到图像平面上。在自制数据集上的2个场景分别进行测试,本文方法的投影结果与外参真值的投影结果如图11所示。从图11(a)和图11(c)可看出,所有车辆和交通标志的图像与点云都能很好对齐,且与图11(b)和图11(d)中外参真值的投影结果非常接近。这表明本文方法在外参标定中具有良好的准确性和稳定性。
3.4 消融研究
比较融合帧点云作为输入和目标函数中的权重系数对整体方法的影响。
1) 融合帧点云作为输入的影响。多帧点云融合可以提高点云的密度和全景分割的质量,为了评估融合帧点云对校准结果的影响,设置2种点云数据输入,一种为融合帧点云,一种为单帧点云,结果见表4。可看出使用融合帧点云相较单帧点云作为输入时平移误差降低了50.89%,旋转误差降低了53.76%,表明多帧点云融合能够有效提高校准精度。
表 4 不同点云输入的消融研究Table 4. Ablation study on different point cloud inputs实验设置 $ \mathrm{平}\mathrm{移}\mathrm{误}\mathrm{差}/\mathrm{m} $ $ \mathrm{旋}\mathrm{转}\mathrm{误}\mathrm{差} $/(°) 单帧点云 0.112 0.852 融合帧点云 0.055 0.394 2) 权重系数的影响。为了评估目标函数中权重系数对校准结果的影响,对权重系数进行了消融实验,结果见表5。不同的有效目标点云个数不同,根据投影在匹配图上有效目标的点数分配不同的权重参数,在相同的测试条件和数据集下运行,一个考虑权重系数,一个不考虑权重系数。可看出考虑权重系数后平移误差降低了36.05%,旋转误差降低了37.87%,表明考虑权重系数可以有效提高校准性能。
表 5 权重系数的消融研究Table 5. Ablation study of weight coefficients实验设置 $ \mathrm{平}\mathrm{移}\mathrm{误}\mathrm{差}/\mathrm{m} $ $ \mathrm{旋}\mathrm{转}\mathrm{误}\mathrm{差} / $(°) 不考虑权重 0.086 0.634 考虑权重 0.055 0.394 4. 结论
1) 提出了一种矿用激光雷达与相机的无目标自动标定方法。针对矿用激光雷达低线束的特点,采用多帧点云融合技术来增加点云密度,以丰富点云信息。通过全景分割技术提取场景中的车辆和交通标志等有效目标,构建2D−3D目标质心对应关系进行粗校准,获得初始外参。随后,将提取的有效目标点云通过初始外参投影到分割掩码上,构建全景信息的匹配度函数,使用粒子群算法对外参进行优化,以提升标定精度。
2) 在定量分析中,矿用激光雷达与相机的无目标自动标定方法的平移误差为0.055 m,旋转误差为0.394°,与基于语义分割技术的方法相比,平移误差降低了43.88%,旋转误差降低了48.63%。
3) 定性结果显示,车库和矿区场景中的投影结果与外参真值高度吻合,点云与图像对齐良好,证明了该方法在实际应用中的稳定性和准确性。
4) 消融实验结果表明,多帧点云融合和目标函数权重系数对标定精度提升有显著作用。使用融合多帧点云相比单帧点云,平移误差降低了50.89%,旋转误差降低了53.76%;而在考虑权重系数后,平移误差降低了36.05%,旋转误差降低了37.87%。
-
表 1 粗校准和精校准的结果对比
Table 1 Comparison of coarse and fine calibration results
方法 $ \mathrm{\Delta }t $/m $ \mathrm{\Delta }X $/m $ \mathrm{\Delta }Y $/m $ \mathrm{\Delta }Z $/m $ \mathrm{\Delta }\theta $/(°) $ \mathrm{\Delta }R $/(°) $ \mathrm{\Delta }H $/(°) $ \mathrm{\Delta }A $/(°) 粗校准 0.195 0.096 0.124 0.114 0.991 0.929 0.778 0.991 精校准 0.055 0.031 0.028 0.036 0.394 0.257 0.212 0.205 表 2 标定参数扰动实验整体结果
Table 2 Overall results of the perturbation experiments on calibration parameters
参数 平均值 标准差 最大值 最小值 $ \Delta X $ 0.0223 m0.0062 0.0339 m0.0097 m$ \Delta $Y 0.0238 m0.0094 0.0409 m0.0073 m$ \Delta Z $ 0.0210 m0.0062 0.0326 m0.0099 m$ \Delta $R 0.1689 °0.0477 0.2490 °0.0691 °$ \Delta $H 0.1434 °0.0372 0.2132 °0.0578 °$ \Delta $A 0.1371 °0.0389 0.2035 °0.0512 °表 3 不同方法的校正结果对比
Table 3 Comparison of correction results across different methods
方法 平移误差/m 旋转误差/(°) $ \mathrm{\Delta }t $ $ \mathrm{\Delta }X $ $ \mathrm{\Delta }Y $ $ \mathrm{\Delta }Z $ $ \mathrm{\Delta }\theta $ $ \mathrm{\Delta }R $ $ \mathrm{\Delta }H $ $ \mathrm{\Delta }A $ 文献[17] 0.098 0.059 0.064 0.047 0.767 0.445 0.497 0.374 精校准 0.055 0.031 0.028 0.036 0.394 0.257 0.212 0.205 表 4 不同点云输入的消融研究
Table 4 Ablation study on different point cloud inputs
实验设置 $ \mathrm{平}\mathrm{移}\mathrm{误}\mathrm{差}/\mathrm{m} $ $ \mathrm{旋}\mathrm{转}\mathrm{误}\mathrm{差} $/(°) 单帧点云 0.112 0.852 融合帧点云 0.055 0.394 表 5 权重系数的消融研究
Table 5 Ablation study of weight coefficients
实验设置 $ \mathrm{平}\mathrm{移}\mathrm{误}\mathrm{差}/\mathrm{m} $ $ \mathrm{旋}\mathrm{转}\mathrm{误}\mathrm{差} / $(°) 不考虑权重 0.086 0.634 考虑权重 0.055 0.394 -
[1] 王国法. 煤矿智能化最新技术进展与问题探讨[J]. 煤炭科学技术,2022,50(1):1-27. DOI: 10.3969/j.issn.0253-2336.2022.1.mtkxjs202201001 WANG Guofa. New technological progress of coal mine intelligence and its problems[J]. Coal Science and Technology,2022,50(1):1-27. DOI: 10.3969/j.issn.0253-2336.2022.1.mtkxjs202201001
[2] 陈晓晶. 井工煤矿运输系统智能化技术现状及发展趋势[J]. 工矿自动化,2022,48(6):6-14,35. CHEN Xiaojing. Current status and development trend of intelligent technology of underground coal mine transportation system[J]. Journal of Mine Automation,2022,48(6):6-14,35.
[3] 宋秦中,胡华亮. 基于CNN算法的井下无人驾驶无轨胶轮车避障方法[J]. 金属矿山,2023(10):168-174. SONG Qinzhong,HU Hualiang. Obstacle avoidance method for underground unmanned trackless rubber-tyred vehicle based on CNN algorithm[J]. Metal Mine,2023(10):168-174.
[4] 张宏伟,高亚男,王宇,等. 燃料受限条件下矿区无人驾驶卡车路径最优化策略研究[J]. 金属矿山,2024(8):140-145. ZHANG Hongwei,GAO Yanan,WANG Yu,et al. Study on route optimization strategy of unmanned truck in mining area under fuel constraint condition[J]. Metal Mine,2024(8):140-145.
[5] 胡青松,孟春蕾,李世银,等. 矿井无人驾驶环境感知技术研究现状及展望[J]. 工矿自动化,2023,49(6):128-140. HU Qingsong,MENG Chunlei,LI Shiyin,et al. Research status and prospects of perception technology for unmanned mining vehicle driving environment[J]. Journal of Mine Automation,2023,49(6):128-140.
[6] ZHANG Qilong,PLESS R. Extrinsic calibration of a camera and laser range finder (improves camera calibration)[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems,Sendai,2004. DOI: 10.1109/IROS.2004.1389752.
[7] ZHOU Lipu,DENG Zhidong. Extrinsic calibration of a camera and a lidar based on decoupling the rotation from the translation[C]. IEEE Intelligent Vehicles Symposium,Madrid,2012:642-648.
[8] WANG Weimin,SAKURADA K,KAWAGUCHI N. Reflectance intensity assisted automatic and accurate extrinsic calibration of 3D LiDAR and panoramic camera using a printed chessboard[J]. MDPI AG,2017(8). DOI: 10.3390/RS9080851.
[9] SIM S,SOCK J,KWAK K. Indirect correspondence-based robust extrinsic calibration of LiDAR and camera[J]. Sensors,2016,16(6). DOI: 10.3390/s16060933.
[10] LIAO Qinghai,CHEN Zhenyong,LIU Yang,et al. Extrinsic calibration of lidar and camera with polygon[C]. IEEE International Conference on Robotics and Biomimetics,Kuala Lumpur,2018. DOI: 10.1109/ROBIO.2018.8665256.
[11] 徐孝彬,曹晨飞,张磊,等. 基于四面体特征的面阵激光雷达与相机标定方法[J]. 光子学报,2024 ,53(7):176-190. XU Xiaobin,CAO Chenfei,ZHANG Lei,et al. Planar array lidar and camera calibration method based on tetrahedral features[J]. Acta Photonica Sinica,2024,53(7):176-190.
[12] 谢婧婷,蔺小虎,王甫红,等. 一种点线面约束的激光雷达和相机标定方法[J]. 武汉大学学报(信息科学版),2021,46(12):1916-1923. XIE Jingting,LIN Xiaohu,WANG Fuhong,et al. Extrinsic calibration method for LiDAR and camera with joint point-line-plane constraints[J]. Geomatics and Information Science of Wuhan University,2021,46(12):1916-1923.
[13] PANDEY G,MCBRIDE J R,SAVARESE S,et al. Automatic extrinsic calibration of vision and lidar by maximizing mutual information[J]. Journal of Field Robotics,2015,32(5):696-722. DOI: 10.1002/rob.21542
[14] ZHAO Yipu,WANG Yuanfang,TSAI Y. 2D-image to 3D-range registration in urban environments via scene categorization and combination of similarity measurements[C]. IEEE International Conference on Robotics and Automation ,Stockholm,2016:1866-1872.
[15] JIANG Peng,OSTEEN P,SARIPALLI S. SemCal:semantic LiDAR-camera calibration using neural mutual information estimator[C]. IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems,Karlsruhe,2021. DOI: 10.48550/arXiv.2109.10270.
[16] MA Tao,LIU Zhizheng,YAN Guohang,et al. CRLF:automatic calibration and refinement based on line feature for LiDAR and camera in road scenes[EB/OL]. (2021-03-08)[2024-06-22]. https://arxiv.org/abs/2103.04558v1.
[17] ZHU Yufeng,LI Chenghui,ZHANG Yubo. Online camera-LiDAR calibration with sensor semantic information[C]. IEEE International Conference on Robotics and Automation,Paris,2020. DOI: 10.1109/ICRA40945.2020.9196627.
[18] ISHIKAWA R,OISHI T,IKEUCHI K. LiDAR and camera calibration using motions estimated by sensor fusion odometry[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems,Madrid,2018:7342-7349.
[19] WANG Li,XIAO Zhipeng,ZHAO Dawei,et al. Automatic extrinsic calibration of monocular camera and LIDAR in natural scenes[C]. IEEE International Conference on Information and Automation,Wuyishan,2018:997-1002.
[20] SCHNEIDER N,PIEWAK F,STILLER C,et al. RegNet:multimodal sensor registration using deep neural networks[C]. IEEE Intelligent Vehicles Symposium,Los Angeles,2017:1803-1810.
[21] IYER G,RAM R K,MURTHY J K,et al. CalibNet:geometrically supervised extrinsic calibration using 3D spatial transformer networks[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems,Madrid,2018:1110-1117.
[22] LYU Xudong,WANG Shuo,YE Dong. CFNet:lidar-camera registration using calibration flow network[J]. Sensors,2021. DOI: 10.48550/arXiv.2104.11907.
[23] WANG Weimin,NOBUHARA S,NAKAMURA R,et al. SOIC:semantic online initialization and calibration for LiDAR and camera[EB/OL]. (2023-03-09)[2024-06-22]. https://arxiv.org/abs/2003.04260v1.
[24] JAIN J,LI Jiachen,CHIU M,et al. OneFormer:one transformer to rule universal image segmentation[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition,Vancouver,2023:2989-2998.
[25] XIAO Zeqi,ZHANG Wenwei,WANG Tai,et al. Position-guided point cloud panoptic segmentation transformer[EB/OL]. (2023-03-23)[2024-06-22]. https://arxiv.org/abs/2303.13509v1.



 下载:
下载: