Review of discharge theory and numerical research on intrinsically safe low voltage DC circuits
-
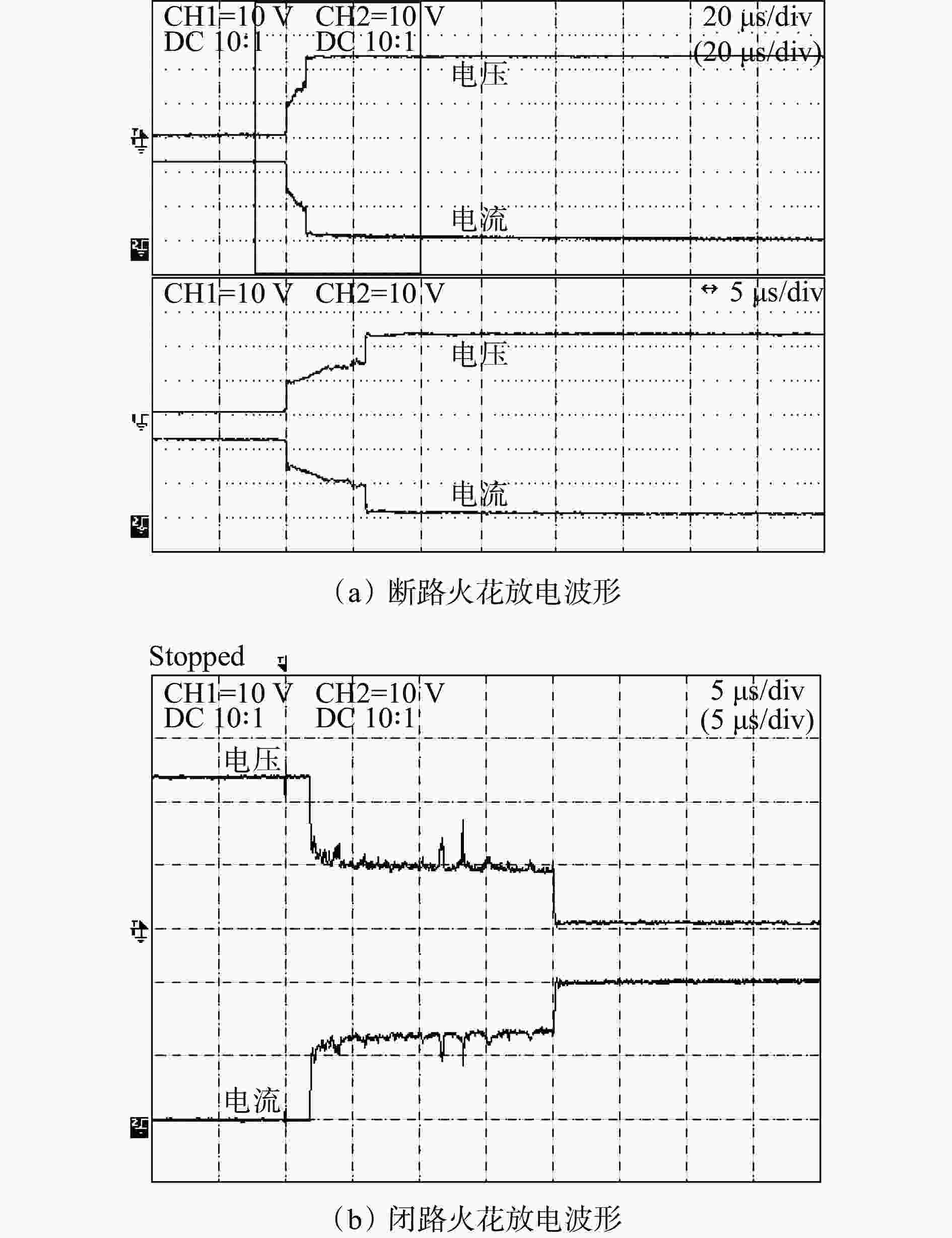
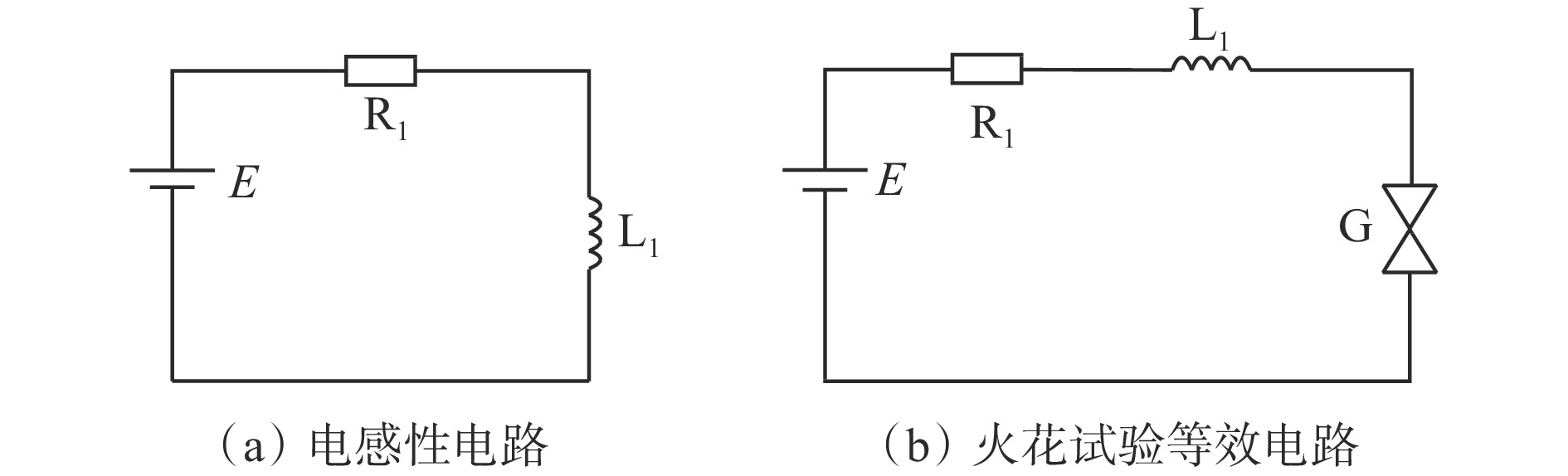
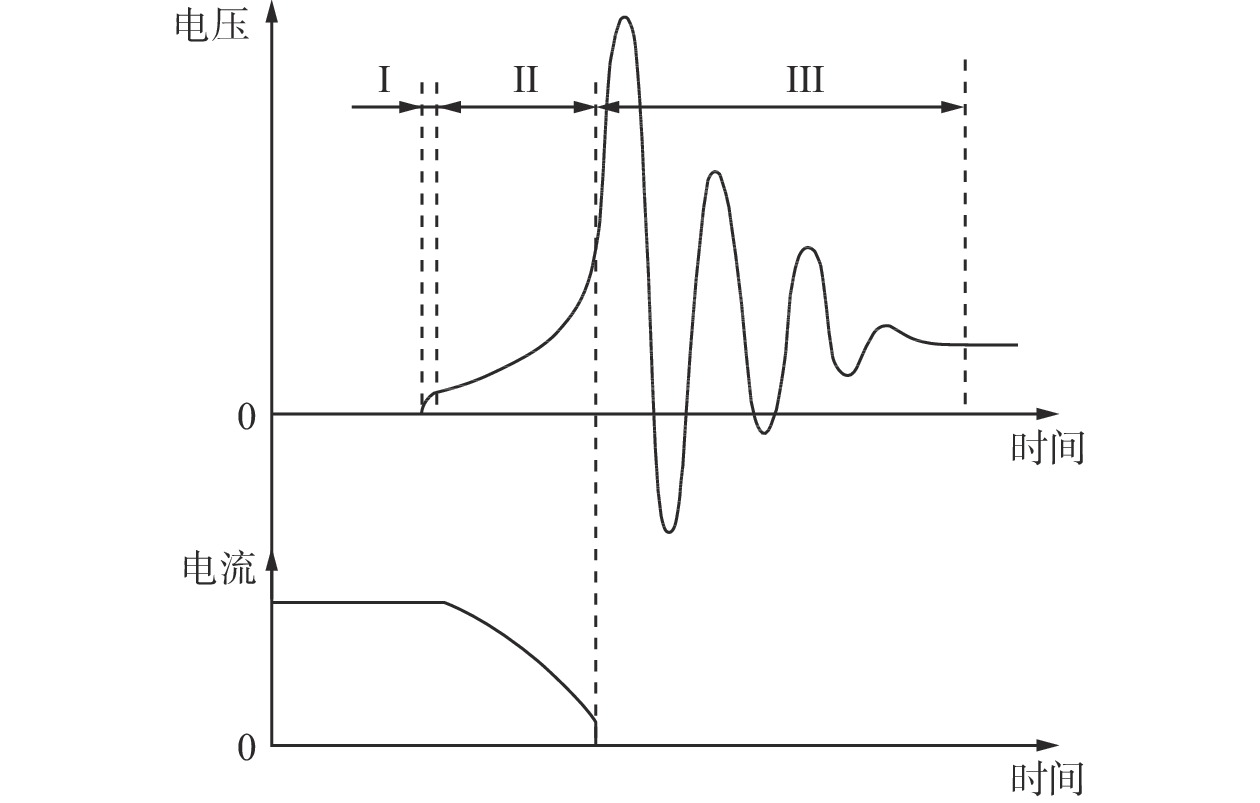
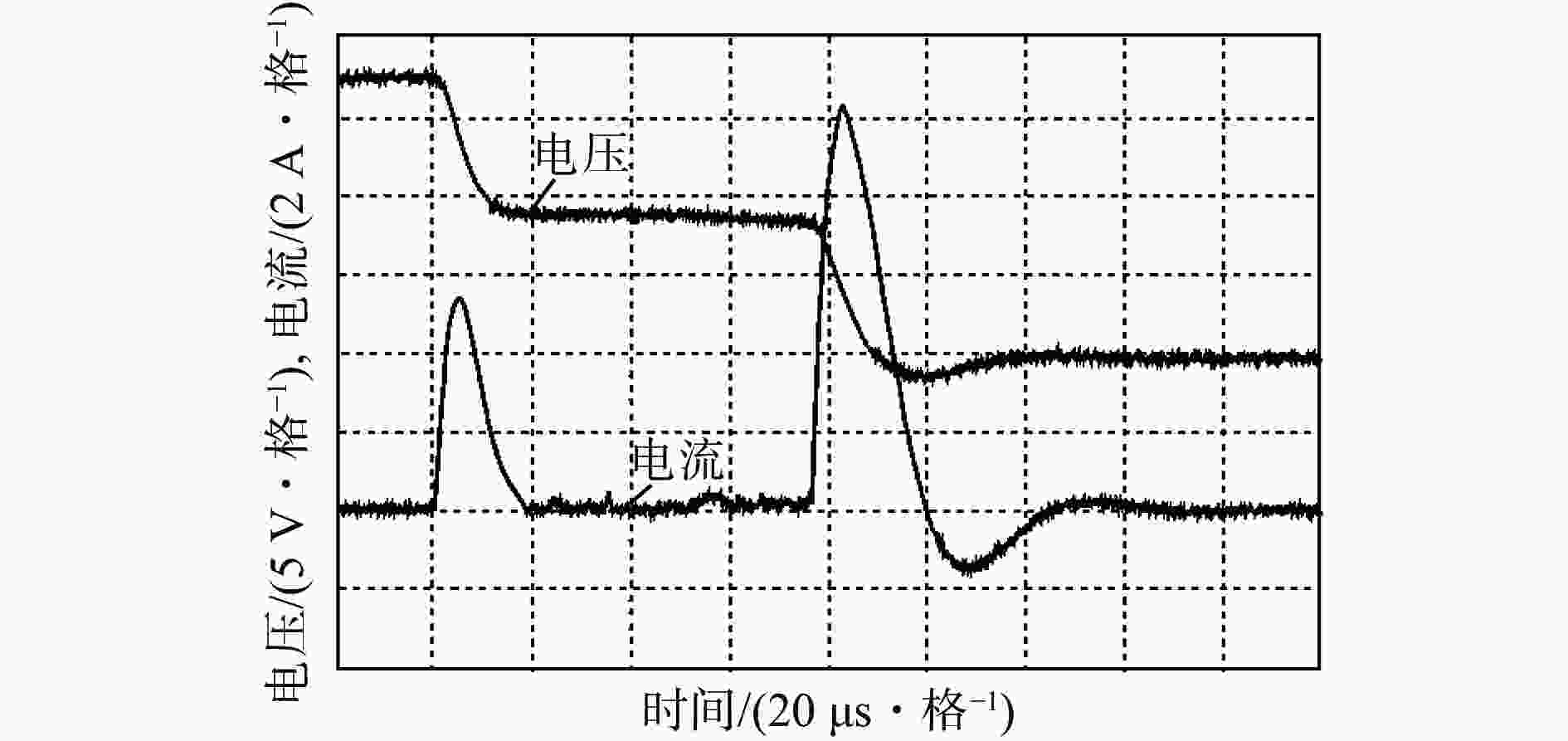
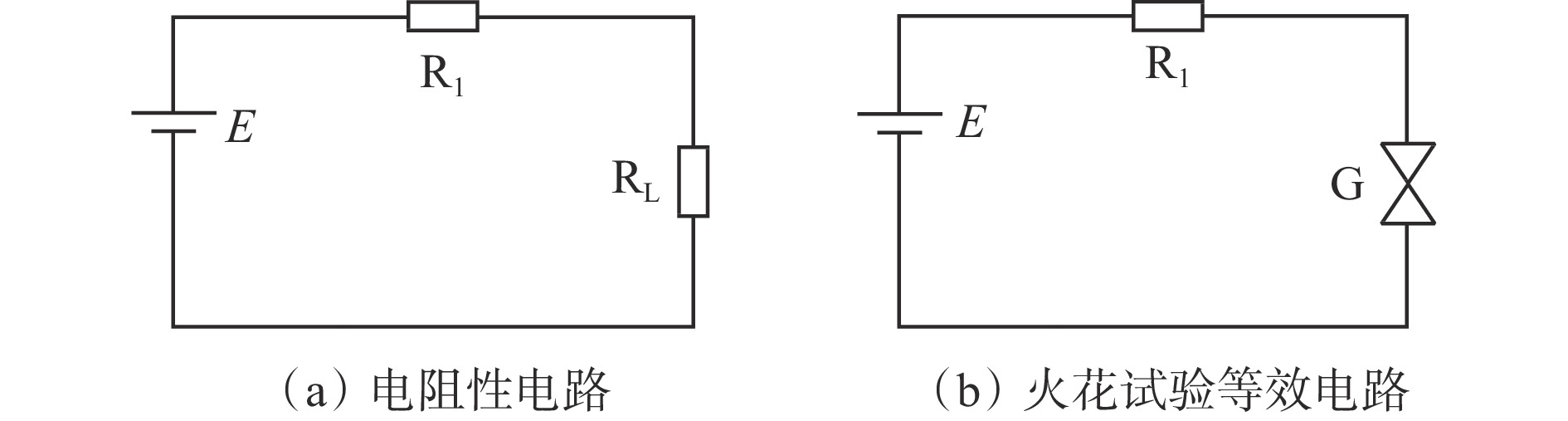
摘要: 分析了本质安全电阻性、电感性和电容性电路的放电特性，指出电感性、电容性电路放电能量较大，且放电波形较复杂，而电阻性电路放电特性相对简单。总结了本质安全电感性电路和电容性电路放电机理及其放电数学模型研究现状，给出了放电电流线性衰减模型、放电电流抛物线模型、静态伏安特性模型、动态伏安特性模型、电弧电阻指数模型等的数学表达式。介绍了宏观及微观气体放电数值模拟方法的优缺点：宏观方法计算量小，但只能仿真气体放电的外部特性；微观方法计算量大，但能精确仿真放电过程中各粒子的运动特性。探究了直流放电电路和放电电弧的微观机理，得出了不同电极材料、不同电极间距及不同初始电气参数下，不同表面发射机理如热场致电子发射、场致发射等对气体放电的影响。针对研究现状，提出了本质安全直流电路放电研究需进一步解决的问题：① 宏观试验−数学模型表达式复杂、计算量大，部分模型适用范围单一，无法真正实现本质安全电路非爆炸评估。 ② 本质安全电路放电的研究大部分还是基于IEC火花放电装置，影响特定电路参数放电的研究。③ 放电电弧的数值仿真研究无法定量研究两电极接触分断过程的电弧形成机理。④ 针对电感性电路、电容性电路的电感、电容对放电电弧特性的影响，还没有更具说服力的研究成果。⑤ 目前对于电路断路电弧或短路火花如何引爆危险气体的理论研究较少。Abstract: The discharge characteristics of intrinsically safe resistive, inductive and capacitive circuits are analyzed. It is pointed out that inductive and capacitive circuits have larger discharge energy and more complex discharge waveforms. The resistive circuits have relatively simple discharge characteristics. The discharge mechanism and mathematical models of the intrinsically safe inductive and capacitive circuits are summarized. The mathematical expressions of different models, such as linear decay model of discharge current, parabolic model of discharge current, static volt-ampere characteristic model, dynamic volt-ampere characteristic model and arc resistance index model, are given. The advantages and disadvantages of the numerical simulation method of macroscopic and microscopic gas discharge are introduced. The macroscopic methods have a small amount of calculation, but it can only simulate the external characteristics of gas discharge. The microscopic methods have a large amount of calculation, but it can accurately simulate the motion characteristics of particles in the discharge process. The microcosmic mechanism of the DC discharge circuit and discharge arc is studied. Under different electrode materials, different electrode distances and different initial electrical parameters, the influence of different surface emission mechanisms such as thermal field emission and field emission on gas discharge is obtained. According to the current research situation, the problems that need to be solved in the discharge research of intrinsically safe DC circuits are put forward. ① The macro experiment-mathematical model has complex expression and a large amount of calculation. Some models have a single scope of application and cannot truly achieve the non-explosive evaluation of intrinsically safe circuits. ② Most of the research on discharge in intrinsically safe circuits is based on IEC spark discharge devices, which affects the discharge of specific circuit parameters. ③ The numerical simulation of discharge arc cannot quantitatively study the arc formation mechanism during the contact breaking process of two electrodes. ④ There are no more convincing research results on the influence of inductance and capacitance of the inductive circuit and capacitive circuit on the characteristics of discharge arc. ⑤ At present, there are few theoretical studies on how to ignite dangerous gases by electric arc due to circuit break arc or short circuit spark.
-
图 7 高速摄像机拍摄的电阻性电路和电感性电路放电电弧
Figure 7. Discharge arc of resistive circuit and inductive circuit captured by a high-speed camera
图 8 钨丝表面晶须及放电光谱
Figure 8. Whisker and discharge spectrum on the surface of tungsten wire
图 11 激发温度和由电导率确定的温度在不同电流下的比较（50，60，100 mA点燃,电压30 V）
Figure 11. Comparison of excitation temperature and temperature determined by discharge conductivity at different current values (50，60，100 mA ignition, voltage 30 V)
图 12 激发温度与由电导率确定的温度比较（60 mA点燃，电压30 V）
Figure 12. Comparison of excitation temperature and temperature determined by conductivity (60 mA ignition, voltage 30 V)
表 1 电感性电路放电模型数学表达式
Table 1. Mathematical expression of inductive circuit discharge model
文献 模型表达式 各参数含义 文献[6] 静态伏安特性方程：
${V}_{{\rm{g}}}=K\left({l}_{0}+vt\right){I}_{{\rm{g}}}^{-\delta }+{V}_{{\rm{a}}}$
通过基尔霍夫电压方程变换并计算得$L\dfrac{ {\rm{d} } }{ {\rm{d} }t}{i}_{ {\rm{g} } }\left(t\right)+R{i}_{ {\rm{g} } }\left(t\right)+ \\ 8\;085\left({l}_{0}+25t\right){i}_{{\rm{g}}}^{-0.68}\left(t\right)+8.6={V}_{0}$${V}_{{\rm{g}}}$：放电电压
$ K $：常数系数
$ {l}_{0} $：初始放电间隙
$ v $：电极分离速度
$ t $：放电时间
${I}_{{\rm{g}}}$：放电电流
δ：常数系数
${V}_{{\rm{a}}}$：电弧阴极电位降
$ L $：电感
R：电路总电阻
${i}_{{\rm{g}}}$：电弧电流
$ {V}_{0} $：电源电压文献[11] 线性衰减模型：
放电电流：${i}_{{\rm{g}}}=I\left(1-\dfrac{t}{T}\right)$
放电电压：${u}_{{\rm{g}}}=\dfrac{E}{T}\left(t+\dfrac{L}{R}\right)$
放电时间：${T}=\dfrac{LI}{ {V}_{ {\rm{arc} }{\rm{min} } } }$${i}_{{\rm{g}}}$：电弧电流
$ I $：稳定电流值
${t}$：放电时间
$ T $：计算放电时间
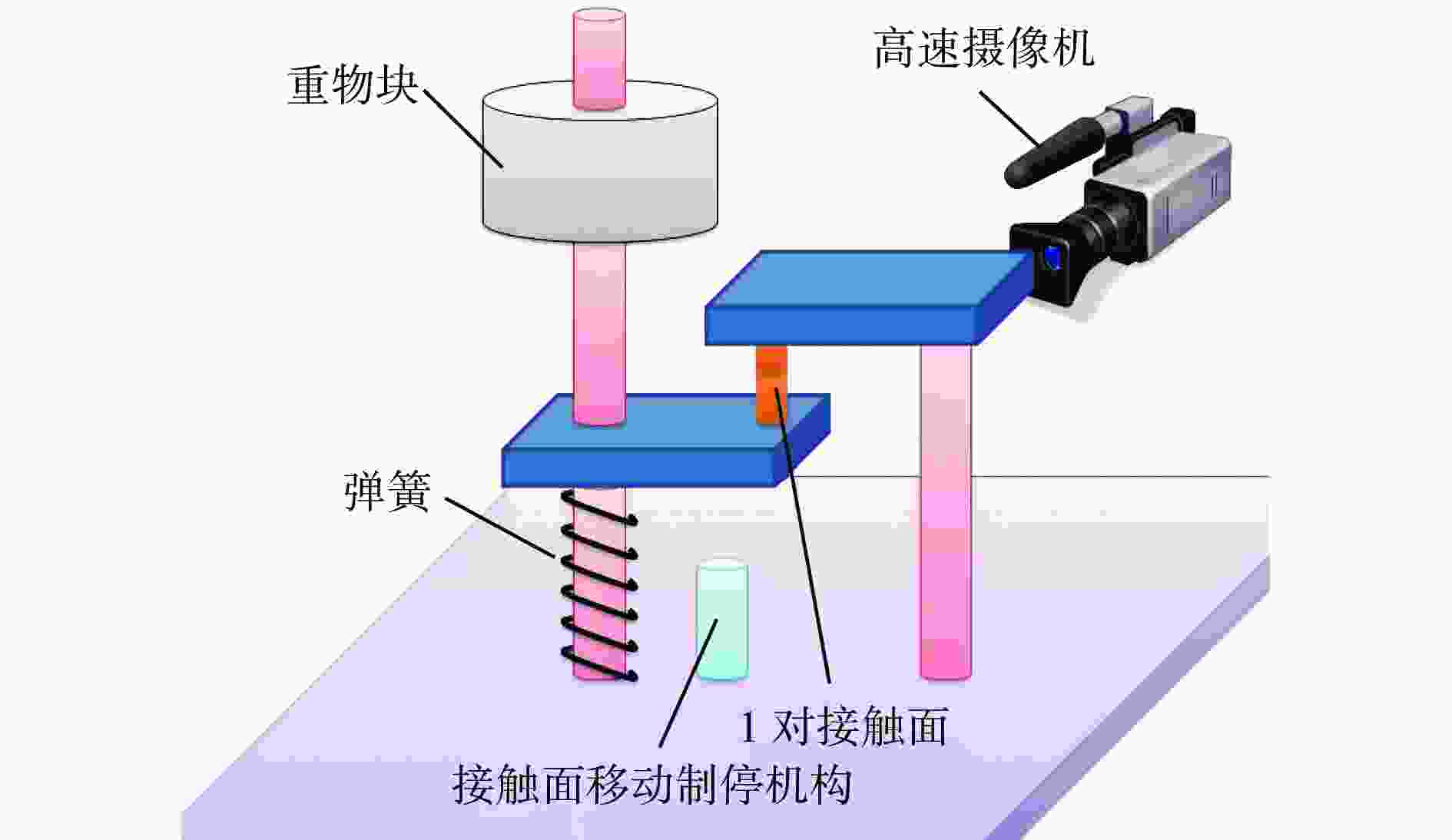
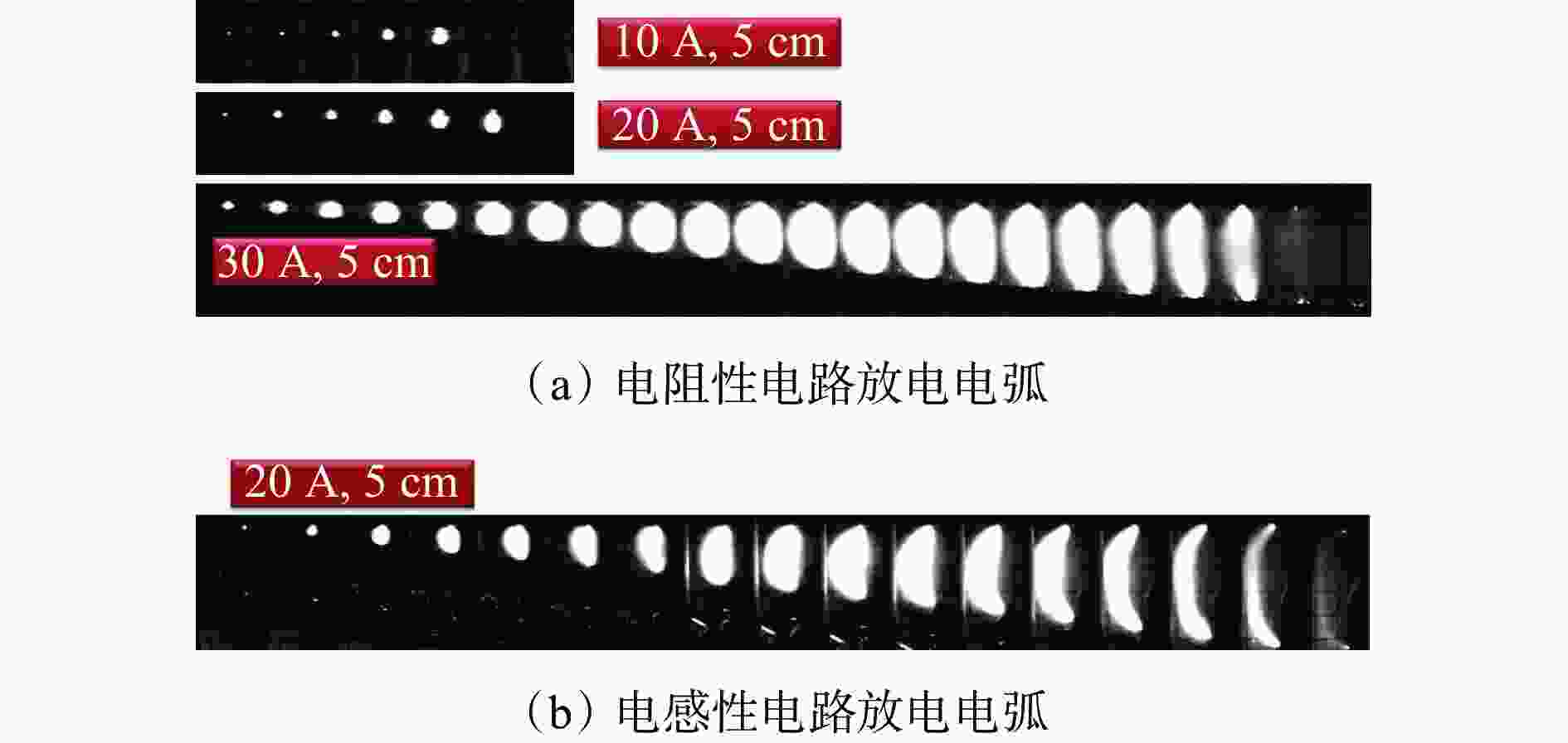
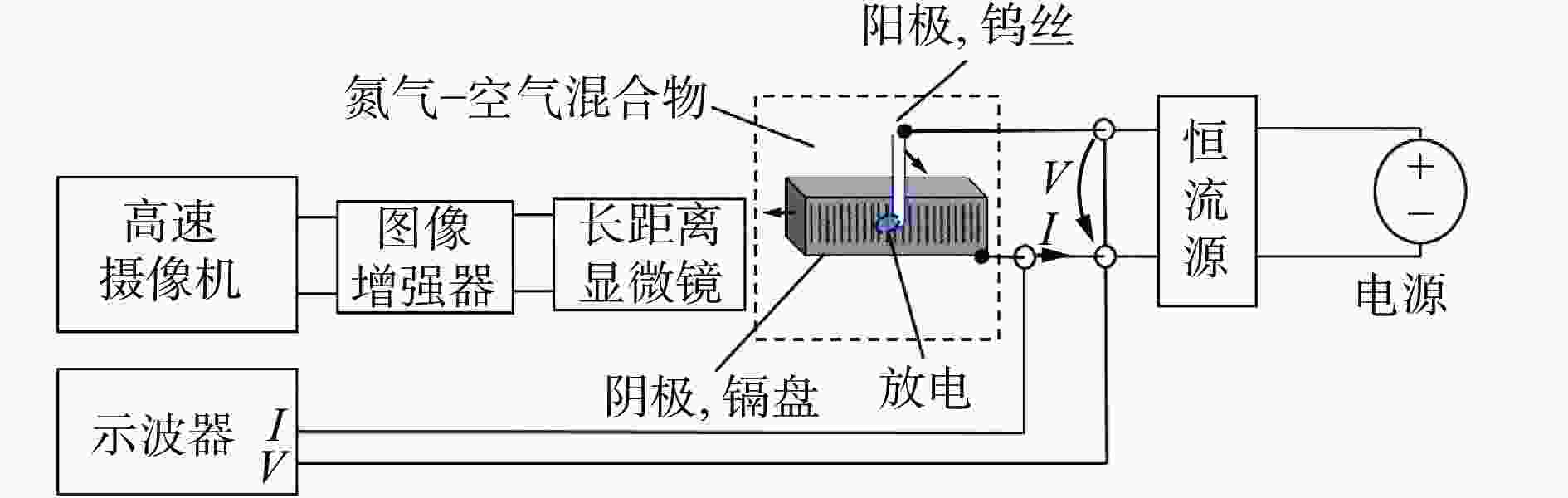
${u}_{{\rm{g}}}$：放电电压
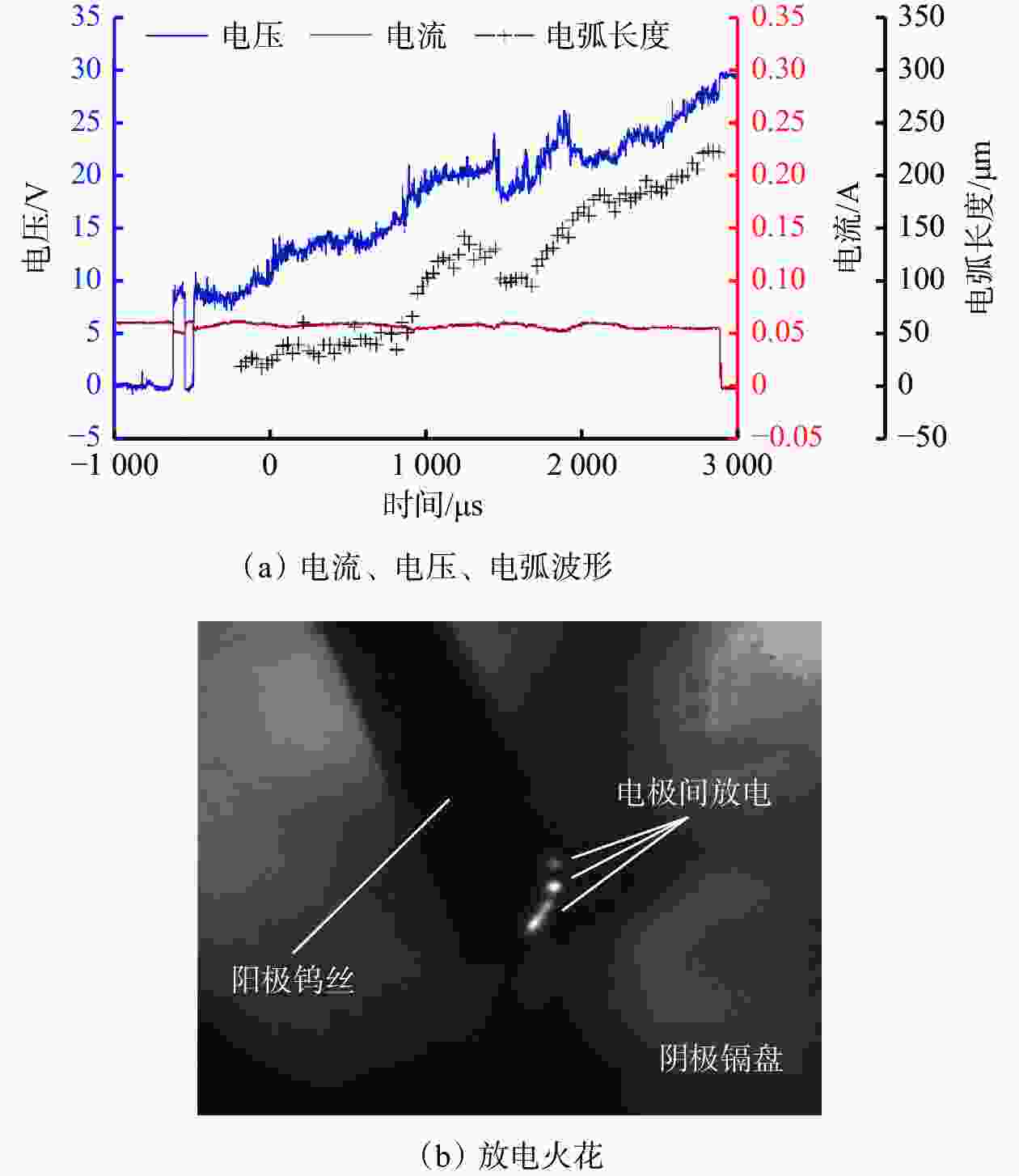
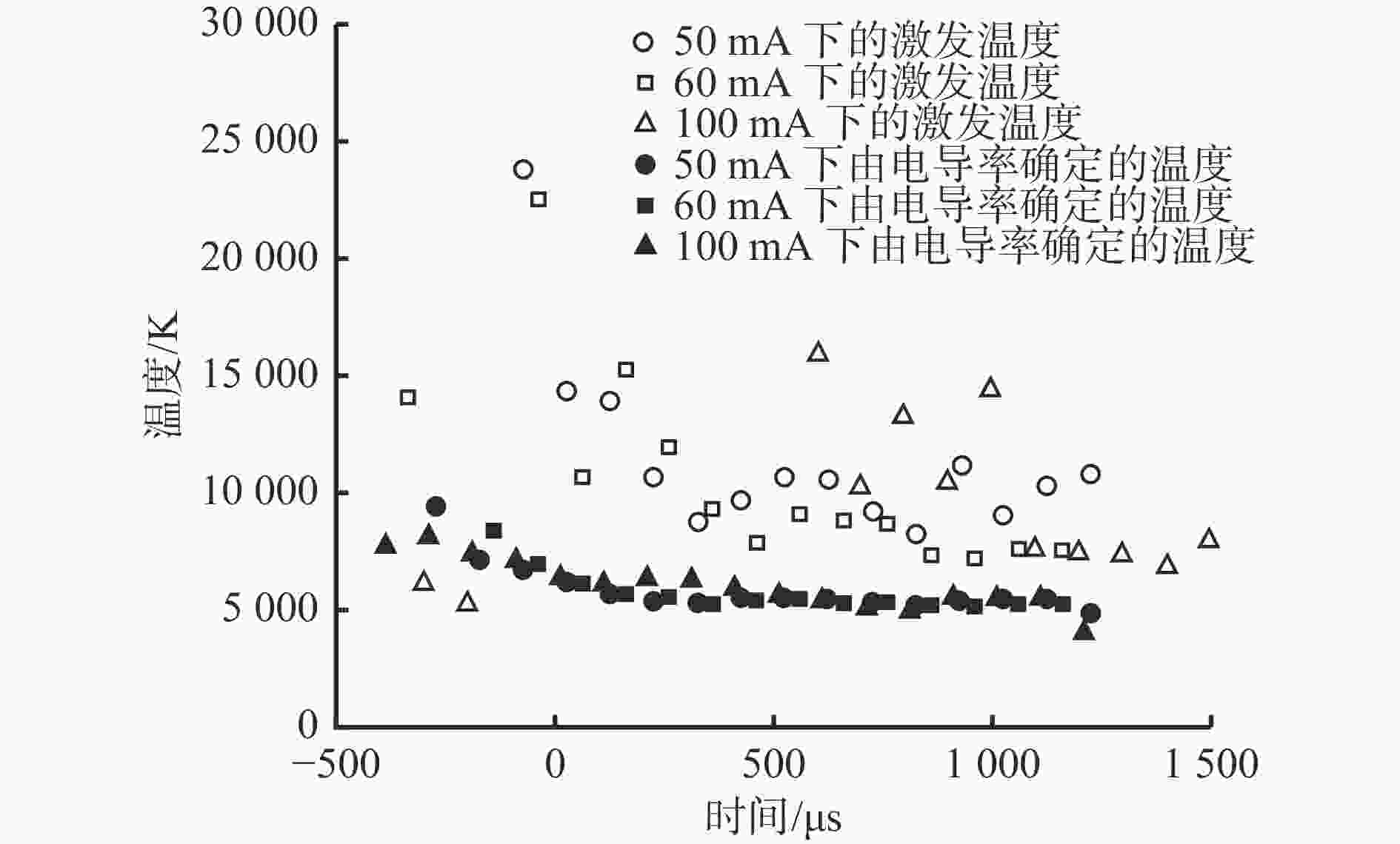
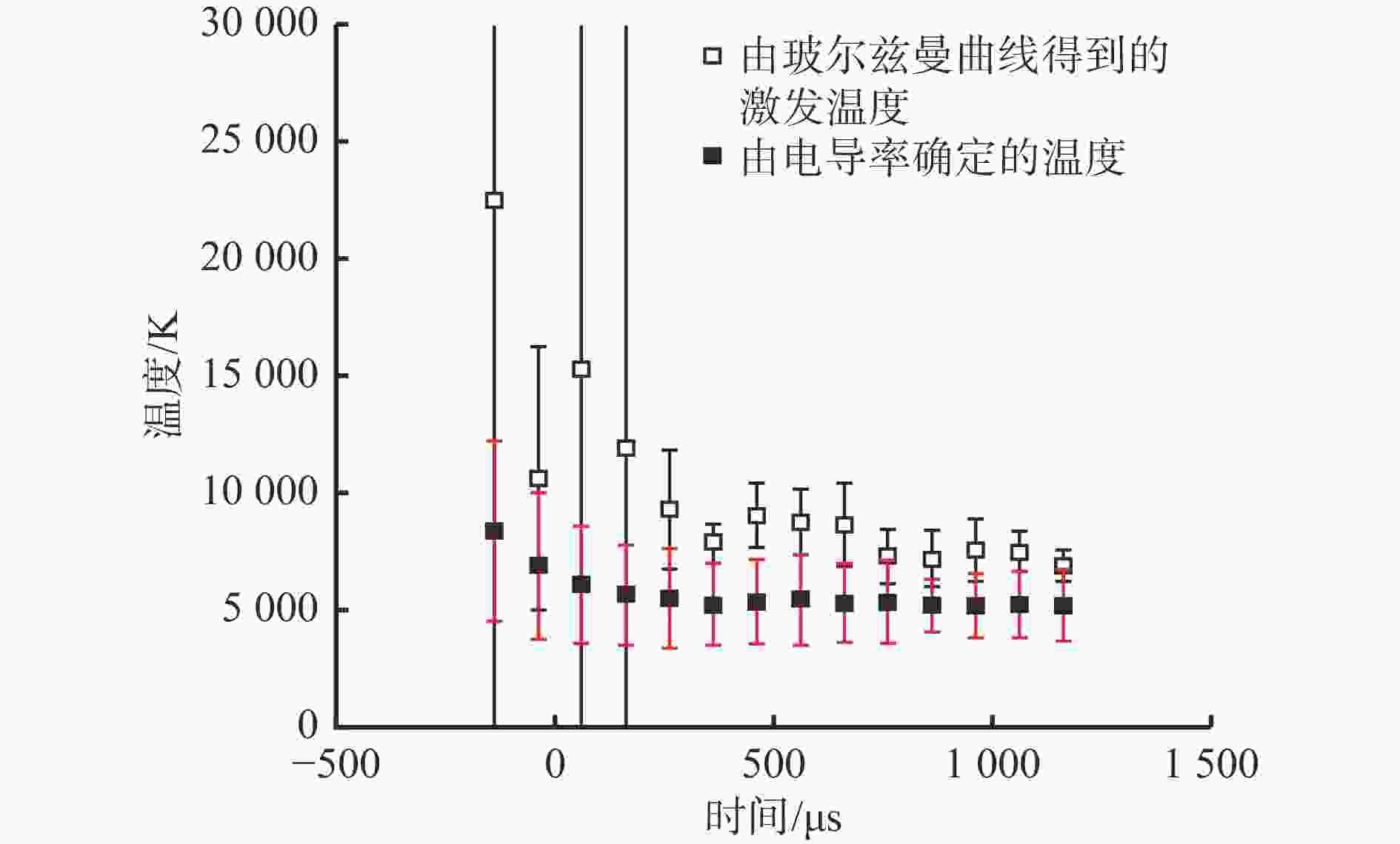
$ E $：电源电势
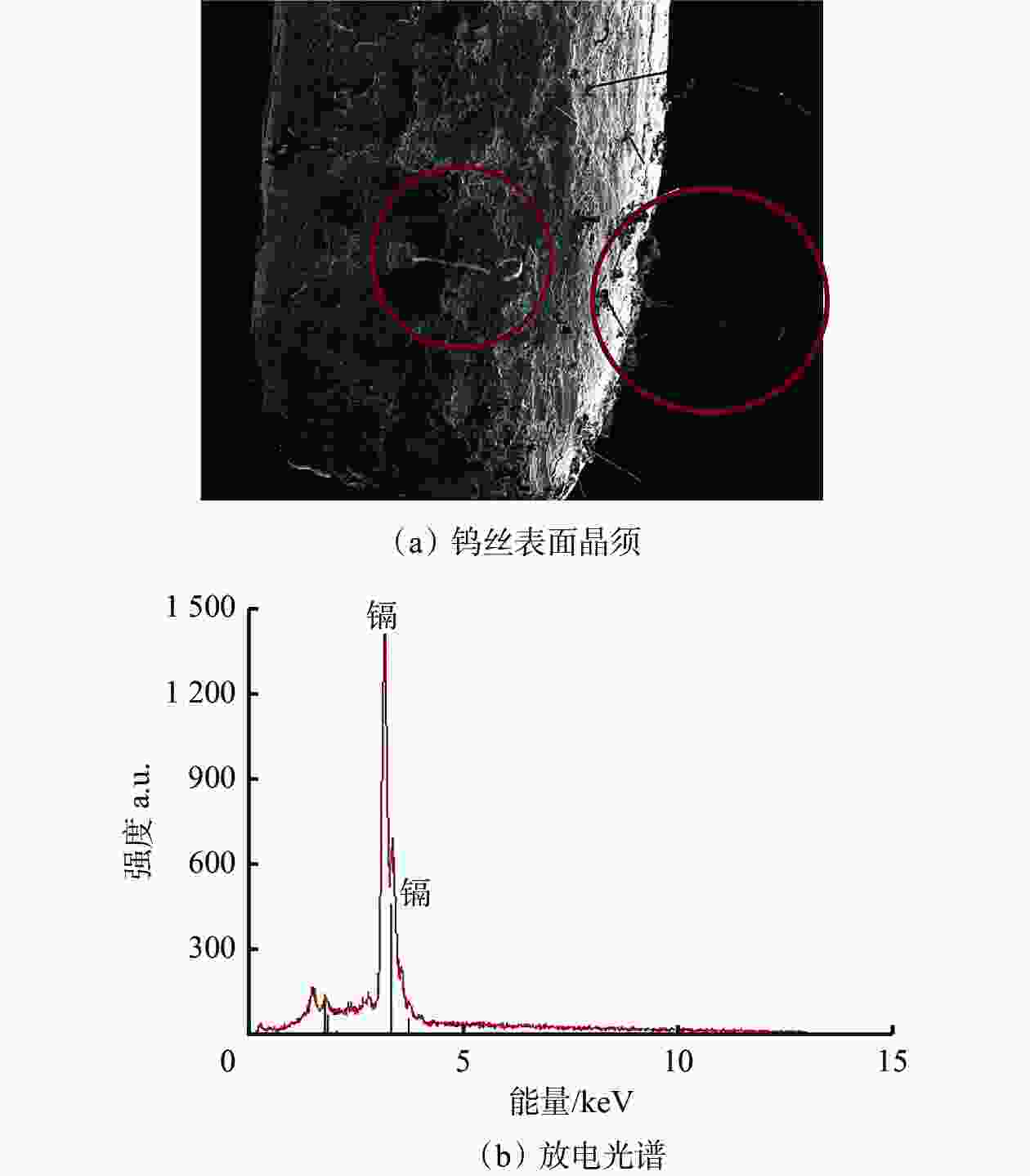
L：电感
$ R $：电路总电阻
$ {V}_{{\rm{arc}}{\rm{min}}} $：最小建弧电压文献[12] 动态伏安特性方程：${V}_{{\rm{g}}}={V}_{ {\rm{max} } }+\dfrac{ {V}_{ {\rm{max} } }-{V}_{ {\rm{min} } } }{I}{i}_{{\rm{g}}}$
电弧电阻表达式：${R}_{ {\rm{g} } }=\dfrac{ {V}_{ {\rm{min} } } }{I} \dfrac{E-\left({V}_{ {\rm{max} } }-{V}_{ {\rm{min} } }\right){ {\rm{exp} } }{\left(-\dfrac{t}{f} \right)} }{E-{V}_{ {\rm{max} } }+{V}_{ {\rm{min} } }{ {\rm{exp} } }{\left(-\dfrac{t}{f} \right)} }$
$ f=\dfrac{IL}{E-\left({V}_{{\rm{max}}}-{V}_{{\rm{min}}}\right)} $$V_{\rm{g}}$ ：放电电压
$V_{{{\rm{max}}}} $：放电终止电压
$V_{\rm{{\rm{min}}}} $：放电初始电压
I：稳定电流值
$i_{\rm{g}} $：电弧电流
$R_{\rm{g}} $：电弧电阻
E：电源电压
$ t $：放电时间
f：时间常数
L：电感文献[14] 放电终止电压：$ {V}_{{\rm{max}}}={V}_{{\rm{arc}}{\rm{min}}}+\left(39+13L\right)I $
电弧电流、电压表达式：${i}_{ {\rm{g} } }=I-\dfrac{ {V}_{ {\rm{arc} }{\rm{min} } } }{R-\left(39+13L\right)}\left[1-{ {\rm{exp} } }{ \left( \dfrac{R-\left(39+13L\right)}{L}t \right)}\right]$
${V}_{ {\rm{g} } }=\dfrac{ {V}_{ {\rm{arc} }{\rm{min} } } }{R- \left( 39+13L\right)}\left[ R-\left(39+13L\right) { {\rm{exp} } }{\left( -\dfrac{R-\left(39+13L\right)}{L}t \right) }\right]$
电弧电阻表达式：${r}_{{\rm{g}}}=\dfrac{ {V}_{ {\rm{arc} }{\rm{min} } }+\left(39+13L\right)I}{ {i}_{{\rm{g}}} }-\left(39+13L\right)$$ {V}_{{\rm{max}}} $：放电终止电压
$ {V}_{{\rm{arc}}{\rm{min}}} $：最小建弧电压
$ L $：电感
$ I $：稳定电流值
${i}_{{\rm{g}}}$：电弧电流
$ R $：电路总电阻
$ t $：放电时间
${V}_{{\rm{g}}}$：放电电压
${r}_{{\rm{g}}}$：电弧电阻文献[15] 电极分离速度表达式：${v}^{ {'} } \left(t\right) \approx 25+1\; 940\mathrm{sin}\left(\dfrac{ {\text{π} } }{730}t\right)$
电弧长度表达式：$l={l}_{0}+25\times {10}^{-6}t+0.45\left[1-\mathrm{cos}\left(\dfrac{{\text{π}} }{730}t\right)\right]$
动态伏安表达式：${V}_{ {\rm{g} } }=K{i}_{ {\rm{g} } }^{-\delta }\left\{ { {l}_{0}+25\times {10}^{-6}t+0.45\left[1-\mathrm{cos}\left(\dfrac{ {\text{π} } }{730}t\right)\right] } \right\}+{V}_{ {\rm{a} } }$
电弧电阻表达式： $ \begin{array}{l}{r}_{ {\rm{g} } }=\dfrac{ {V}_{ {\rm{g} } } }{ {i}_{ {\rm{g} } } }=\dfrac{9.45}{ {i}_{ {\rm{g} } } }+ 4 \; 500 \bigg\{ {l}_{0}+25\times {10}^{-6}t+ \\ \;\;\;\;\;\;\;\; 0.45\left[1-\mathrm{cos}\left(\dfrac{ {\text{π} } }{730}t\right)\right] \bigg\}{I}_{ {\rm{g} } }^{-1.6} \end{array}$$ {v}^{{'}} \left(t\right) $：电弧分离速度
$ t $：放电时间
$ l $：电弧长度
$ {l}_{0} $：初始放电间隙
${V}_{{\rm{g}}}$：放电电压
K：常数系数
${i}_{{\rm{g}}}$：电弧电流
$ \delta $：常数系数
${V}_{{\rm{a}}}$：电弧阴极电位降
rg：电弧电阻文献[18] 简单电感性电路放电时间表达式：$T={T}_{ {\rm{R} } }+{T}_{ {\rm{L} } }={d}_{ {\rm{R} }{\rm{max} } }{v}^{-{k}_{1} }+{d}_{ {\rm{L} }{\rm{max} } }{ {\rm{exp} } }{\left(-\dfrac{v}{ {k}_{2} } \right) }+{T}_{\infty }$
电弧等效时变电阻表达式：${R}_{ {\rm{arc} } }=\dfrac{v t}{a{t}^{2}+bt+c}$
利用莱文贝格−马夸特优化算法进行拟合，得到上式中参数值${T}_{{\rm{R}}}$：电阻电路放电时间
${T}_{{\rm{L}}}$：电感电弧放电时间
${d}_{{\rm{R}}{\rm{max} } }$：电阻电弧长度
${d}_{{\rm{L}}{\rm{max} } }$：电感电弧长度
$ v $：放电电弧电压
k1,k2：特征系数
$T_ {{\infty}}$：电弧放电时间稳
定值
a,b,c：极间电阻特征
参数
t：放电时间文献[20] 电感性电路简单放电数学模型：$v\left(i,l\right)={V}_{{\rm{f}}}+\alpha l\left(1+\dfrac{\beta }{ {i}^{n} }\right)$
恒定电弧长度拟合函数：$V\left(i\right)=13.16+\dfrac{3.077}{{i}^{0.296}} $
恒定放电电流拟合函数：$ V\left(l\right)=9.8+40.93l $
联合上式可得电感性电路简单模型数学表达式：$ v\left(i,l\right)=9.8+18.6l\left(1+\dfrac{0.914}{{i}^{0.296}}\right) $$ v $：放电电弧电压
$ i $：放电电弧电流
$ l $：放电电弧长度
${V}_{{\rm{f}}}$：阴极电压降
$ \alpha $，β，n：拟合参数
下载: 导出CSV
表 2 电容性电路放电模型数学表达式
Table 2. Mathematical expression of capacitive circuit discharge model
文献 模型表达式 各参数含义 文献[22] 电容性电路有触点短路放电数学模型：
当0≤t≤2.35+1.02C时：$\left\{ \begin{array}{l}{u}_{\rm c}\left(t\right)={V}_{\rm i}{ {\rm{exp} } }{(t\alpha) }\\ {i}_{\rm c}\left(t\right)=-{V}_{\rm i}{C\alpha {\rm{exp} } }{(t\alpha )}\end{array}\right.$
当2.35+1.02C≤t≤4.04+7.35C时：$\left\{ \begin{array}{l}{u}_{\rm c}\left(t\right)={V}_{\rm H}\\ {i}_{\rm c}\left(t\right)=-{\alpha C{V}_{\rm H}{\rm{exp} } }{\left[\alpha \left(T-2.35-1.02\mathrm{C}\right)\right]}\end{array}\right.$
当t＞4.04+7.35C时：$\left\{ \begin{array}{l}{u}_{\rm c}\left(t\right)={V}_{\rm H}{ {\rm{exp} } }{(\beta) }\\ {i}_{\rm c}\left(t\right)=\dfrac{ {V}_{\rm H} }{ {R}_{\rm 3} }{ {\rm{exp} } }{(\beta) }\end{array}\right.$
$\alpha =\dfrac{{\rm{ln}}\left({V}_{\rm H}/{V}_{\rm i}\right)}{2.35+1.02C}，\beta =\dfrac{4.04+7.35C-t}{ {R}_{\rm 3}C}$$ t $：放电时间
$ C $：电路电容
$ {u}_{\rm c} $：电容电压
$ {i}_{\rm c} $：电容电流
$ {V}_{\rm i} $：初始电压
$ {V}_{\rm H} $：放电维持电压
$ T：\mathrm{计}\mathrm{算}\mathrm{放}\mathrm{电}\mathrm{时}\mathrm{间} $
R3：两电极闭合后放
电回路总电阻
$\alpha ， \beta $：拟合参数文献[23] 电容性电路指数模型：
放电电流：
${i}_{\rm g}=\dfrac{E-{u}_{\rm T} }{ {R}^{2}C\left[1-{ {\rm{exp} } }{\left(-\dfrac{1}{RC}T\right)}\right]}t{\; {\rm{exp} } }{\left(-\tfrac{1}{RC}t\right)}$
放电电压：${u}_{\rm g}=\dfrac{ {u}_{\rm T}-E{ {\rm{exp} } }{\left(-\dfrac{1}{RC}T \right)} }{1-{ {\rm{exp} } }{\left(-\dfrac{1}{RC}T \right)} }+\dfrac{ {E-u}_{\rm T} }{1-{ {\rm{exp} } }{\left(-\dfrac{1}{RC}T \right)} }{ {\rm{exp} } }{\left(-\dfrac{1}{RC}t \right)}$$ E $：电源电压
$ {u}_{\rm T} $：每次放电结束时
的放电电压
$ R $：电路总电阻
$ C $：电路电容
$ T：\mathrm{计}\mathrm{算}\mathrm{放}\mathrm{电}\mathrm{时}\mathrm{间} $
$ t $：放电时间文献[24] 截止型保护方式下电容性电路放电模型：
放电电压：$ {u}_{\rm g}={U}_{\rm h} $
放电电流：${i}_{\rm g}=\dfrac{E-{U}_{\rm h} }{R}{ {\rm{exp} } }{\left(-\dfrac{1}{RC}t \right)}$$ {U}_{\rm h}：\mathrm{最}\mathrm{小}\mathrm{建}\mathrm{弧}\mathrm{电}\mathrm{压} $
$ E $：电源电压
$ R $：电路总电阻
$ C $：电路电容
$ t $：放电时间
下载: 导出CSV
表 3 气体放电数值仿真模型表达式
Table 3. Expressions of numerical simulation models of gas discharge
文献 模型表达式 各参数含义 文献[31] 空间电子运动：$m\dfrac{ {\rm{d} }{\boldsymbol{x}}}{ {\rm{d} }t}=qE$
电子发射电流密度：
${J}_{{\rm{TFE}}}=e{ \displaystyle \int }_{-\infty }^{\infty }N\left(W\right)D\left(W\right){\rm{d} }W$
其中：
$N\left(W\right)=\dfrac{4 {\text{π}} mkT}{ {h}^{3} }{\rm{ln}}\left[1+{\rm{exp} }\left(-\dfrac{\left(W-{E}_{{\rm{F}}}\right)}{kT}\right)\right]$
$D\left(W\right)= \\ \qquad {\rm{exp} }\left(-2{ \displaystyle \int }_{ {x}_{1} }^{ {x}_{2} }\sqrt{\dfrac{8{ {\text{π} } }^{2} }{ {h}^{2} }\left(\left|W\right|-\dfrac{ {e}^{2} }{16{\text{π} } { {\textit{ε}} }_{0}{\boldsymbol{x} } }-eE{\boldsymbol{x} }\right){\rm{d} }{\boldsymbol{x} } }\right)$m：电子质量
x：电子位移矢量
t：时间
q：电荷量
E：电场强度
e：电子电荷量
W：阴极发射材料
逸出功
k：玻尔兹曼常数
T：温度
h：普朗克常数
EF：阴极表面电场
$ {x}_{1}\mathrm{，}{x}_{2} $：电子位置
$ { {\textit{ε}} }_{0} $：真空介电常数文献[33] MHD模型基本方程组
质量守恒方程：$ \dfrac{\partial \rho }{\partial t}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\rho v\right)=0 $
动量守恒方程：
$\begin{array}{l}\dfrac{\partial \rho { {\boldsymbol{v} } }_{i} }{\partial t}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\rho v{ {\boldsymbol{v} } }_{i}\right)=-\dfrac{\partial p}{\partial {x}_{i} }+ \\ \qquad \displaystyle \sum _{k=1}^{2}\dfrac{\partial }{\partial {x}_{k} }\left[\eta \left(\dfrac{\partial { {\boldsymbol{v} } }_{i} }{\partial {x}_{k} }+\dfrac{\partial { {\boldsymbol{v} } }_{k} }{\partial { {\boldsymbol{v} } }_{i} }+{\left(J\times B\right)}_{i}\right)\right]\end{array}$
能量守恒方程：$\begin{array}{l}\dfrac{\partial \left(\rho H\right)}{\partial t}+\mathrm{d}\mathrm{i}\mathrm{v}\left(\rho {\boldsymbol{v}}H\right)-{\rm{div} }\left[\lambda {\rm{grad}}\left(T\right)\right]= \\ \qquad \dfrac{\partial p}{\partial t}-{S}_{ {\rm{R}}}+\dfrac{ {J}^{2} }{\sigma } \end{array}$
（4）电场方程：${E}_{{\rm{arc}}}\left(t\right)=I\left(t\right)/{ \displaystyle \int }_{ {S}_{{\rm{a}}} }^{}\sigma {\rm{d}}s$ρ：等离子体密度
t：放电时间
$ v $：电弧运动速度
${{\boldsymbol{v}}}_{i}\mathrm{、}{{\boldsymbol{v}}}_{k}$：不同方向上的速度矢量
${x}_{i}\mathrm{，}{x}_{k}$：笛卡尔坐标
$ p： $压力
$ \mathrm{\eta } $：黏度系数
$ J： $电流密度
$ B $：磁感应强度
$ H： $动态热焓
$ \lambda ： $热导率
$ T： $温度
$ {S}_{ {{\rm{R}}}}： $辐射冷却
$ \sigma ： $电导率
$ {E}_{\mathrm{a}\mathrm{r}\mathrm{c}} $：弧柱区电场
强度
$ I： $流过弧柱截面的电流
$ {s}_{\mathrm{a}} $：弧柱截面
$ s： $截面积文献[34-35] 分离瞬间动态热过程，能量守恒方程：${\rho }_{ {\rm{eq} } }{C}_{ {\rm{p} } }\dfrac{\partial T}{\partial t}+{\rho }_{ {\rm{eq} } }{C}_{ {\rm{p} } }{\boldsymbol{u} } \cdot \nabla T+\nabla \cdot \left(-{k}_{ {\rm{eq} } }\nabla T\right)=\dfrac{ {J}^{2} }{\sigma_{\rm{eq} } }$
粒子守恒方程：$\dfrac{\partial {n}_{ {\rm{a} } } }{\partial t}+\nabla \cdot {\varGamma }_{ {\rm{a} } }={R}_{ {\rm{a} } }$
电子能量守恒方程：
$\dfrac{\partial {n}_{{\rm{e}} {\text{ε} } } }{\partial t}+\nabla \cdot {\varGamma }_{{\rm{e}} {\text{ε} } }+E {\varGamma }_{ {\rm{e} } }={R}_{ {\rm{e} }{\rm{ {\text{ε} } } } }$
基于MS方程的重物质输运过程表征：$\mathrm{\rho }\dfrac{\partial }{\partial t}{w}_{k}+\rho \left({\boldsymbol{u} } \cdot \nabla \right){w}_{k}=\nabla \cdot {j}_{k}+{R}_{k}$${\rho }_{{\rm{eq}}}$：等效密度
${C}_{{\rm{p}}}$：等效恒压热容
$ T $：温度
$ t $：时间
$ \boldsymbol{u} $：液态金属速度矢量
$\nabla$：哈密顿算子
${k}_{{\rm{eq}}}$：等效导热系数
$ J $：电流密度
$ {\sigma }_{\rm{eq}} $：等效电导率
na：粒子a的数量
${\varGamma }_{{\rm{a}}}$：粒子a的通量
${R}_{{\rm{a}}}$：粒子a生成或去除
的源项
${n}_{{\rm{e {\text{ε}} }}}$：平均电子能
${\varGamma }_{{\rm{e {\text{ε}} }} }$：电子能通量
E：电场强度
${\varGamma }_{{\rm{e}}}$：电子通量
${R}_{{\rm{e } {\text{ε}} }}$：所有碰撞损耗能量之和
$ \rho $：混合物密度
$ {w}_{k} $：第k个物质质量
分数
$ {j}_{k} $：第k个物质扩散流通量
$ {R}_{k} $：第k个物质速率
下载: 导出CSV
-
[1] ZHAKISHEVA L. 中亚与中国能源合作研究[D]. 上海: 上海外国语大学, 2017.ZHAKISHEVA L. Research on energy cooperation between Central Asia and China[D]. Shanghai: Shanghai International Studies University, 2017. [2] 徐腾飞,王学兵. 近十年我国低瓦斯煤矿瓦斯爆炸事故统计与规律分析[J]. 矿业安全与环保,2021,48(3):126-130.XU Tengfei,WANG Xuebing. Statistics and regularity analysis of gas explosion accidents in domestic low-gas coal mines in recent ten years[J]. Mining Safety & Environmental Protection,2021,48(3):126-130. [3] 景国勋,刘孟霞. 2015—2019年我国煤矿瓦斯事故统计与规律分析[J]. 安全与环境学报,2022,22(3):1680-1686.JING Guoxun,LIU Mengxia. Statistics and analysis of coal mine gas accidents in China from 2015 to 2019[J]. Journal of Safety and Environment,2022,22(3):1680-1686. [4] GB/T 3836.4—2021 爆炸性环境 第4部分: 由本质安全型“i”保护的设备[S].GB/T 3836.4-2021 Explosive atmosheres-part 4: equipment protection by intrinsic safety "i" [S]. [5] 章良海, 宋雅亭, 刘小周. 安全火花原理及应用[M]. 北京: 煤炭工业出版社, 1984.ZHANG Lianghai, SONG Yating, LIU Xiaozhou. Principle and application of safety spark[M]. Beijing: China Coal Industry Publishing House, 1984. [6] 刘鸿浩,李全. 电感性本质安全电路电弧放电的理论分析与实验研究[J]. 煤炭学报,1990,15(2):15-22. doi: 10.3321/j.issn:0253-9993.1990.02.001LIU Honghao,LI Quan. Theoretical and experimental analysis of arc discharge in inductive and intrinsically safe circuits[J]. Journal of China Coal Society,1990,15(2):15-22. doi: 10.3321/j.issn:0253-9993.1990.02.001 [7] 于月森. 本质安全型开关电源基础理论与应用研究[D]. 徐州: 中国矿业大学, 2012.YU Yuesen. Study on the theory and application of the intrinsically safe switch power supply[D]. Xuzhou: China University of Mining and Technology, 2012. [8] 付垚. 电感分断电弧放电机理及建模研究[D]. 西安: 西安科技大学, 2017.FU Yao. Research on mechanism and modeling of inductor disconnected arc discharged[D]. Xi'an: Xi'an University of Science and Technology, 2017. [9] 井莉楠. 本质安全电路电弧放电特性与非爆炸检测方法的研究[D]. 焦作: 河南理工大学, 2007.JING Linan. The research on characteristic of arc discharge of intrinsically safe circuits and non-explosion detecting method[D]. Jiaozuo: Henan Polytechnic University, 2007. [10] 孟庆海,田媛. 本质安全电路模拟储能元件潜在危险性分析及其本质安全判据[J]. 电工技术学报,2022,37(3):676-685. doi: 10.19595/j.cnki.1000-6753.tces.201466MENG Qinghai,TIAN Yuan. Analysis of potential hazards of analog energy storage components in the intrinsic safety circuits and their intrinsic safety criteria[J]. Transactions of China Electrotechnical Society,2022,37(3):676-685. doi: 10.19595/j.cnki.1000-6753.tces.201466 [11] 克拉夫钦克·B·C. 安全火花电路[M]. 张丙军, 译. 北京: 煤炭工业出版社, 1981.КРАВЧЕНКО B С. Safety spark circuit[M]. ZHANG Bingjun, translated. Beijing: China Coal Industry Publishing House, 1981. [12] 孟庆海,许允之,胡天禄. 电感性本质安全电路电弧放电伏安特性分析[J]. 中国矿业大学学报,1999,28(4):79-81.MENG Qinghai,XU Yunzhi,HU Tianlu. Analysis of arc discharge VA characteristics in inductive intrinsically safe circuits[J]. Journal of China University of Mining & Technology,1999,28(4):79-81. [13] 孟庆海,胡天禄. 本质安全电路放电时间及放电能量分布规律[J]. 西安矿业学院学报,1999,19(3):264-267.MENG Qinghai,HU Tianlu. On distribution law of arc discharge current and energy in intrinsically safe circuits[J]. Journal of Xi'an Mining Institute,1999,19(3):264-267. [14] 孟庆海,胡天禄,牟龙华. 本质安全电路低能电弧放电特性及参数[J]. 电工技术学报,2000,15(3):28-30,35. doi: 10.3321/j.issn:1000-6753.2000.03.007MENG Qinghai,HU Tianlu,MU Longhua. Low energy arc discharge characteristic and parameters of intrinsically safe circuits[J]. Transactions of China Electrotechnical Society,2000,15(3):28-30,35. doi: 10.3321/j.issn:1000-6753.2000.03.007 [15] 孟庆海,牟龙华,何学秋. 电感性本质安全电路动态伏安特性参数的确定[J]. 中国矿业大学学报,2001,30(3):51-53.MENG Qinghai,MU Longhua,HE Xueqiu. Determination of dynamic V-A characteristic parameters of inductive intrinsically safe circuits[J]. Journal of China University of Mining & Technology,2001,30(3):51-53. [16] 孟庆海,牟龙华,王崇林,等. 低能电弧放电瞬间的特性分析[J]. 西安科技学院学报,2002,22(1):56-58.MENG Qinghai,MU Longhua,WANG Chonglin,et al. Characteristics of low energy arc discharging instant[J]. Journal of Xi'an University of Science and Technology,2002,22(1):56-58. [17] 孟庆海,王进己. 本质安全电感电路电弧放电时间双正态分布[J]. 电工技术学报,2017,32(2):119-124.MENG Qinghai,WANG Jinji. Dual normal distribution of arc discharge time for inductive intrinsically safe circuits[J]. Transactions of China Electrotechnical Society,2017,32(2):119-124. [18] 赵永秀,王骑,王瑶. 电极分断速度对电感分断放电特性的影响分析与建模[J]. 煤炭学报,2019,44(增刊2):754-762. doi: 10.13225/j.cnki.jccs.2019.0723ZHAO Yongxiu,WANG Qi,WANG Yao. Arc equivalent resistance modeling of inductor-disconnected-discharged arc considering electrode breaking speed[J]. Journal of China Coal Society,2019,44(S2):754-762. doi: 10.13225/j.cnki.jccs.2019.0723 [19] 赵永秀,刘树林,马一博. 爆炸性试验电感电路分断放电特性分析与建模[J]. 煤炭学报,2015,40(7):1698-1704. doi: 10.13225/j.cnki.jccs.2014.1286ZHAO Yongxiu,LIU Shulin,MA Yibo. Analysis and modeling of inductor-disconnected-discharged characteristics based on explosive test[J]. Journal of China Coal Society,2015,40(7):1698-1704. doi: 10.13225/j.cnki.jccs.2014.1286 [20] SHEKHAR R, UBER C. Modeling of sparking contacts for hazardous area applications[C]. IEEE 61st Holm Conference on Electrical Contacts, 2015: 347-352. [21] 刘树林. 本质安全开关变换器基础理论及关键技术研究[D]. 西安: 西安科技大学, 2007.LIU Shulin. Basic theory & key technologies of intrinsically safe switching converters[D]. Xi'an: Xi'an University of Science and Technology, 2007. [22] 刘树林,钟久明,樊文斌,等. 电容电路短路火花放电特性及其建模研究[J]. 煤炭学报,2012,37(12):2123-2128. doi: 10.13225/j.cnki.jccs.2012.12.017LIU Shulin,ZHONG Jiuming,FAN Wenbin,et al. Short circuit discharge characteristics of the capacitive circuit and its mathematical model[J]. Journal of China Coal Society,2012,37(12):2123-2128. doi: 10.13225/j.cnki.jccs.2012.12.017 [23] 刘建华. 爆炸性气体环境下本质安全电路放电理论及非爆炸评价方法的研究[D]. 徐州: 中国矿业大学, 2008.LIU Jianhua. A study on discharge theory and non-explosion evaluating method of the intrinsically safe circuits for explosive atmospheres[D]. Xuzhou: China University of Mining and Technology, 2008. [24] 于月森,张望,孟庆海,等. 截止型保护方式下容性电路短路火花放电模型及分析[J]. 煤炭学报,2013,38(3):517-521. doi: 10.13225/j.cnki.jccs.2013.03.029YU Yuesen,ZHANG Wang,MENG Qinghai,et al. Modeling and analysis on spark discharge of capacitive circuit with cut-off type protection[J]. Journal of China Coal Society,2013,38(3):517-521. doi: 10.13225/j.cnki.jccs.2013.03.029 [25] ZELLER P. A simple arc model for the simulation of the clearing time of drawn arcs with a commercial electronics simulation tool[C]. IEEE 55th Holm Conference on Electrical Contacts, Vancouver, 2009: 67-74. [26] UBER C,SHEKHAR R,FELGNER A,et al. Experimental investigation of low-voltage spark ignition caused by separating electrodes[J]. Journal of Loss Prevention in the Process Industries,2017,49:822-831. doi: 10.1016/j.jlp.2017.03.015 [27] UBER C,HILBERT M,FELGNER A,et al. Electrical discharges caused by opening contacts in an ignitable atmosphere-part I:analysis of electrical parameters at ignition limits[J]. Journal of Loss Prevention in the Process Industries,2019,61:114-121. doi: 10.1016/j.jlp.2019.06.011 [28] UBER C,RUNGE T,BRUNZENDORF J,et al. Electrical discharges caused by opening contacts in an ignitable atmosphere-part II:spectroscopic investigation and estimation of temperatures[J]. Journal of Loss Prevention in the Process Industries,2019,61:213-219. doi: 10.1016/j.jlp.2019.05.010 [29] 郑殿春. 气体放电数值仿真方法[M]. 北京: 科学出版社, 2016.ZHENG Dianchun. Numerical simulation methods for gas discharge[M]. Beijing: Science Press, 2016. [30] 钟久明,刘树林,王玉婷,等. 基于模拟电荷法的微间隙场增强因子研究[J]. 电子学报,2016,44(4):1003-1008. doi: 10.3969/j.issn.0372-2112.2016.04.035ZHONG Jiuming,LIU Shulin,WANG Yuting,et al. Study on the electric field enhancement factor for micro-gap based on CSM[J]. Acta Electronica Sinica,2016,44(4):1003-1008. doi: 10.3969/j.issn.0372-2112.2016.04.035 [31] 王党树,古东明,栾哲哲,等. 基于PIC/MCC法爆炸性气体环境下的微尺度放电特性[J]. 高电压技术,2021,47(3):805-815. doi: 10.13336/j.1003-6520.hve.20201735WANG Dangshu,GU Dongming,LUAN Zhezhe,et al. Micro-scale discharge characteristics in explosive gas environment based on PIC/MCC method[J]. High Voltage Engineering,2021,47(3):805-815. doi: 10.13336/j.1003-6520.hve.20201735 [32] 王党树,栾哲哲,古东明,等. 基于电荷等效法的电容短路放电微观特性数值模拟研究[J]. 电工技术学报,2021,36(13):2684-2696. doi: 10.19595/j.cnki.1000-6753.tces.L90377WANG Dangshu,LUAN Zhezhe,GU Dongming,et al. Numerical simulation research on microscopic characteristics of capacitor short-circuit discharge based on charge equivalent method[J]. Transactions of China Electrotechnical Society,2021,36(13):2684-2696. doi: 10.19595/j.cnki.1000-6753.tces.L90377 [33] 李兴文,陈德桂. 空气开关电弧的磁流体动力学建模及特性仿真[J]. 中国电机工程学报,2007,27(21):31-37. doi: 10.3321/j.issn:0258-8013.2007.21.006LI Xingwen,CHEN Degui. Magnetohydrodynamics modeling and characteristics simulation of air switching arc[J]. Proceedings of the CSEE,2007,27(21):31-37. doi: 10.3321/j.issn:0258-8013.2007.21.006 [34] 付思,曹云东,李静,等. 真空开关电器中接触触点热过程的仿真研究[J]. 真空科学与技术学报,2019,39(7):546-551. doi: 10.13922/j.cnki.cjovst.2019.07.03FU Si,CAO Yundong,LI Jing,et al. Heat transfer of electrical contact in vacuum interrupter:a simulation study[J]. Chinese Journal of Vacuum Science and Technology,2019,39(7):546-551. doi: 10.13922/j.cnki.cjovst.2019.07.03 [35] 付思,曹云东,李静,等. 触头分离瞬间真空金属蒸气电弧形成过程的仿真[J]. 电工技术学报,2020,35(13):2922-2931. doi: 10.19595/j.cnki.1000-6753.tces.190708FU Si,CAO Yundong,LI Jing,et al. Simulation researches on vacuum metal vapor arc formation at the initial moment of contact parting[J]. Transactions of China Electrotechnical Society,2020,35(13):2922-2931. doi: 10.19595/j.cnki.1000-6753.tces.190708 [36] 赵永秀,刘树林,王瑶,等. 安全火花试验电极热场致发射模型和温度效应的数值模拟研究[J]. 电工技术学报,2019,34(20):4179-4187. doi: 10.19595/j.cnki.1000-6753.tces.L80745ZHAO Yongxiu,LIU Shulin,WANG Yao,et al. Research on numerical simulation of thermal field electron emission and temperature effect for safety spark test electrode[J]. Transactions of China Electrotechnical Society,2019,34(20):4179-4187. doi: 10.19595/j.cnki.1000-6753.tces.L80745 -
点击查看大图
图(12) / 表(3)
计量
- 文章访问数: 209
- HTML全文浏览量: 59
- PDF下载量: 31
- 被引次数: 0
