0 引言
作为煤矿安全生产重要巡检设备的矿用智能巡检机器人因具有较强的环境适应力、自主巡检力等优势在煤矿生产以及其他极端环境下得到了广泛应用[1]。利用矿用智能巡检机器人可以减轻现场人员的工作压力,节省人力成本,提高巡检效率。矿用智能巡检机器人在巡检时需要获取外部环境信息,由此来驱动其完成相关巡检任务,而煤矿环境具有作业空间狭小、视觉环境差、温度高的特点,因此,对矿用智能巡检机器人如何更加准确获取视觉信息,并高效执行相应巡检任务提出了更高要求。视觉伺服控制技术是一种能够精准获取机器人工作环境信息,并通过一定的映射关系将视觉信息转换到机械臂关节角的运动空间中,通过速度控制器驱动机器人运动的关键技术。良好的视觉伺服控制策略不仅可以保证智能巡检机器人作业精度,还能使其在复杂环境下稳定运行以完成巡检任务。视觉伺服控制对于矿用智能巡检机器人的控制具有重要作用。
传统的基于图像的视觉伺服(Image-Based Visual Servoing,IBVS)控制和基于位置的视觉伺服控制都需要依靠模型标定技术,这些模型主要涉及机器人模型和摄像机模型,视觉伺服系统的整体性能受模型标定的影响,要实现高精度的模型标定比较困难。因为不论是对相机内外参数的标定还是对机器人运动学模型的标定都存在一定缺陷,比如系统结构的变化、摄像机位置与焦距的变化以及高温强辐射等都会使标定结果产生很大误差,且标定成本较高,所以无标定视觉伺服技术备受瞩目。
无标定视觉伺服是在没有对相机模型和机器人模型进行标定的情况下,利用摄像机获得的视觉信息形成闭环系统来驱动机器人运动,完成相关的视觉伺服任务。无标定视觉伺服技术的核心问题是计算末端执行器的图像特征变化率与空间速度之间的映射关系,这通常反映在图像雅可比矩阵中。IBVS控制器利用图像雅可比矩阵的逆或伪逆映射图像特征误差,生成控制信号。康庆生等[2]提出了一种递推最小二乘法估计图像雅可比矩阵的伪逆矩阵,无需计算雅可比矩阵伪逆,计算较简单。赵杰等[3]利用动态拟牛顿法估计图像雅克比矩阵, 采用迭代最小二乘法提高系统的稳定性。以上2种方法在雅可比矩阵估计中存在容易受环境噪声干扰的风险,为此,赵清杰等[4]针对非线性高斯系统提出了利用粒子滤波算法估计雅可比矩阵,并通过实验验证了该方法不仅能避免系统标定,而且对系统噪声的类型没有具体要求。徐鹏等[5]在非高斯环境下采用一种扩展H∞粒子滤波算法对图像雅可比矩阵进行在线辨识,提高了机器人轨迹跟踪精度,但该算法存在收敛性不高的缺陷。Wang Fasheng等[6]提出了无迹粒子滤波器在线估计雅可比矩阵值方法,该方法在目标跟踪任务中具有准确可靠的性能,但对于多自由度的机器人性能不佳。梁喜凤等[7]提出了一种基于自适应无迹卡尔曼滤波器的拾取机械手伺服控制方法,该方法对扰动噪声适应性较强,但实时性不高。王新梅等[8]结合卡尔曼滤波中噪声的数学特性, 构建了鲁棒卡尔曼滤波模型,实现了时延情况下图像雅可比矩阵较为准确的估计。王洪斌等[9]针对卡尔曼滤波中状态向量的速度分量进行再估计,提出了一种修正卡尔曼滤波器对目标物体远程运动估计的算法,提高了估计精度,但存在稳定性能差的缺点。近年来神经网络因具有高速并行分布式处理的特点被广泛应用,章晓峰等[10]利用BP神经网络确定了机器人基座坐标系和摄像机坐标系之间的非线性映射关系,通过分拣机器人系统实验证明了该神经网络能够提高手眼标定的精确度。Z.R.Tsai等[11]提出了一种带有抽头延迟的递归神经网络(RNN), 解决了视觉伺服系统的时变时滞控制问题,该算法收敛性较高,但同时存在稳定性不高的问题。Chi Gaoxuan[12] 和Gu Jinan 等[13]结合计算机视觉技术和模糊理论,提出了一种基于模糊神经网络的视觉伺服控制策略,利用模糊神经网络逼近目标图像特征与机器人关节位置变化之间的映射关系,不仅降低了计算量,且提高了雅可比矩阵估计精度。F.Nadi等[14]利用人工神经网络对图像雅可比矩阵的伪逆进行估计,建立了目标特征点视觉空间速度信息与机器人关节空间的映射关系,使伺服控制器能够跟踪运动目标,但该方法不能提高视觉伺服控制系统的稳定性。M.Mitic等[15]提出了一种基于人工神经网络的智能机器人移动学习方法,分别在离线和在线阶段建立了图像空间与执行器之间的映射关系。但上述方法求得的雅可比矩阵都不是最优解,机械手在笛卡尔空间中的路径也不是最优和近似最优的,在无标定视觉伺服控制精度与鲁棒性上不能同时表现出良好的性能。
针对现有矿用智能巡检机器人无标定视觉伺服控制中图像雅可比矩阵估计值不准确、鲁棒性差的问题,提出了一种具有长短期记忆(Long and Short Term Memory, LSTM)的卡尔曼滤波(Kalman Filtering,KF)算法(KFLSTM算法),该算法使用LSTM弥补由KF算法产生的估计误差,将滤波增益误差、状态估计向量误差、观测误差用于LSTM的在线训练,利用训练后的LSTM模型对雅可比矩阵进行最优估计,成功解决了KF算法对雅可比矩阵估计值不准确的问题。基于KFLSTM算法建立了无标定视觉伺服控制模型,并将KFLSTM算法应用在六自由度机器人视觉伺服仿真实验中。仿真结果表明,基于该算法的IBVS控制模型对噪声具有鲁棒性,视觉伺服控制精度高。
1 基于KF的图像雅可比矩阵在线估计
1.1 图像雅可比矩阵模型
基于图像的无标定视觉伺服控制需要建立图像特征空间与机械臂运动空间之间的映射关系,并尽量减少当前图像特征与所需图像特征之间的误差。而基于图像雅可比矩阵的方法是目前在无标定视觉伺服中常用的一类方法,该方法的主要特点就是使用图像雅可比矩阵模型来描述机器人手眼映射关系。
定义图像特征误差为
e=S-S*
(1)
式中:e为当前图像特征值与所需图像特征值之间的误差;S为当前图像的特征值;S*为所需图像的特征值。
图像特征在IBVS系统中的变化率与关节角的变化率之间的映射关系为
(2)
式中:![]() 为图像特征的变化率;Jq为图像雅可比矩阵,Jq随机械臂位置的变化而变化,它的值在当前关节角的范围内是有效的;
为图像特征的变化率;Jq为图像雅可比矩阵,Jq随机械臂位置的变化而变化,它的值在当前关节角的范围内是有效的;![]() 为关节角的变化率。
为关节角的变化率。
机械臂关节角变化率与图像雅可比矩阵之间的关系为
(3)
式中:λ为控制算法的增益;![]() 为Jq的伪逆矩阵。
为Jq的伪逆矩阵。
为了解决经典IBVS控制系统中的雅可比矩阵Jq及其伪逆矩阵![]() 无法获得精确值的问题,实现无标定的手眼协调,采用了一种基于KF算法的图像雅可比矩阵估计模型。
无法获得精确值的问题,实现无标定的手眼协调,采用了一种基于KF算法的图像雅可比矩阵估计模型。

(4)
式中:qi(i=1,2,…,n)为机器人第i个关节角度,n为关节角个数;sj(j=1,2,…,m)为第j个图像特征,m为图像特征个数。
该矩阵反映了机器人末端执行器运动空间到图像特征空间的变换关系。因此,对雅可比矩阵的估计问题便成了无标定视觉伺服控制的关键问题,本文引入KF算法将图像雅可比矩阵估计问题转换为对系统的状态观测问题。
视觉空间-运动空间满足非线性映射关系:
(5)
式中ve(t)为t时刻机器人末端执行器速度。
1.2 KF算法分析
传统的KF算法是一种独立高斯白噪声下的最优线性状态估计算法,可用于雅可比矩阵的在线估计,KF的状态模型和观测模型分别为
X(t)=Φ(t,t-1)X(t-1)+W(t)
(6)
Z(t)=H(t)X(t)+V(t)
(7)
式中:X(t)为系统的状态向量,主要由雅可比矩阵的行向量组成;Φ(t,t-1)为状态转移矩阵,一般情况下取单位矩阵;W(t)为状态噪声矩阵;Z(t)为系统的观测向量;H(t)为系统的观测矩阵;V(t)为观测噪声矩阵,W(t)和V(t)都是均值为零、协方差分别为Q(t)和R(t)的白噪声矩阵。
在无标定视觉伺服系统中,将系统的观测向量Z(t)和观测矩阵H(t)分别表示为
(8)

(9)
基于KF的状态估计可分为2步进行:第1步为状态向量和误差协方差矩阵的预测过程;第2步为滤波增益、状态向量和误差协方差矩阵的更新过程。
预测过程公式为
(10)
P(t/t-1)=Φ(t,t-1)P(t-1)Φ(t,t-1)T+
Φ(t,t-1)Q(t-1)Φ(t,t-1)T
(11)
更新过程公式为
K(t)=P(t/t-1)H(t)T(H(t)P(t/t-1)×
H(t)T+R(t))-1
(12)
(13)
P(t)=(1-K(t)H(t))P(t/t-1)×
(1-K(t)H(t))T+K(t)R(t)K(t)T
(14)
式中:![]() 和
和![]() 分别为t时刻和t-1时刻的状态预测向量;P(t/t-1)为t时刻预测误差协方差矩阵;P(t)为t时刻滤波误差协方差矩阵;Q(t-1)为系统过程噪声协方差矩阵;K(t)为滤波增益矩阵;R(t)为系统观测噪声协方差矩阵。
分别为t时刻和t-1时刻的状态预测向量;P(t/t-1)为t时刻预测误差协方差矩阵;P(t)为t时刻滤波误差协方差矩阵;Q(t-1)为系统过程噪声协方差矩阵;K(t)为滤波增益矩阵;R(t)为系统观测噪声协方差矩阵。
由上述KF算法分析可知,KF是一种对高斯白噪声下的线性系统的状态变量进行最优估计的有效方法。
2 改进KF算法
KF是在环境噪声为高斯白噪声下的最优线性状态估计,但是在机器人运动的真实环境中由机器人末端执行器引入的噪声并不是简单的高斯白噪声,这就导致了KF的估计变成了次优估计。为了得到最优估计,本文提出了 LSTM网络误差补偿模型,实现了非线性滤波动态补偿。
(15)
式中:![]() 为KF的次优估计;
为KF的次优估计;![]() 为经过误差补偿后的最优估计;
为经过误差补偿后的最优估计;![]() 为KF估计误差。
为KF估计误差。
2.1 LSTM构建
LSTM是一种改良的递归神经网络,它与传统的递归神经网络相比能够很好地降低梯度消失和梯度爆炸的风险,并且能够更好地处理长期依赖问题。LSTM的主要结构是3个门单元,它们分别是输入门、遗忘门和输出门。输入门表示要保存的信息或者待更新的信息,遗忘门决定丢弃哪些信息,输出门决定当前神经元细胞输出的隐向量。在本文中,LSTM起到了精确的误差估计器的作用,其任务是将期望状态与估计状态之间的误差最小化。LSTM结构如图1所示。

图1 LSTM结构
Fig.1 LSTM structure
LSTM在实现信息传递的过程中首先是将当前单元的状态输入和前一个单元的隐藏层向量经过遗忘门输出一个遗忘向量,遗忘门将删除不相关的信息。该过程的实现方程为
(16)
式中:![]() 为遗忘门的输出结果;σ为sigmoid函数,是logistic回归使用的激活函数,sigmoid层决定哪些信息需要更新,输出值域为(0,1),0表示全抛弃,1表示全保留;ωf为遗忘门的权重矩阵;h〈t-1〉,x〈t〉分别为前一个单元的隐藏层向量和当前单元的状态输入;bf为遗忘门的偏置。
为遗忘门的输出结果;σ为sigmoid函数,是logistic回归使用的激活函数,sigmoid层决定哪些信息需要更新,输出值域为(0,1),0表示全抛弃,1表示全保留;ωf为遗忘门的权重矩阵;h〈t-1〉,x〈t〉分别为前一个单元的隐藏层向量和当前单元的状态输入;bf为遗忘门的偏置。
当前单元的状态输入和前一个单元的隐藏层向量会通过tanh函数计算当前单元的候选状态,这一层将保存可能会加入细胞状态的信息,并通过一个输入门来决定有哪些信息要更新到网络的长期记忆中。该过程的实现方程为
(17)
(18)
(19)
式中:![]() 为输入门的输出结果;ωg为输入门的权重矩阵;bg为输入门的偏置;
为输入门的输出结果;ωg为输入门的权重矩阵;bg为输入门的偏置;![]() 为当前时刻输入经过激活单元的输出结果;tanh激活函数为
为当前时刻输入经过激活单元的输出结果;tanh激活函数为![]() 一个tanh层生成一个向量,输出为(-1,1),也就是备选的用来更新的内容;ωl为激活单元权重矩阵;bl为激活单元的偏置;c〈t〉为当前控制单元状态的输出结果。
一个tanh层生成一个向量,输出为(-1,1),也就是备选的用来更新的内容;ωl为激活单元权重矩阵;bl为激活单元的偏置;c〈t〉为当前控制单元状态的输出结果。
当前单元细胞的长期记忆会通过一个输出门结构得到当前输出信息和当前隐藏层信息。该过程的实现方程为
(20)
(21)
式中:![]() 为输出门的输出结果;ω0为输出门的权重矩阵;b0为输出门的偏置。
为输出门的输出结果;ω0为输出门的权重矩阵;b0为输出门的偏置。
2.2 神经网络误差补偿模型
基于LSTM的误差补偿模型如图2所示,将经由KF得到的增益误差![]() 状态估计误差
状态估计误差![]() 和观测误差
和观测误差![]() 作为补偿神经网络的训练输入,利用KF在每个过程中得到的雅可比矩阵与期望的雅可比矩阵之差作为网络的训练输出。LSTM 网络训练时,控制单元的最优参数由梯度下降的方法得到。经过LSTM补偿后的模型能将KF的次优估计转化为最优估计,以提高雅可比矩阵估计的精确度。
作为补偿神经网络的训练输入,利用KF在每个过程中得到的雅可比矩阵与期望的雅可比矩阵之差作为网络的训练输出。LSTM 网络训练时,控制单元的最优参数由梯度下降的方法得到。经过LSTM补偿后的模型能将KF的次优估计转化为最优估计,以提高雅可比矩阵估计的精确度。

图2 基于LSTM的误差补偿模型
Fig.2 Error compensation model based on LSTM
改进KF图像雅可比矩阵在线估计算法步骤如下:
步骤1:输入上一个时刻即t-1时刻图像雅可比矩阵![]() 协方差矩阵P(t-1)和卡尔曼增益K(t-1)。
协方差矩阵P(t-1)和卡尔曼增益K(t-1)。
步骤2:获取当前图像特征的观测值Z(t)。
步骤3:根据式(10)、式(11),由预测步骤估计下一时刻的状态值和协方差矩阵。
步骤4:根据式(12)—式(14),由更新步骤计算KF增益K(t),状态更新值![]() 和协方差矩阵P(t)。
和协方差矩阵P(t)。
步骤5:输出![]()
步骤6:计算增益误差![]() 滤波状态估计误差
滤波状态估计误差![]() 观测误差
观测误差![]()
步骤7:根据图2训练的LSTM进行误差估计补偿![]()
步骤8:计算图像雅可比矩阵的最优估计值![]()
3 基于改进KF算法的无标定视觉伺服模型
为了在无标定视觉伺服控制中获得更准确的雅可比矩阵估计值,采用了基于LSTM补偿的KF算法(KFLSTM算法),通过该算法获得雅可比矩阵最优值,进而得到雅可比矩阵广义逆与特征误差矩阵的乘积,使控制器输出准确的关节角速度,从而控制机械臂的实时运行,提高视觉伺服控制的精度和收敛速度。基于KFLSTM算法的无标定视觉伺服控制模型框架如图3所示。首先用传统的KF算法估计图像雅可比矩阵,得到KF的滤波增益误差、状态估计误差和观测误差,将3个误差向量构造为单个向量,作为LSTM网络的输入,利用KF在每个过程中得到的雅可比矩阵和期望矩阵的差作为网络的输出,得到一组训练样本,这些训练样本用于训练LSTM神经网络,以确定网络参数。

图3 基于KFLSTM算法的无标定视觉伺服控制模型框架
Fig.3 Framework of uncalibrated visual servo control model based on KFLSTM algorithm
基于KFLSTM算法的无标定视觉伺服控制模型工作流程如下:
Step1:初始化雅可比矩阵,在开始阶段给定机器人任意k步线性无关的试探运动dq1,dq2,…,dqk,得到图像特征变化ds1,ds2,…,dsk,从而获得状态初始值![]() 即
即![]()
[ds1,ds2,…,dsk][dq1,dq2,…,dqk]-1
(22)
Step2:根据当前机械臂运动速度![]() 由式(9)得到观测矩阵H(t-1)。
由式(9)得到观测矩阵H(t-1)。
Step3:根据KF的观测步骤和更新步骤,由t-1时刻的最优图像雅可比矩阵![]() 得到t时刻的次优图像雅可比矩阵
得到t时刻的次优图像雅可比矩阵![]()
Step4:用已经训练好的LSTM对卡尔曼估计误差![]() 进行误差补偿,从而得到t时刻的最优值
进行误差补偿,从而得到t时刻的最优值![]()
Step5:由控制规则获得机械臂关节速度, 控制机器人从当前位姿运动到下一时刻位姿,利用摄像机获取图像特征,若此时图像特征误差在收敛阈值范围内,则结束IBVS循环,否则继续用KFLSTM模型进行下一时刻(t+1)的图像雅可比矩阵估计。
4 实验结果与分析
4.1 实验条件与参数设置
本文对基于KFLSTM算法的无标定视觉伺服控制模型的可行性进行了仿真实验,并与经典的基于KF算法和已经取得较好性能的KFRBF(基于径向基函数的卡尔曼滤波)算法进行比较。仿真实验在Matlab环境下进行。仿真均以PUMA560机械臂为仿真模型,同时利用机器视觉工具箱搭建了摄像机模型,其中摄像机模型参数设置如下:焦距为8 mm,相位平面为1 024×1 024,主点坐标为(512,512),采样频率为20 Hz。
在仿真实验中,选取某一物体上的4个点即A,B,C,D的空间坐标作为无标定视觉伺服控制模型的目标特征点,且特征点在笛卡尔坐标系中的坐标为P,初始图像特征为S0,期望图像特征为S*,机械臂的初始角度为q0。图像特征误差收敛阈值为ethr=0.5。
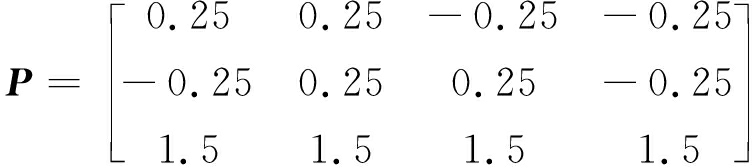
(23)
设置初始图像特征点像素位置为
S0=[xA,yA,xB,yB,xC,yC,xD,yD]T=
[286.93,182.33,370.59,184.52,368.22,
284.01,285.18,275.86]T
(24)
期望图像特征点像素位置为
S*=![]()
[453.82,78.35,445.59,423.12,148.17,
420.77,156.06,70.69]T
(25)
机械臂的初始角度为
(26)
4.2 实验结果分析
在仿真实验中,在训练前不添加LSTM的情况下,由KF过程得到滤波增益误差![]() 状态估计误差
状态估计误差![]() 观测误差
观测误差![]() 作为神经网络的输入训练样本,输出样本来自期望状态与KF估计状态之间的误差。采用梯度下降法来获得各控制单元最优参数,以此让LSTM来进一步纠正和补偿误差。
作为神经网络的输入训练样本,输出样本来自期望状态与KF估计状态之间的误差。采用梯度下降法来获得各控制单元最优参数,以此让LSTM来进一步纠正和补偿误差。
在机器人仿真实验中,设λ=0.5,并在实验过程中按照经验加入均值为0、方差为0.2的随机扰动噪声。同时为了进一步说明提出算法的优越性,与现已取得较好性能的KFRBF算法及经典KF算法做了对比实验。本文采用收敛速度(图像特征误差达到收敛阈值时的迭代次数)和图像特征累积误差2个性能指标来评价机械手视觉伺服控制模型的性能。
(27)
(28)
式中:dc为图像特征误差达到最小值时的迭代次数;d为迭代次数,1≤d≤dc;e(d)为第d次迭代的图像特征误差;eLAE为图像特征累积误差。
4.2.1 与其他方法的对比实验
在扰动方差为0.2时基于KFLSTM、KFRBF以及KF算法的仿真结果如图4—图6所示。其中图4(a)、图5(a)、图6(a)为A,B,C,D四个特征点的图像特征轨迹,它表示了随着机器人的移动图像特征在像素坐标系中的轨迹。由于特征点的深度信息在视觉伺服过程中很难实时获取,所以雅可比矩阵计算中存在一定误差。从图4(a)、图5(a)、图6(a)可看出,3种算法中KFLSTM算法得到的图像特征轨迹更接近直线,说明利用KFLSTM算法估计雅可比矩阵精度较高。图4(b)、图5(b)、图6(b)为机器人末端执行器位姿轨迹误差,其中x*-x、y*-y、z*-z是机器人末端执行器分别在3个坐标轴上的位置误差,![]() 分别为末端执行器的姿态误差,该位姿误差表示了机器人6个关节运动过程产生的冗余运动,位姿误差越小说明运动越平稳。从图4(b)、图5(b)、图6(b)可看出,采用KFLSTM算法的末端执行器位姿轨迹误差相对于其他2种算法较小,说明机械手末端执行器在伺服控制中的冗余运动减少,运动较平稳。图4(c)、图5(c)、图6(c)为图像特征误差,
分别为末端执行器的姿态误差,该位姿误差表示了机器人6个关节运动过程产生的冗余运动,位姿误差越小说明运动越平稳。从图4(b)、图5(b)、图6(b)可看出,采用KFLSTM算法的末端执行器位姿轨迹误差相对于其他2种算法较小,说明机械手末端执行器在伺服控制中的冗余运动减少,运动较平稳。图4(c)、图5(c)、图6(c)为图像特征误差,![]() 分别表示A,B,C,D四个特征点在横轴x上的图像特征误差,
分别表示A,B,C,D四个特征点在横轴x上的图像特征误差,![]() 分别表示A,B,C,D四个特征点在纵轴y上的特征误差。图像特征误差的大小反映了控制模型控制误差振荡的能力。从收敛速度和累积误差2种性能来看,基于KFLSTM、KFRBF、KF算法的迭代次数分别为100、148、202,累积误差分别为8.53×103、1.08×104、1.09×104像素, 较少的迭代次数说明了在3种对比算法中,KFLSTM算法的收敛速度最快,累积误差较小,说明KFLSTM算法控制误差振荡的能力最强。
分别表示A,B,C,D四个特征点在纵轴y上的特征误差。图像特征误差的大小反映了控制模型控制误差振荡的能力。从收敛速度和累积误差2种性能来看,基于KFLSTM、KFRBF、KF算法的迭代次数分别为100、148、202,累积误差分别为8.53×103、1.08×104、1.09×104像素, 较少的迭代次数说明了在3种对比算法中,KFLSTM算法的收敛速度最快,累积误差较小,说明KFLSTM算法控制误差振荡的能力最强。

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图4 扰动方差为0.2时基于KFLSTM算法的IBVS仿真结果
Fig.4 IBVS simulation results based on KFLSTM algorithm with disturbance variance of 0.2

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图5 扰动方差为0.2时基于KFRBF算法的IBVS仿真结果
Fig.5 IBVS simulation results based on KFRBF algorithm with disturbance variance of 0.2

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图6 扰动方差为0.2时基于KF算法的IBVS仿真结果
Fig.6 IBVS simulation results based on KF algorithm with disturbance variance of 0.2
4.2.2 鲁棒性实验
为了验证本文算法对不同噪声干扰的鲁棒性,又进行了第2组实验,在实验中,加入方差分别为0.3和0.4的随机扰动,3种算法的实验仿真结果如图7—图12所示, 3种算法的收敛速度和累积误差仿真结果见表1。
将2种方差下的结果与第1组实验一起对比可以得出IBVS在同一算法、不同扰动误差下的性能。从图4(a)—图12(a)可看出,当噪声方差分别为0.2,0.3,0.4时,3种算法图像特征轨迹都无明显变化,图像空间特征全都稳定在相机视场范围内。从图4(b)、图7(b)、图10(b)可以看出,当系统扰动误差由0.2增加到0.3,又由0.3增加到0.4时,末端执行器位姿轨迹误差无明显变化。从图5(b)、图8(b)、图11(b)以及图6(b)、图9(b)、图12(b)可看出,基于KFRBF算法和基于KF算法的IBVS控制模型在扰动误差发生改变时,其末端执行器位姿轨迹误差发生了较大变化,而基于KFLSTM算法的IBVS控制模型具有末端执行器最平滑的运动轨迹,其运动最平稳。另外,从表1可看出,当扰动误差为0.2时KFLSTM、KFRBF、KF算法的迭代次数分别为100、148、202,相对于KF算法,KFLSTM算法收敛速度提高了102%,相较于KFRBF算法提高了48%。同理,扰动误差为0.3时可计算出KFLSTM算法在收敛速度上相较于KF算法提高了122%,相较于KFRBF提高了66%。扰动误差为0.4时,KFLSTM算法的收敛速度比KF算法、KFRBF算法分别提高了142%和75%。从定量的结果分析可以看出,同一扰动误差下,3种对比算法中KFLSTM算法收敛速度最快,且累积误差最小。另外,表1中的性能指标结果显示,KFLSTM算法在不同噪声方差下的迭代次数分别为100、98和102,累积误差分别为8.53×103、8.53×103、8.54×103像素,无明显的误差变化,而另外2种算法只在累积误差方面具有稳定性,因此,与其他算法相比,基于KFLSTM算法的IBVS对噪声具有更强的鲁棒性。
表1 KFLSTM,KFRBF,KF算法仿真结果
Table 1 Simulation results of KFLSTM,KFRBF and KF algorithm

算法迭代次数累积误差/像素0.20.30.40.20.30.4KF2022182471.09×1041.08×1041.11×104KFRBF1481631791.08×1041.09×1041.10×104KFLSTM100981028.53×1038.53×1038.54×103

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图7 扰动方差为0.3时基于KFLSTM算法的IBVS 仿真结果
Fig.7 IBVS simulation results based on KFLSTM algorithm with disturbance variance of 0.3

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图8 扰动方差为0.3时基于KFRBF算法的IBVS 仿真结果
Fig.8 IBVS simulation results based on KFRBF algorithm with disturbance variance of 0.3

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图9 扰动方差为0.3时基于KF算法的IBVS仿真结果
Fig.9 IBVS simulation results based on KF algorithm with disturbance variance of 0.3

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图10 扰动方差为0.4时基于KFLSTM算法的IBVS仿真结果
Fig.10 IBVS simulation results based on KFLSTM algorithm with disturbance variance of 0.4

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图11 扰动方差为0.4时基于KFRBF算法的IBVS仿真结果
Fig.11 IBVS simulation results based on KFRBF algorithm with disturbance variance of 0.4

(a)图像特征轨迹

(b)末端执行器位姿轨迹误差

(c)图像特征误差
图12 扰动方差为0.4时基于KF算法的IBVS仿真结果
Fig.12 IBVS simulation results based on KF algorithm with disturbance variance of 0.4
实验结果表明,基于KFLSTM算法的无标定视觉伺服控制模型中图像误差收敛均在0.5像素内,说明模型定位精度较高,且对噪声具有较强的鲁棒性,在收敛速度、机械手末端执行器的空间运动轨迹和特征误差等方面均表现出了较好的性能。
5 结语
针对矿用智能巡检机器人视觉伺服控制中采用传统的KF算法图像雅可比矩阵存在估计值不准确、鲁棒性差的问题,提出了一种基于KFLSTM算法的无标定视觉伺服控制模型,利用LSTM对KF算法得到的次优状态进行误差补偿,进而获得雅可比矩阵最优估计值。KFLSTM算法通过提高雅可比矩阵估计值的准确性和稳定性来改善视觉伺服控制的实时性和鲁棒性。将KFLSTM算法应用于六自由度机器人视觉伺服控制中,仿真结果表明,利用KFLSTM算法得到的图像特征与传统的KF算法以及KFRBF算法相比,误差更小,误差收敛速度相较于传统KF算法提高了100%~142%,且机器人末端执行器运动平稳,具有较强的抗噪声干扰能力。KFLSTM算法可有效提高巡检机器人的作业精度与效率,并增强其工作的稳定性与安全性。
[1] 潘祥生,陈晓晶.矿用智能巡检机器人关键技术研究[J].工矿自动化,2020,46(10):43-48.
PAN Xiangsheng,CHEN Xiaojing.Research on key technologies of mine-used intelligent inspection robot[J].Industry and Mine Automation,2020,46(10):43-48.
[2] 康庆生,孟正大,戴先中.图像雅可比矩阵伪逆估计在视觉伺服中的应用[J].机器人,2006,28(4):406-409.
KANG Qingsheng,MENG Zhengda,DAI Xianzhong.Application of pseudo-inverse estimation of image Jacobian matrixto visual servoing[J].Robot,2006,28(4):406-409.
[3] 赵杰,李牧,李戈,等.一种无标定视觉伺服控制技术的研究[J].控制与决策,2006,21(9):1015-1019.
ZHAO Jie,LI Mu,LI Ge,et al.Study on uncalibrated visual servoing technique[J].Control and Decision,2006,21(9):1015-1019.
[4] 赵清杰,陈云蛟,张立群.基于粒子滤波的雅可比矩阵在线估计技术[J].北京理工大学学报,2008,28(5):401-404.
ZHAO Qingjie,CHEN Yunjiao,ZHANG Liqun.On-line estimation of Jacobian matrix based on particle filter[J].Transactions of Beijing Institute of Technology,2008,28(5):401-404.
[5] 徐鹏,杨宏韬,李岩,等.基于扩展H∞粒子滤波算法的视觉伺服雅可比矩阵在线辨识[J].广西大学学报(自然科学版),2017,42(3):1051-1057.
XU Peng,YANG Hongtao,LI Yan,et al.On-line identification of visual servo Jacobian matrix based on extended H∞ particle filter[J].Journal of Guangxi University(Natural Science Edition),2017,42(3):1051-1057.
[6] WANG Fasheng,SUN Fuming,ZHANG Junxing,et al.Unscented particle filter for online total image Jacobian matrix estimation in robot visual servoing[J].IEEE Access,2019(99).DOI:10.1109/ACCESS.2019.2927413.
[7] 梁喜凤,彭明,路杰,等.基于自适应无迹卡尔曼滤波的采摘机械手视觉伺服控制方法[J].农业工程学报,2019,35(19):230-237.
LIANG Xifeng,PENG Ming,LU Jie,et al.Servo control method of picking manipulator based on adaptive traceless Kalman filter[J].Transactions of the Chinese Society of Agricultural Engineering,2019,35(19):230-237.
[8] 王新梅,魏武,刘玮,等.鲁棒卡尔曼滤波下的图像雅可比矩阵带时延补偿的估计[J].控制理论与应用,2015,32(8):1052-1057.
WANG Xinmei,WEI Wu,LIU Wei,et al.Estimation of image Jacobian matrix with time-delay compensation basedon robust Kalman filtering[J].Control Theory & Applications,2015,32(8):1052-1057.
[9] 王洪斌,李萍.基于改进的卡尔曼滤波图像雅可比矩阵估计[J].武汉理工大学学报,2009,31(14):145-148.
WANG Hongbin,LI Ping.On-line estimation for image Jacobian matrix based on improved Kalman filter[J].Journal of Wuhan University of Technology,2009,31(14):145-148.
[10] 章晓峰,李光,肖帆,等.基于BP神经网络的包装分拣机器人视觉标定算法[J].包装学报,2019,11(4):74-81.
ZHANG Xiaofeng,LI Guang,XIAO Fan,et al.A visual calibration algorithm for packaging sorting robot based on BP neural network[J].Journal of Packaging Science and Technology,2019,11(4):74-81.
[11] TSAI Z R,CHANG Y Z.Enhancing design of visual-servo delayed system[J].Journal of Electronic Science and Technology of China,2018,16(3):232-240.
[12] CHI Gaoxuan.Application study of fuzzy ARTMAP neural network in robot servo system[J].Journal of Physics Conference Series,2018,1026(1):012024.DOI:10.1088/1742-6596/1026/1/012024.
[13] GU Jinan,WANG Hongmei,PAN Yuelong,et al.Neural network based visual servo control for CNC load/unload manipulator[J].Optik International Journal for Light and Electron Optics,2015,126(23):4489-4492.
[14] NADI F,DERHAMI V,REZAEIAN M.Visual servoing control of robot manipulator with Jacobian matrix estimation[C]//Proceedings of the 2014 International Conference on Robotics and Mechatronics,2014:405-409.DOI:10.1109/ICRoM.2014.6990935.
![]() Z.Neural network learning from demonstration and epipolar geometry for visual control of a nonholonomic mobile robot[J].Soft Computing,2014,18(5):1011-1025.
Z.Neural network learning from demonstration and epipolar geometry for visual control of a nonholonomic mobile robot[J].Soft Computing,2014,18(5):1011-1025.
