0 引言
安全高效的盾构施工法在矿藏开采和隧道开挖中得到了广泛应用。滚刀作为盾构破岩的主要工具,在高温、节理、岩溶和地应力等复杂地质条件下持续工作,其易损耗、成本高、更换复杂等特点使之成为影响工期和造价的重要因素。因此,滚刀生命周期的准确预测对及时掌握盾构机工作状态、提高掘进效率和降低施工成本具有重要意义[1-2]。
近半个世纪以来,国内外众多学者不断开展了对滚刀磨损寿命预测模型的研究,先后从力学角度得出了理论模型、半理论模型、实验模型和工程经验模型[3]。在掌握破岩机理的基础上,G. Wijk[4]于1992年提出了滚刀磨损量与CAI(Cerchar Abrasivity Index)值有关的半理论半经验公式。J. Rostami[5]于1997年提出了美国科罗拉多矿业学院(Colorado School of Mines,CSM)滚刀磨损寿命预测模型。A. Bruland[6]于1998年提出滚刀磨损量与可钻性指数DRI、磨蚀值AV有关,并提出经验法和图表法相结合的挪威科技大学(Norwegian University of Science and Technology,NTNU)滚刀磨损寿命预测模型。上述文献对滚刀磨损寿命预测模型的发展做出了重要贡献,但目前的磨损寿命预测模型的工程实际应用效果并不能令人满意。龚秋明等[7]分别采用CSM模型和NTNU模型对锦屏二级水电站引水涵洞工程的单把滚刀使用寿命和掘进距离进行了预测,结果表明2个模型的计算结果与真实值相差较大,原因是目前模型普遍是针对均匀地质,无法应用于岩石特性不均匀的复杂地层,又因岩体参数、机械参数、掘进参数[8]等诸多影响因素与滚刀磨损寿命预测之间无明确的数学关系且具有时变性,使固定不变的数学函数表达式难以适应多变的工况[9]。进入21世纪后,除了以去除机制为理论基础的磨料磨损模型[2]和以CSM和NTNU模型等为理论基础发展而来的其他寿命预测模型之外[10],利用计算机的数值处理能力来研究滚刀磨损问题开始得到人们重视。徐玲等[11]将经过遗传算法(Genetic Algorithm, GA)优化过的反向传播(Back-Propagation,BP)神经网络应用于高速切削刀具的寿命预测中,解决了单纯应用BP神经网络时存在的收敛速度慢和过拟合等缺点,并通过刀具寿命预测实现了对切削参数的优化选择。李笑等[12]提出将Elman神经网络应用于盾构滚刀磨损量的预测,通过工程实际数据的训练和检验,得到了同类地质条件下的Elman神经网络盾构滚刀磨损寿命预测模型,拟合效果良好。以上研究表明,利用人工智能算法建立回归模型可以预测滚刀的磨损量,然而神经网络的弊端是会出现过拟合情况,所得结果往往是非全局最优解;又因神经网络模拟人类大脑的思维方式进行训练,无法得出显性的预测函数表达式,影响了工程应用的便捷性。
遗传规划(Genetic Programming, GP)在随机产生初始种群、形成算法搜索空间的基础上,运用进化论中适者生存与随机信息交叉原理,通过适应度指导的非线性搜索得出最适应研究对象的函数表达式。GP无需人为选择预测函数的结构类型和组成要素,摆脱了以往经验的影响,还可以自动生成和寻找函数关系[13-14]来体现各影响因素与预测目标之间的变化规律,适合针对众多影响因素之间复杂关系的研究。鉴此,本文根据复杂地层中盾构掘进时滚刀磨损量较大,并且其寿命难以预测的复杂性特点,将GP应用于复杂地层中盾构滚刀磨损寿命预测,建立了基于GP的盾构滚刀磨损寿命预测模型。该模型通过GP将磨损寿命预测问题转化为程序的归纳问题,通过树状函数表达式可反映出在复杂地质条件下滚刀寿命影响因素与磨损寿命之间的关系。工程实例和简化的CSM模型的计算结果验证了该模型的可行性。
1 遗传规划及可行性验证
1.1 遗传规划
遗传规划是1989年美国学者R.K. John对遗传算法进行延伸和扩展后提出的一种创造性的全局寻优技术。遗传规划随机生成的初始解通过复制、交换、突变等遗传操作不断迭代进化并自动寻找最优解[15],可以更好地适应复杂工况下各影响因素与磨损量之间的高度非线性关系,能发现和反映问题实质并灵活地表达最优解。
1.2 遗传规划计算流程
1.2.1 函数集的选取
待确定函数集由n个终止符(x1,x2,…,xn)和m个函数(f1,f2,…,fm)构成。本例中终止符xi为复杂地层中滚刀磨损寿命的各主要影响因素。函数集类型fi示例如下:
(1) 算术运算符,如+,-,×,/等。
(2) 数学标准函数,如sin,cos,log,exp等。
(3) 条件表达式,如If-then-else,Switch-Case等。
(4) 布尔运算,如AND,OR,NOT等。
(5) 控制转移说明语句,如Goto,Call,Jump等。
(6) 循环表达式,如Do-until,While-do,For-do等。
(7) 其他可定义函数。
1.2.2 生成初始群体
以随机组合的方式将基本元素组合成为初始个体,初始个体达到规定数目之后组成初始群体。个体树根节点为程序在函数集F={f1,f2,…,fn}中按照均匀分布的方式随机选取的某一个函数。选择根节点的目的是为了产生一个复杂的、层次化的函数结构,因而无需人为选择预测函数的结构类型和组成要素,无需研究者对磨损规律有太深的研究,摆脱了以往经验的影响。
1.2.3 适应度与进化方式
(1) 适应度:进化计算过程中自然选择的驱动力被称为适应度,充当控制器的作用。适应度值越小,则个体越优良。个体对环境的适应能力可以通过多种方式来进行度量,原始适应度是其中之一。在群体中,子代t中某一个个体i的原始适应度r(i,t)定义为
(1)
式中:A(i,j)为个体i在适应度计算实例j下的返回值;Ni为适应度计算代数;C(j)为j的实测值。
(2) 个体的进化方式:主要有复制、交叉和突变。本文所采用的个体复制选择方法是适应度比例选择法,也就是个体适应度值越高,那么被选中的概率就越大。个体被选中的概率为
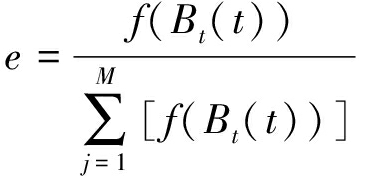
(2)
式中:f(Bt(t))为个体Bt(t)在第t代的适应度;M为群体中的个体数目。
交叉是主要的进化方式。交叉操作如图1所示。交叉操作根据原始适应度选择方法从群体中将第1代亲体选出,第2代亲体也以同样方式选出,但两者选择过程独立。2个亲代个体通过部分相互替代,形成2个新的个体。其中“1,2,3,4”为亲代1的4个终止符;“a,b,c,d,e”为亲代2的5个终止符。
突变时,亲代的突变点是树的函数点,删除突变点以下的子树,随机生成一棵子树插入突变点。突变如图2所示,其中1—5为终止符。
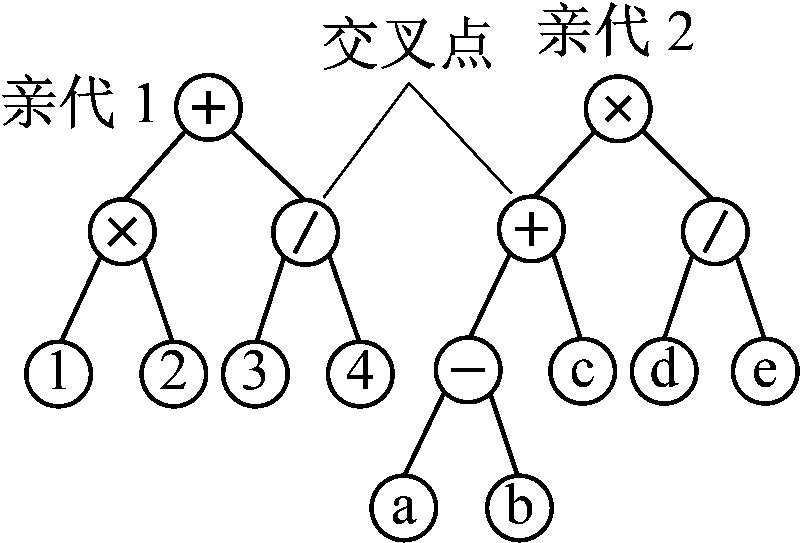
(a) 交叉前
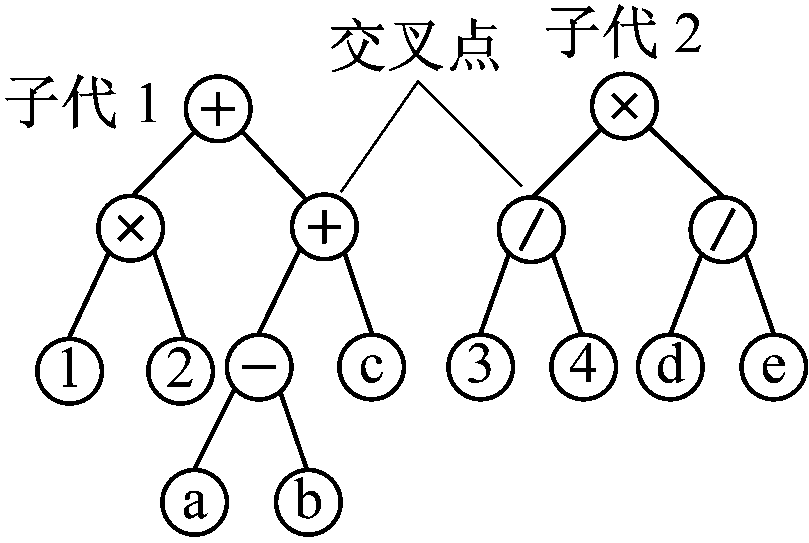
(b) 交叉后
图1 交叉
Fig.1 The graph of crossover
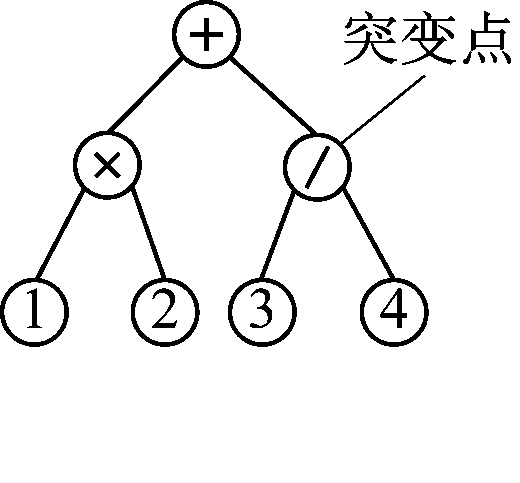
(a) 突变前
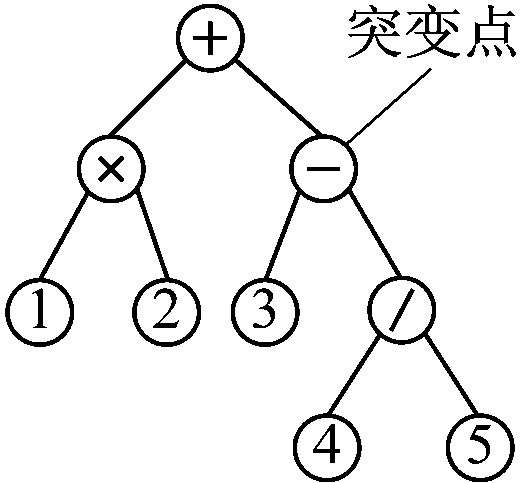
(b) 突变后
图2 突变
Fig.2 The graph of mutation
1.2.4 终止准则与结果输出
一旦GP输出值满足设定的终止准则,进化过程应立刻终止。本文采用的终止准则:当运行进化到允许误差之内或达到最大树深时终止迭代。结果标定方法是选择出一个全局最佳个体。一旦终止规则满足,则进化终止,当前计算机缓冲区中的个体就作为全局最佳个体进行输出[16-17]。
本文所用遗传规划流程如图3所示。
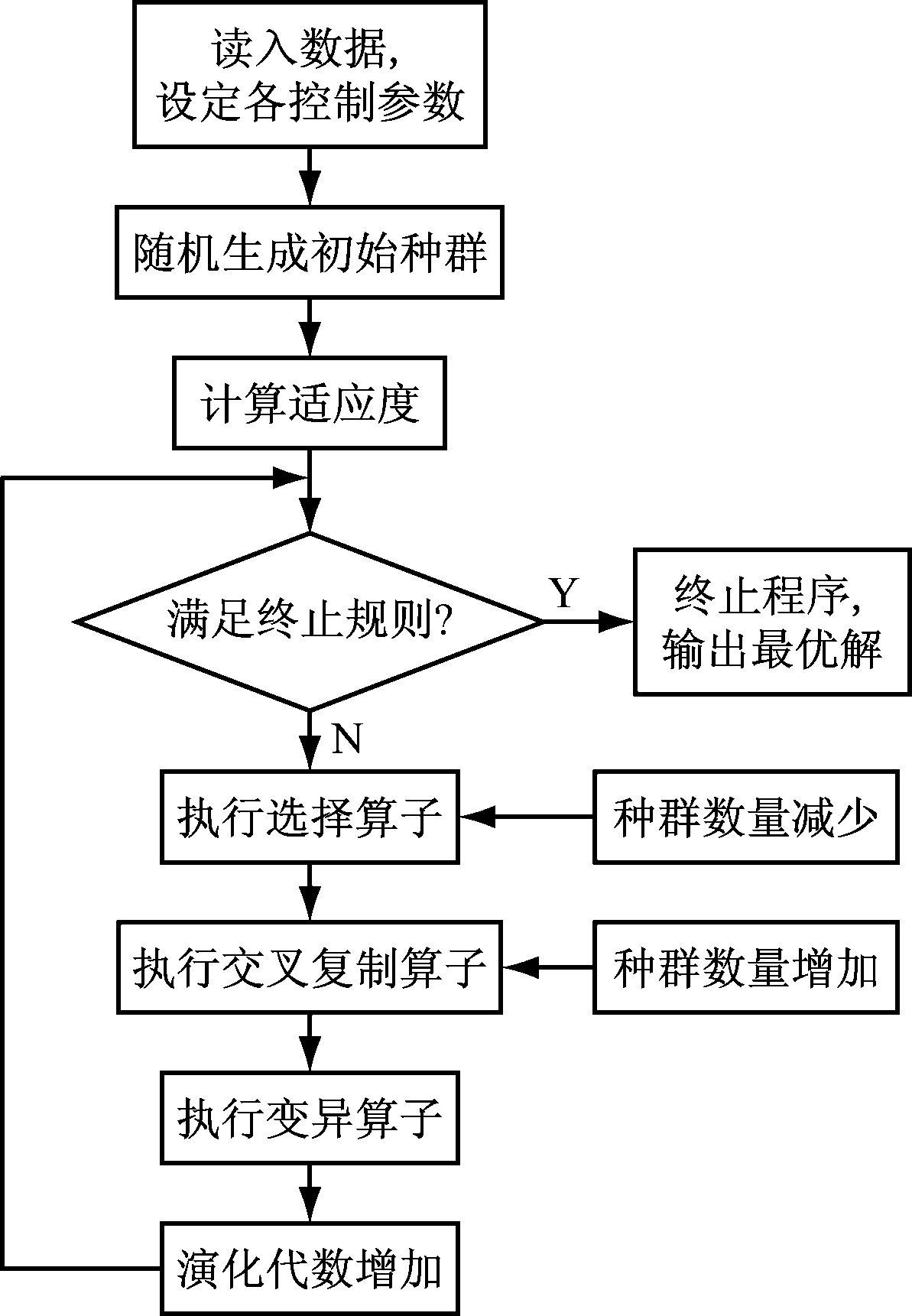
图3 遗传规划流程
Fig.3 Flow of genetic programming
1.3 遗传规划非线性回归的可行性验证
1.3.1 准备工作
为验证遗传规划对于非线性函数的解决能力和初步确定函数集,首先对给定实验函数![]() 进行程序可行性验证。使用Matlab作为实验平台编制遗传规划程序[18-19],用20组示例样本(表1)对程序进行训练。表1中,x1,x2为输入,Y为输出。选取适合的基本参数[20],GP模型参数设置见表2,运行程序并以返回的方差的大小对结果进行衡量。
进行程序可行性验证。使用Matlab作为实验平台编制遗传规划程序[18-19],用20组示例样本(表1)对程序进行训练。表1中,x1,x2为输入,Y为输出。选取适合的基本参数[20],GP模型参数设置见表2,运行程序并以返回的方差的大小对结果进行衡量。
表1 测试的数据样本
Table 1 Testing data samples
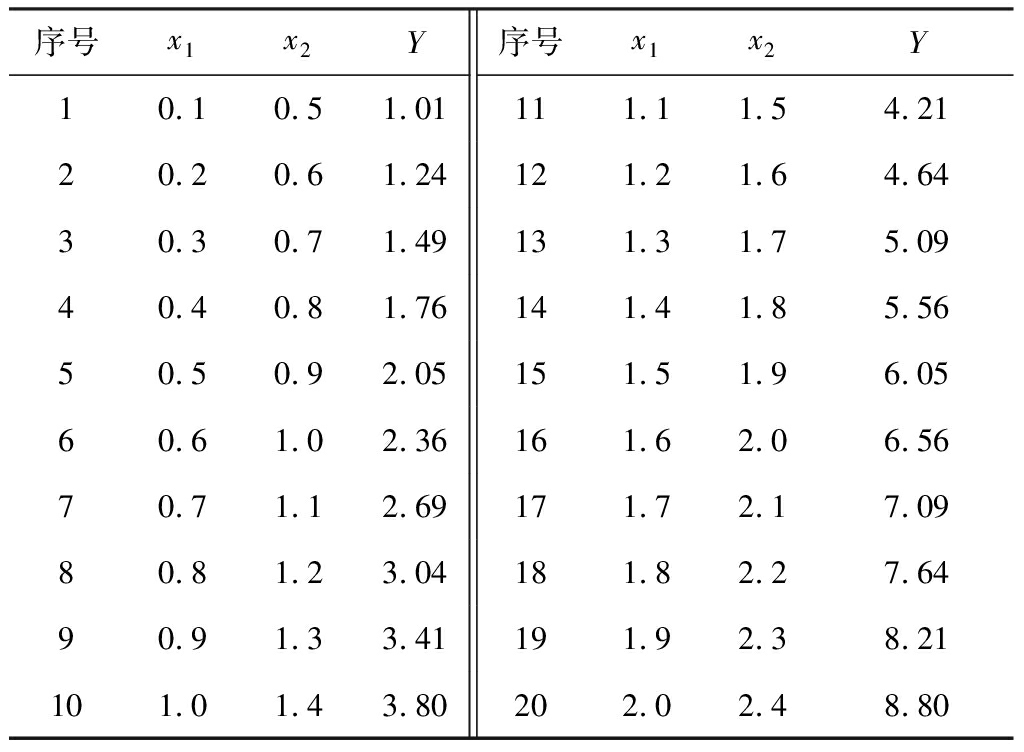
表2 GP模型参数设置
Table 2 Setting parameter of GP model

1.3.2 输出结果
适应度优化过程和树状表达式如图4、图5所示。从图4可以看出,初始种群的适应度值为15.673,进化一代之后,适应度值下降到6.920 3。随着进化代数的增加,训练样本和检验样本的方差逐代减小,第9代时得到了最佳适应度(适应度为0)的个体。化简该树状图可得![]() 真实地反映了函数关系表达式。可见,在表达式未知的情况下使用GP拟合非线性问题是可行的。
真实地反映了函数关系表达式。可见,在表达式未知的情况下使用GP拟合非线性问题是可行的。
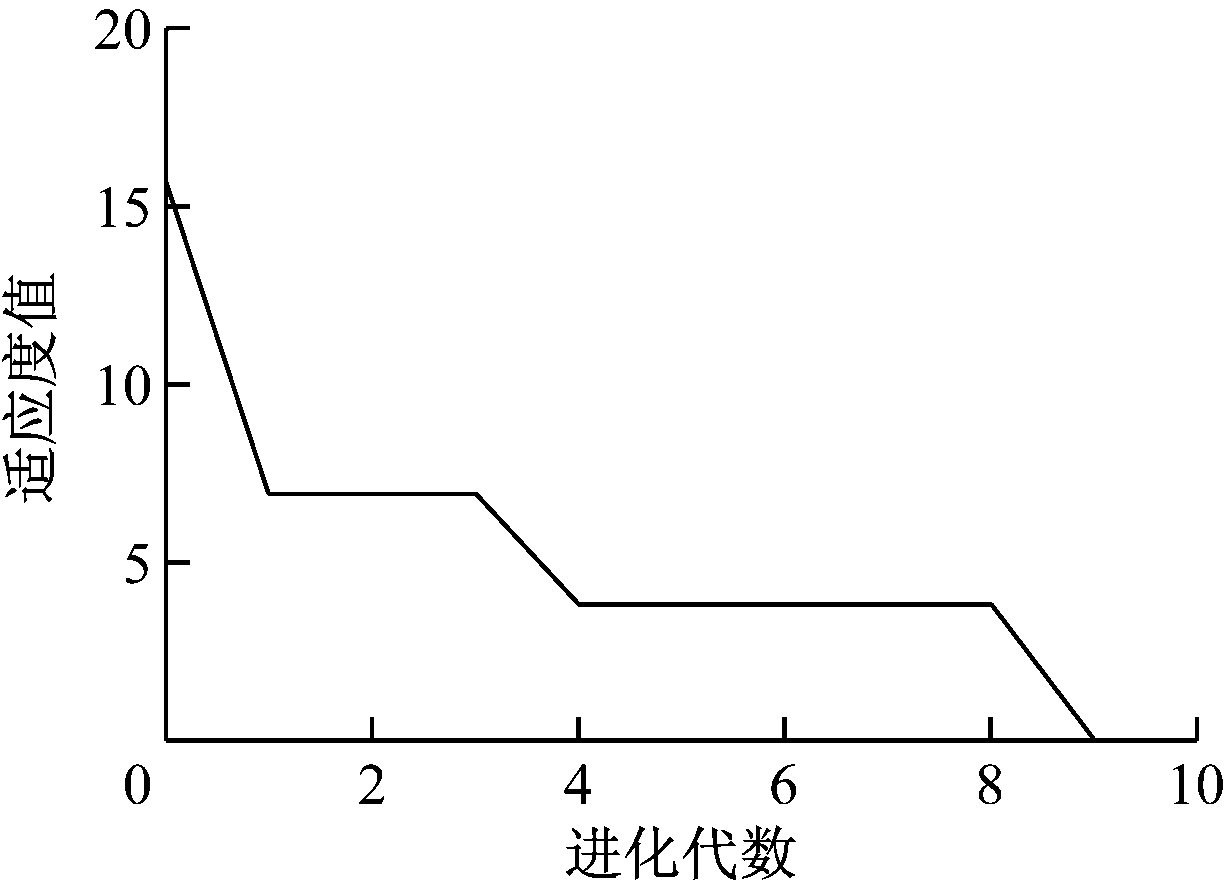
图4 适应度优化过程
Fig.4 Fitness optimization process
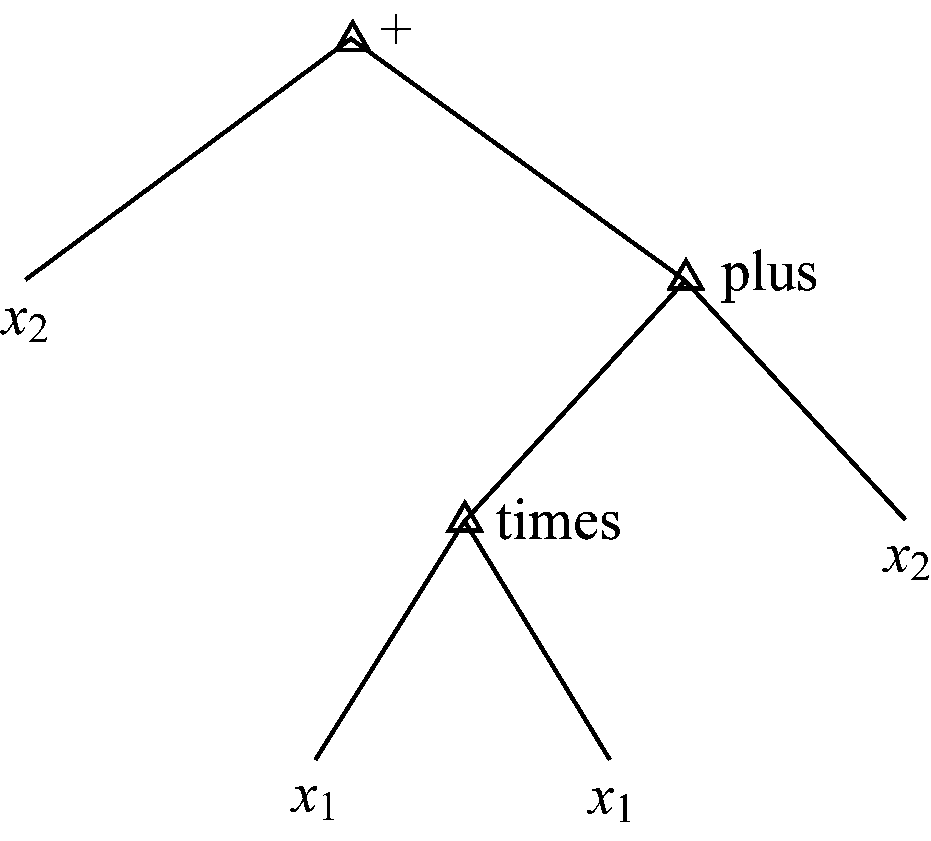
图5 遗传规划结果树状表达式
Fig.5 Tree-shaped expression of GP
2 基于遗传规划的复杂地层中盾构滚刀磨损寿命预测模型
2.1 工程概况
本文以某砂卵石地层盾构开挖工程为研究对象[21]。该工程采用12.04 m盾构机,初装刀盘是开口率为30%的复合式刀盘,滚刀直径均为431.8 mm。穿越地层主要以砂卵石为主,最大粒径为650 mm,在地下水位变化带存在1~2 m的砂卵石胶结层,取样得其最大强度可达23 MPa。掘进区间的地层可分3种:第1种地层以粉质黏土为主,另加粉土和粉、细砂,约占4.7%;第2种地层主要为砂层及圆烁、卵石土层,约占0.10%;第3种地层以卵石土、圆砾、土为主,另加中砂、粗砂、粉质黏土和粉土,占95.20%。局部地段穿越几种地层交杂的复杂地层段并长距离富水。以3次换刀磨损测量值作为训练数据。由于砂卵石地层中刀具受力复杂,砾石冲撞和偏磨作用使得非正常磨损占有一定比例,训练模型前应去除。整理后的径向累计磨损量X与安装半径R的关系如图6所示,滚刀编号和安装半径见表3。
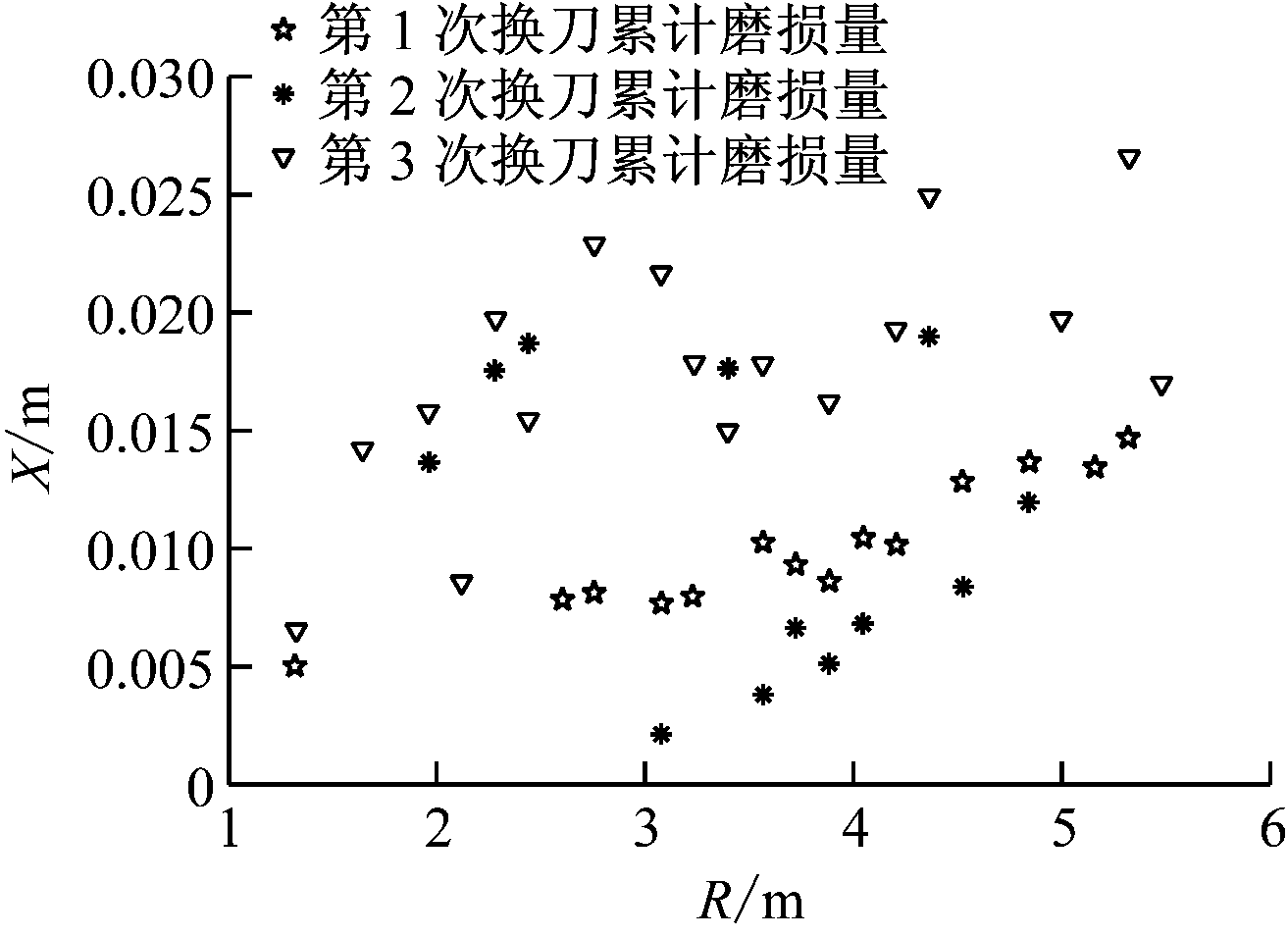
图6 滚刀径向累计磨损量与安装半径的关系
Fig.6 Relation between cumulative wear and installation radius of disc cutter
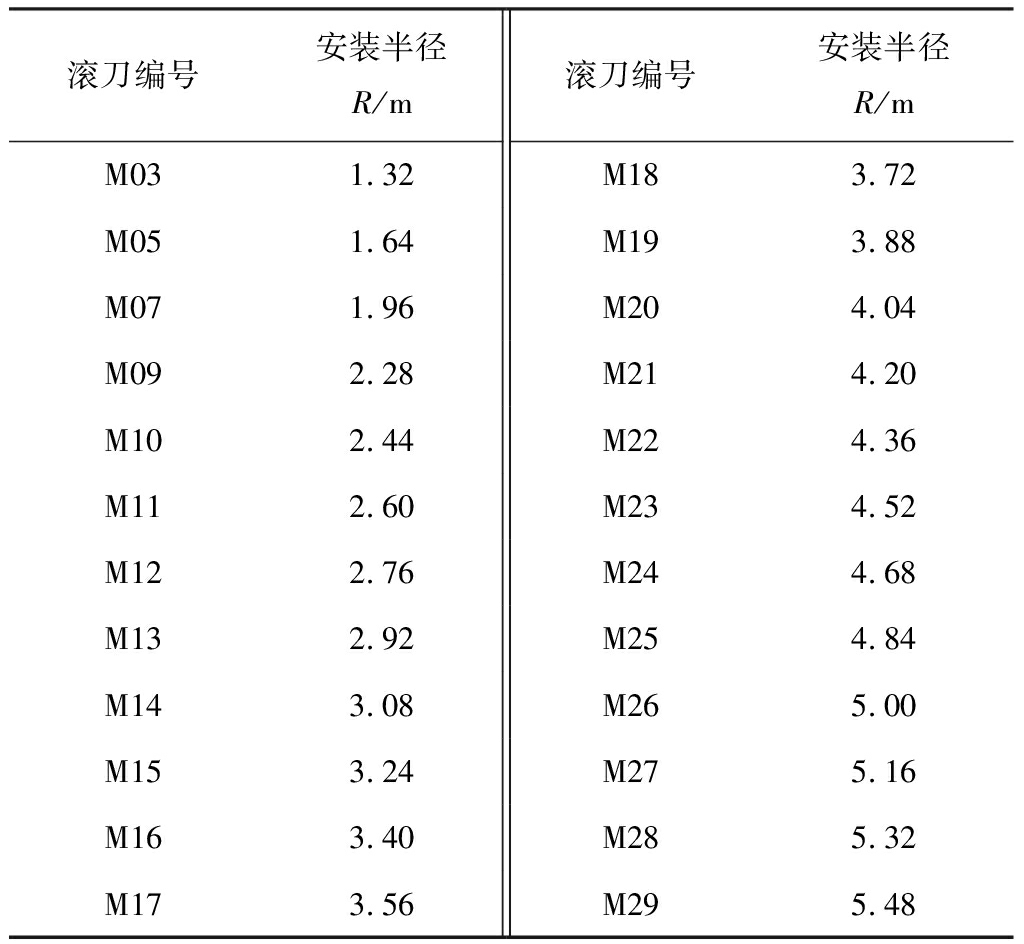
表3 滚刀编号和安装半径
Table 3 Disc cutter numbering and installation radius
2.2 基于遗传规划的滚刀磨损寿命预测
2.2.1 主要影响因素
在盾构机械参数相同时,滚刀磨损量与地质参数、掘进参数密切相关。由于复杂地层中各地层的强度、研磨性等均对滚刀磨损有直接影响,本文仅以某砂卵石地层为例对基于遗传规划的滚刀磨损寿命预测的可行性进行研讨。
滚刀磨损寿命主要影响因素包括滚刀安装半径和掘进参数,掘进参数又包括掘进距离、刀具贯入度、刀间距、刀盘转速及掘进推力等。
(1) 安装半径:在掘进距离相同的情况下,滚刀掘进轨迹与安装半径成正比,故滚刀磨损量与安装半径成正比[21]。
(2) 掘进距离:衡量磨损量不可缺少的影响因素之一。在滚刀对岩土进行切削时会产生大量可磨蚀滚刀的渣土,随着距离延长,岩渣与滚刀接触时间增加,是加快滚刀磨损的重要因素。
(3) 贯入度:由磨粒磨损理论可知,贯入度和滚刀的磨损量之间的关系为正相关[2]。当采用小贯入度掘进时,同样的掘进距离需要更多的刀盘转动圈数,增加了岩石与刀圈相对滑动的摩擦耗能,并最终导致磨损量的增加。
(4) 刀间距:刀间距的大小决定着开挖面岩土块的剥离形式,是影响掘进的重要参数。不同的刀间距会导致碎石体积不同,引起磨损机理的变化,影响滚刀正常磨损和非正常磨损的比例。
(5) 刀盘转速:转速较高时,同时间段内滚刀掘进距离延长,同时增加了工作面的摩擦作用,从而产生热量,导致刀圈温度提高、金属材料回火,进而降低表面强度,促进磨损进一步发生。此外,高温条件会加速刀圈氧化,加剧对滚刀材料的腐蚀。刀盘转速与滚刀磨损量成正比。
2.2.2 预测模型建立
首先,根据所研究的问题确定终止符集合。由上文可知,本工程实例中作为输入变量的5个主要影响因素为:x1:安装半径R,m;x2:掘进距离L,m;x3:贯入度h,m/rev;x4:刀间距S,m;x5:刀盘转速N,r/min,再加上一个临时随机常数J,可得终止符集:T={x1,x2,x3,x4,x5,J}。本问题函数集可定义为F={+,-,×,/,sin,cos,exp,mylog}。其中,每个函数所需的自变量个数为2,2,2,2,1,1,1,1。
从图6中的43组实测值中抽取滚刀编号为奇数的10组数据作为检验样本(表4),其余33组数据代入GP程序中作为训练样本。这里采用实测值的组数作为适应度示例值,即33个。原始适应度定义为实测值与返回值的绝对误差的平均值。
当计算个体的适应度值时,如果实测值与返回值的差小于某一事先给定的精度要求,该个体得1分。故终止条件:至少有一个个体的得分等于33,或迭代次数达到最大代次。最后,找出当前代中适应度最好的个体作为问题的解。
GP在复杂地层中滚刀磨损寿命预测中的主要参数是在考虑计算节约机时的基础上,根据多次试验确定的。设定终止准则:个体树嵌套深度达到32或迭代次数达到最大设定值。对于群体规模和最大迭代次数的设定宜由小到大尝试,使计算所得的适应度值最小,即拟合效果最好。经测试后确定模型参数设置,见表5。其中mylog函数是指当子树的值H等于0时,函数返回0,当子树的值H不等于0时,返回log(abs(H))。具体算法如下:
(1) 生成初始群体。在模型的函数集F和终止符集T中,对函数集类型fi和终止符xi进行随机组合,构成群体规模为40的初始群体。初始群体中的个体是随机生成的个体树。生成个体树时,首先从函数集F中随机地选取一个f0作为个体树的树根。根据函数f0所需自变量的数目1~2,产生1~2条辐射线。接着从函数集和终止符的并集中随机选取一个元素作为每条辐射线的节点,若终止符被选作为节点,则该点就成为树的终止生长的点,也称为叶子节点;若辐射线的节点选择的是一个函数,就按上述过程递归地继续生长,直到所有辐射线的节点均为叶子节点。
表4 检测样本
Table 4 Testing samples
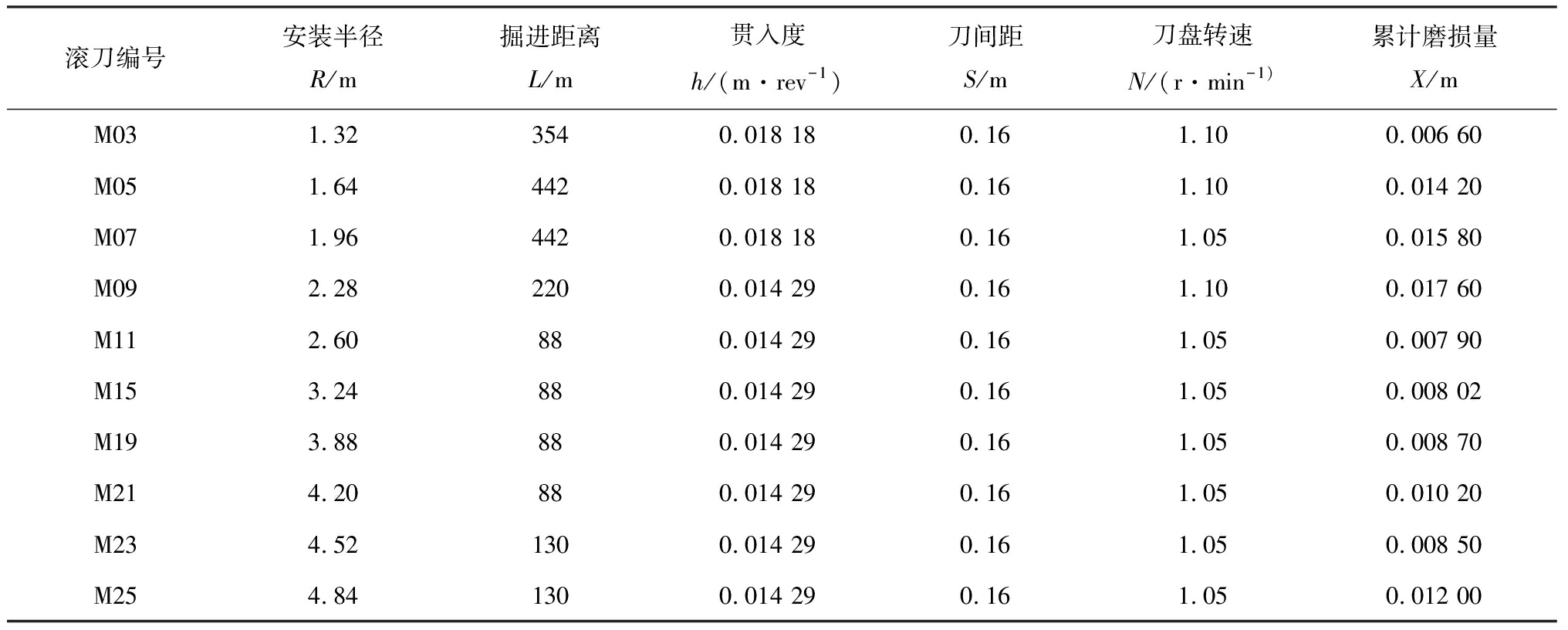
表5 基于GP的复杂地层中盾构滚刀磨损寿命预测模型的参数设置
Table 5 Setting parameter of shield disc cutter wear life prediction model in complex formations based on GP

(2) 计算所生成的个体树的适应度值。
(3) 根据适应度的选择方式,从群体中选出适应度较好的个体,即亲代。对亲代进行复制、交叉、变异等遗传操作,生成一个子代群体,通过淘汰适应度值低的个体,保持群体规模不变。
重复步骤(2)、步骤(3),直到满足设定的终止规则。计算进化达到25代时结束,并将终止前进化所得的最后一代作为全局最优个体输出,得到遗传规划的最佳个体树(图7),所得函数关系式转换为式(3)。
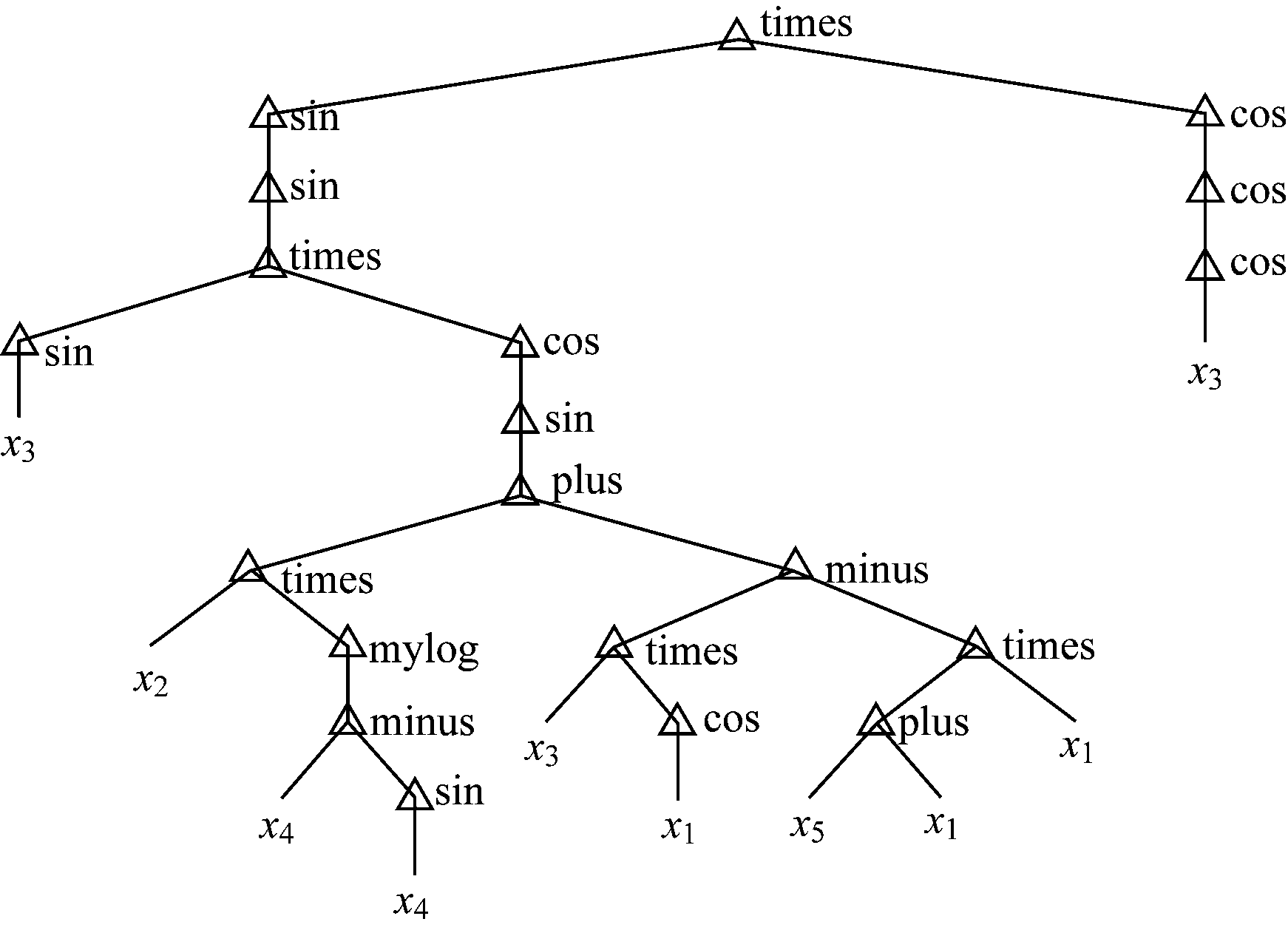
图7 GP的最佳个体树
Fig.7 Best individual tree obtained by GP model
X1=sin(sin(sin (h)cos(sin((L×mylog(S-sin (S)))+((hcos (R))-((N+R)×R))))))×cos(cos(cos(h)))
(3)
式(3)即为基于GP的复杂地层中盾构滚刀磨损寿命预测模型。
3 实验验证
3.1 简化CSM磨损预测模型与遗传规划模型验证
科罗拉多矿业大学基于室内滚刀破岩实验得来的CSM模型在目前的工程中应用广泛。利用文献[10,22]中的CSM滚刀磨损寿命预测模型进行相近参数的简化可得
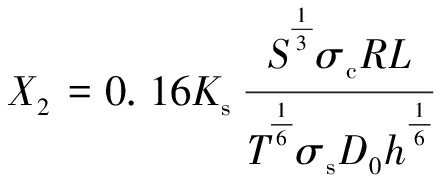
(4)
式中:X2为掘进距离L后的滚刀径向累计磨损量;Ks为磨粒磨损系数;σc为岩石单轴抗压强度;σs为刀刃屈服强度;T为滚刀的刀刃宽度;D0为刀直径。
根据式(4)计算正常磨损量。参数设置如下:刀间距S为0.16 m,刀直径D0为0.431 8 m,刀刃宽度T取0.02 m,刀刃屈服强度σs取149 4 MPa,岩石单轴抗压强度σc取地层的均值11.25 MPa。第1、2次换刀的贯入度为0.0142 9 m/rev,第3次换刀的贯入度为0.018 18 m/rev。由于岩石对钢制滚刀的磨损为三体磨损,磨粒直径为80 μm左右[2],故Ks为4×10-3。
3.2 结果对比分析
将测试样本(表4)分别代入式(3)中的基于GP的复杂地层中盾构滚刀磨损寿命预测模型(以下简称GP预测模型)和式(4)中的简化CSM磨损预测模型并计算出寿命预测结果(图8),分别计算平均误差和均方差(表6),以评定所建模型的精度。
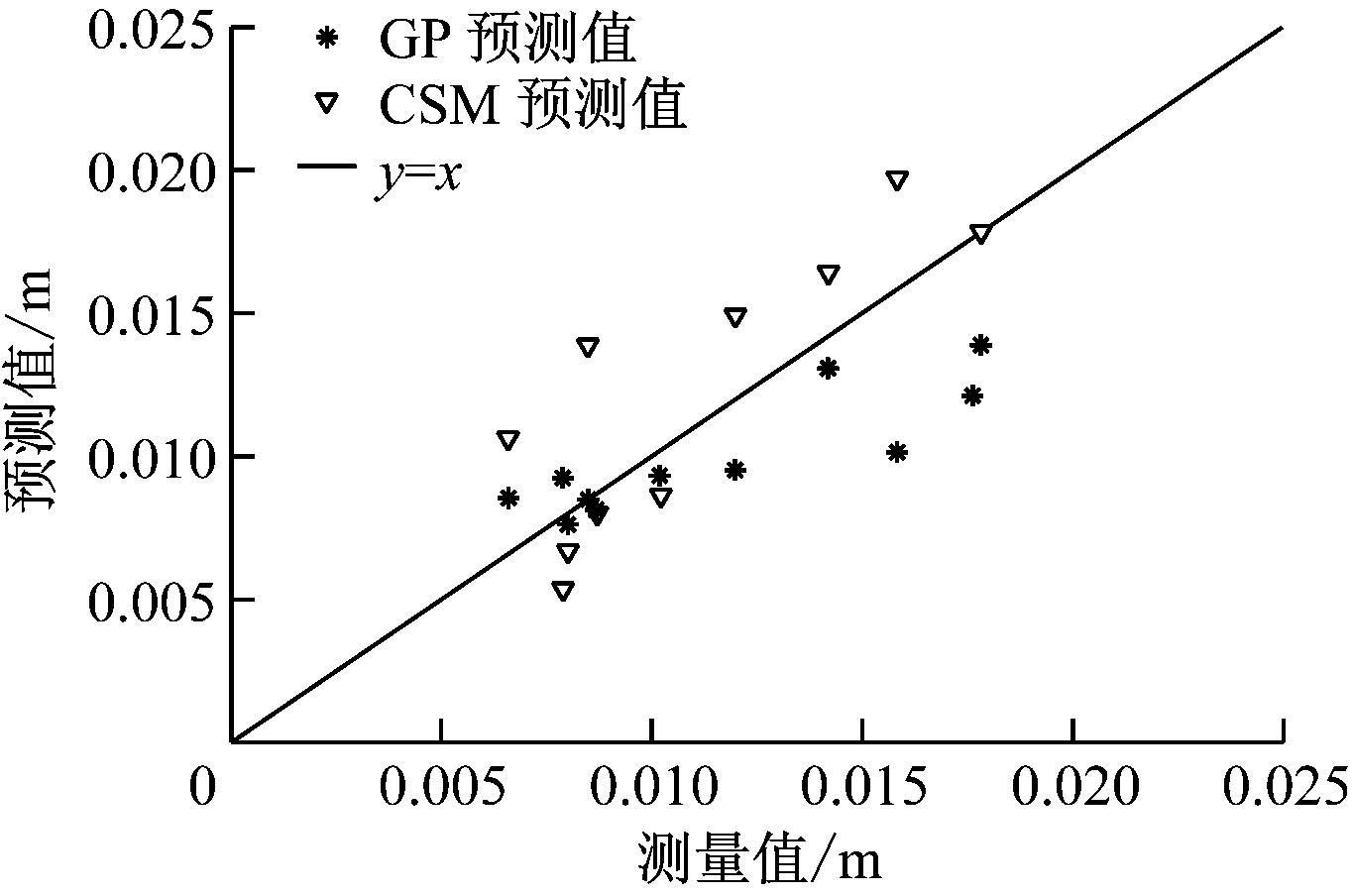
图8 2种滚刀磨损寿命预测模型的预测值与测量值对比
Fig.8 Comparison between the predicted values and the measured values of two cutter wear life prediction models
表6 2种模型拟合精度比较
Table 6 Comparison of fitting precisions of the two models
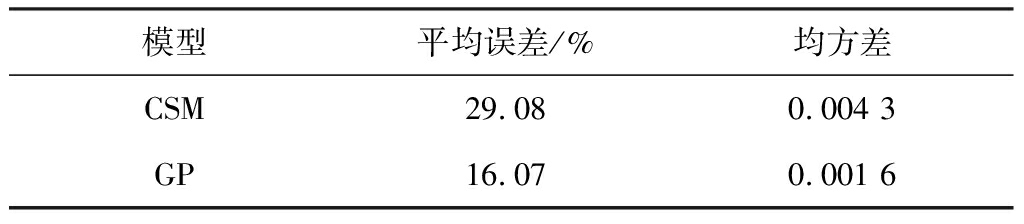
从结果的偏离程度可知,2种模型的总体趋势与实际情况相同。简化CSM磨损预测模型中参数取值的准确与否是影响滚刀磨损寿命预测精度的关键问题,但岩石单轴抗压强度σc等参数却由于复杂地层的不均匀性难以测得准确值,因而计算偏差相对较大。GP预测模型在复杂地层中计算出的拟合值比较理想地反映了滚刀磨损规律,精度明显优于前者,成功解决了具有高度非线性特点的盾构滚刀寿命的预测问题。
4 结论
(1) 在对影响滚刀磨损寿命的各主要影响因素进行合理分析和选择的基础上,将遗传规划引入到滚刀磨损寿命预测中,建立了基于遗传规划的复杂地层中盾构滚刀磨损寿命预测模型。利用工程实例的实测数据进行模型训练,并用测试的工程实例数据和简化CSM磨损预测模型进行验证,结果表明,该模型平均误差小、均方差小。
(2) 基于遗传规划的复杂地层中盾构滚刀磨损寿命预测模型通过个体树和函数表达式的形式表达结果,更为直观,能更好地预测复杂地质条件下的滚刀磨损寿命,达到了减少停机检查的次数、加快施工效率和减少工程成本的目的,为盾构滚刀磨损寿命的分析和预测开辟了一条新的途径。
参考文献(References):
[1] 赵海鸣,舒标,夏毅敏,等.基于磨料磨损的TBM滚刀磨损预测研究[J].铁道科学与工程学报,2014,11(4):152-158.
ZHAO Haiming,SHU Biao,XIA Yimin,et al.Study of wear prediction for TBM cutter based on abrasive wear model[J].Journal of Railway Science and Engineering,2014,11(4):152-158.
[2] 孙汝继,王水生,王海舰.掘进机截齿磨损程度分析及识别方法[J].工矿自动化,2016,42(12):68-71.
SUN Ruji,WANG Shuisheng,WANG Haijian.Analysis and recognition method of wear degree of roadheader cutting picks[J].Industry and Mine Automation,2016,42(12):68-71.
[3] BALCI C.Correlation of rock cutting tests with field performance of a TBM in a highly fractured rock formation: a case study in Kozyatagi-Kadikoy metro tunnel,Turkey[J].Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research,2009,24(4):423-435.
[4] WIJK G.A model of tunnel boring machine performance[J].Geotechnical & Geological Engineering,1992,10(1):19-40.
[5] ROSTAMI J.Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D].Colorado: Colorado School of Mines,1997.
[6] BRULAND A.Hard rock tunnel boring advance rate and cutter wear[R].Trondheim: Norwegian Institute of Technology,1999.
[7] 龚秋明,王继敏,佘祺锐.锦屏二级水电站1#,3#引水隧洞TBM施工预测与施工效果对比分析[J].岩石力学与工程学报,2011,30(8):1652-1662.
GONG Qiuming,WANG Jimin,SHE Qirui.Comparison of TBM performance prediction with actual TBM operation results in headrace tunnels No.1 and No.3 of Jinping II hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(8):1652-1662.
[8] OIHCMB M,SCHMID L,RITZ W,et al.Hardrock tunnel boring machines[M].Ernst & Sohn,2008.
[9] ROSTAMI J,OZDEMIR L,NILSEN B.Comparison between CMS and NTH hard rock TBM performance prediction models[C]//Annual Technical Meeting of the Institute of Shaft Drilling and Technology (ISDT),1996:1-11.
[10] 杨延栋,陈馈,李凤远,等.盘形滚刀磨损预测模型[J].煤炭学报,2015,40(6):1290-1296.
YANG Yandong,CHEN Kui,LI Fengyuan,et al.Wear prediction model of disc cutter[J].Journal of China Coal Society,2015,40(6):1290-1296.
[11] 徐玲,杨丹,王时龙,等.基于进化神经网络的刀具寿命预测[J].计算机集成制造系统,2008,14(1):167-171.
XU Ling,YANG Dan,WANG Shilong,et al.Prediction of cutting tool life based on evolutionary neural network[J].Computer Integrated Manufacturing Systems,2008,14(1):167-171.
[12] 李笑,苏小江.基于Elman神经网络的盾构滚刀磨损预测方法研究[J].辽宁工程技术大学学报(自然科学版),2010,29(6):1121-1124.
LI Xiao,SU Xiaojiang.A new method for forecasting shield disc-cutters wearing based on Elman neural network[J].Journal of Liaoning Technical University (Natural Science),2010,29(6):1121-1124.
[13] 乔金丽,张义同,谢晓晖.基于遗传规划的盾构隧道开挖地表最大沉降预测[J].天津大学学报,2009,42(9):790-795.
QIAO Jinli,ZHANG Yitong,XIE Xiaohui.Genetic programming approach to predicting the maximum surface settlement by shield tunneling[J].Journal of Tianjin University,2009,42(9):790-795.
[14] 赵黎丽.两种人工智能方法应用于地热热泵系统辨识[J].系统仿真学报,2004,16(7):1376-1379.
ZHAO Lili.Two artificial intelligent methods applied in the identification of geothermal heat pump system[J].Journal of System Simulation,2004,16(7):1376-1379.
[15] 李书全,李敏强,寇纪淞,等.遗传规划及其在地基设计中的应用[J].系统工程学报,1997,12(4):87-91.
LI Shuquan,LI Minqiang,KOU Jisong,et al.Gentic programming and it's application[J].Journal of System Engineering,1997,12(4):86-91.
[16] 云庆夏,黄光球,王战权.遗传算法和遗传规划——一种搜索寻优技术[M].北京:冶金工业出版社,1997.
[17] 云庆夏,卢少华.优化地下采矿方法结构的遗传规划[J].化工矿物与加工,2001,20(2):13-17.
YUN Qingxia,LU Shaohua.Genetic programming for the structural optimization of underground mining methods[J].Industrial Minerals and Processing,2001,20(2):13-17.
[18] KOZA J R.Genetic programming:on the programming of computers by means of natural selection[M].Cambridge:MIT Press,1992.
[19] SILVA S,COSTA E.Dynamic limits for bloat control:variations on size and depth[J].Lecture Notes in Computer Science,2004,3103:666-677.
[20] 翟淑花,高谦.遗传规划在最大下沉值预测中的应用[J].煤炭学报,2007,32(3):239-242.
ZHAI Shuhua,GAO Qian.Application of genetic programming on predicting maximum surface subsidence due to mining[J].Journal of China Coal Society,2007,32(3):239-242.
[21] 彭钧.复杂地层盾构刀具磨损控制技术研究[D].北京:北京交通大学,2013.
[22] 曾锋,苏华友,宋天田.复杂地层中盾构机滚刀寿命预测研究[J].地下空间与工程学报,2016,12(增刊2):755-759.
ZENG Feng,SU Huayou,SONG Tiantian.Research on service life prediction for disc cutters of shield machines in complex ground[J].Chinese Journal of Underground Space and Engineering,2016,12(S2):755-759.