0 引言
矿用变频器广泛应用于煤矿企业采、掘、运、通等过程,其性能优劣直接关系到煤机装备的安全稳定运行[1-2]。在无速度传感器条件下,变频器调速性能与异步电动机参数密切相关,而电动机厂家提供的铭牌参数仅表现了电动机的外部特性,因此,需要基于变频器逆变电路获取电动机内部参数[3-4]。
异步电动机参数辨识方法可分为在线辨识和离线辨识。离线辨识是在电动机投入运行之前,在电动机静止及空载状态下预先辨识参数。在线辨识是在电动机运行状态下进行参数测量和计算[5-6]。在线辨识依赖于离线辨识获得的电动机初始模型,且负载的扰动影响辨识准确性,因此,仅作为离线辨识的补充,在实际应用中仍需针对不同负载进行不断验证和改进[7-8]。离线辨识采用瞬态响应法测量漏感和转子电阻,采用稳态响应法测量定子电阻、自感和互感,避免了负载扰动的影响,是目前矿用变频器产品采用的主要参数辨识方式。目前对离线辨识方法的研究不断完善,如考虑铁损、电流的趋肤效应、死区时间、逆变电路器件压降及非线性特性等影响[9-10],然而,现有方法大多采用快速傅里叶变换等计算电流幅值和相位,存在频谱泄漏和栅栏效应,易导致测量误差。
针对上述问题,本文基于两电平三相逆变电路,将电动机等效电路作为负载,用PWM(脉冲宽度调制)信号控制IGBT(绝缘栅双极型晶体管),从而控制负载端激励电压,通过电流传感器检测定子电流,计算定子电阻、转子电阻、定转子互感、漏感等参数,实现异步电动机参数离线辨识。
1 异步电动机等效电路
异步电动机一相绕组等效电路如图1所示,其中us为定子电压,R1为定子电阻,Lσ1为定子漏感,Lσ2为转子漏感,R2为转子电阻,Lm为定转子互感,s为转差率。该等效电路将转子侧参数折算到定子侧[11]。电动机参数辨识在该等效电路的基础上实现。
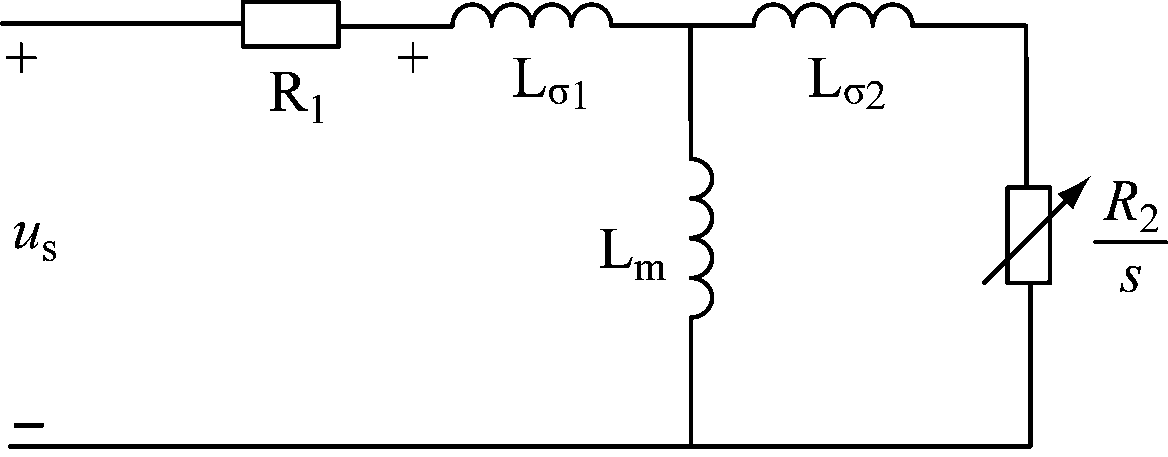
图1 异步电动机一相绕组等效电路
Fig.1 Equivalent circuit of one-phase winding of asynchronous motor
2 异步电动机参数辨识方法
2.1 定子电阻辨识方法
基于稳态响应法,通过直流试验进行定子电阻辨识。通过PWM信号控制逆变电路,在任意一相与另外一相或两相绕组之间施加一定的等效直流电压,检测绕组电流,计算出定子电阻[12]。当两相之间施加直流电压时,定转子互感、漏感相当于被短接,单相等效电路和实测时的两相等效电路如图2所示。其中uuv为U相和V相之间施加的定子电压,Is为定子电流,Ru,Rv,Rw为三相等效定子电阻。测试期间W相上下桥臂一直处于关断状态,W相定子电阻处于悬空状态。

(a)单相等效电路

(b)两相等效电路
图2 定子电阻辨识等效电路
Fig.2 Equivalent circuit of stator resistance identification
当直流电压施加到定子侧时,相当于直流母线电压udc经过逆变器开关器件和定子电阻形成回路[13]。U相和V相之间施加的电压uuv波形如图3所示,其中t为时间,D为占空比,ta为调制载波周期。在0~Dta时间段内,U相上桥臂导通、下桥臂关断,V相上桥臂关断、下桥臂导通,uuv=udc;在Dta~ta时间段内,U相上桥臂关断、下桥臂导通,V相上桥臂导通、下桥臂关断,uuv=-udc。
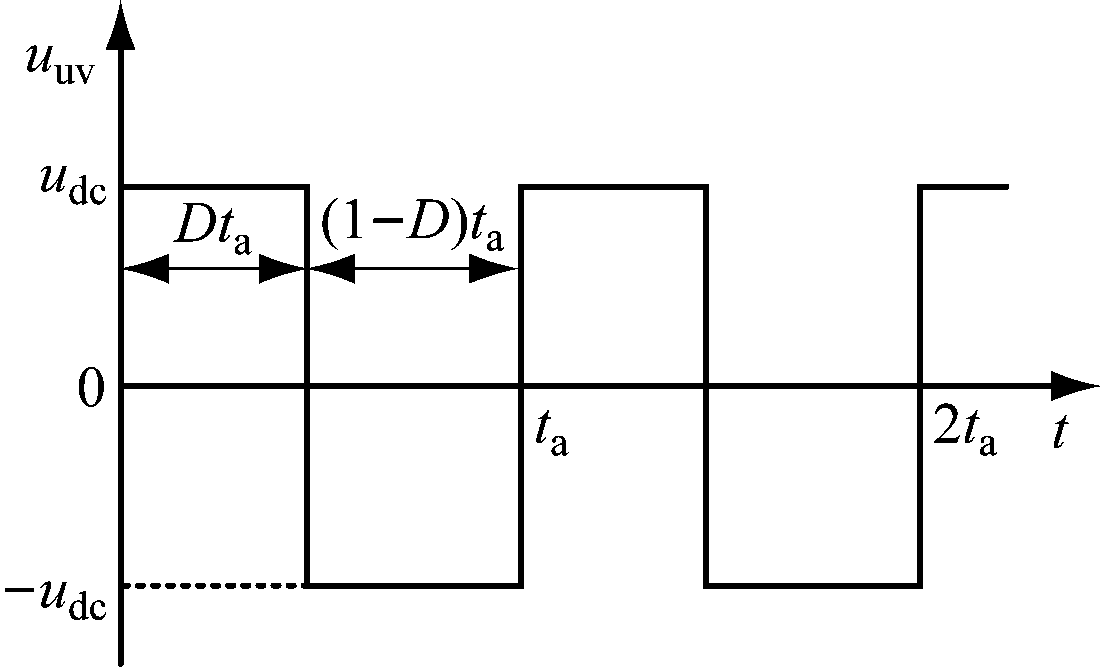
图3 定子电阻辨识过程中的电动机电压波形
Fig.3 Motor voltage waveform during stator resistance identification
由图3可知,输出等效直流电压u满足如下关系:
udcDta+(1-D)ta(-udc)=uta
(1)
u=(2D-1)udc
(2)
结合图2和式(2)可得
u=IsR1
(3)
(4)
通过控制PWM信号的占空比调节输出电压,从而调节定子电流。由式(2)可知,若占空比D由50%开始向上调节,则输出等效直流电压由0开始增大,电动机电流随之逐渐增大。在Matlab/Simulink仿真环境下,按照上述方法在定子侧施加直流电压并调节,得到定子电流响应波形,如图4所示。可见,稳态时U相电流和V相电流大小相等、极性相反。
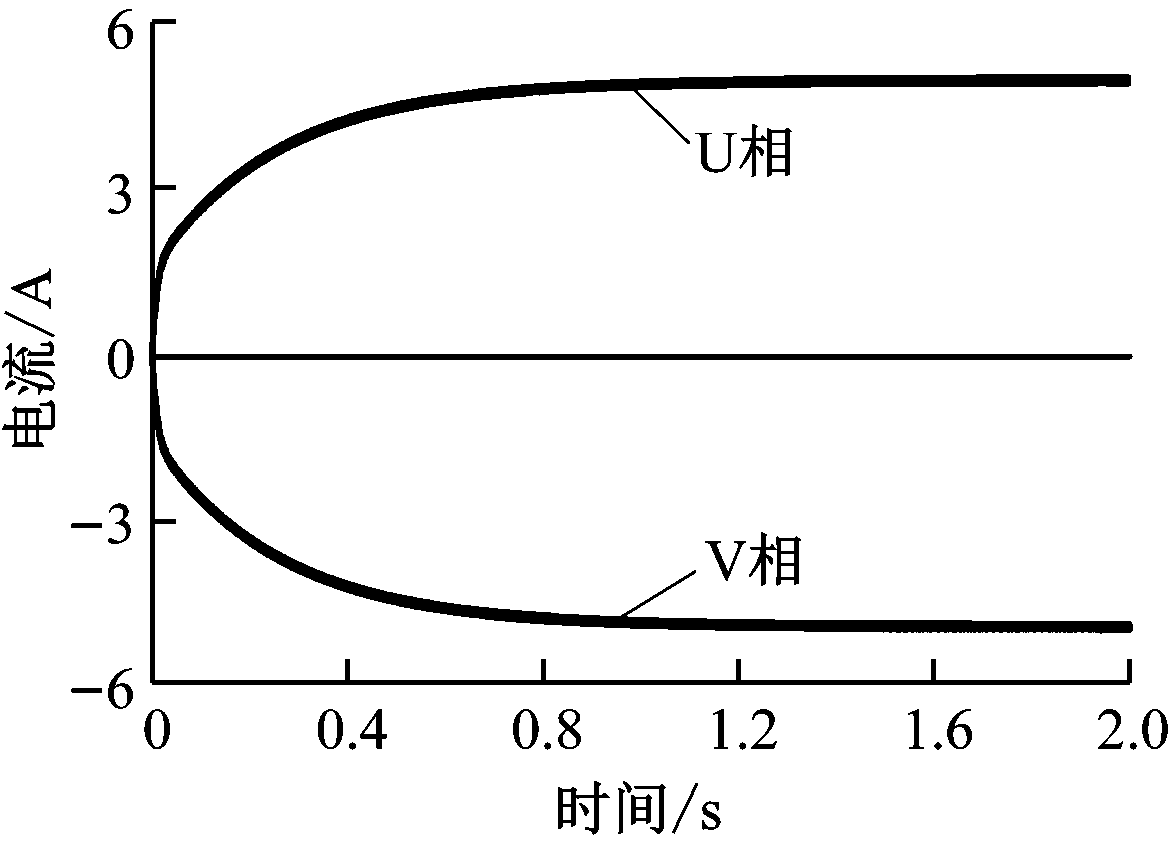
图4 定子电阻辨识过程中的电流响应波形
Fig.4 Current response waveform during stator resistance identification
为了保证异步电动机的安全,同时使定子电流在可准确测量的范围内,调节等效直流电压,使电动机定子电流分别达到100%,150%电动机额定电流。设定子电流达到100%电动机额定电流时的占空比为D1,使占空比固定不变,多次采样直流母线电压并求取平均值udc1,多次采样电动机定子电流并求取平均值i1。同理可得定子电流达到150%电动机额定电流时对应的占空比D2、直流母线电压平均值udc2、电动机定子电流平均值i2。将2次输出电压差值与2次电流差值的比值作为实际的定子电阻值:
(5)
与采用单次采样值直接计算的方式相比,采用2次采样值差值计算的方式可减小因逆变器IGBT器件压降引起的测量误差[3]。
2.2 转子电阻和漏感辨识方法
2.2.1 方法原理
由图1可知,当通入角频率为ω的交流电压时,互感抗为
ZLm=ωLm
(6)
当通入方波阶跃电压时,理想状态下,阶跃瞬间电压交流分量角频率ω为无穷大,则互感抗ZLm为无穷大,此时电动机单相等效电路如图5(a)所示。控制逆变电路U相上桥臂IGBT器件开通和关断,V相和W相下桥臂IGBT器件始终处于开通状态,此时电动机等效电路如图5(b)所示。互感相当于开路,因此,电动机没有电磁转矩,与堵转的情况相同。此时定转子漏感之和为Lσ=Lσ1+Lσ2,定转子电阻之和为R=R1+R2,则电动机三相阻抗Zu,Zv,Zw为
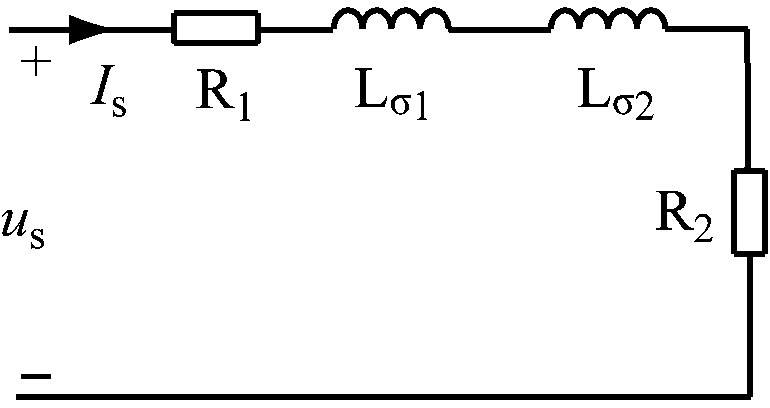
(a)单相等效电路

(b)三相等效电路
图5 转子电阻和漏感辨识等效电路
Fig.5 Equivalent circuit of rotor resistance and leakage inductance identification
Zu=Zv=Zw=R+jωLσ
(7)
由图5可知,在等效电路中,单相总阻抗Z的电压uz为

(8)
由式(7)和式(8)可得
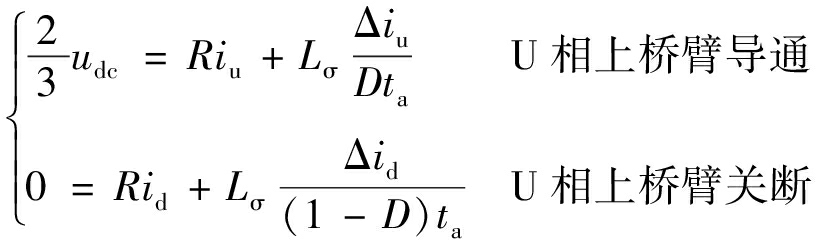
(9)
式中:iu为施加电压后等效电路中的直流电流,取2次电流测量值的平均值;Δiu为施加电压后等效电路中的电流变化量,取2次电流测量值的差值;id为施加的电压断开后等效电路中的直流电流,取2次电流测量值的平均值;Δid为施加的电压断开后等效电路中的电流变化量,取2次电流测量值的差值。
通常认为定转子漏感相等,则有

(10)
式(9)中,udc可通过仿真环境获得,占空比D和载波周期ta可由仿真调节过程得到。进行转子电阻和漏感辨识时,每次发出N个PWM波,获得2N个采样电流值In,n为采样次数。根据采样电流值可求得Δiu,Δid,iu,id:
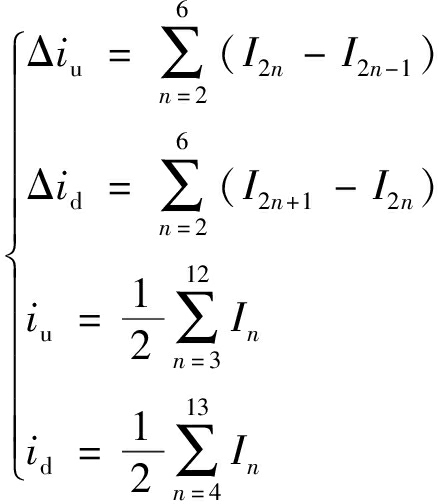
(11)
将式(11)代入式(9)、式(10),求得1组转子电阻和漏感。求取多组转子电阻和漏感,去掉最大值和最小值,求平均值,得到最终的转子电阻和漏感。
2.2.2 仿真验证
通过Matlab/Simulink平台对上述方法进行仿真验证。异步电动机模型参数如下:电动机功率P=2.2 kW,额定电压为380 V,定子电阻R1=3.92 Ω,定转子漏感Lσ1=Lσ2=11.90 mH,互感Lm=215.87 mH,转子电阻R2=1.52 Ω。
仿真时,控制器连续按组发出PWM波,每组7个脉冲。在电感储能作用下,每组第7个脉冲发出时,电动机电流达到峰值。调节占空比,使电流峰值达到电动机额定电流后,保持占空比恒定,对电压、电流进行采样并计算转子电阻和漏感。占空比恒定后,定子电压波形和电流响应波形如图6所示。

(a)电压波形

(b)电流波形
图6 转子电阻和漏感辨识过程中的电压和电流波形
Fig.6 Voltage and current waveforms during rotor resistance and leakage inductance identification
转子电阻和漏感辨识的1组仿真采样数据见表1,一共获取6组数据,每组14次采样,组与组之间间隔80 ms。结合采样数据,通过转子电阻和漏感辨识方法求得转子电阻R2≈1.50 Ω,定子漏感Lσ1≈11.80 mH,与Matlab/Simulink给定的电动机模型参数相符,验证了转子电阻和漏感辨识方法的准确性。
表1 转子电阻和漏感辨识仿真采样数据
Table 1 Sampling data of rotor resistance and leakage inductance identification simulation A

I0I1I2I3I4I5I602.7501.7324.0762.0314.7052.344I7I8I9I10I11I12I135.0122.4975.1452.5515.2382.5945.251
2.3 定转子互感辨识方法
进行三相异步电动机恒压频比空载实验时,电动机转速接近同步转速,转差率s近似等于0,转子电流近似等于0,可认为转子侧开路。定转子互感辨识等效电路如图7所示[14]。
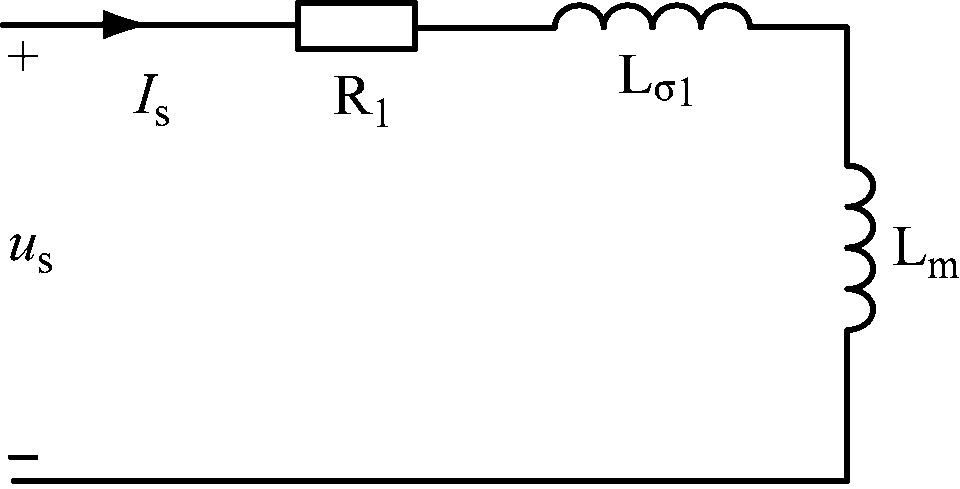
图7 定转子互感辨识等效电路
Fig.7 Equivalent circuit for mutual inductance identification of stator and rotor
三相异步电动机通入三相交流电压信号,使异步电动机在额定频率下旋转。等效电路中互感Lm和定子总电感L、定子漏感Lσ1的关系为
Lm=L-Lσ1
(12)
在恒压频比模式下,逆变电路通过SVPWM调制输出三相对称的等效正弦电压,电动机定子将产生旋转磁场,因此与同步旋转坐标系下的异步电动机模型相符[15]。根据图7可得到M-T同步旋转坐标系下的异步电动机电压、电流如图8所示,其中ISM,IST分别为定子电流矢量Is在M轴、T轴方向的分量。

图8 同步旋转坐标系下异步电动机电压、电流相量图
Fig.8 Voltage and current phasor diagram of asynchronous motor in synchronous rotating coordinate system
M-T坐标系和电压矢量us以正弦信号角频率ω旋转,若取T轴参考方向与电压矢量us参考方向相同,将电压矢量us分解为平行于Is的电压矢量u2和垂直于Is的电压矢量u1,则有
![]()
(13)
式中θ为功率因数角。
空载电流Is为空载状态下采样的定子电流信号,由式(13)可得电动机定子总电感:
(14)
在计算出漏感数据的基础上,结合式(12),可求得异步电动机定转子互感Lm。
3 电动机参数辨识结果验证
3.1 电动机参数辨识实验
一般实验室采用市电供电,由于电源容量所限,验证平台上的电动机功率为2.2 kW,因此,前期验证采用380 V/2.2 kW三相异步电动机。搭建380 V/2.2 kW变频器机芯,对参数辨识方法的准确性进行初步验证。
2.2 kW电动机参数辨识过程中的电压波形如图9所示。定子电流采用2 000∶1霍尔电流传感器测量,通过400 Ω采样电阻上的分压来反映。定子电压采用高压差分衰减探头直接测量,示波器已经调整探头衰减比例,图中定子电压幅值为实际值。

(a)定子电阻辨识波形

(b)转子电阻和漏感辨识波形

(c)定转子互感辨识波形
图9 2.2 kW电动机参数辨识过程中的电压波形
Fig.9 Voltage waveforms during parameter identification of 2.2 kW motor
在异步电动机参数辨识过程中,变频器施加给电动机的电压信号得到了正确的电流响应,与仿真结果一致。
实测2.2 kW电动机完整参数见表2。由偏差情况可知,测量过程可重复性较好,辨识结果是收敛的。
表2 实测2.2 kW电动机完整参数
Table 2 Measured complete parameters of 2.2 kW motor

组别R1/ΩR2/ΩLm/mHLσ1/mH13.7320.924230.66.6023.8170.883229.36.5733.8000.920229.96.6343.8260.907231.26.6153.8080.895230.26.58平均值3.7970.906230.26.60偏差1.71%2.54%0.43%0.45%
3.2 电动机参数辨识和变频器控制效果
搭建660 V/90 kW矿用变频器机芯,采用本文提出的参数辨识方法进行参数辨识,将辨识出的电动机参数输入变频器矢量控制软件,验证能否达到整机性能指标要求。矿用变频器机芯和性能测试平台如图10所示。

(a)矿用变频器机芯

(b)性能测试平台
图10 矿用变频器机芯及性能测试平台
Fig.10 Chip and performance test platform of mine inverter
实测90 kW电动机完整参数见表3。将该参数作为矢量控制算法的常量,用于电流解耦和励磁、转矩闭环控制。
表3 实测90 kW电动机完整参数
Table 3 Measured complete parameters of 90 kW motor

组别R1/mΩR2/mΩLm/mHLσ1/mH152.6236.5040.811.49252.5436.5340.871.48352.7036.4840.901.48452.9936.4540.921.49552.7836.5340.991.49平均值52.7336.5040.901.49偏差0.49%0.14%0.22%0.67%
变频器控制电动机在100%额定转矩下带载启动并达到稳定运行状态,电动机转速、转矩、输出频率和电流波形如图11所示。转矩、转速通过加载系统的转矩、转速传感器测量,输出频率、电流通过电能质量分析仪测量。电动机启动成功后持续输出额定转矩并运行30 min,变频器加速到额定转速的时间为30 s,为了体现带载启动时的低频转矩输出能力,仅记录前32 s启动过程。为了观测方便,将输出频率曲线放大10倍显示。由图11可知,将辨识出的电动机参数用于矿用变频器矢量控制系统,变频器能够在额定转矩下带载启动并持续稳定运行。

图11 电动机转速、转矩、输出频率和电流波形
Fig.11 Motor speed, torque, output frequency and current waveforms
4 结论
(1)基于稳态响应法,通过直流试验进行定子电阻辨识。采用2次采样值差值计算的方式得到定子电阻,与采用单次采样值直接计算的方式相比,可减小因逆变器IGBT器件压降引起的测量误差。
(2)采用瞬态响应法辨识转子电阻和漏感,Matlab/Simulink仿真结果表明,转子电阻和漏感参数辨识结果与给定的电动机模型参数相符,验证了参数辨识方法的准确性。
(3)建立同步旋转坐标系下的电动机模型,在恒压频比空载运行状态下,对电流瞬时值进行旋转坐标变换,计算电流幅值和相位,进而辨识定转子互感和空载励磁电流。
(4)实验及测试结果表明,电动机参数辨识过程可重复性较好,辨识精度较高,可满足矿用变频器矢量控制要求。
[1] 荣相.矿用变频器性能测试系统设计[J].工矿自动化,2021,47(5):9-15.
RONG Xiang.Design of mine inverter performance test system[J].Industry and Mine Automation,2021,47(5):9-15.
[2] 史晗,蒋德智,荣相,等.矿用变频器LRC滤波器寄生参数影响研究[J].工矿自动化,2020,46(8):44-50.
SHI Han,JIANG Dezhi,RONG Xiang,et al.Research on influence of parasitic parameters of LRC filter for mine-used inverter[J].Industry and Mine Automation,2020,46(8):44-50.
[3] 段亮,莫锦秋,曹家勇.基于变频器的异步电机离线参数辨识[J].电机与控制应用,2011,38(7):38-43.
DUAN Liang,MO Jinqiu,CAO Jiayong.An offline asynchronous motor's parameter identification method based on inverter[J].Electric Machines & Control Application,2011,38(7):38-43.
[4] 贺艳晖,王跃,王兆安.异步电机参数离线辨识改进算法[J].电工技术学报,2011,26(6):73-80.
HE Yanhui,WANG Yue,WANG Zhao'an.An improved off-line parameter identification algorithm for induction motors[J].Transactions of China Electrotechnical Society,2011,26(6):73-80.
[5] 周明磊,李强,游小杰,等.方波工况下牵引电机参数不准对矢量控制性能的影响[J].电机与控制学报,2014,18(2):42-49.
ZHOU Minglei,LI Qiang,YOU Xiaojie,et al.Influence of incorrect traction machine parameters on vector control performance under pulse mode modulation[J].Electric Machines and Control,2014,18(2):42-49.
[6] 周江华,万山明,华志超.感应电动机磁链观测与参数在线辨识方法研究[J].电机与控制应用,2018,45(11):72-77.
ZHOU Jianghua,WAN Shanming,HUA Zhichao.A study of flux linkage observation and online parameter identification for induction motor[J].Electric Machines & Control Application,2018,45(11):72-77.
[7] 杨淑英,孙瑞,曹朋朋,等.一种基于双复合滑模面滑模观测器的异步电机转子电阻辨识方案[J].电工技术学报,2018,33(15):3596-3606.
YANG Shuying,SUN Rui,CAO Pengpeng,et al.Double compound manifold sliding mode observer based rotor resistance online updating scheme for induction motor[J].Transactions of China Electrotechnical Society,2018,33(15):3596-3606.
[8] 陈振锋,钟彦儒,李洁.感应电机参数辨识三种智能算法的比较[J].电机与控制学报,2010,14(11):7-12.
CHEN Zhenfeng,ZHONG Yanru,LI Jie.Comparison of three intelligent optimization algorithms for parameter identification of induction motors[J].Electric Machines and Control,2010,14(11):7-12.
[9] 漆星,张倩.Actor-Critic框架下的数据驱动异步电机离线参数辨识方法[J].电工技术学报,2019,34(9):1875-1885.
QI Xing,ZHANG Qian.Data-driven induction motor parameters offline identification method based on Actor-Critic framework[J].Transactions of China Electrotechnical Society,2019,34(9):1875-1885.
[10] 佘致廷,郑勇,袁俊波,等.带定子电阻辨识的异步电机无速度传感器直接转矩控制[J].电气传动,2011,41(5):10-14.
SHE Zhiting,ZHENG Yong,YUAN Junbo,et al.Direct torque control of induction motor speed sensorless with stator resistance identification[J].Electric Drive,2011,41(5):10-14.
[11] 张虎,孙天硕.基于滤波算法的感应电动机参数离线辨识[J].电气传动,2016,46(10):3-7.
ZHANG Hu,SUN Tianshuo.Off-line parameter identification of induction motor based on filtering algorithm[J].Electric Drive,2016,46(10):3-7.
[12] 陈康平,曾岳南,李海波,等.基于TMS320F2812的异步电机参数离线辨识系统[J].电机与控制应用,2013,40(8):5-8.
CHEN Kangping,ZENG Yuenan,LI Haibo,et al.System of off-line parameter identification for AC motor based on TMS320F2812[J].Electric Machines & Control Application,2013,40(8):5-8.
[13] 王高林,商振,于泳,等.感应电动机参数离线辨识方法实验研究[J].微电机,2009,42(6):4-7.
WANG Gaolin,SHANG Zhen,YU Yong,et al.Research on off-line parameter identification for induction motor[J].Micromotors,2009,42(6):4-7.
[14] 崔连香.异步电机参数静态辨识[J].电机与控制应用,2013,40(12):39-41.
CUI Lianxiang.Static parameter identification of asynchronous motor[J].Electric Machines and Control Application,2013,40(12):39-41.
[15] 张赛.感应电机转速估算和参数离线辨识研究[D].武汉:华中科技大学,2013.
ZHANG Sai.Research of the speed estimation and off-line parameters identification of induction motor[D].Wuhan:Huazhong University of Science and Technology,2013.
