0 引言
目前,变频调速系统越来越多地应用于刮板输送机、采煤机等煤矿机械中[1-2]。传统的变频调速系统整流器采用二极管不控整流方案,由于二极管具有单向导电性,所以电动机制动时的能量无法回馈到电网,且需要额外增加泵升限制电路以消耗产生的再生电能,避免直流母线电压骤升,导致严重的发热和能量浪费,同时增大了变频调速系统体积[3]。
双PWM(Pulse Width Modulation,脉冲宽度调制)控制的变频调速系统具有能量可双向流动、功率因数高(接近单位功率因数)、谐波污染小、储能环节容量小、恒定直流电压控制等优势[3],已应用于煤矿机械中,具有代表性的有SL500型、MGTY300/730-1.1D型采煤机。双PWM 控制的变频调速系统整流器网侧需设置滤波器来抑制谐波电流。与传统的单L滤波器相比,LCL滤波器在实现相同滤波效果的前提下具有更小的电感量、更小的体积和更低的成本[4],更适用于井下中大功率应用场合。LCL滤波器固有的谐振特性可能导致系统不稳定,因此需采用有源或无源阻尼法[5]进行阻尼。现有的LCL滤波器设计方法不仅依赖经验,而且需要反复试凑才能找到合适的参数,效率较低,同时着重考虑使网侧电流达到谐波标准,对阻尼损耗问题考虑不足[6-8],可能导致器件发热,不适于在恶劣的煤矿井下环境中应用。
本文以矿用双PWM变频调速系统整流器的滤波器为研究对象,对其总电感、滤波电容、电感比、阻尼电阻等参数进行了优化设计,通过仿真和实验验证了设计的滤波器可保证变频调速系统具有较高的功率因数、较低的电流总谐波畸变率、较小的电感,有利于减小变频调速系统体积,降低成本。
1 双PWM变频调速系统原理
双PWM变频调速系统主电路如图1所示。该系统的整流器采用LCL滤波器来抑制网侧电流谐波,整流器和逆变器均采用PWM控制技术,无需增加额外装置即可实现能量的可控双向流动,从而使异步电动机工作于四象限。因此,该系统非常适用于刮板输送机、采煤机等设备,可灵活、自动调节设备转速和转向,达到节能降耗目的[9]。

图1 双PWM变频调速系统主电路
Fig.1 Main circuit of dual PWM variable frequency speed regulation system
与传统的变频调速系统相比,双PWM变频调速系统的整流器采用全控器件作为开关,替换了不可控的二极管;采用PWM控制策略,不仅能实现能量双向流动,而且具有较快的动态响应能力。系统处于整流状态时从电网吸收电能,处于逆变状态时向电网回馈电能[10]。
2 三相PWM整流器及LCL滤波器模型
带LCL滤波器的三相PWM 整流器主电路如图2 所示。uga,ugb,ugc为三相网侧电压;ua,ub,uc为三相整流器侧电压;i1a,i1b,i1c为三相整流器侧电流;i2a,i2b,i2c为三相网侧电流;ica,icb,icc为三相滤波电容电流;L1为整流器侧滤波电感;L2为网侧滤波电感;Cf为滤波电容;Rd为抑制谐振的阻尼电阻;C为直流侧稳压电容;udc为直流侧输出电压;RL为直流侧负载电阻。

图2 带LCL滤波器的三相PWM整流器主电路
Fig.2 Main circuit of three-phase PWM rectifier based on LCL filter
整流器侧电压可等效为开关频率次谐波电压和基波电压的叠加,则连接整流器和电网的LCL滤波器可等效为如图3(a)所示的基本等效模型。U1,Uh分别为整流器侧电压的基波成分和谐波成分;Ug为网侧等效相电压;I1为整流器侧谐波电流;I2为网侧谐波电流;Ic为滤波电容电流。
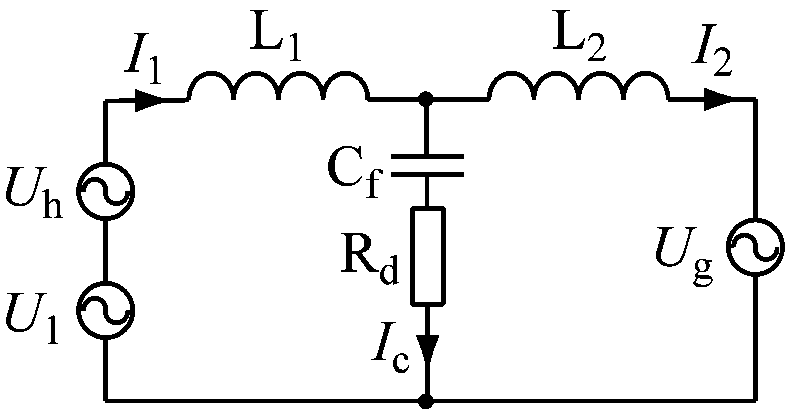
(a)基本等效模型

(b)高频等效模型
图3 LCL滤波器等效模型
Fig.3 Equivalent models of LCL filter
设计滤波器的主要目标是衰减Uh作为激励源而产生的I2,由此可得滤波器的高频等效模型,如图3(b)所示。定义电流衰减系数σ为网侧谐波电流和整流器侧谐波电流之比,则有

(1)
式中s为拉普拉斯算子。
令L2/L1=k(电感比),L1+L2=Lt(总电感),可得系统谐振频率:
(2)
阻尼电阻的加入增强了系统稳定性,同时也带来阻尼损耗问题[7],若不妥善处理,可导致系统效率和可靠性降低。因此,在保证系统稳定的前提下,阻尼电阻应尽可能小。
流过阻尼电阻的电流主要由开关频率次谐波电流、基波电流及谐振电流构成。由于滤波电容对基波的基频阻抗较大,对于流向电容的基波电流而言,阻容支路可看作开路,所以近似认为基波电流为零。因阻尼电阻对谐振峰有抑制作用,可近似认为谐振电流为零。因此,阻尼损耗绝大部分源于开关频率次谐波电流,即
(3)
式中:Ploss为阻尼损耗;Ihs为流过阻尼电阻的开关频率次谐波电流有效值。

(4)
式中ωhs为谐波角频率。
3 LCL滤波器参数优化
PWM整流器主要参数:额定功率为250 kW,直流侧输出电压为1 200 V,开关频率为5 kHz,三相线电压为690 V,电网频率为50 Hz。据此优化设计LCL滤波器参数。
3.1 总电感
LCL滤波器总电感除要求能够最大限度地抑制谐波电流外,还要满足电流快速跟踪和系统快速响应要求,由此可得总电感取值范围:
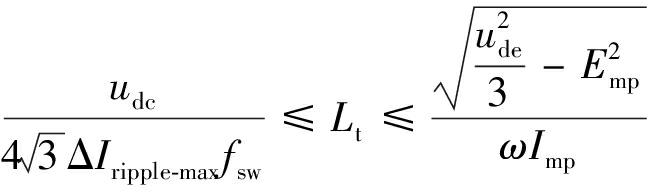
(5)
式中:ΔIripple-max为最大电流纹波;fsw为开关频率;ude为直流侧输出电压峰值;Emp为网侧相电压峰值;ω为电网角频率;Imp为网侧相电流峰值。
取允许最大电流纹波为相电流峰值的20%,则根据式(5)可得0.585 mH≤Lt≤4.34 mH。
LCL滤波器总电感越小,电流快速跟踪和系统快速响应能力越强;总电感越大,滤波效果越好。因此,需综合考虑,权衡选择合适值。井下应用场合一般要求整流器体积小,因此取Lt=0.6 mH。
3.2 滤波电容
滤波电容对低频信号呈高阻抗特性,对高频谐波呈低阻抗特性,因此可滤除大部分高频谐波。增大滤波电容可以更好地衰减谐波,但为了避免整流器功率因数过度降低,一般地,滤波电容上吸收的基波无功功率不超过系统额定有功功率的5%。本文取3%,即
(6)
式中PN为整流器额定有功功率。
将相关参数代入式(6),得Cf≤50.14 μF。通常滤波器中电感的磁芯部分占整个滤波器的大部分质量、体积和成本[11],设计时期望在满足滤波要求的情况下,尽量减少滤波器电感的磁芯材料。另外,电容制造工艺较成熟,滤波电容体积较小、成本低,在设计正确的前提下可减少滤波器故障[12]。因此,设计煤矿井下用LCL 滤波器时,在达到相同滤波效果的前提下,应尽量增大滤波电容以减小滤波器体积。本文取Cf=50 μF。
3.3 电感比和阻尼电阻
设计LCL滤波器时期望在保证良好滤波效果的基础上,最小化阻尼损耗,以降低发热。
阻尼电阻的加入使系统开环极点左移,增强了系统稳定性。一般地,阻尼电阻约为谐振频率下电容阻抗的1/3[13],即
(7)
3.3.1 电感比
取阻尼电阻为不同值,根据式(2)—式(4)绘制谐振频率fres、电流衰减系数σ和阻尼损耗Ploss关于电感比k的函数曲线,如图4所示。可看出:① fres关于k的函数曲线呈凹型,k=1时取最小值,根据10f0≤fres≤0.5fsw(f0为电网频率)的要求,k取值范围为(0.19, 3]。② 当阻尼电阻按式(7)取值时,σ在0<k≤1时呈快速下降趋势,k>1时下降趋势较平缓。为了尽可能衰减谐波,k应尽量大。③ Ploss随k增大呈单调增大趋势,且增速随k增大而增大。为降低损耗,k应尽量小。
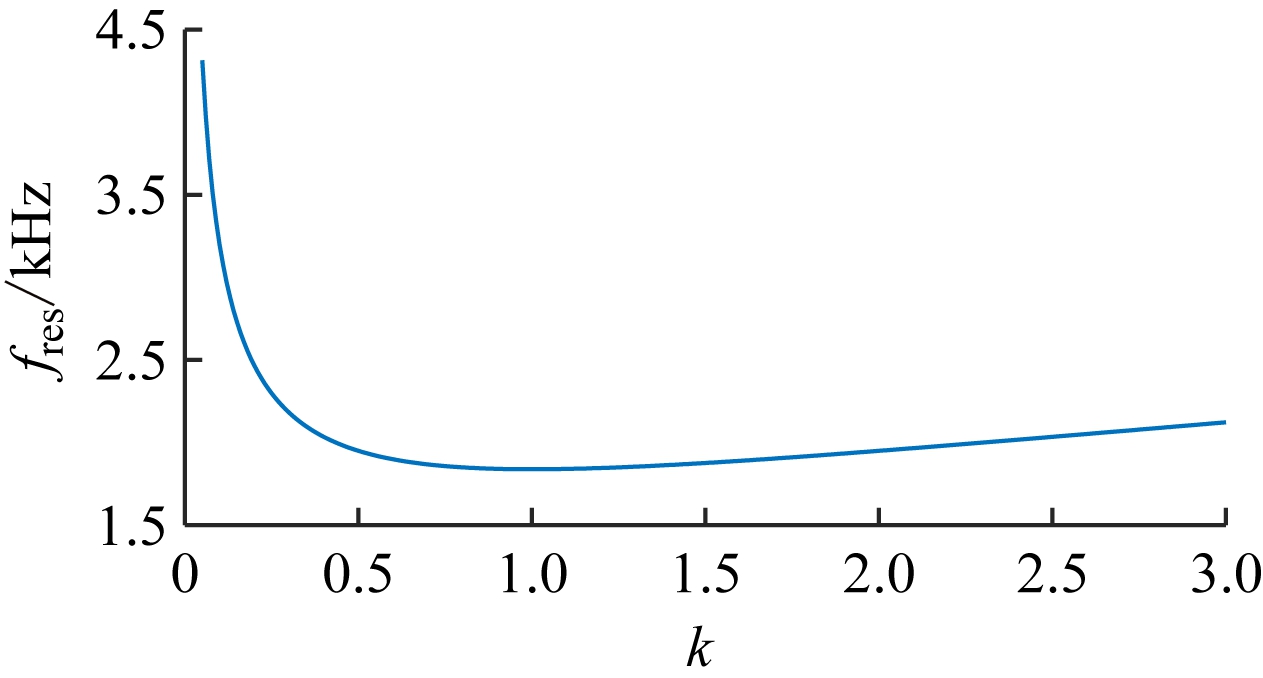
(a)谐振频率
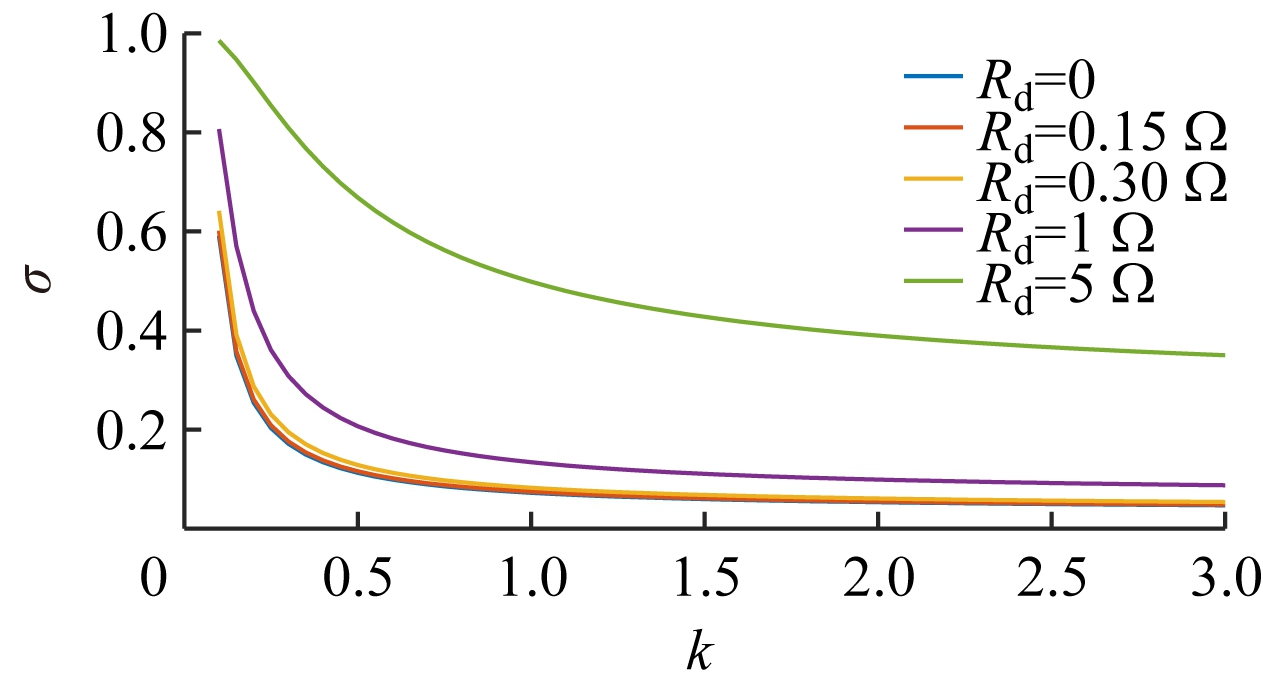
(b)电流衰减系数

(c)阻尼损耗
图4 谐振频率、电流衰减系数和阻尼损耗关于电感比的函数曲线
Fig.4 Function curves of resonant frequency, current attenuation coefficient and damping loss on inductance ratio
根据分析,若k∈(1,+∞],则k对σ的影响较小,但对Ploss影响很大,因此k取值范围为(0.19,1]。本文取k=0.2。
3.2.2 阻尼电阻
阻尼电阻的加入增加了LCL滤波器的阻尼,抑制了谐振峰。取不同的阻尼电阻,绘制滤波器开环传递函数伯德图,如图5所示。可看出:Rd=0时出现了较大的谐振峰,LCL滤波器不稳定;Rd=0.15 Ω时,谐振峰值在0附近,处于临界稳定状态;之后随着Rd增大,滤波器稳定裕度逐渐提高。

(a)幅值

(b)相角
图5 阻尼电阻不同时滤波器开环传递函数伯德图
Fig.5 Bode diagram of the filter's open loop transfer function under different damping resistances
阻尼电阻越大,滤波器开环传递函数的幅值裕度越大,越有利于稳定性控制,但存在因阻尼损耗引发的严重发热和高频谐波衰减能力不足问题,而阻尼电阻过小会导致系统不稳定。因此,优化设计的目标是找到比较合适的阻尼电阻,既能保证系统稳定,又能满足控制要求,降低阻尼损耗。
分别令k=0.2,0.4,0.7,1.0,绘制电流衰减系数σ和阻尼损耗Ploss关于阻尼电阻Rd的函数曲线,如图6所示。可看出:① σ随Rd增大呈单调增大趋势,且增大趋势随Rd增大而趋于平缓。为了尽可能衰减谐波,Rd应尽量小。② Ploss随Rd增大呈先增大后减小趋势。k=0.2时,Ploss关于Rd的函数曲线有1个拐点(Rd=A),Ploss在该点取极大值。为降低损耗,Rd应趋于零或无穷大。

(a)电流衰减系数
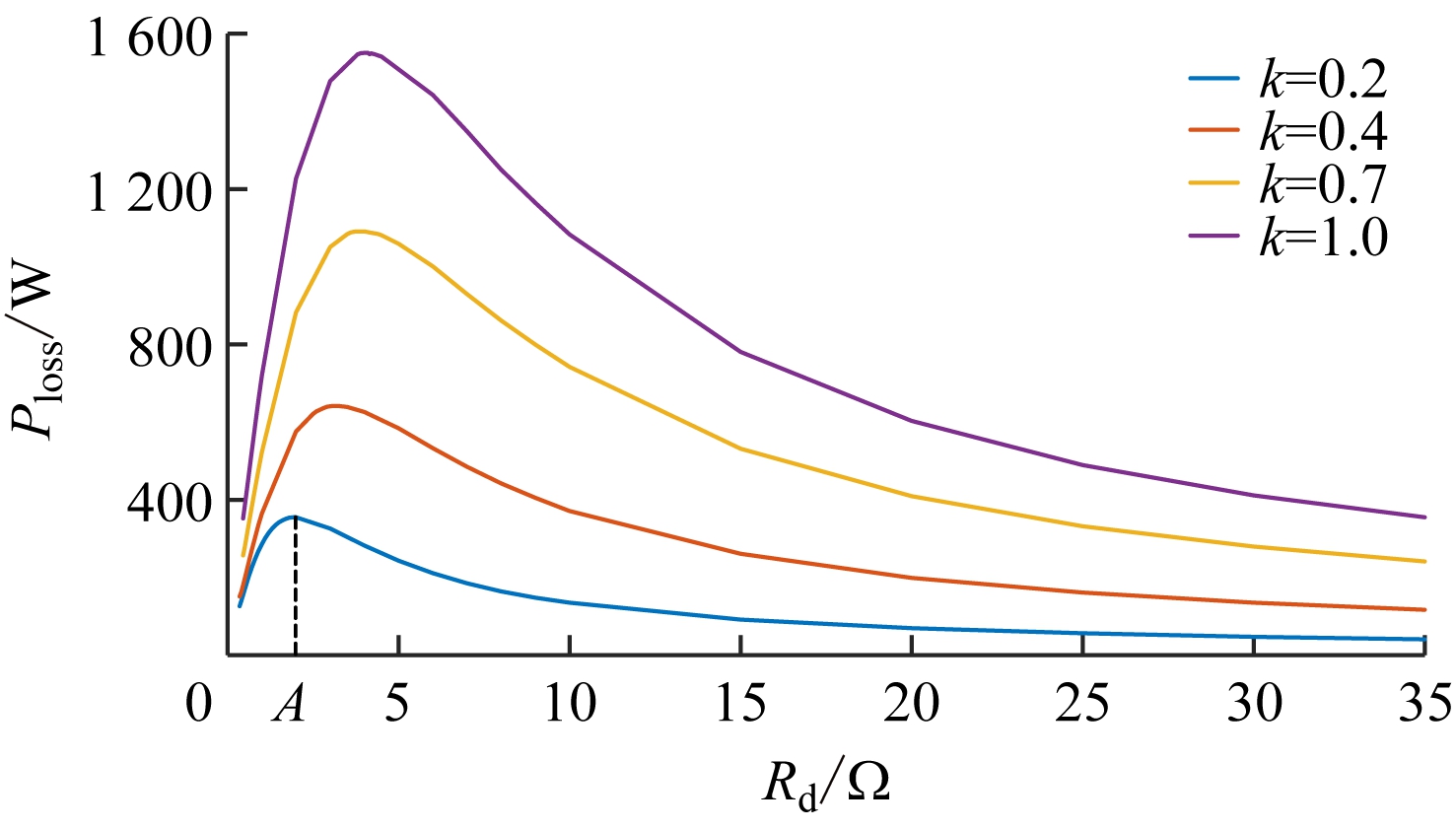
(b)阻尼损耗
图6 电流衰减系数和阻尼损耗关于阻尼电阻的函数曲线
Fig.6 Function curves of current attenuation coefficient and damping loss on damping resistance
为了得到较小的电流衰减系数和较低的阻尼损耗,Rd应在(0,A)范围内选取,且在满足系统一定稳定裕量的要求下尽量小。本文取Rd=0.35 Ω。
4 实验验证
为验证提出的LCL滤波器设计方法的有效性,在Matlab/Simulink中搭建三相电压型PWM整流器控制模型,如图7所示。ud,uq分别为两相旋转坐标系下网侧电压d,q轴分量;id,iq分别为两相旋转坐标系下网侧电流d,q轴分量;![]() 为直流侧给定电压;θ为电网电压旋转角度。采用基于电网电压定向的矢量控制策略。电压电流双闭环控制器均采用PI控制器,PWM调制方式为SVPWM(Space Vector Pulse Width Modulation,空间矢量脉宽调制)。
为直流侧给定电压;θ为电网电压旋转角度。采用基于电网电压定向的矢量控制策略。电压电流双闭环控制器均采用PI控制器,PWM调制方式为SVPWM(Space Vector Pulse Width Modulation,空间矢量脉宽调制)。

图7 三相电压型PWM整流器控制模型
Fig.7 Control model of three-phase voltage type PWM rectifier
仿真参数见表1。
表1 仿真参数
Table 1 Simulation parameters

参数值参数值系统额定功率/kW250额定相电压峰值/V563.4整流器侧滤波电感/mH0.5开关频率/kHz5滤波电容/μF50电流环比例系数1.6阻尼电阻/Ω0.35电流环积分系数166网侧滤波电感/mH0.1电压环比例系数20直流侧稳压电容/μF9000电压环积分系数4250直流侧给定电压/V1200额定负载电阻/Ω5.76
额定负载下直流侧输出电压波形如图8所示,其中t为时间。可看出系统启动时直流侧输出电压超调量很小,约为0.5%,调节时间约为0.04 s,能够快速跟踪给定值并稳定在1 200 V。

图8 直流侧输出电压仿真波形
Fig.8 Simulated waveform of output voltage at DC side
网侧a相电压、电流波形如图9所示。可看出稳态时网侧电流与电压保持同相位,功率因数接近1,且具有很好的正弦化。稳态时网侧a相电流谐波分析结果如图10所示。可看出网侧电流总谐波畸变率(DTH)仅为1.78%,产生的谐波电流很少。

图9 网侧a相电压、电流仿真波形
Fig.9 Simulated waveforms of a-phase voltage and current at power grid side
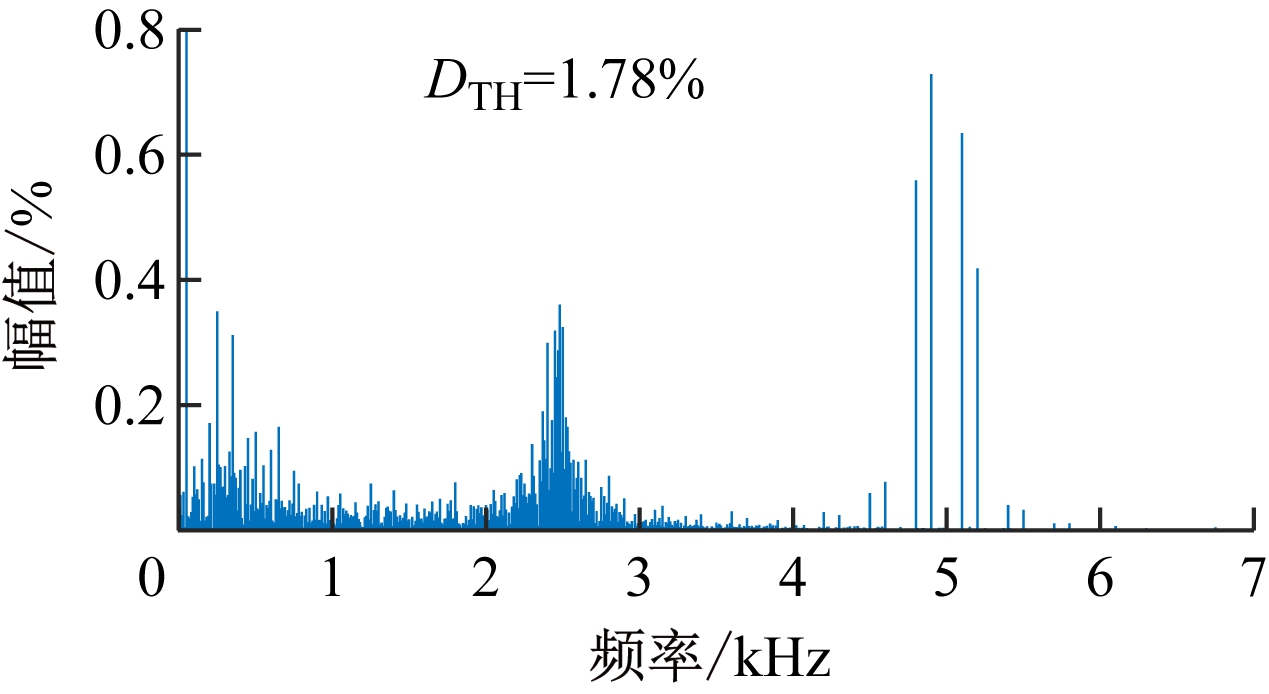
图10 稳态时网侧a相电流谐波分析结果
Fig.10 Harmonic analysis results of a-phase current at power grid side under steady state
采用与仿真模型相同的控制策略和参数,在1台250 kW样机上进行实验验证。样机实物如图11所示。稳态时网侧a相电流波形如图12所示。可看出网侧电流谐波得到较好抑制,并网电流波形质量高。实验与仿真结果较接近。

图11 样机实物
Fig.11 Actual prototype

图12 网侧a相电流实验波形
Fig.12 Experimental waveform of a-phase current at power grid side
在不同功率等级下,对本文方法(设为方法1)与文献[12]中方法(设为方法2)设计的滤波器参数及仿真结果进行对比,结果见表2,其中DTHg为整流器交流侧电流总谐波畸变率。仿真结果均在对应的额定负载情况下得到。
表2 不同功率等级下LCL滤波器设计参数及仿真结果
Table 2 Design parameters and simulation results of LCL filter under different power levels

PN/kW方法L1/mHL2/mHCf/mFRd/ΩDTHg/%Ploss/W5013.000.63103.001.6225.422.500.50101.801.8525.210011.500.32201.501.5950.621.250.25200.901.8450.515011.000.21301.001.6276.320.830.17300.601.8275.920010.750.16400.751.61101.520.620.13400.451.86100.925010.600.13500.601.57125.420.500.10500.351.78125.2
从表2可看出,2种方法设计的滤波器在不同功率等级下的阻尼损耗十分接近,本文方法在整流器交流侧电流总谐波畸变率上略逊于传统方法,但滤波电感和阻尼电阻均明显小于文献[12]方法的设计值,有效降低了成本,减小了整流器体积。
5 结语
提出了一种适用于煤矿井下的PWM整流器LCL滤波器设计方法:在考虑滤波效果、电流快速跟踪能力、系统快速响应能力基础上,为减小整流器体积,应选取较小的总电感;在保证滤波效果前提下,尽量增大滤波电容;在允许的电流总谐波畸变率范围内,尽量选取电感比和阻尼电阻最小值。仿真和实验结果表明,提出的LCL滤波器设计方法能使PWM整流器实现高功率因数和低谐波污染运行,与传统方法相比可明显减小滤波电感和阻尼电阻取值,从而减小整流器体积,降低成本,适用于大中功率刮板输送机、采煤机的变频调速系统。
[1] 李小凡.刮板输送机变频驱动控制系统的研究[D].太原:太原理工大学,2013.
LI Xiaofan.The scraper conveyor variable frequency drive control system[D].Taiyuan:Taiyuan University of Technology,2013.
[2] 卢晓路.采煤机截割部电机变频动态特性分析[D].阜新:辽宁工程技术大学,2015.
LU Xiaolu.Frequency analysis of the dynamic characteristics of the motor shearer cutting unit[D].Fuxin: Liaoning Technical University,2015.
[3] 郑征.双PWM变频器及其协调控制技术研究[D].北京:中国矿业大学(北京),2011.
ZHENG Zheng.The research on dual-PWM converters with power combined control scheme[D].Beijing:China University of Mining and Technology(Beijing),2011.
[4] WESSELS C,DANNEHL J,FUCHS F W.Active damping of LCL-filter resonance based on virtual resistor for PWM rectifiers-stability analysis with different filter parameters[C]//IEEE Power Electronics Specialists Conference,Rhodes,2008:3532-3538.
[5] 刘宝泉,郭华,朱一昕,等.三相变流器无源阻尼型LCL滤波器的分析与设计[J].电工技术学报,2017,32(2):195-205.
LIU Baoquan,GUO Hua,ZHU Yixin,et al.Analysis and design of a passively damping LCL filter in three-phase converters[J].Transactions of China Electrotechnical Society,2017,32(2):195-205.
[6] 曾正,李辉,冉立.交流微电网逆变器控制策略述评[J].电力系统自动化,2016,40(9):142-151.
ZENG Zheng,LI Hui,RAN Li.Conparison on control strategies of inverters in AC microgirds[J].Automation of Electric Power Systems,2016,40(9):142-151.
[7] 黄秋燕,张阁.基于LCL滤波器的电压型PWM整流器的研究[J].工矿自动化,2011,37(3):39-43.
HUANG Qiuyan,ZHANG Ge.Research of voltage source PWM rectifier based on LCL filter[J].Industry and Mine Automation,2011,37(3):39-43.
[8] 刘芳,张喆,马铭遥,等.弱电网条件下基于稳定域和谐波交互的并网逆变器LCL参数设计[J].中国电机工程学报,2019,39(14):4231-4242.
LIU Fang,ZHANG Zhe,MA Mingyao,et al.LCL filter design method based on stability region and harmonic interaction for grid-connected inverters in weak grid[J].Proceedings of the Chinese Society for Electrical Engineering,2019,39(14):4231-4242.
[9] 邓永红,曹浩堃,张全柱.采煤机牵引四象限变流器驱动控制系统设计[J].工矿自动化,2016,42(7):20-25.
DENG Yonghong,CAO Haokun,ZHANG Quanzhu.Design of drive and control system of 4-quadrant converter for traction shearer[J].Industry and Mine Automation,2016,42(7):20-25.
[10] 史丽萍,黄延庆,黄立选.煤矿高功率因数直流牵引供电换流器设计与仿真[J].煤矿机械,2010,31(12):43-45.
SHI Liping,HUANG Yanqing,HUANG Lixuan.Design and simulation of high factor DC converter in coal mine[J].Coal Mine Machinery,2010,31(12): 43-45.
[11] 刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.
LIU Fei,ZHA Xiaoming,DUAN Shanxu.Design and research on parameter of LCL filter in three-phase grid-connected inverter[J].Transactions of China Electrotechnical Society,2010,25(3):110-116.
[12] KARSHENAS H R,SAGHAFI H.Basic criteria in designing LCL filters for grid connected converters[C]//IEEE International Symposium on Industrial Electronics,Montreal,2006:1996-2000.
[13] MARCO L,FREDE B,STEFFAN H.Design and control of an LCL-filter-based three-phase active rectifier[J].IEEE Transactions on Industry Applications,2005,41(5):1281-1291.
