0 引言
滚动轴承是煤矿旋转机械的重要部件,其工作状态直接影响着整机的工作性能。因此,及时对煤矿旋转机械滚动轴承进行状态监测与故障识别,具有重要意义[1]。煤矿旋转机械工作环境恶劣,实际采集到的滚动轴承振动信号受环境噪声干扰明显,且由于传递路径比较复杂,信号呈现出明显的非线性和非平稳性,导致轴承故障特征提取较困难。
多隐层自动编码网络[2]能自动地从滚动轴承振动信号中学习有价值的特征,克服了传统基于“人工特征提取+模式识别”方法受主观影响大的缺陷[3],在滚动轴承故障识别领域取得了较大突破。文献[4]在缺少滚动轴承故障信息的情况下,利用多隐层玻尔兹曼网络取得了较高的识别准确率;文献[5]提出的融合多隐层自动编码网络能更有效、更稳健地对滚动轴承的多种故障进行识别。自动编码网络[6]不需要标记数据,其训练过程为非监督过程,因此,可将自动编码网络的思想应用到极限学习网络[7],得到极限学习自动编码器(Extreme Learning Auto-Encoder,ELAE)。利用ELAE的特征表达能力,将其作为多隐层极限学习自动编码神经网络的基本单元[8]。但ELAE为全连接网络,需要学习的参数众多,训练时间较长,学习到的信号特征的平移不变性较差,受噪声影响较大,且标准ELAE使用sigmoid激活函数,泛化能力较弱[9]。针对上述问题,本文提出一种基于多隐层小波卷积极限学习神经网络(Multi Hidden Layers Wavelet Convolution Extreme Learning Neural Network,MHLWCELNN)的滚动轴承故障识别方法,实验结果表明该方法具有较高的可行性和有效性。
1 多隐层小波卷积极限学习神经网络
1.1 一维卷积神经网络
一维卷积神经网络(1D-CNN)[10]具有局部连接和权值共享特性,可有效降低网络过拟合风险,其工作原理如图1所示。

图1 1D-CNN工作原理
Fig.1 The working principle of 1D-CNN
以卷积层为例,设输入的轴承振动信号为x,则卷积层输出为
Ccn=f(x*Wcn+bcn)
(1)
式中:Ccn为输出特征图;f为激活函数;“*”为卷积符号;Wcn为滤波器权重;bcn为偏置向量。
1.2 自动编码器
1D-CNN为有监督模型,需要大量的带标签样本,而实际工业应用中轴承振动信号无标签样本多。自动编码器(Auto-Encoder,AE)为无监督模型,训练过程只需要无标签样本,AE结构如图2所示,包括输入层、隐层和输出层,其单元个数分别为m,L,m。

图2 AE结构
Fig.2 The structure of AE
AE隐层的输出h为
h=sigmoid(W·x+b)
(2)
式中:W为隐层的权重;b为隐层的偏置。
AE输出层的输出y为
y=sigmoid(W′·h+b′)
(3)
式中:W′为输出层的权重;b′为输出层的偏置。
AE的损失函数E一般为
(4)
式中:S为样本个数;![]() 为第s个样本的第i维输入;
为第s个样本的第i维输入;![]() 为重构输出。
为重构输出。
AE的参数更新策略为
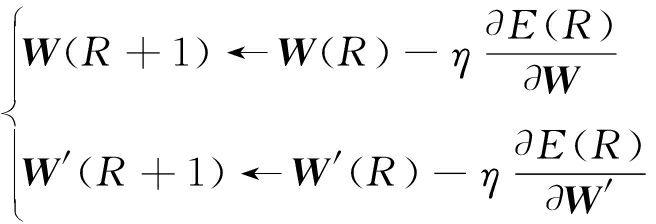
(5)
式中:R为AE训练时的迭代次数;η为AE的学习率。
AE为全连接网络,训练参数较多,且其激活函数为sigmoid函数,泛化能力较弱,另外,AE的参数训练采用BP算法,很容易陷入局部最优。
1.3 小波卷积极限学习神经网络
极限学习机(Extreme Learning Machine,ELM)是一种单隐层神经网络,通过求解矩阵的Moore-Penrose广义逆,进而确定输出权重,训练速度较快。因此,综合1D-CNN,AE,ELM和小波函数的优势,构造小波卷积极限学习神经网络(Wavelet Convolution Extreme Learning Neural Network,WCELNN)。
(1) 将AE和ELM结合,构造ELAE。ELAE为3层无监督网络,其结构与图2类似。ELAE隐层的输出与AE隐层的输出相同,ELAE输出层的输出为
y=hT·β
(6)
式中β为隐层到输出层的输出权重向量。
ELAE的优化函数为
(7)
(8)
式中:I为单位矩阵;A为常数;H为隐层矩阵。
(2) 将ELAE和1D-CNN结合,构造卷积极限学习神经网络(Convolution Extreme Learning Neural Network,CELNN),其结构如图3所示。
CELNN隐层第k个节点的输出hk为
hk=sigmoid(Wk*x+bk)
(9)
式中:Wk为隐层第k个节点的卷积核权重矩阵;bk为隐层第k个节点的偏置。
(3) 将CELNN和小波函数结合,构造WCELNN。由于高斯小波函数在时域、频域均具有良好的分辨率,故激活函数使用高斯小波函数:
(10)
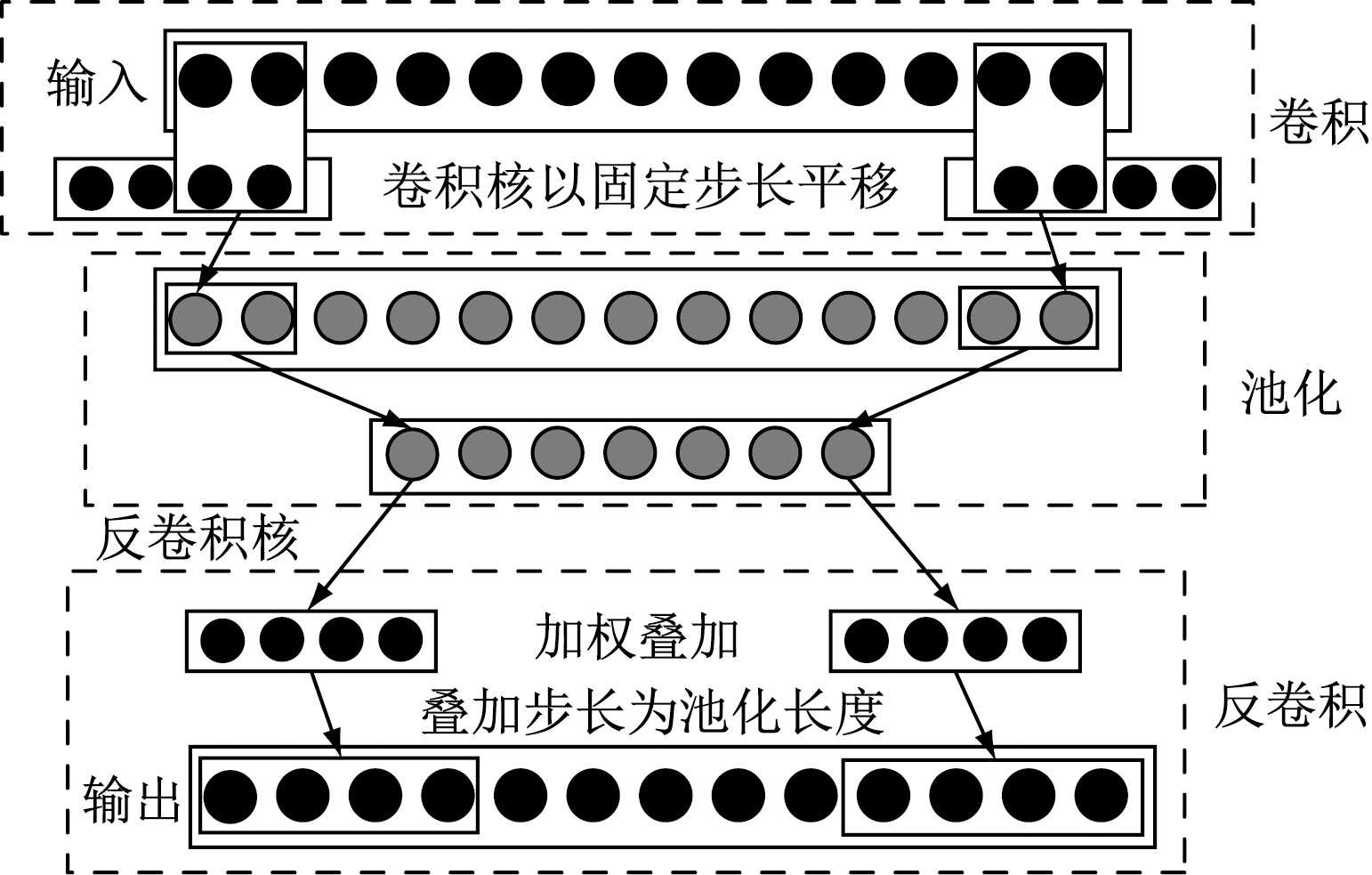
图3 CELNN结构
Fig.3 The structure of CELNN
式中t为时间。
WCELNN隐层第k个节点的输出hk为
hk=ψ[(x*Wk-ck)./ak]
(11)
式中:ak和ck分别为小波节点的尺度向量和平移向量;“./”表示按元素相除。
WCELNN输出层的输出为
(12)
式中![]() 为反卷积核权重矩阵转置。
为反卷积核权重矩阵转置。
根据ELM训练方法,WCELNN的优化函数可表示为
(13)
(14)
WCELNN不使用BP算法,其输出权重计算较为简单,运算速度较快。
2 基于MHLWCELNN的滚动轴承故障识别
MHLWCELNN堆叠多个WCELNN,能进一步提高网络学习到的特征的质量。利用无标签的滚动轴承振动信号样本训练第1层WCELNN,得到第1隐层特征;将第1隐层特征输入第2层WCELNN,得到第2隐层特征;依此类推。MHLWCELNN结构如图4所示。
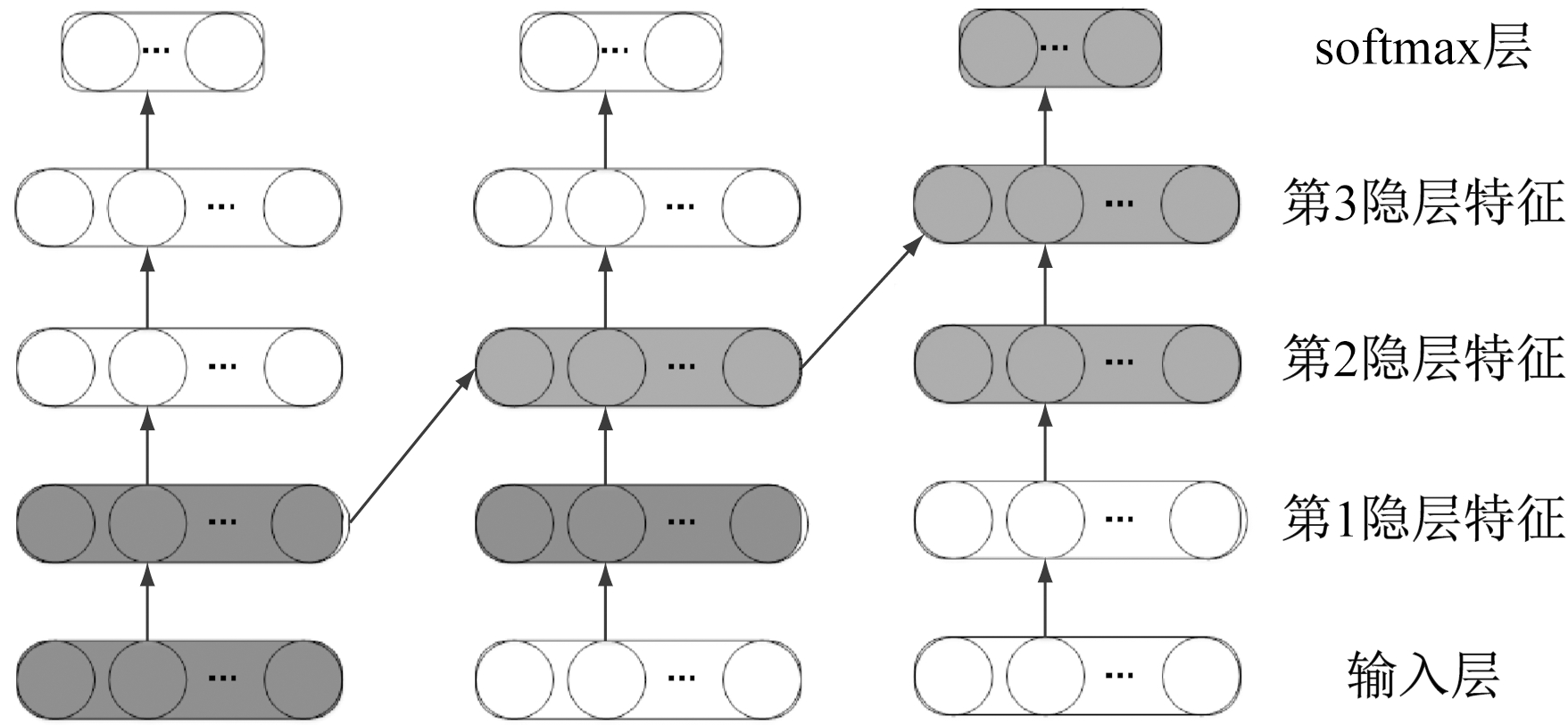
图4 MHLWCELNN结构
Fig.4 The structure of MHLWCELNN
基于MHLWCELNN滚动轴承故障识别步骤如下:① 采集不同工况下的滚动轴承振动信号并进行样本划分。② 将训练样本输入MHLWCELNN进行训练。③ 使用测试样本对训练好的网络进行测试。
3 实验验证:基于XJTU-SY数据集
3.1 实验数据描述
为验证MHLWCELNN的有效性,以XJTU-SY滚动轴承数据集[11]为对象进行实验。实验轴承为LDK UER204滚动轴承。限于计算资源,在XJTU-SY数据集中选取9种不同的轴承工况数据:正常(a,b)、内圈轻微故障(c)、内圈中度故障(d)、内圈重度故障(e)、外圈轻微故障(f)、外圈中度故障(g)、外圈重度故障(h)、滚珠轻微故障(i)、滚珠中度故障(j),最后得到每种工况下的8 000个样本,随机选取70%作为训练样本,其余作为测试样本,每个样本1 024个采样点,即1 024维。
各种工况下的轴承时域信号如图5所示,可见振动信号受噪声干扰严重,难以进行有效区分。
(a) 工况a

(b) 工况b

(c) 工况c

(d) 工况d
(e) 工况e
(f) 工况f

(g) 工况g
(h) 工况h
(i) 工况i
(j) 工况j
图5 各种工况下的轴承时域信号
Fig.5 Bearing time domain signal under
various working conditions
3.2 故障识别与分析
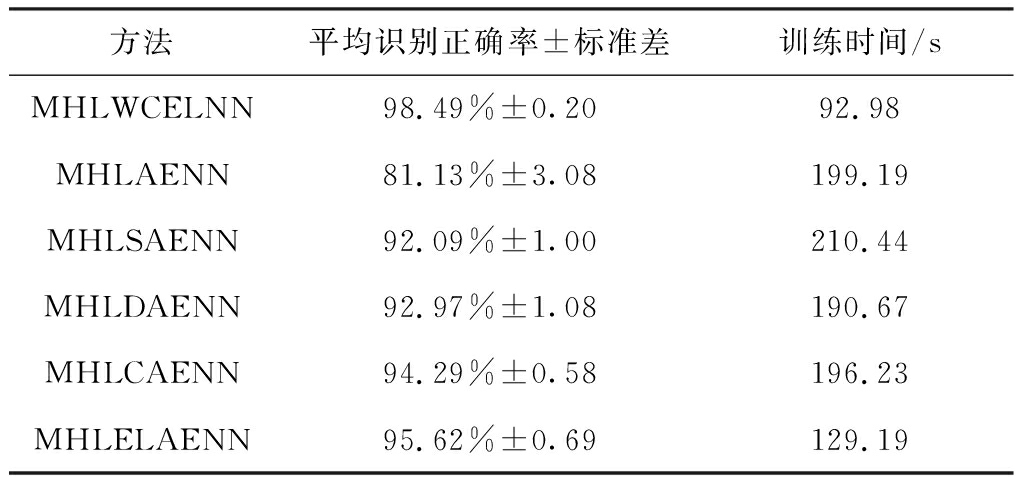
为验证MHLWCELNN的优势,采用多隐层自动编码神经网络(Multi Hidden Layers Auto Encoder Neural Network,MHLAENN)、多隐层稀疏自动编码神经网络[12](Multi Hidden Layers Sparse Auto Encoder Neural Network,MHLSAENN)、多隐层降噪自动编码神经网络[13](Multi Hidden Layers Denoising Auto Encoder Neural Network,MHLDAENN)、多隐层收缩自动编码神经网络[14](Multi Hidden Layers Contractive Auto Encoder Neural Network,MHLCAENN)和多隐层极限学习自动编码神经网络(Multi Hidden Layers Extreme Learning Auto Encoder Neural Network,MHLELAENN)等方法进行对比分析,输入均为1 024维信号样本,各网络结构均为1 024-512-256-128-64-32-10。共进行10次试验,不同方法的识别结果见表1。
表1 不同方法的识别结果(基于XJTU-SY数据集)
Table 1 Identification results of different methods
(based on XJTU-SY data set)
方法平均识别正确率±标准差训练时间/sMHLWCELNN98.49%±0.2092.98MHLAENN81.13%±3.08199.19MHLSAENN92.09%±1.00210.44MHLDAENN92.97%±1.08190.67MHLCAENN94.29%±0.58196.23MHLELAENN95.62%±0.69129.19
由表2可知,MHLWCELNN具有更高的识别准确率和更小的标准差,能较为稳定地识别出滚动轴承的故障类型。这几种方法中,MHLAENN方法的故障识别率最低,仅81.13%;MHLSAENN加入了稀疏项限制,可捕捉输入数据中较重要的信息;MHLDAENN加入了降噪机制,一定程度上提高了网络对噪声的鲁棒性;MHLCAENN加入了收缩项限制,使网络对输入信号的小扰动具有一定的抗干扰性。MHLSAENN,MHLDAENN和MHLCAENN较MHLAENN都取得了更高的故障识别率。MHLELAENN 利用ELAE优秀的特征表达能力和快速的网络收敛能力,故障识别率达到了95.62%,训练时间仅129.19 s。本文提出的MHLWCELNN采用局部连接和权值共享机制,大大减少了需要学习的参数,故训练时间较短,受噪声影响较小,且使用小波激活函数,具备一定的时频聚焦特性,能有效学习轴承振动信号的时频特征,故障识别率高于其他方法。
3.3 基于不平衡数据集的故障识别率
为验证MHLWCELNN对不平衡故障样本的有效性,设计了一种不平衡数据集,正常与故障工况的训练样本比例为8 000∶4 000,实验共进行10次,采用MHLCAENN,MHLELAENN方法作为对比。
准确率、召回率、F1值作为评估指标,经常被用到分类效果的评测上。其中F1值可在准确率和召回率之间取得平衡,让两者同时达到最高。因此,采用F1值定量评价3种方法基于不平衡数据集的分类效果,F1值计算公式为
(15)
式中:F1值在[0,1]之间,0代表最差,1代表最好;P为准确率;Q为召回率。
不同方法的F1值见表2。
表2 不同方法的F1值
Table 2 F1 values of different methods

工况F1值MHLWCELNNMHLCAENNMHLELAENNa0.9520.9230.921b0.9530.9110.909c0.9610.9290.918d0.9600.9190.913e0.9590.9210.919f0.9410.9110.920g0.9460.9010.913h0.9600.9090.915i0.9590.8810.908j0.9420.9110.891
由表2可知,MHLWCELNN的F1值较高,验证了MHLWCELNN对不平衡数据集的有效性。
3.4 激活函数对MHLWCELNN识别率的影响
激活函数对MHLWCELNN的故障识别率有一定影响,采用不同激活函数时MHLWCELNN的识别率见表3。从表3可知,高斯小波、Morlet小波和Mexican hat小波的故障识别效果好于其他激活函数,高斯小波在时域、频域均有较高的分辨率。
表3 不同激活函数对MHLWCELNN识别率的影响
Table 3 Effects of different activation functions on
identification accuracy of MHLWCELNN

激活函数识别率/%激活函数识别率/%ReLU95.14GELU95.42LReLU95.82Swish95.17ELU94.64Morlet小波97.72sigmoid90.47Mexican hat 小波98.01高斯小波98.49
4 实验验证:基于西储大学数据集
4.1 实验数据描述
以西储大学轴承数据集为对象,在测试轴承上通过电火花加工形成不同故障尺度的凹坑,限于计算资源,从西储大学轴承数据集中选取7种不同的轴承故障工况数据:正常(A)、内圈轻微故障(B)、内圈中度故障(C)、外圈轻微故障(D)、外圈中度故障(E)、滚动体轻微故障(F)、滚动体中度故障(G),每种工况的样本数量为8 000。7种轴承故障工况下的时域信号及相应的频域信号如图6所示。从图6可知,故障信号受噪声干扰严重,难以直接从时域图中对滚动轴承的故障类型及程度进行有效区分。

(a) 工况A,时域信号

(b) 工况A,频域信号
(c) 工况B,时域信号

(d) 工况B,频域信号
(e) 工况C,时域信号

(f) 工况C,频域信号
(g) 工况D,时域信号

(h) 工况D,频域信号
(i) 工况E,时域信号

(j) 工况E,频域信号

(k) 工况F,时域信号

(l) 工况F,频域信号

(m) 工况G,时域信号

(n) 工况G,频域信号
图6 滚动轴承各种工况下的的时域和频域信号
Fig.6 Time domain and frequency domain signals of
rolling bearings under various working conditions
4.2 故障识别与分析
采用MHLWCELNN等6种方法进行对比实验,结果见表4。
从表4可知,MHLWCELNN具有更高的识别准确率和更小的标准差,能较为稳定地识别出滚动轴承的不同故障类型,进一步验证了MHLWCELNN的优越性。
表4 不同方法的识别结果(基于西储大学数据集)
Table 4 Identification results of different methods
(based on the data set of Western Reserve University)

方法识别正确率±标准差用时/sMHLWCELNN98.35%±0.3183.47MHLAENN85.87%±2.16178.48MHLSAENN91.73%±1.57185.27MHLDAENN93.58%±1.31180.90MHLCAENN94.73%±1.06188.61MHLELAENN95.98%±0.57191.89
4.3 训练集占比对故障识别准确率的影响
训练集和测试集的样本比例对MHLWCELNN的轴承故障识别准确率有一定影响。若训练集样本比例过低,会引起MHLWCELNN欠拟合;若训练集样本比例过高,则会引起MHLWCELNN过拟合。欠拟合和过拟合均会影响网络的识别准确率。训练集样本占比为60%~90%时,MHLWCELNN的故障识别率如图7所示。

图7 训练集样本占比对故障识别准确率的影响
Fig.7 Effect of proportions of training set on
fault identification accuracy
从图7可知,训练集样本占比为60%~80%时, MHLWCELNN的故障识别率随训练集样本所占比例增加而增加;当训练集样本占比超过80%时,故障识别率不再上升,故设置训练集样本占比为80%较合适。
5 结论
提出了一种基于MHLWCENN的滚动轴承故障识别方法,该方法学习能力和泛化能力强,且具有局部连接特性和权值共享特性,更适用于非线性和非平稳性轴承振动信号。基于XJTU-SY数据集和西储大学数据集的实验结果表明:
(1) 与MHLAENN,MHLSAENN等相比,MHLWCELNN能有效学习轴承振动信号的时频特征,具有更高的识别准确率和更小的标准差。
(2) MHLWCELNN的F1值高于MHLCAENN,MHLELAENN,验证了MHLWCELNN对不平衡数据集的有效性。
(3) 高斯小波、Morlet小波和Mexican hat小波的故障识别效果好于其他激活函数,高斯小波在时域、频域均有较高的分辨率。
(4) MHLWCELNN的故障识别率随训练集样本所占比例增加而增加,当训练集样本占比超过80%时,故障识别率不再上升,故设置训练集样本占比为80%较合适。
[1] 鞠晨,张超,樊红卫,等.基于小波包分解和PSO-BPNN的滚动轴承故障诊断[J].工矿自动化,2020,46(8):70-74.
JU Chen,ZHANG Chao,FAN Hongwei,et al.Rolling bearing fault diagnosis based on wavelet packet decomposition and PSO-BPNN[J].Industry and Mine Automation,2020,46(8):70-74.
[2] SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks,2015, 61(1):85-117.
[3] SHAO Haidong, JIANG Hongkai, LI Xingqiu, et al. Intelligent fault diagnosis of rolling bearing using deep wavelet auto-encoder with extreme learning machine[J]. Knowledge-Based Systems, 2018,140: 1-14.
[4] SHAO Haidong, JIANG Hongkai,ZHANG Xun, et al. Rolling bearing fault diagnosis using an optimization deep belief network[J].Measurement Science & Technology,2015,26(11):115002-115018.
[5] SHAO Haidong, JIANG Hongkai,WANG Fu'an, et al. An enhancement deep feature fusion method for rotating machinery fault diagnosis[J]. Knowledge-Based Systems, 2017,119:200-220.
[6] SHIN H C, ORTON M R, COLLINS D J, et al. Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(8):1930-1943.
[7] 杨超,杨晓霞,李灵飞.基于灰色关联度和ELM的轴承性能退化趋势预测[J].组合机床与自动化加工技术,2019(11):105-108.
YANG Chao,YANG Xiaoxia,LI Lingfei.Prediction of bearing performance degradation trend based on grey relational degree and ELM[J].Modular Machine Tool & Automatic Manufacturing Technique,2019(11):105-108.
[8] 边冰,赵明政.基于深度极限学习机的水质预测研究[J].华北理工大学学报(自然科学版),2020,42(1):51-57.
BIAN Bing,ZHAO Mingzheng.Study on water quality prediction based on deep extreme learning machine[J].Journal of North China University of Science and Technology(Natural Science Edition), 2020,42(1):51-57.
[9] 邹剑晖,敖银辉.基于CEEMD和小波核极限学习机的轴承故障诊断[J].组合机床与自动化加工技术,2019(11):74-77.
ZOU Jianhui,AO Yinhui.Bearing fault diagnosis based on CEEMD and wavelet kernel extreme learning machine[J].Modular Machine Tool & Automatic Manufacturing Technique,2019(11):74-77.
[10] 林景栋,吴欣怡,柴毅,等.卷积神经网络结构优化综述[J].自动化学报,2020,46(1):24-37.
LIN Jingdong,WU Xinyi,CHAI Yi,et al.Structure optimization of convolutional neural networks: a survey[J].Acta Automatica Sinica,2020,46(1):24-37.
[11] 雷亚国,韩天宇,王彪,等.XJTU-SY滚动轴承加速寿命试验数据集解读[J].机械工程学报,2019, 55(16):1-6.
LEI Yaguo,HAN Tianyu,WANG Biao,et al. XJTU-SY rolling element bearing accelerated life test datasets: a tutorial[J].Journal of Mechanical Engineering,2019,55(16):1-6.
[12] ZHENG Ling,YAN Panfei,CHEN Fei. Power grid fault diagnosis method based on stacked sparse denoising auto-encoder and GRU network[J]. Journal of Physics: Conference Series,2020, 1631:012114.
[13] LU Chen,WANG Zhenya,QIN Weili, et al. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification[J]. Signal Processing, 2017,130: 377-388.
[14] XU Jun,XIANG Lei,LIU Qingshan, et al. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images[J]. IEEE Transactions on Medical Imaging,2016,35(1): 119-130.
