0 引言
瞬变电磁法是指利用发射线圈向地下发射一次脉冲磁场,通过接收线圈接收地下的感应电流产生的二次场,从而探测介质电阻率的一种方法。瞬变电磁法具有施工效率高、对低阻体敏感等优点,适用于井下掘进巷道及回采工作面顶底板含水性探测、掘进巷道超前探测及隧道地质构造富水性探测等。
在电磁学中,正演是指将已知的电荷属性换算成电场分布,并计算得到空间某点的电场属性;反演是指通过电场分布得到一种电荷分布模型或近似模型,得到实际地层的地电特性。通过一维反演只能得到深度信息,而通过二维反演则可以得到横向和纵向地电特性,对异常区的圈定由1个方向变为2个方向,从而提高探测精度。煤矿井下瞬变电磁的探测范围是全空间的,在全空间瞬变电磁法数据处理过程中很少加入反演计算,常用的线性反演难以满足生产需求[1-2]。然而,非线性反演问题复杂,现有研究多停留在一维反演阶段,很少涉及二维非线性反演。为了满足生产需求,提高反演精度,有必要研究二维非线性反演方法。在通过全空间瞬变电磁法采集的原始数据处理过程中加入二维反演计算,对提高探测精度和分辨率具有重要意义。
粒子群算法是一种非线性反演计算方法,在反演过程中可以适应地电特性的变化,因此,学者们将其应用到瞬变电磁反演计算中并进行了改进研究。文献[3-4]对全空间瞬变电磁法进行了粒子群优化反演研究,改进了粒子群寻优算法,但只进行了一维反演计算,未解决体积效应问题。文献[5]主要从算法方面对粒子群反演方法进行改进,未结合实际应用数据进行分析验证。文献[6]最早将一维非线性反演技术引入到地球物理探测中,开拓了粒子群反演的先河,但是寻优算法还有待改进。文献[7-8]对地球物理反演基础理论进行了研究,但在全空间瞬变电磁方面未进行理论研究和实际应用。文献[9-10]引入粒子群算法并进行了系统研究,为全空间瞬变电磁反演计算研究提供了基础。
随着煤矿开采深度的加大,水害威胁越来越严重,针对煤矿实际采掘情况的复杂性,为了提高探测精度,为钻探提供有效靶点,有必要开展全空间瞬变电磁二维反演方法的研究,为矿井水害防治提供可靠的地质资料。本文在一维反演和二维正演研究的基础上,结合煤矿实际探测精度要求,提出了基于粒子群的全空间瞬变电磁二维反演方法,通过粒子群算法对电阻率和地层厚度参数进行寻优,以提高反演精度,为全空间瞬变电磁资料处理解释奠定基础。
1 全空间瞬变电磁二维反演方法
在全空间的前提下,二维反演和一维反演都是根据瞬变电磁仪探测到的归一化感应电位值和与之对应的时间进行反演计算,最终得到探测目标体的电性参数。由于实际地层的电性结构是复杂的三维结构,仅仅依靠一维反演结果来反映地层的地电特性误差可能较大,需通过二维反演来反映地层的真实情况。
基于粒子群的全空间瞬变电磁二维反演方法流程如图1所示。
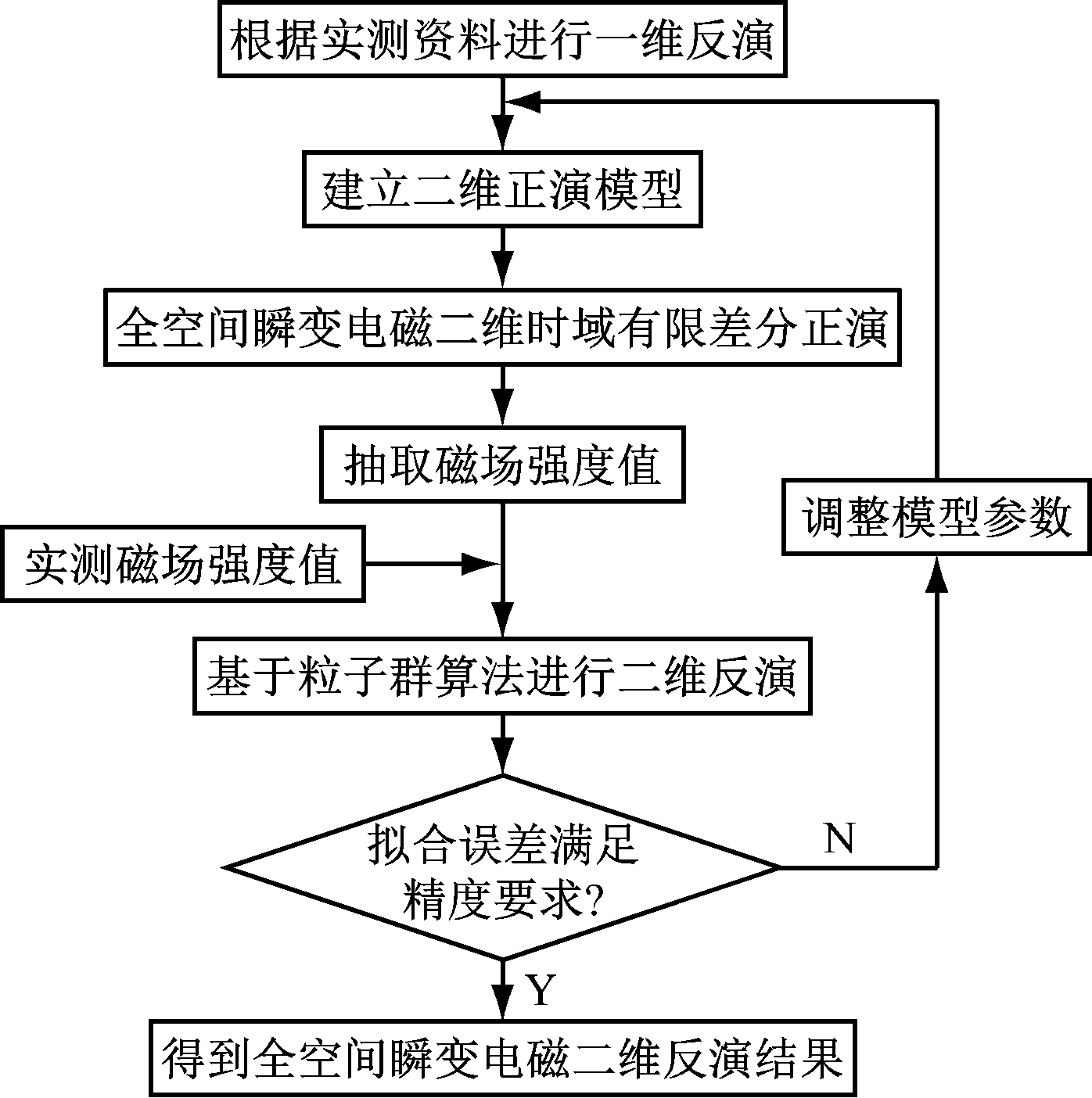
图1 基于粒子群的全空间瞬变电磁二维反演方法流程
Fig.1 Flow of two-dimensional inversion method of
transient electromagnetic in whole-space
based on particle swarm
具体步骤如下:
(1) 基于实测资料,通过粒子群算法进行全空间瞬变电磁一维反演。以一维反演结果中的探测深度值及其对应的视电阻率值作为初始模型参数,建立二维正演模型。
(2) 选用等间距分布的网格对二维正演模型进行网格化,每个网格的大小为1 m×1 m。对网格化的二维正演模型进行时域有限差分模拟,得到不同时刻各网格节点处的磁场强度值。
(3) 按照原始数据采集时的时间门所对应的时间和一维反演结果中的探测深度来抽取正演模拟后的磁场强度值,使得抽取的磁场强度值与实测资料中的磁场强度值具有时间和深度的对应关系。
(4) 基于最小二乘反演计算方法,对抽取的磁场强度值与实测资料中的磁场强度值进行反演计算。通过调整二维正演模型中的地电参数,使得最小二乘反演后的拟合误差处在适合二维反演的误差区间。
(5) 对经过最小二乘法反演后得到的磁场强度值和与之对应的时间值按测点号顺序依次进行二维反演[11-13]。
已知n个时间门的全空间瞬变电磁响应bw(w=1,2,…,n),模型M(q)(q=1,2,…,2K-2)包括K层地层的电阻率和K-2层地层的厚度参数,需要求得模型M(q)的响应mw,使其与已知的电磁响应bw一致,即满足方程bw=mw,也就是求fw=bw-mw=0的解。由最小二乘法理论可知,只需求F=![]() 的极小值即可。因为方程是非线性的,直接求其极小值较困难,所以采用迭代的方法来求解。
的极小值即可。因为方程是非线性的,直接求其极小值较困难,所以采用迭代的方法来求解。
模型M(q)的参数包括K层地层的电阻率和K-2层地层的厚度,给定参数初始值x0,即一维反演得到的视电阻率和与之对应的探测深度,令迭代过程中模型参数的修正方程为[10-11,13]
AT(f(x0)+AΔx0)=0
(1)
式中:A为雅克比距阵;f(x0)为函数F泰勒展开的一阶项;Δx0为迭代过程中模型参数的修正值。
由式(1)可求得模型参数修正值为
Δx0=-(ATA)-1ATf(x0)
(2)
模型的近似解为x1=x0+Δx0,将x1作为下次迭代的初始值,进行多次迭代,直至拟合误差满足精度要求为止。
反演过程中模型参数修正对反演效果起着至关重要的作用。给定一组参数,可得到一个对应的模型参数修正值,通过参数调整,可得到若干模型参数修正值。将各模型参数修正值作为迭代的初始值,经过多次迭代后,若结果拟合误差符合精度要求,则停止迭代,该结果为最终的反演结果;若拟合误差不满足精度要求,则继续迭代或更换模型参数修正值后继续迭代,直到拟合误差满足精度要求为止[11]。
2 基于粒子群算法的参数寻优
粒子群的寻优过程其实就是群体中所有粒子聚拢向最优位置的过程。为了分析粒子群算法在全空间瞬变电磁反演中的寻优能力,从定量分析的角度分析该算法的基本原理。开始寻优时,在搜索区域中初始化若干个粒子,以这些粒子的参数作为迭代的初始值,根据需求来定义第i个粒子的初始位置![]() 和速度
和速度![]() (j为粒子搜索的空间维度,k为当前迭代次数)。速度和位置的更新公式为[1,11-12]
(j为粒子搜索的空间维度,k为当前迭代次数)。速度和位置的更新公式为[1,11-12]
![]()
![]()
(3)
(4)
式中:χ为收缩因子,![]() 学习因子,一般取c1=c2=2.05,则χ=0.729 84;ω为惯性因子,
学习因子,一般取c1=c2=2.05,则χ=0.729 84;ω为惯性因子,![]() 的随机数;gbest为粒子的历史最优位置;pbest为粒子当前的最优位置。
的随机数;gbest为粒子的历史最优位置;pbest为粒子当前的最优位置。
3 模型非线性反演
3.1 模型瞬变电磁响应规律分析
以煤矿井下(含巷道)全空间水平层状地层为基础建立典型的3层模型,进行二维反演模拟,验证反演算法的准确性,从而为实际资料的反演提供参考。Q型地电模型如图2所示,l轴表示模型长度,z轴表示模型宽度。

图2 Q型地电模型
Fig.2 Q-type geoelectric model
模型共分为3层:第1层是顶板砂岩层,设电阻率ρ1为500 Ω·m,层厚h1为80 m;第2层是煤层,设电阻率ρ2为400 Ω·m,层厚h2为20 m,巷道位于该层最下端,发射线框和接收线框以重叠回线的方式水平放置于巷道中央;第3层是底板灰岩层,设电阻率ρ3为200 Ω·m,层厚h3为100 m[14-16]。模型的长度和宽度都设置为200 m,网格剖分时1个单位代表1 m。
激发源位于l=100 m,z=0处,通过发射线框发射一次脉冲磁场,并分析磁场在模型地层中的传播规律[15-17]。时间步长为800,1 600时Q型地电模型瞬变电磁场扩散切片如图3所示,其中y为与层状地层走向垂直方向距巷道顶板的距离,在巷道顶板处y=0。从图3可看出,自y=0断面向y=80 m断面,磁场强度值及扩散范围均逐渐变小;z>100 m范围内的磁场扩散速率大于z<100 m范围内的磁场扩散速率,反映了z>100 m范围内的电阻率高于z<100 m范围内的电阻率,与地层模型中设置的电阻率相对应。综合分析可知,随着时间的增加,磁场扩散范围明显增大;因为磁场在扩散过程中不断衰减,所以靠近激发源处磁场强度值较大,远离激发源处磁场强度值较小。
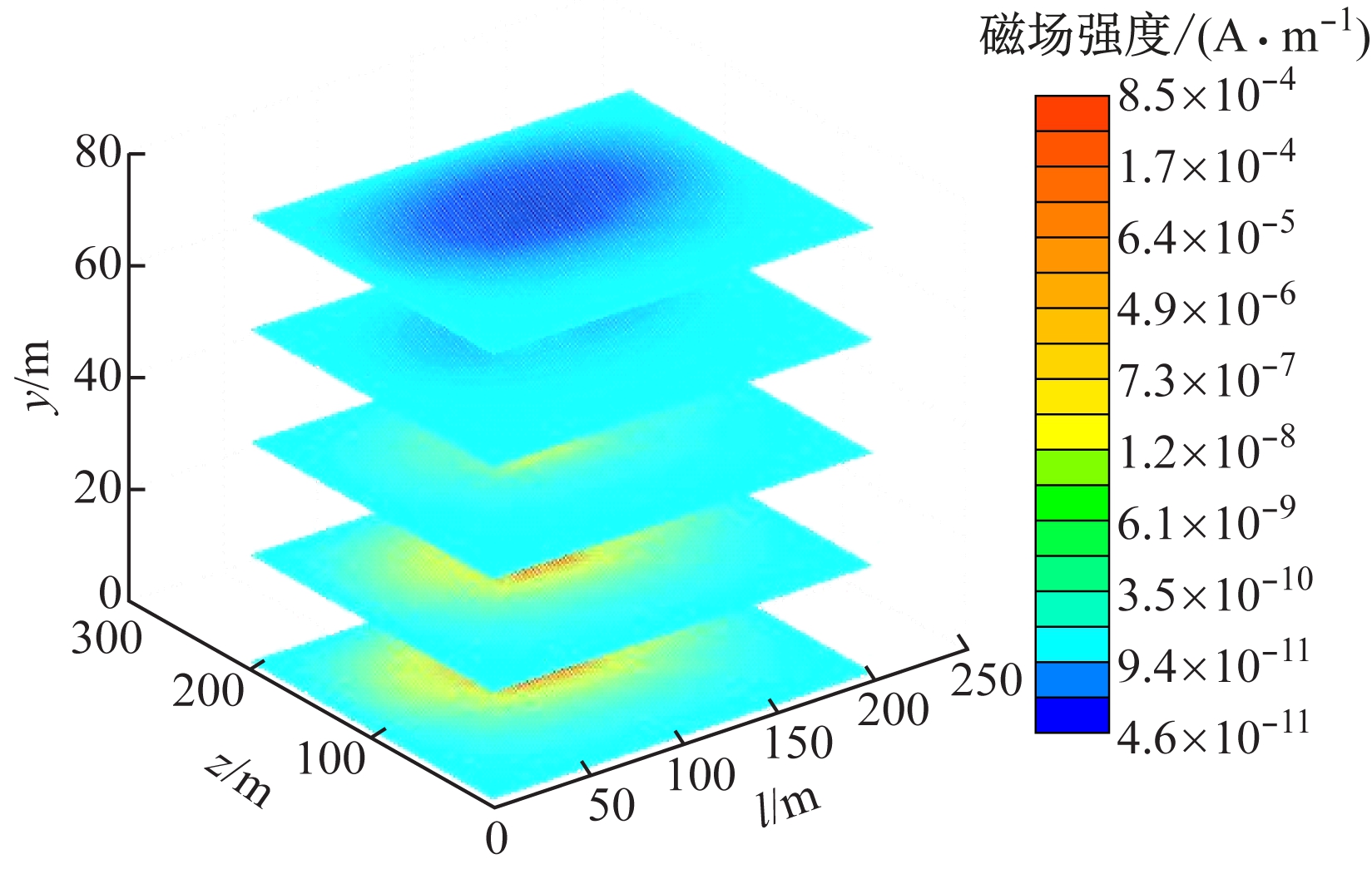
(a) 时间步长为800
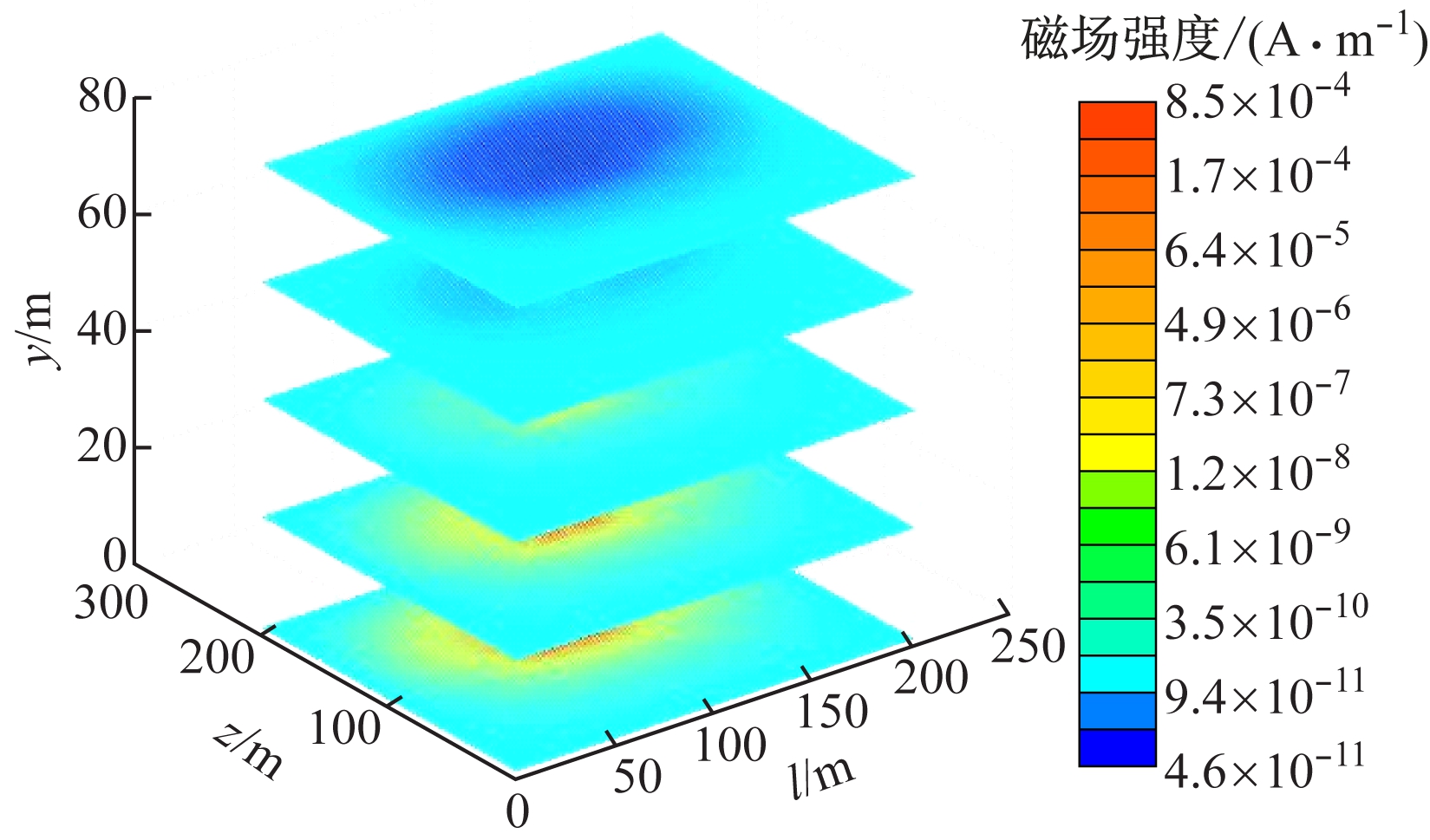
(b) 时间步长为1 600
图3 Q型地电模型瞬变电磁场扩散切片
Fig.3 Transient electromagnetic field diffusion slice
of Q-type geoelectric model
3.2 模型粒子群反演误差分析
Q型地电模型瞬变电磁反演计算拟合误差如图4所示。迭代2次时拟合误差为1×10-2,迭代10次时拟合误差为1×10-3,迭代50次时拟合误差为1.3×10-4。对于前20次迭代,随着迭代次数的增大,拟合误差下降速率较大;对于第21次到第50次迭代,随着迭代次数的增大,拟合误差下降速率明显减小,整体反演精度相对较高。
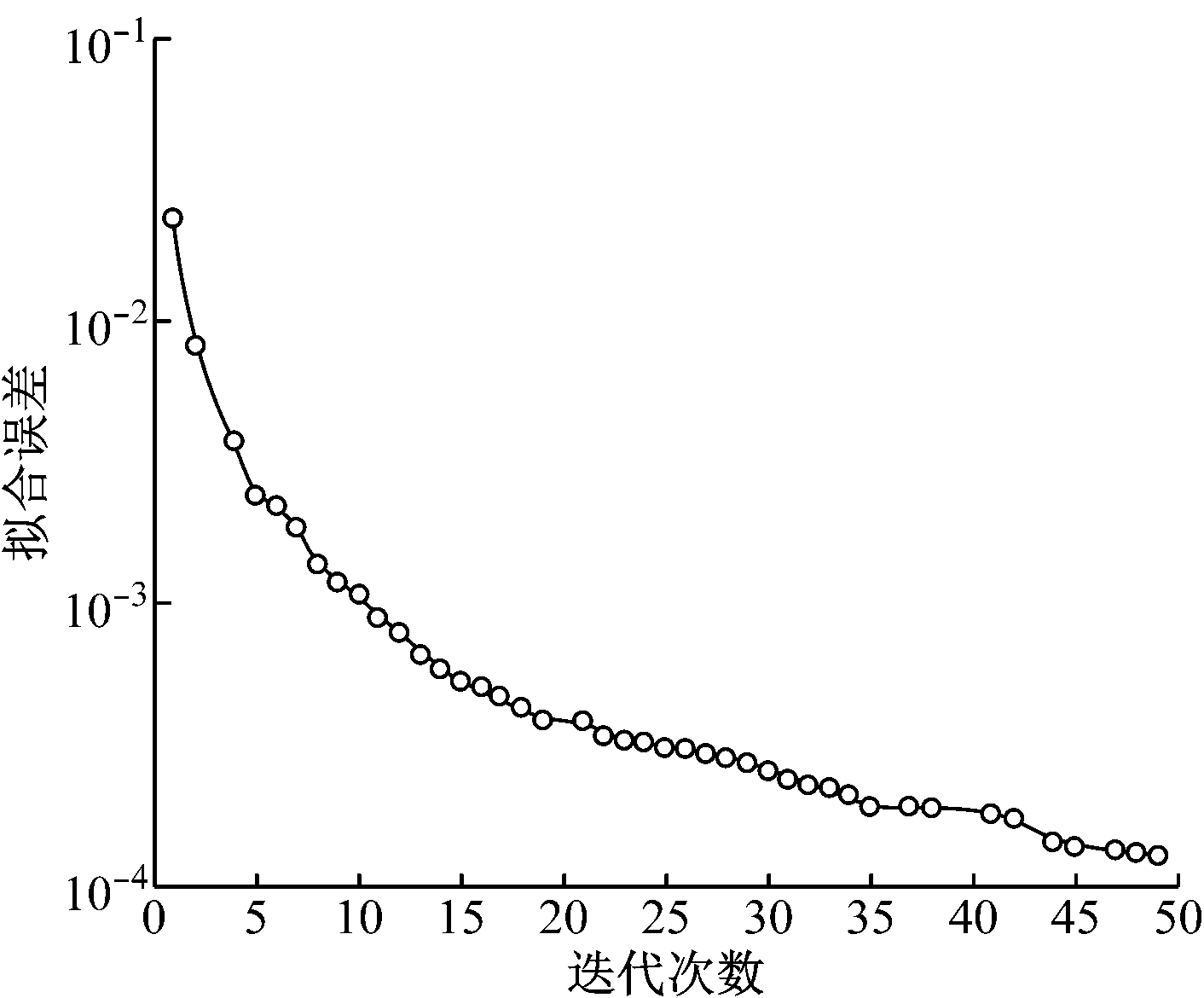
图4 Q型地电模型瞬变电磁反演计算拟合误差
Fig.4 Fitting error of transient electromagnetic inversion
calculation of Q-type geoelectric model
4 工程应用
选取某矿-550 m水平西翼总回巷道底板瞬变电磁探测资料进行反演计算,由巷道东段向西段依次采集数据,探测起点定为0号测点,测点间距为10 m,探测终点为200号测点,测点总数为21个,总探测长度为200 m[11]。
4.1 瞬变电磁场扩散规律
时间步长为2 500时的瞬变电磁场扩散图如图5所示,激发源位于l=100 m,z=0处,z轴坐标值的负号表示底板以下探测深度,正号表示巷道顶板以上探测深度;l轴坐标值与实测数据的测点号相对应,例如,l=10 m时,对应的测点号为10号。
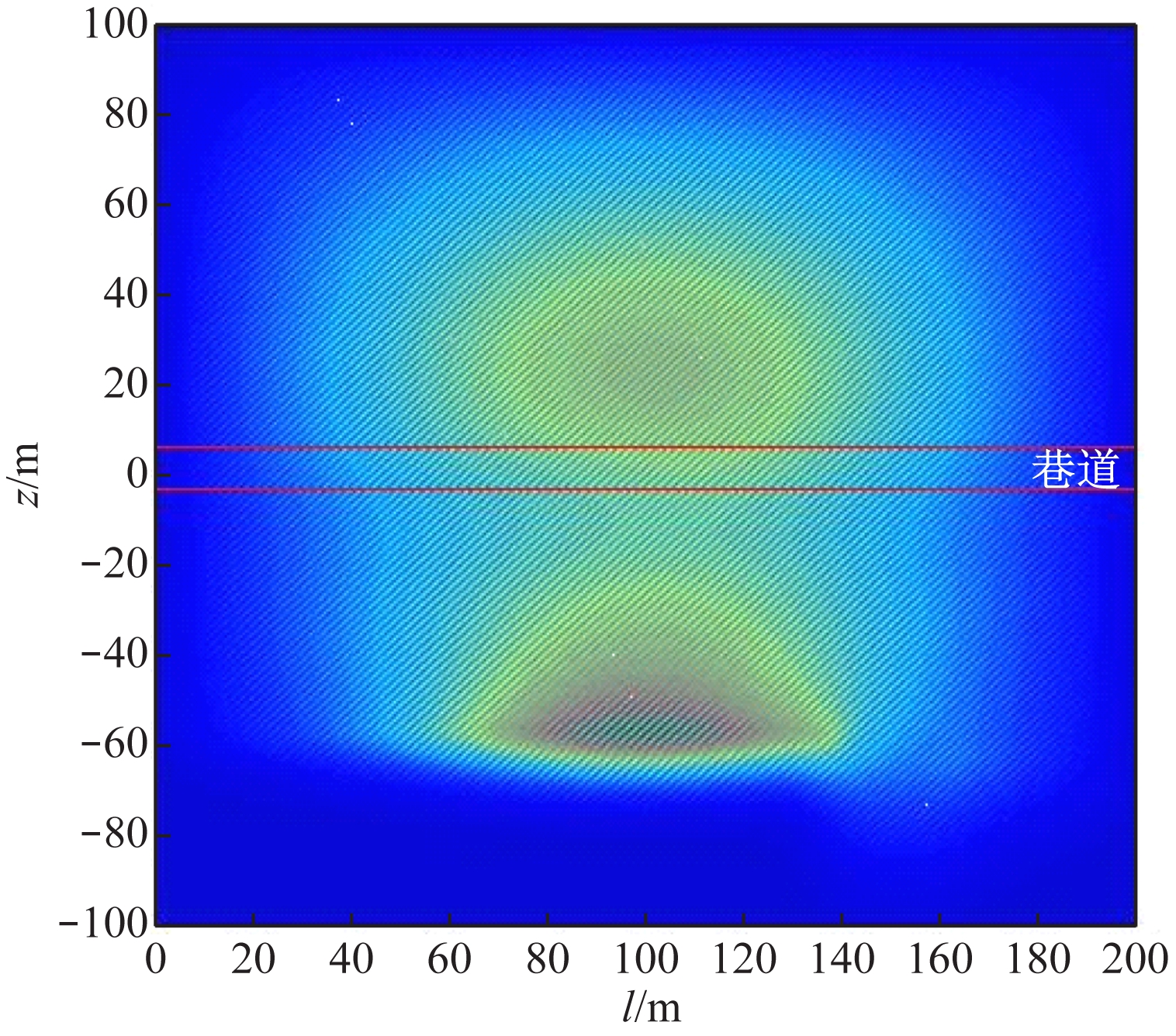
图5 时间步长为2 500时的瞬变电磁场扩散图
Fig.5 Transient electromagnetic field diffusion diagram
when the time step is 2 500
从图5可看出,由于存在巷道空间,瞬变电磁场扩散到巷道边界时发生畸变,随着时间的推移,巷道边界对瞬变电磁场扩散造成的影响逐渐减弱,瞬变电磁场开始向巷道顶板以上地层和底板以下地层扩散。因为巷道顶板以上地层没有异常体,磁场均匀扩散,所以瞬变电磁场强度逐渐减弱。底板以下地层中存在低阻异常体,瞬变电磁场在低阻体中扩散速度较慢,因此,瞬变电磁场在低阻异常体边界处形成新的激发扩散源。
根据图5可确定低阻异常体的边界,只是140号测点到200号测点探测深度为底板以下65~100 m时,低阻体处于模型的右下角,此时该区域瞬变电磁场强度较弱,使得低阻异常体的边界不是很明显。
4.2 反演误差分析
磁场强度拟合误差曲线如图6所示。在前11次迭代过程中,随着迭代次数增加,拟合误差迅速下降;到第11次迭代时,拟合误差为0.8%,小于拟合误差精度要求,拟合效果较好;之后,随着迭代次数的增加,拟合误差下降趋势不明显,曲线逐渐趋于平缓;到第30次迭代时,拟合误差仅为0.44%。当迭代次数增大到一定程度时,如果继续增大迭代次数,则拟合误差减小幅度很小,但是反演计算所用时间会成倍增加,反而会降低计算效率。因此,在反演过程中需要选取合适的迭代次数,使得反演后的拟合误差满足精度要求。本次反演计算所用时间为76.592 232 s,计算效率较高。
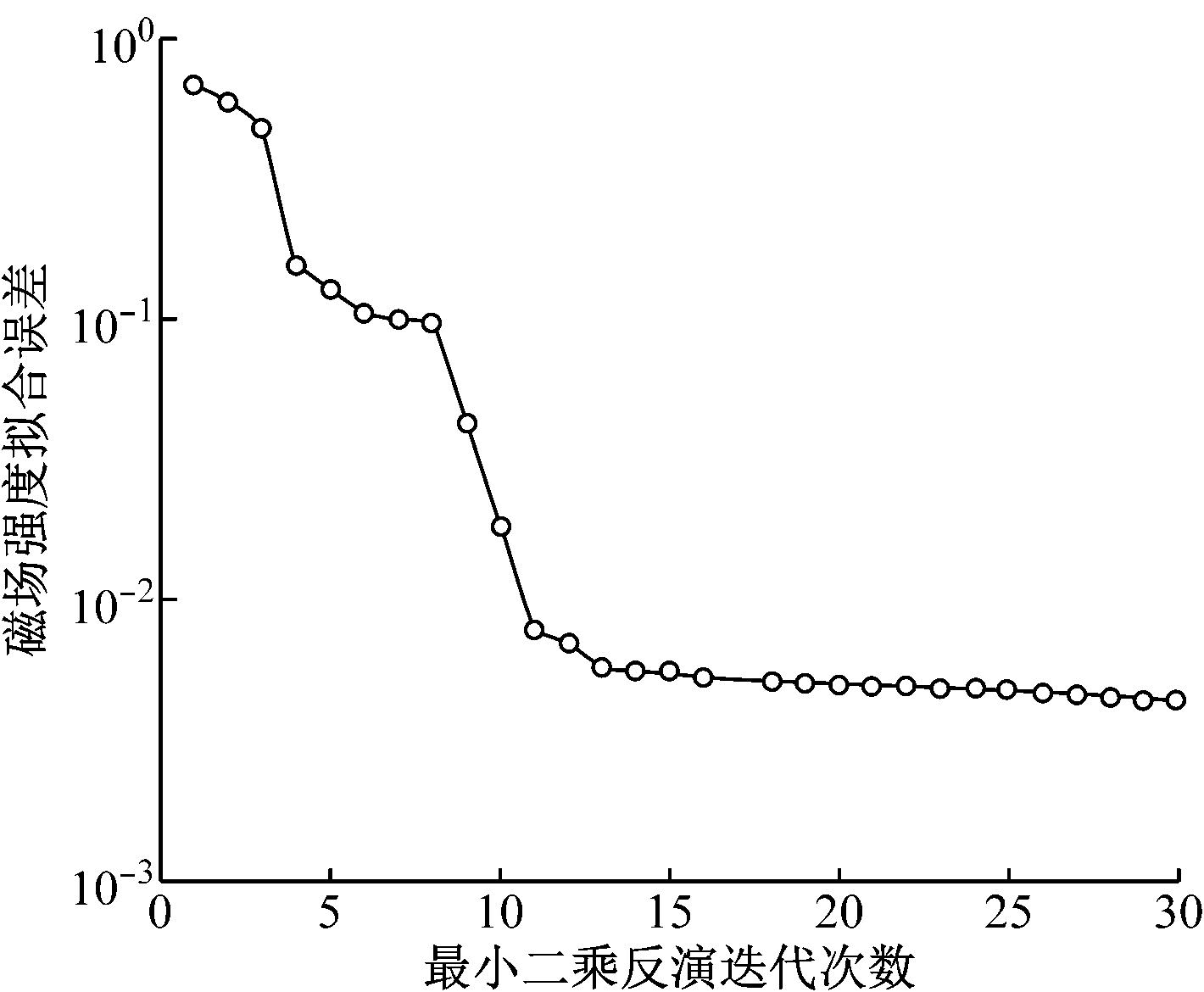
图6 磁场强度拟合误差曲线
Fig.6 Fitting error curve of magnetic field intensity
4.3 地质资料解释
全空间瞬变电磁二维反演视电阻率断面如图7所示。图7可以反映巷道顶底板岩层的电性特征,巷道顶板以上30~100 m及巷道底板以下距离巷道底部0~50 m探测范围内岩层的视电阻率值相对较高,判断为岩层不含水,这主要反映了底板以砂泥岩为主的岩性特征。巷道顶板以上20~30 m及巷道底板以下50~100 m范围内岩层的视电阻率值相对较低,低阻异常区共划分为3处:① 测点号40~70,115~195,顶板以上20~30 m探测范围;② 测点号0~145,底板以下55~100 m探测范围;③ 测点号160~200,底板以下62~100 m探测范围。上述3个低阻异常区呈层状分布,判断为岩层相对弱含水,这主要反映了底板深部砂岩含水层的特征。
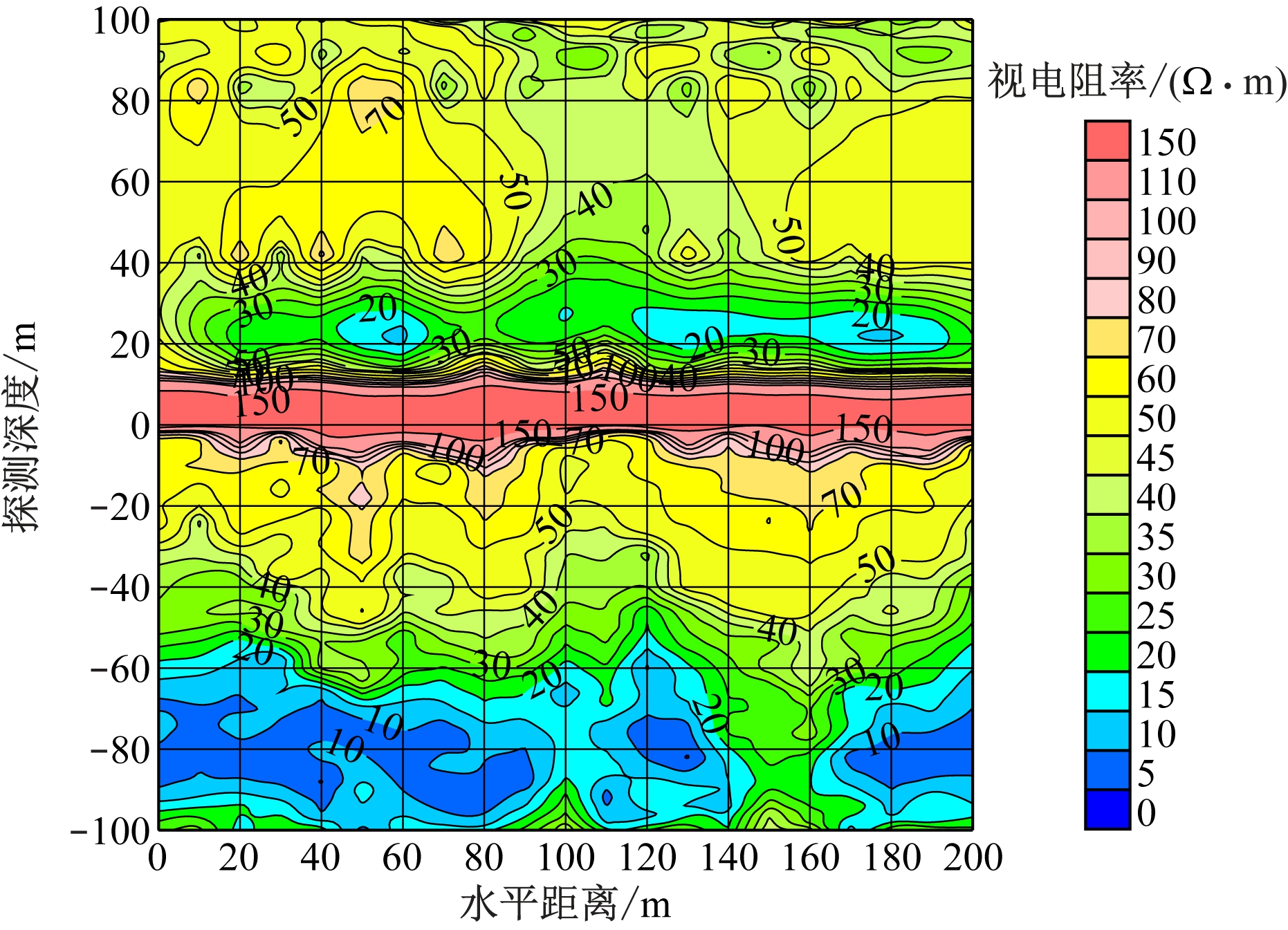
图7 全空间瞬变电磁二维反演视电阻率断面
Fig.7 Cross section of apparent resistivity inversion of
two-dimensional inversion of transient
electromagnetic in whole-space
4.4 验证情况
实测数据处理过程中加入了二维反演计算,处理结果解释后,结合煤矿井下现有巷道条件,在煤层顶板设计测线50,100,130,180 m处各布置1个钻孔,在煤层底板设计测线20,120,150 m处各布置1个钻孔,进行钻探验证,钻孔深度设计为80 m。顶板钻孔基本无出水情况,只有反演结果低阻区域的2个钻孔有滴漏水情况;底板钻孔出水量相对较大,尤其是测线20 m和120 m处的钻孔出水量为2 m3/h;测线150 m处的钻孔出水量为0.1 m3/h。验证结果表明,反演后的结果明显提高了探测精度和分辨率,对含水低阻异常区范围圈定准确,二维反演结果与实际验证情况基本吻合,反演后精度明显提高。
5 结论
(1) 介绍了全空间瞬变电磁二维反演方法的原理、流程及具体步骤,并通过粒子群算法对电阻率和地层厚度参数进行寻优。
(2) 采用Q型地电断面模型分析得出瞬变电磁场扩散规律:随着时间的增加,磁场扩散范围明显增大;因为磁场在扩散过程中不断衰减,所以靠近激发源处磁场强度值较大,远离激发源处磁场强度值较小。
(3) 在理论研究的基础上进行工程应用,对实际资料进行二维反演,分析了瞬变电磁场的扩散规律和拟合误差,解释了视电阻率探测成果,并进行了钻探验证。应用结果表明,全空间瞬变电磁二维反演方法是可行的,反演结果中的低阻异常体具有成层特性及一定的连通性,更能反映层状地层以砂泥岩为主的岩性结构特征及含水特性,提高了探测精度和分辨率。
[1] 于景邨.矿井瞬变电磁法勘探[M].徐州:中国矿业大学出版社,2007.
YU Jingcun.Mine transient electromagnetic exploration[M].Xuzhou:China University of Mining and Technology Press, 2007.
[2] 闫国才,鲜鹏辉,仇念广.深井低阻体电性源短偏移距瞬变电磁探测技术研究[J].煤炭科学技术,2020,48(6):171-176.
YAN Guocai,XIAN Penghui,QIU Nianguang.Study on short offset transient electromagnetic detection technology for low-resistance electrical sources in deep mine[J].Coal Science and Technology,2020,48(6):171-176.
[3] 程久龙,李明星,肖艳丽,等.全空间条件下矿井瞬变电磁法粒子群优化反演研究[J].地球物理学报,2014,57(10):3478-3484.
CHENG Jiulong,LI Mingxing,XIAO Yanli,et al.Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space[J].Chinese Journal of Geophysics,2014,57(10):3478-3484.
[4] 师学明,肖敏,范建柯,等.大地电磁阻尼粒子群优化反演法研究[J].地球物理学报,2009,52(4):1114-1120.
SHI Xueming,XIAO Min, FAN Jianke,et al.The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J].Chinese Journal of Geophysics,2009,52(4):1114-1120.
[5] 易远元,王家映.地球物理资料非线性反演方法讲座(十)——粒子群反演方法[J].工程地球物理学报,2009,6(4):385-389.
YI Yuanyuan,WANG Jiaying.Lecture on non-linear inverse methods in geophysical data(10)-Particle swarm optimization inversion method[J].Chinese Journal of Engineering Geophysics,2009,6(4):385-389.
[6] SEN M K, STOFFA P L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J]. Geophysics,1991,56(10):1624-1638.
[7] 姚姚.地球物理反演基本理论与应用方法[M].武汉:中国地质大学出版社,2009.
YAO Yao.Basic theory and application methods of geophysical inversion[M].Wuhan:China University of Geosciences Press,2009.
[8] NEWMAN G A,ANDERSON W L,HOHMANN G W.Interpretation of transient electromagnetic soundings over three-domensional structures for the central-loop configuration[J].Geophysical Journal International,1987,89(3):889-914.
[9] SHI Y, EBERHART R C. A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation Proceedings,Anchorage,1998.
[10] SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation,Washington,1999.
[11] 闫国才.基于粒子群算法的全空间瞬变电磁二维反演研究[D].北京:中国矿业大学(北京),2014.
YAN Guocai. Research on full-space transient electromagnetic two-dimensional inversion based on particle swarm algorithm[D]. Beijing: China University of Mining and Technology (Beijing), 2014.
[12] 李明星.全空间瞬变电磁法非线性反演研究[D].青岛:山东科技大学,2012.
LI Mingxing. Research on non-linear inversion of full-space transient electromagnetic method[D]. Qingdao: Shandong University of Science and Technology, 2012.
[13] 王青,刘云鹤,殷长春,等.基于模型空间压缩的大地电磁三维反演研究[J].地球物理学报,2019,62(2):752-762.
WANG Qing,LIU Yunhe,YIN Changchun,et al.3D MT inversion based on model space compression[J].Chinese Journal of Geophysics,2019,62(2):752-762.
[14] KRIVOCHIEVA S, CHOUTEAU M. Whole space modeling of a layered earth in time-domain electromagnetic measurements[J]. Journal of Applied Geophysics, 2002,50(4):375-391.
[15] 程久龙,黄少华,温来福,等.矿井全空间三维主轴各向异性介质瞬变电磁场响应特征研究[J].煤炭学报,2019,44(1):278-286.
CHENG Jiulong,HUANG Shaohua,WEN Laifu,et al.Response characteristics of three-dimensional axial anisotropic media for transient electromagnetic method in underground whole-space[J].Journal of China Coal Society,2019,44(1):278-286.
[16] 李明星.矿井瞬变电磁PSO-DLS组合算法反演研究[J].煤炭科学技术,2019,47(9):268-272.
LI Mingxing.Study on mine transient electromagnetic method inversion based on PSO-DLS combination algorithm[J].Coal Science and Technology,2019,47(9):268-272.
[17] 牟义,邱浩,牛超,等.多源干扰条件下瞬变电磁法电性响应规律研究[J].地球物理学进展,2019,34(6):2493-2502.
MU Yi,QIU Hao,NIU Chao,et al.Study on the electrical response law of transient electromagnetic method under multi-source interference conditions[J].Progress in Geophysics,2019,34(6):2493-2502.
