0 引言
煤矿井下通风设施、通风动力、通风网络(简称风网)结构等会随生产过程的推进而改变,使得风网分支风量发生变化[1],当变化值超过一定范围时会导致某些分支出现粉尘积聚、瓦斯超限等问题,对矿井安全生产造成极大威胁[2]。若仅靠自然分风无法满足用风分支的风量需求,需要对分支风阻进行调节。而矿井风网是个关联度很高的复杂系统,改变其中某个分支的风阻会引起整个风网变化[3],需要优化风量调节方案。众多学者对此展开深入研究,提出了多种风量调节方法。吴维权等[4]针对煤矿综放工作面采空区煤易自燃、瓦斯超限问题,提出一种增风控瓦斯和减风控火的耦合分析方法,经现场验证,该方法既有利于煤矿瓦斯治理,又能防止采空区煤自燃。崔传波等[5]针对通过改变分支风阻来重新分配风网风量会导致某些分支不能满足最小需风量的问题,采用风网解算确定被调分支风阻的可调范围,进而定量求解用风分支风量可调度。丰胜成等[6]采用灵敏度方法初步选取调节分支,并在不同调节区域采用分风优化中的通路法对初选调节分支进一步筛选,所选分支调节方便且具有经济优势。上述研究只针对单分支风量调节问题,而当用风分支需风量较大时,通过单分支调节往往无法满足要求,需通过多分支联调方式进行按需分风。针对用风分支在不同风网状态下的需风量,本文提出基于风网灵敏度矩阵来确定最优可调分支集和风阻调节范围,采用一种改进灰狼优化(Grey Wolf Optimizer,GWO)算法对矿井风量调节模型进行寻优,得出用风分支的最大可调风量,并通过矿山智能通风实验平台验证了该方案的可行性。
1 矿井风量调节建模
矿井风网在风量调节过程中需遵循节点风量平衡定律和回路风压平衡定律[7]。节点风量平衡定律方程为
(1)
式中:N,M分别为风网分支数和节点数;bij=1表示分支j风流流入节点i,bij=-1表示分支j风流流出节点i,bij=0表示节点i不是分支j的端点;Qj为分支j风量。
回路风压平衡定律方程为
![]()
(2)
式中:ckj=1表示分支j与回路k同向,ckj=-1表示分支j与回路k反向,ckj=0表示分支j不在回路k中;Rj为分支j风阻;pj为分支j中通风机风压、自然风压代数和,若无该项则取0;J为风网独立回路数,J=N-M+1。
针对矿井风网中某一特定用风分支风量供给不足问题,一般采用调阻增风方式来增大风量,需风量较小时采用单分支调阻即可,但当需风量过大时需对多条分支同时调阻。为了确定用风分支风量可调范围,以风网中用风分支风量可调最大作为风网风量调节的目标函数。
为保证矿井风网风量调节的稳定性和合理性,除了遵循节点风量平衡定律和回路风压平衡定律外,还需建立主要通风机工况点及分支风量约束条件:① 通风机实际工作风压Hf不高于最高风压Hfmax的90%。② 通风机工作效率η不低于60%。③ 风网各分支风量满足分支最小需风量Qjmin,可调分支风阻在合适的调节范围,即Rjmin≤Rj≤Rjmax,Rjmin,Rjmax分别为分支j风阻可调的最小、最大值。
由此可看出矿井风量调节模型为非线性约束模型。针对该模型中风量平衡、风压平衡及各分支最小需风量等约束条件,采用不可微精确罚函数将其转换为目标模型中的惩罚项[8],则加入惩罚项后的目标函数为
F=![]()
λ|min{0,0.9Hfmax-Hf}+min{0,η-0.6}|+
|min{0,Qj-Qjmin}|
(3)
式中:Qdt为用风分支风量;γ,λ,μ为惩罚参数,即罚因子。
2 基于风网灵敏度的风量调节
2.1 风网灵敏度求解
设分支j风阻Rj变化量ΔRj引起的分支p风量Qp变化量为ΔQp,当|ΔRj|→0时,Qp相对于Rj变化的灵敏度[9]为
(4)
通过节点风量平衡定律和回路风压平衡定律对风网中任一分支q风阻Rq求偏导,可建立分支灵敏度偏微分方程组,即

(5)
对于具有N条分支的风网,通过求解式(5)可计算出风网灵敏度矩阵:

(6)
2.2 风量调节分析
若煤矿在实际生产过程中某一用风地点(分支p)的风量小于该分支需风量,根据调阻增风原则,可选择增阻或降阻2种调节方式。由风网灵敏度矩阵性质可知,采用增阻调节方式时需选择dp,j>0的分支,采用降阻调节方式时需选择dp,j<0的分支。若分支p的风量大于该分支需风量,采用增阻调节方式时需选择dp,j<0的分支,采用降阻调节方式时需选择dp,j>0的分支。另外,在选择调阻分支时,一般选择灵敏度矩阵第p列中|dp,j|较大值对应的分支,|dp,j|越大说明对分支j调阻能够在更大程度上改变分支p的风量,或者说分支j风阻发生轻微变化时即可引起分支p的风量发生很大变化。
对大量风网数据进行实际计算与模拟分析后得出,灵敏度dp,j与风阻Rj之间呈以下关系:
![]()
(7)
式中y,x,z为常数,可通过回归方程求得,x<0。
随着分支j风阻Rj增大,灵敏度dp,j不断减小,即风量Qp变化幅度减小。当Rj超过临界值Rjmax时,风量Qp变化幅度很小,即风量调节进入迟钝区域;当Rj<Rjmax时,由于Qp随Rj的变化较为灵敏,可认为Rj对Qp的增阻调节处于灵敏状态。因此,通过分支j对Qp进行增阻调节的合理范围为[Rj0,Rjmax](Rj0为风网未进行风量调节时分支j的初始风阻)。对大量风网风量调节数据分析后得出,Rjmax可通过下式设置:
![]()
(8)
3 改进GWO算法
3.1 GWO算法
GWO算法是一种新型智能优化算法[10],是受灰狼种群的社会等级和狩猎行为启发得到的。灰狼种群通过跟踪、环绕逼近方式寻找猎物,其数学模型为
D(t)=|CX′(t)-X(t)|
(9)
X(t+1)=X′(t)-AD(t)
(10)
式中:D(t)为第t次迭代后猎物与灰狼之间的位置差值;C,A为控制参数;X′(t),X(t)分别为第t次迭代后猎物的位置和灰狼个体位置。
(11)
C=2r2
(12)
式中:a为控制因子,在迭代过程中由2递减到0;r1,r2为[0,1]间随机数;Tmax为最大迭代次数。
高等级个体α,β,δ在进攻阶段负责定位猎物,并指引其他灰狼个体完成靠近、攻击等行为。该过程通过式(9)、式(10)计算出其他灰狼个体与α,β,δ之间的距离(分别为X1(t),X2(t),X3(t)),并根据下式更新灰狼种群的个体位置。
X(t+1)=(X1(t)+X2(t)+X3(t))/3
(13)
3.2 改进GWO算法
GWO算法具有优化精度高、收敛速度快等特点,但在单独求解复杂优化问题时易出现早熟现象[11-12]。为了提高GWO算法的全局搜索能力和优化精度,对GWO算法进行改进,具体如下。
(1) 采用佳点集初始化种群。GWO算法采用随机生成方法初始化种群,种群个体很难遍历搜索空间,在一定程度上影响了算法的搜索效率。
佳点集是一种有效的均匀选点方法[13],已成功应用于遗传算法、粒子群优化算法(Particle Swarm Optimization,PSO)等智能优化算法中。与随机初始化种群相比,佳点集可使初始种群均匀分布在搜索空间,增加种群的多样性,有助于改善算法的全局搜索能力。因此,采用佳点集对GWO算法进行种群初始化。
(2) 与差分进化(Differential Evolution,DE)算法融合。DE算法是基于种群进化而提出的一种高效全局优化算法[14],具有控制参数少、执行简单、鲁棒性强等特点,可更好地处理搜索距离较长的优化问题。DE算法包括变异、交叉、选择3种操作。
采用DE/rand/1变异策略实现变异操作,即
Xd(t+1)=Xr1(t)+R(Xr2(t)-Xr3(t))
(14)
式中:Xd(t+1)为变异后灰狼个体的位置;Xr1(t),Xr2(t),Xr3(t)为灰狼个体r1,r2,r3的位置,r1,r2,r3为[1,N1]内的随机整数,且r1≠r2≠r3,N1为种群规模;R为缩放因子,取值范围为[0,1]。
采用二项式交叉策略实现交叉操作,即
![]()
(15)
式中:Xc(t+1)为交叉后的灰狼个体位置;hr为随机交叉概率;h为交叉概率。
采用贪婪算法实现选择操作,即
(16)
式中:Xs(t+1)为经选择后的灰狼个体位置;f(·)为优化目标函数。
(3) 优化非线性控制参数。在GWO算法中,A为表征全局勘探和局部开采的重要参数,|A|>1表示灰狼个体搜寻猎物过程,|A|<1表示灰狼个体围捕猎物过程。由式(11)可知,A可通过控制因子a调节,因此对a进行优化设计:
a=2[1-(t/Tmax)2]
(17)
a优化前后对比如图1所示。可看出优化后的a在迭代前期变化缓慢,以尽可能寻找全局最优解,在迭代后期变化幅度较大,可改善局部搜索,加快算法寻优速度。

图1 控制因子a优化前后对比
Fig.1 Comparison of a before and after optimization
根据上述改进策略,改进GWO算法流程如下。
Step1:设置算法种群规模、最大迭代次数、寻优维数、交叉概率、缩放因子等参数。
Step2:采用佳点集初始化灰狼种群。
Step3:计算种群个体的适应度并按降序排列,将适应度前3位的个体位置记为Xα,Xβ,Xδ。
Step4:更新参数a,A,C。
Step5:通过变异、交叉操作产生新的子代种群,再经选择操作选出父代和子代种群中更优的个体进入下一代种群。
Step6:不断进行迭代计算,若当前迭代次数t<Tmax,转至Step3继续执行;若t=Tmax,则终止迭代,输出最优位置,并求得函数最优值。
4 矿井风量优化调节实验
4.1 实验平台
基于矿山智能通风实验平台进行风量调节研究。该平台参照某矿风网拓扑结构以4∶1的比例搭建,如图2所示。风网模拟“一矿两面”结构,巷道为上下2层对称结构,配置10余个智能风门风窗调节装置,在关键分支中配置矿用高精度传感器,以采集通风参数。

图2 实验平台风网巷道
Fig.2 Ventilation network tunnel of experiment platform
在实验平台中搭建矿井智能通风控制中心,其主要由电源高压控制柜、PLC控制柜、人工操控平台、上位机监测平台组成,可实现井下通风环境监测、工业以太网通信、地面远程监控和风量智能调节等功能。
4.2 风量调节分支优化
假设矿井安全监控系统检测到井下分支14的瓦斯体积分数为1.5%(一般低于1%认定为通风安全),若采用调阻增风方式增加分支14的风量,需要基于风网灵敏度对风量调节分支进行优化选择。
实验平台风网拓扑如图3所示。该风网中共有15个节点、21条分支、7条独立回路,箭头表示分支风流流向,出风节点 与进风节点①之间的伪分支21以虚线表示,伪分支21风阻为0。通风机位于分支20,通风机风压特性曲线为Hf=2 897.93+17.24Q-0.5Q2,其中Q为通风机风量。
与进风节点①之间的伪分支21以虚线表示,伪分支21风阻为0。通风机位于分支20,通风机风压特性曲线为Hf=2 897.93+17.24Q-0.5Q2,其中Q为通风机风量。

图3 风网拓扑
Fig.3 Ventilation network topology
风网初始参数见表1。实际矿井风网受巷道位置、环境及其他条件的限制,无法实现所有分支均可调节。对于该实验平台,分支1,2,3,9,11,13,14,19,20,21均不具有可调节性。
基于Matlab自制的风网灵敏度矩阵计算程序,得出实验平台风网灵敏度矩阵,如图4所示。每列数据表示风网各分支的风阻变化对该分支风量的影响程度,每行数据表示该分支的风阻变化对各分支风量的影响程度。
表1 风网初始参数
Table 1 Initial parameters of ventilation network

分支风阻/(N·s2·m-8)初始风量/(m3·s-1)最小风量/(m3·s-1)是否可调10.4643.2741.92不可调20.1222.8019.43不可调30.2120.4716.85不可调41.087.896.14可调50.0414.9111.26可调60.2010.887.29可调71.169.596.65可调81.385.482.59可调90.359.437.34不可调100.653.932.12可调110.331.521.24不可调120.429.366.07可调130.345.494.26不可调141.215.465.46不可调150.1410.986.71可调160.2114.829.94可调170.3018.8612.42可调180.0724.4120.38可调190.1343.2741.92不可调200.7343.2741.92不可调21043.2741.92不可调

图4 风网灵敏度矩阵
Fig.4 Sensitivity matrix of ventilation network
采用风网灵敏度理论对风量调节分支进行优化选择。根据图4得出不同分支调阻对分支14风量的灵敏度,见表2。
若通过增阻调节方式增大分支14风量,需选择可调分支中灵敏度d14,j>0的分支进行调节。将表2中d14,j>0的分支按灵敏度降序排列,为12,17,15,7,13,4,8,由于分支13不具有可调性且分支4,8调阻对分支14风量变化的灵敏度较其他可调分支小得多,对风量调节的贡献度不足,同时考虑减小风量调节对风网工作状态的影响程度,选择分支12,17,15,7作为最优可调分支集。对选出的4个可调分支,依次计算分支风阻设定为不同值时对应的灵敏度,见表3。
表2 不同分支调阻对分支14风量的灵敏度
Table 2 Sensitivity of different branches to adjust wind
resistance to air volume of branch 14

分支灵敏度分支灵敏度分支灵敏度1-1.822 880.012 6 150.837 72-0.445 89-0.243 816-3.528 73-0.048 510-0.143 5172.994 840.091 0 11-0.097 918-5.592 55-0.516 1123.100 019-1.822 86-0.805 1130.197 520-1.822 870.613 914-1.532 221-1.822 8
表3 灵敏度随可调分支风阻变化数据
Table 3 Sensitivity change data with wind resistances
of adjustable branches
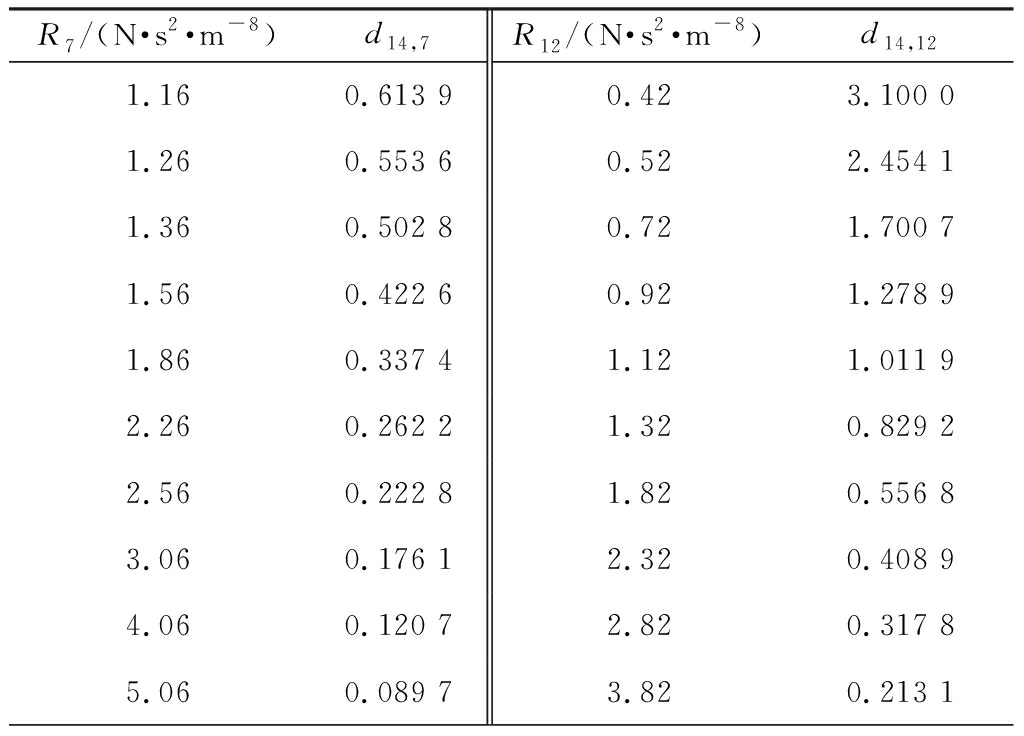
R7/(N·s2·m-8)d14,7R12/(N·s2·m-8)d14,121.160.613 90.423.100 01.260.553 60.522.454 11.360.502 80.721.700 71.560.422 60.921.278 91.860.337 41.121.011 92.260.262 21.320.829 22.560.222 81.820.556 83.060.176 12.320.408 94.060.120 72.820.317 85.060.089 73.820.213 1

R15/(N·s2·m-8)d14,15R17/(N·s2·m-8)d14,170.140.837 70.302.994 80.240.668 90.452.053 10.340.553 30.651.412 90.540.405 90.950.934 60.840.284 11.350.623 61.240.197 91.850.427 11.540.159 22.350.317 52.040.118 12.850.248 83.040.075 13.350.202 15.040.040 73.850.168 6
将表3中每个分支的10组数据通过Matlab软件的Power幂函数进行拟合处理,得到灵敏度随风阻变化曲线,其中d14,7随风阻R7的变化曲线如图5所示。
通过图5可求得d14,7和R7之间的函数关系:
![]()
(18)

图5 灵敏度d14,7随风阻R7变化曲线
Fig.5 Variation curve of sensitivity d14,7 with
wind resistance R7
根据式(8)可求得分支7调阻的合理范围为1.16~6.55 N·s2/m8。
同理可求出灵敏度随分支12,15,17风阻变化的函数关系及调阻合理范围,见表4。
表4 灵敏度与分支风阻的函数关系及调阻范围
Table 4 Function relationship between sensitivity
and wind resistance of branch and adjustment
range of wind resistance
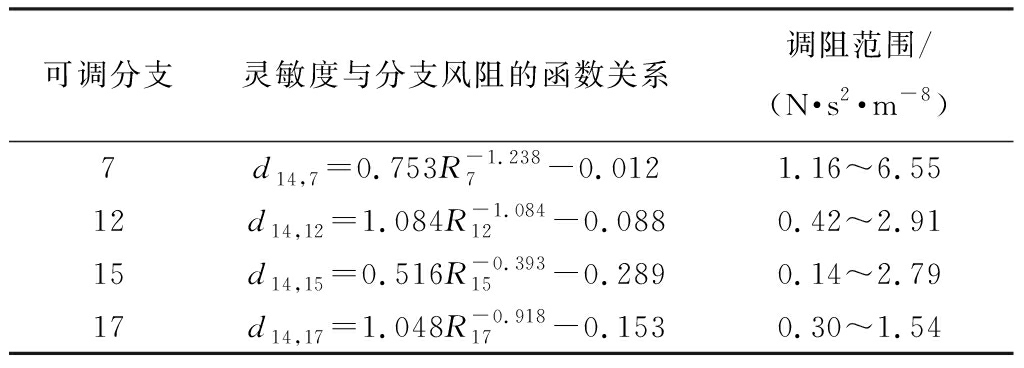
可调分支灵敏度与分支风阻的函数关系调阻范围/(N·s2·m-8)7d14,7=0.753R-1.2387-0.0121.16~6.5512d14,12=1.084R-1.08412-0.0880.42~2.9115d14,15=0.516R-0.39315-0.2890.14~2.7917d14,17=1.048R-0.91817-0.1530.30~1.54
4.3 可调风量优化分析
确定对分支14风量调节的最优可调分支集和风阻调节范围后,分别采用GWO算法、PSO算法和改进GWO算法求解分支14的最大可调风量,确定分支14的最大可调风量范围。3种算法的主要参数设置:种群规模为30,优化变量维数为4,最大迭代次数为200,交叉概率为0.2。为了避免寻优效果存在偶然性,采用3种算法分别对模型优化30次,结果见表5。
表5 3种算法优化结果
Table 5 Optimization results of three algorithms

指标PSO算法GWO算法 改进GWO算法 风量优化平均值/(m3·s-1) 9.7610.3410.72风量最优解/(m3·s-1)9.8910.4510.83平均收敛代数13187106平均运行时间/s14.2517.3922.13
从表5可看出,基于改进GWO算法求解分支14风量的优化平均值和最优解均优于GWO算法、PSO算法,平均收敛代数高于GWO算法、小于PSO算法。改进GWO算法总体优化效果最佳,表现出更好的勘探能力,有效避免了局部最优。
3种算法某次仿真结果如图6所示。可看出改进GWO算法对分支14的最大调节风量达10.78 m3/s。此时调节分支的风阻分别为R7=5.64 N·s2/m8,R12=2.91 N·s2/m8,R15=0.31 N·s2/m8,R17=0.74 N·s2/m8,经风网解算验证,风量调节后其他分支风量满足最小需风分配要求,由此得到分支14风量可调范围为5.46~10.78 m3/s。
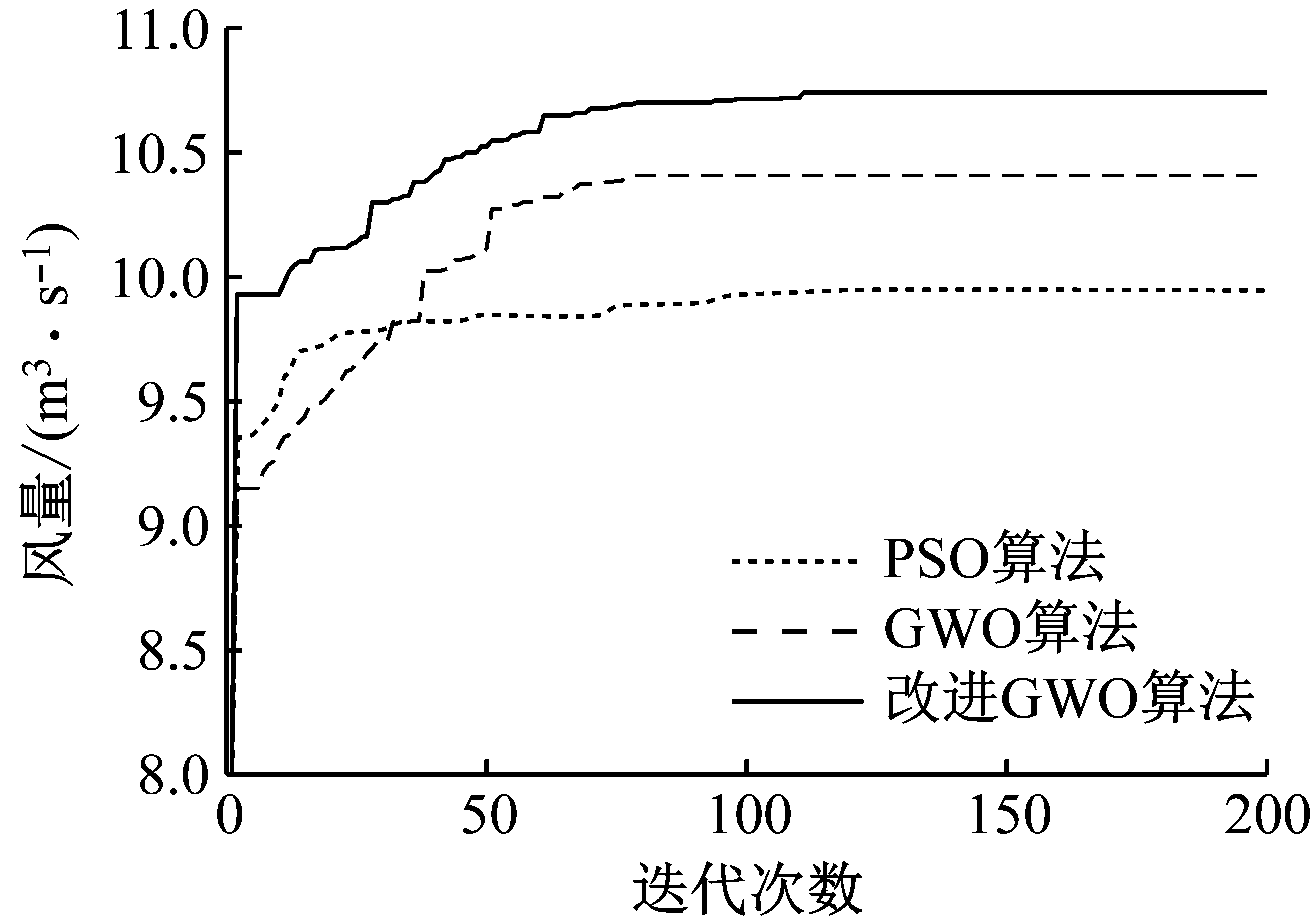
图6 分支14风量适应度曲线
Fig.6 Fitness curves of air volume of branch 14
针对实际矿井风网,可根据分支14的需风量对可调分支的灵敏度大小采取不同的调节方法,优先选择灵敏度大的分支进行调节。在不同的可调分支数下,分支14的最大可调风量见表6。
表6 可调分支数不同时分支14最大可调风量
Table 6 The maximum adjustable air volume of
branch 14 under different number of adjustable branches

可调分支数调节分支最大可调风量/(m3·s-1)1127.19212,178.51312,15,179.4647,12,15,1710.78
4.4 实验验证
将瓦斯注入实验平台分支14中至瓦斯体积分数为1.5%,此时安装在分支14中的瓦斯传感器检测到当前环境中瓦斯浓度超限,将通风异常情况反馈至上位机监测平台进行分析,之后得出最优风量调节方案,向智能风门风窗调节装置发出控制指令进行风量调节操作。若上位机监测平台优先采用增阻调节方式来增大分支14风量,使瓦斯体积分数降至0.8%,通过计算可得分支14的最小风量为8.26 m3/s。由表6可知,当只对分支12进行调阻时,分支14的最大可调风量为7.19 m3/s,不满足风量调节要求,而对分支12,17进行联调增阻时,分支14的最大可调风量为8.51 m3/s,符合风量调节需求,此时R12=2.48 N·s2/m8,R17=0.63 N·s2/m8。风量调节后上位机监测界面如图7所示,通过分支14中安装的风速传感器读取Q14=8.48 m3/s,满足矿井安全生产的分支需风要求,验证了智能风量调节方案的可行性。

图7 上位机监测界面
Fig.7 Monitoring interface of host computer
5 结论
(1) 为了满足矿井风网某一特定用风分支的风量需求,以用风分支风量可调最大为目标,建立了矿井风量调节模型。为了确定最优的风量调节方案,采用风网灵敏度矩阵选择最优可调分支集和风阻调节范围,并基于改进GWO算法实现寻优。优化结果表明,采用改进GWO算法得到的风量优化平均值和最优解均优于GWO,PSO算法。
(2) 提出了一种根据分支需风量选择不同调节分支数的智能风量调节方案,并基于矿山智能通风实验平台进行验证。结果表明,在满足其他分支最小需风量的条件下,调节后的分支风量满足矿井安全风量要求,验证了智能风量调节方案的可行性和实用性。
[1] BASCOMPTA M,SANMIQUEL L,ZHANG H.Airflow stability and diagonal mine ventilation system optimization:a case study[J].Journal of Mining Science,2018,54(5):813-820.
[2] 王凯,郝海清,蒋曙光,等.矿井火灾风烟流区域联动与智能调控系统研究[J].工矿自动化,2019,45(7):21-27.
WANG Kai,HAO Haiqing,JIANG Shuguang,et al.Research on regional linkage and intelligent control system of mine fire wind-smoke flow[J].Industry and Mine Automation,2019,45(7):21-27.
[3] CHATTERJEE A,ZHANG Lijun,XIA Xiaohua.Optimization of mine ventilation fan speeds according to ventilation on demand and time of use tariff[J].Applied Energy,2015,146(15):65-73.
[4] 吴维权,魏国山,吕明飞.基于风量调节的高瓦斯易自燃矿井火灾与瓦斯治理[J].煤炭科学技术,2013,41(9):109-111.
WU Weiquan,WEI Guoshan,LYU Mingfei.Mine fire and gas control in high gassy and spontaneous combustion mine based on ventilation quantity adjustment[J].Coal Science and Technology,2013,41(9):109-111.
[5] 崔传波,蒋曙光,王凯,等.基于风量可调度的矿井风量调节[J].工矿自动化,2016,42(2):39-43.
CUI Chuanbo,JIANG Shuguang,WANG Kai,et al.Adjustment of mine air volume based on air volume dispatchable model[J].Industry and Mine Automation,2016,42(2):39-43.
[6] 丰胜成,付华.矿井通风网络风量调节分支的优化选择[J].辽宁工程技术大学学报(自然科学版),2019,38(6):513-516.
FENG Shengcheng,FU Hua.The optimal selection of air flow adjustment branch of mine ventilation network[J].Journal of Liaoning Technical University (Natural Science Edition),2019,38(6):513-516.
[7] 李宗翔.有源风网模型及其应用计算[J].煤炭学报,2010,35(增刊1):118-122.
LI Zongxiang.Containing the source ventilation network model and its application[J].Journal of China Coal Society,2010,35(S1):118-122.
[8] 贾进章,刘剑,倪景峰.通风系统可靠性稳定性及灵敏性数学模型[J].辽宁工程技术大学学报,2003,22(6):725-727.
JIA Jinzhang,LIU Jian,NI Jingfeng.Mathematical models for reliability stability and sensitivity of ventilation system[J].Journal of Liaoning Technical University,2003,22(6):725-727.
[9] ANTCZAK T.A lower bound for the penalty parameter in the exact minimax penalty function method for solving non-differentiable extremum problems[J].Journal of Optimization Theory and Applications,2013,159(2):437-453.
[10] MIRJALILI S,MIRJALILI S M,LEWIS A.Grey wolf optimizer[J].Advances in Engineering Software,2014,69(3):46-61.
[11] SAREMI S,MIRJALILI S Z,MIRJALILI S M.Evolutionary population dynamics and grey wolf optimizer[J].Neural Computing and Applications,2015,26(5):983-989.
[12] ZHU Aijun,XU Chuanpei,LI Zhi,et al.Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J].Journal of Systems Engineering and Electronics,2015,26(2):317-328.
[13] 陈义雄,梁昔明,黄亚飞.基于佳点集构造的改进量子粒子群优化算法[J].中南大学学报(自然科学版),2013,44(4):1409-1414.
CHEN Yixiong,LIANG Ximing,HUANG Yafei.Improved quantum particle swarm optimization based on good-point set[J].Journal of Central South University(Science and Technology),2013,44(4):1409-1414.
[14] QIN A K,HUANG V L,SUGANTHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization[J].IEEE Transactions on Evolutionary Computation,2009,13(2):398-417.
