0 引言
放顶煤过程的智能化是制约智能化综放开采的主要技术瓶颈[1-2]。在放顶煤过程中,根据煤层赋存条件变化进行煤矸精准识别,并根据识别结果实时自动调整放煤口启闭,是实现自动化放煤的关键[3],不仅能够降低混矸率,提高煤炭质量,还能使放煤工人远离综放工作面,减少恶劣环境对工人健康的影响。
对放顶煤过程中产生的振动信号进行辨识是实现煤矸识别的有效手段之一。近年来,学者们针对该方法进行了大量研究。文献[4]分析了煤和矸石冲击产生的振动信号频谱特征,得出了2种振动信号频率不同的结论,但未根据频谱特征进一步研究煤矸识别技术。文献[5]分析了放顶煤过程中液压支架后尾梁及刮板输送机处采集的振动信号,认为液压支架后尾梁更适合作为煤矸冲击振动信号测点,进一步分析了不同工况下振动信号的时域特征,得出了方差、偏度与峭度指标对工况变化敏感的结论,但放顶煤过程的复杂性使得尾梁振动信号具有非平稳特性,时域特征不能准确地表征振动信号。文献[6]采用小波分析方法对煤和矸石冲击产生的振动信号进行特征提取,设计了神经网络模型实现煤矸识别,但建模时使用的训练样本和测试样本较少,模型有效性有待进一步验证。
本文提出了一种基于经验模态分解(Empirical Mode Decomposition,EMD)特征提取和随机森林(Random Forest,RF)的煤矸识别方法。该方法对综放现场采集的大量煤和矸石冲击液压支架尾梁产生的振动样本信号进行EMD,在分解产生的本征模态函数(Intrinsic Mode Function,IMF)上进行特征提取与筛选,形成最优化的特征数据集训练RF模型,提高了煤矸识别的准确性;与BP神经网络、支持向量机等机器学习算法相比,采用的RF算法可直接对特征数据集进行分类,无需进一步处理,保证了煤矸识别效率。
1 基于EMD的特征提取
1.1 EMD基本原理
EMD是N. E. Huang等[7-8]在对瞬时频率概念研究基础上提出的一种自适应分解的信号处理方法,在机械故障诊断[9]、模态参数识别[10]等工程领域得到了广泛应用。EMD可将信号中不同时间尺度的波动逐级分解出来,产生一系列IMF。各个IMF需满足2个条件[11]:① 数据序列中极值点和过零点最多相差1个。② 任一时刻由信号的局部极大值与局部极小值定义的包络平均值为0。原始信号S经EMD后可表示为
(1)
式中:n为分解得到的IMF个数;cj为第j个IMF;r为残差信号,代表信号的平均趋势。
1.2 特征提取
为了获取表征原始信号的特征向量,对各样本信号进行EMD,根据分解结果选取有效IMF,进一步提取IMF能量、峭度、矩阵奇异值及对应的熵作为特征向量,并对各特征向量的提取效率及有效性进行比较,完成特征筛选,建立特征数据集。
IMF能量为
(2)
式中:N为样本包含的数据点数;m为有效IMF个数;cj(i)为第j个有效IMF的第i个数据点。
IMF峭度为
(3)
式中:E(·)为期望函数;μj为第j个有效IMF的均值;σj为第j个有效IMF的标准差。
根据奇异值分解定义[12],可对各有效IMF组成的m×N矩阵C进行奇异值分解:
C=UQVH
(4)
式中:U,V分别为m阶、N阶酉矩阵;![]() 为矩阵C的秩,ω1,ω2,…,ωr为矩阵C的奇异值,ω1≥ω2≥…≥ωr>0。
为矩阵C的秩,ω1,ω2,…,ωr为矩阵C的奇异值,ω1≥ω2≥…≥ωr>0。
信息熵是系统不确定性的定量评价指标[13-15],可表征信号分布状态的不确定性和复杂程度。对于包含m个元素的离散随机变量X={x1,x2,…,xm},令第j个元素出现的概率为![]() 则X的信息熵定义为
则X的信息熵定义为
(5)
依据式(5),可求得IMF能量熵、奇异值熵及峭度熵。
2 RF原理
RF的实质是一个包含多棵决策树的组合分类器,在一定程度上克服了单分类器的局限性[16-17],通过集成提高了分类器的稳定性。RF采用Bootstrap方法进行重采样[18],产生多个训练集;利用每个训练集生成对应的决策树,在构建决策树时采用随机分裂属性集方法。使用训练好的RF模型可直接对特征数据集进行分类,简化了计算环节,减少了特征提取耗时。
2.1 Bootstrap重采样
设集合T中有k个样本,若每次有放回地从该集合中抽取1个样本,抽取k次形成的新集合T*中不包含第t(t=1,2,…,k)个样本的概率为
(6)
当k趋于无穷时,有
(7)
由式(7)可知,虽然T*与T中样本数均为k,但T*中可能包含了重复样本,且T*中约包含T中63.2%的样本。
2.2 RF算法流程
RF算法流程如图1所示。

图1 RF算法流程
Fig.1 RF algorithm flow
采用Bootstrap方法对特征数据集进行重采样,产生s个训练集。之后利用训练集生成对应的决策树,在每个非叶子节点选择分裂属性之前,从特征数据集中随机抽取q个特征作为当前节点的分裂属性。使每棵树完整生长,不进行剪枝操作,最终所有决策树构成一个RF。当有测试集样本输入时,RF中每棵决策树都会输出一个结果,采用投票方法将s棵决策树中输出最多的类别作为测试集样本的类别输出。
3 煤矸识别流程
基于EMD特征提取和RF的煤矸识别流程如图2所示。首先,对放顶煤过程中采集的振动信号进行等长度截取预处理,得到一系列放煤和放矸石振动样本信号;其次,对各样本信号进行EMD,根据分解结果选取有效IMF,提取IMF能量、矩阵奇异值、峭度及对应的熵作为特征向量;再次,使用各特征向量独立训练RF模型,并将测试集样本数据输入训练好的RF模型测试特征向量的有效性,根据识别结果完成特征向量筛选,建立特征数据集;最后,使用特征数据集训练RF模型,通过训练好的RF模型实现煤矸识别。
图2 煤矸识别流程
Fig.2 Coal and gangue identification flow
4 煤矸识别试验
4.1 数据采集
煤矸识别试验使用的放煤和放矸石振动信号来源于同煤大唐塔山煤矿有限公司8222综放工作面。工作面全长230.5 m,平均煤层厚度为14.36 m。夹矸6~17层,夹矸单层厚度为0.05~0.82 m。各可采煤层的物理性质相似,呈碎块状、块状、条带状结构,弱玻璃光泽,水平层理,煤层坚固性系数为2.7~3.7。夹矸多为灰褐色高岭岩、灰白色高岭质泥岩、灰黑色炭质泥岩,坚固性系数为4.0~4.5。
采用1A946E型IEPE压电式加速度传感器及DH5925N型便携式数据采集仪对放顶煤过程中顶煤和矸石冲击ZF17000/27.5/42D型液压支架尾梁产生的振动信号进行采集与记录。仪器设置位置如图3所示。采用螺纹安装方式将加速度传感器安装在液压支架尾梁背面,并通过信号线将加速度传感器与数据采集仪连接,如图4所示。数据采集仪布置在液压支架两立柱之间,如图5所示。
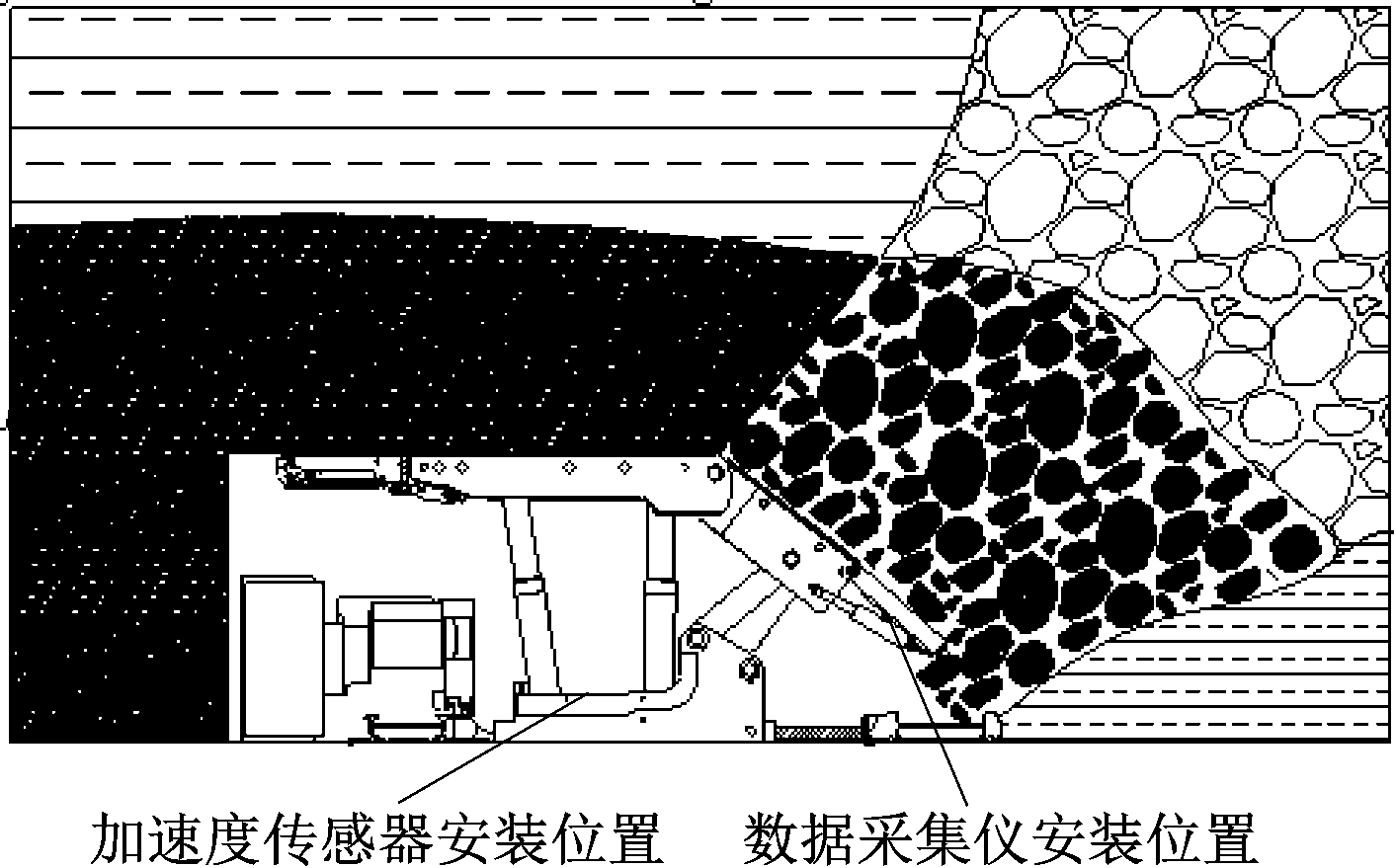
图3 振动采集仪器布置
Fig.3 Arrangement of vibration acquisition instruments

图4 加速度传感器安装现场
Fig.4 Installation site of acceleration sensor

图5 数据采集仪安装现场
Fig.5 Installation site of data acquisition
试验开始时,将数据采集仪的采样频率设置为25.6 kHz,采集并存储放顶煤过程中煤和矸石冲击液压支架产生的振动信号,并根据放煤工人的提示记录放煤和放矸石2种工况的开始及结束时刻。放煤和放矸石振动信号时域波形如图6所示。
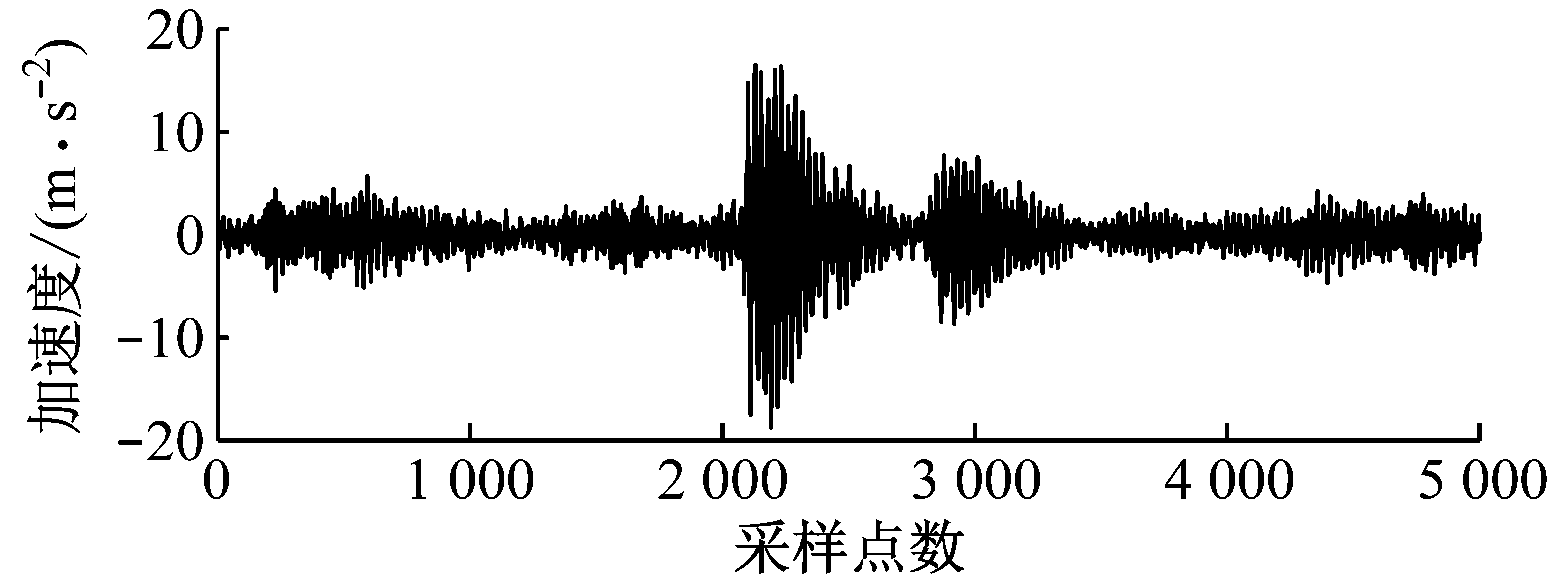
(a) 放煤振动信号
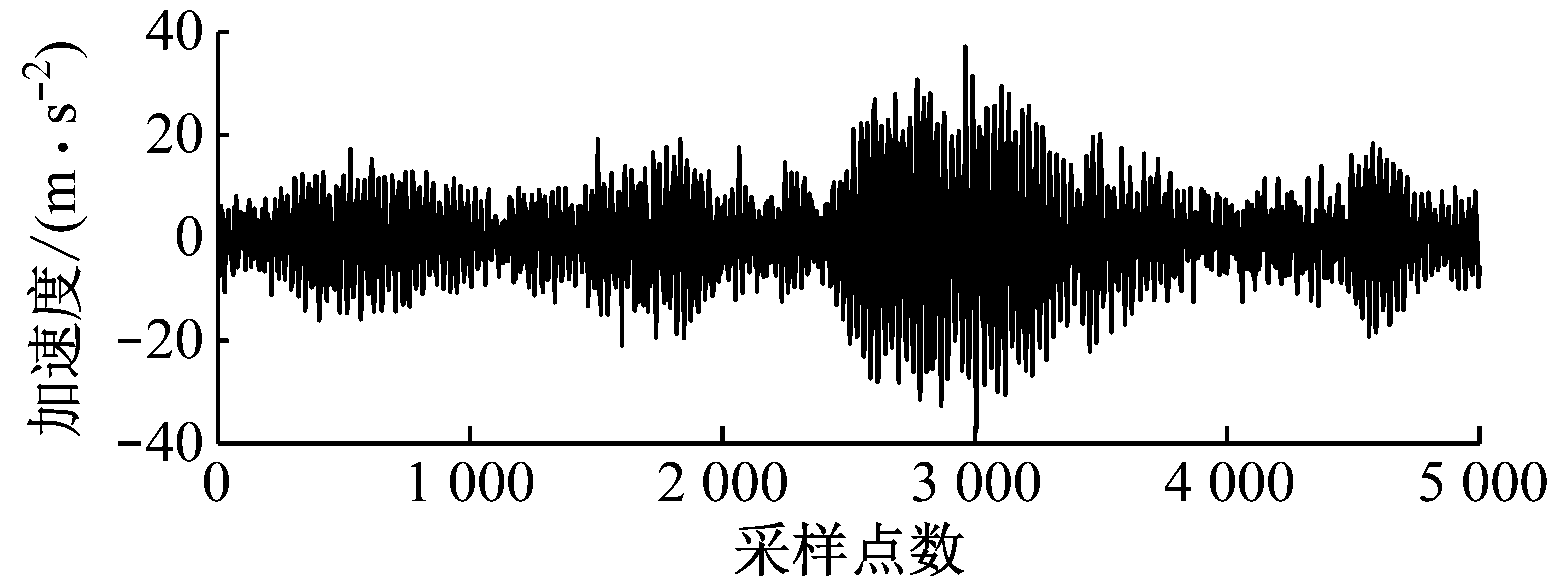
(b) 放矸石振动信号
图6 振动信号时域波形
Fig.6 Temporal waveforms of vibration signals
4.2 振动信号特征提取及特征数据集构建
对放顶煤过程中采集的放煤和放矸石2种工况下的振动信号进行EMD,结果如图7所示。可看出2种振动信号经EMD后各得到10个IMF及1个残差分量,且对应的IMF幅值和波形具有明确区别。另外放煤和放矸石振动信号的能量均集中在前8个IMF中,因此将前8个IMF作为有效IMF,提取IMF能量、峭度、矩阵奇异值及对应的熵作为特征向量。
对采集的原始振动信号进行预处理,以5 000点作为1个样本长度,共得到放煤和放矸石振动信号各1 100个样本数据。从原始样本中随机抽取放煤和放矸石振动信号各1 000个样本作为训练集、100个样本作为测试集,将放煤状态标签设置为1、放矸石状态标签设置为0,进行RF模型训练及测试。

(a) 放煤振动信号
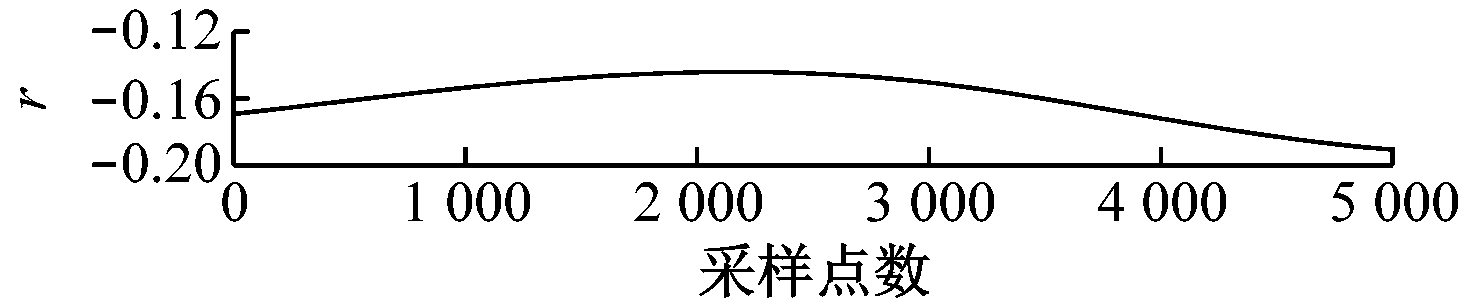
(b) 放矸石振动信号
图7 振动信号EMD结果
Fig.7 EMD results of vibration signals
为验证所提取特征的有效性,使用各特征向量分别训练RF模型。设置RF所含决策树数量s=500,分裂属性集中属性个数q=M/2(M为特征总数)。为保证识别结果的可靠性,每次均使用随机产生的训练集及测试集进行建模及识别,并将10次识别的准确率平均值作为最终结果。采用不同特征向量进行RF建模及识别的结果见表1。
表1 采用不同特征向量的煤矸识别结果
Table 1 Coal and gangue identification results by use of different feature vectors

特征识别准确率/%放煤放矸石平均值IMF能量91.697.094.30IMF能量+IMF能量熵94.197.295.65IMF峭度63.786.875.25IMF峭度+IMF峭度熵64.686.875.70IMF矩阵奇异值88.385.486.85IMF矩阵奇异值+IMF奇异值熵90.084.787.35
由表1可知,使用IMF能量训练得到的RF模型对测试集样本的识别准确率最高,达94.30%;采用IMF峭度训练得到的RF模型识别准确率最低,仅为75.25%;各特征向量加入对应的熵特征再进行训练得到的RF模型识别准确率均小幅提升。将IMF峭度特征剔除,使用IMF能量(8维)、IMF能量熵(1维)、IMF矩阵奇异值(8维)、IMF奇异值熵(1维)共18维数据建立特征数据集,由特征数据集训练得到的RF模型对放煤和放矸石各100组振动样本的识别准确率达96.5%。
4.3 RF模型性能评估
RF模型决策树数量对其泛化性能有一定影响。为获得RF模型的最优决策树数量,对包含不同数量决策树的RF模型进行评估。具体方法:设置步长为50,使决策树数量在50~1 000范围内变动;对于每个确定的决策树数量,均使用4.2节中得到的特征数据集建立100个RF模型,取其识别结果的平均值作为当前RF模型的识别准确率。决策树数量不同的RF模型识别准确率如图8所示。可看出当决策树数量设置为100或150时,RF模型识别效果最优,此时对测试集样本的识别准确率达97%。
考虑到综放工作面煤矸识别的实时性需求,对特征数据集中各特征向量的提取耗时及RF模型对测试集样本的识别耗时进行统计。具体方法:从测试集样本中随机抽取10组数据,统计10组数据特征提取的平均耗时;将10组数据特征向量输入RF模型,计算其平均识别耗时。统计结果见表2。

图8 决策树数量对RF模型识别性能的影响
Fig.8 Influence of decision tree number on RF identification performance
表2 特征提取及识别耗时统计
Table 2 Time consuming statistics of feature extraction and identification
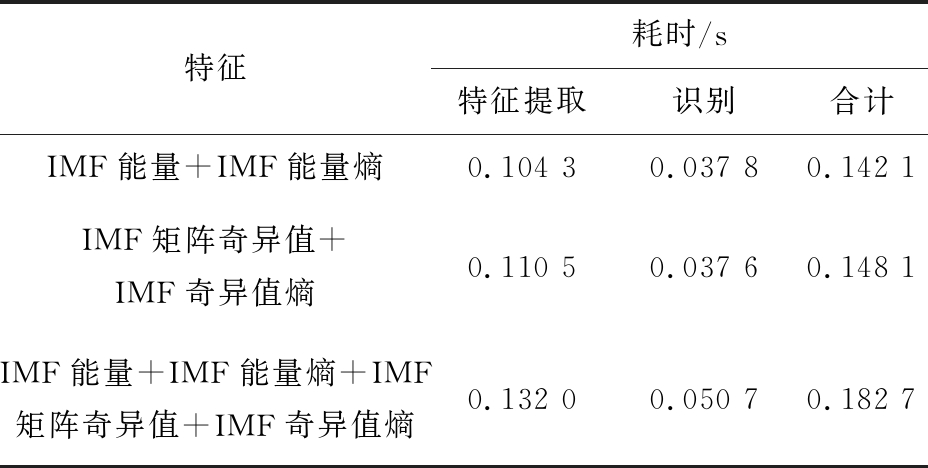
特征耗时/s特征提取识别合计IMF能量+IMF能量熵0.104 30.037 80.142 1IMF矩阵奇异值+IMF奇异值熵0.110 50.037 60.148 1IMF能量+IMF能量熵+IMF 矩阵奇异值+IMF奇异值熵0.132 00.050 70.182 7
由表2可知,使用IMF能量及其熵组成的特征向量训练RF模型时,模型对测试集样本进行特征提取与识别的耗时为0.142 1s,使用IMF矩阵奇异值及其熵组成的特征向量训练时耗时为0.148 1s,使用组合特征向量训练时耗时为0.182 7 s。
5 结论
(1) 在综放现场采集了大量的煤、矸石冲击液压支架尾梁产生的振动信号,对振动信号进行EMD,采用IMF能量、峭度、矩阵奇异值及对应的熵对振动信号进行定量描述,并采用不同的特征向量训练RF模型,根据RF模型对未知样本的识别能力筛选特征,由此建立特征数据集。根据特征数据集建立RF模型,对200组测试集样本进行识别,准确率达96.5%。
(2) 从泛化能力和识别效率2个方面研究了RF模型的性能,结果表明当决策树数量设置为100或150时,RF模型的识别准确率最高,达97%,同时对测试集样本进行特征提取与识别的耗时不超过0.2 s。研究结果验证了本文方法可快速、准确地实现煤矸识别。
[1] 于斌,徐刚,黄志增,等.特厚煤层智能化综放开采理论与关键技术架构[J].煤炭学报,2019,44(1):42-53.
YU Bin,XU Gang,HUANG Zhizeng,et al.Theory and its key technology framework of intelligentized fully-mechanized caving mining in extremely thick coal seam[J].Journal of China Coal Society,2019,44(1):42-53.
[2] 张宁波,鲁岩,刘长友,等.综放开采煤矸自动识别基础研究[J].采矿与安全工程学报,2014,31(4):532-536.
ZHANG Ningbo,LU Yan,LIU Changyou,et al.Basic study on automatic detection of coal and gangue in the fully mechanized top coal caving mining[J].Journal of Mining & Safety Engineering,2014,31(4):532-536.
[3] 张宁波,刘长友,陈现辉,等.综放煤矸低水平自然射线的涨落规律及测量识别分析[J].煤炭学报,2015,40(5):988-993.
ZHANG Ningbo,LIU Changyou,CHEN Xianhui,et al.Measurement analysis on the fluctuation characteristics of low level natural radiation from gangue[J].Journal of China Coal Society,2015,40(5):988-993.
[4] 张守祥,张艳丽,王永强,等.综采工作面煤矸频谱特征[J].煤炭学报,2007,32(9):971-974.
ZHANG Shouxiang,ZHANG Yanli,WANG Yongqiang,et al.Caved coal and rock spectrum on longwall face[J].Journal of China Coal Society,2007,32(9):971-974.
[5] 薛光辉,赵新赢,柳二猛,等.基于振动信号时域特征的综放工作面煤岩识别[J].煤炭科学技术,2015,43(12):92-97.
XUE Guanghui,ZHAO Xinying,LIU Ermeng,et al.Time-domain characteristic extraction of coal and rock vibration signal in fully-mechanized top coal caving face[J].Coal Science and Technology,2015,43(12):92-97.
[6] 李一鸣,符世琛,李瑞,等.垮落煤岩性状识别研究[J].工矿自动化,2017,43(2):24-28.
LI Yiming,FU Shichen,LI Rui,et al.Reseaech on identification of caving coal and rock traits[J].Industry and Mine Automation,2017,43(2):24-28.
[7] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceeding of the Royal Society London A,1998,454(1971):903-995.
[8] HUANG N E.A new method for nonlinear and nonstationary time series analysis:empirical mode decomposition and Hilbert spectral analysis[J].Proceedings of the International Society for Optical Engineering,2000,4056:197-209.
[9] 林选,田慕琴.基于小波包和EMD的异步电动机轴承故障诊断方法[J].工矿自动化,2010,36(6):49-53.
LIN Xuan,TIAN Muqin.Fault diagnosis method of bearing of asynchronous motor based on wavelet-packet and EMD[J].Industry and Mine Automation,2010,36(6):49-53.
[10] 李康强,冯志鹏.基于EMD和能量算子的模态参数识别在行星齿轮箱中的应用[J].振动与冲击,2018,37(8):1-8.
LI Kangqiang,FENG Zhipeng.Modal parameter identification based on empirical mode decomposition and energy operator for planetary gearboxes[J].Journal of Vibration and Shock,2018,37(8):1-8.
[11] 付晓波.经验模态分解法理论研究与应用[D].太原:太原理工大学,2013.
FU Xiaobo.Research on empirical mode decomposition theory and its application[D].Taiyuan:Taiyuan University of Technology,2013.
[12] 方保镕,周继东,李医民.矩阵论[M].2版.北京:清华大学出版社,2013.
FANG Baorong,ZHOU Jidong,LI Yimin. Matrix theory[M].2nd Edition.Beijing:Tsinghua University Press,2013.
[13] 李梅.信息论基础与应用[M].北京:电子工业出版社,2016.
LI Mei.Foundation and application of information theory[M].Beijing:Publishing House of Electronics Industry,2016.
[14] HARTE J,NEWMAN E A.Maximum information entropy:a foundation for ecological theory[J].Trends in Ecology & Evolution,2014,29(7):384-389.
[15] 赵志宏,杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击,2012,31(6):136-140.
ZHAO Zhihong,YANG Shaopu.Sample entropy-based roller bearing fault diagnosis method[J].Journal of Vibration and Shock,2012,31(6):136-140.
[16] LIAW A,WIENER M.Classification and regression by random forest[J].R News,2002,2(3):18-22.
[17] 方匡南,吴见彬,朱建平,等.随机森林方法研究综述[J].统计与信息论坛,2011,26(3):32-38.
FANG Kuangnan,WU Jianbin,ZHU Jianping,et al.A review of technologies on random forests[J].Statistics & Information Forum,2011,26(3):32-38.
[18] 曹正凤.随机森林算法优化研究[D].北京:首都经济贸易大学,2014.
CAO Zhengfeng.Study on optimization of random forests algorithm[D].Beijing:Capital University of Economics and Business,2014.