0 引言
矿井提升机是矿井运输过程中的重要设备,矿井提升机的运行要求安全、可靠,停车位置准确。矿井提升机控制的实质是行程给定的情况下实现运行速度的控制。传统的矿井提升机采用梯形速度曲线进行行程控制,但不能实现提升机在加减速和启停车阶段速度的平滑过渡,极易在传动系统中产生大电流冲击,造成钢丝绳张力突变和设备故障,影响提升机的安全运行和使用寿命,且无法满足人体对乘坐舒适感的要求。目前我国矿井提升机多采用S形速度曲线进行行程控制,可满足提升机运行安全、可靠、高效、舒适等要求[1-4],然而提升机最大速度、加速度、急动度都是根据《煤矿安全规程》和专家经验给出固定值,导致提升机运行能耗较大[5-6]。本文提出了一种矿井提升机节能运行的行程控制方法,利用模拟退火-遗传算法求解矿井提升机能耗最小时的S形速度曲线参数,进而确定S形速度曲线来控制提升机行程,达到节能目的。
1 矿井提升机S形速度曲线
矿井提升机S形速度曲线如图1所示(v,a,r,t分别为提升机运行速度、加速度、急动度、时间)。在1个提升周期中,速度曲线分为初变加速段oa、等加速段ab、末变加速段bc、匀速段cd、初变减速段de、等减速段ef、末变减速段fg,其中减速段与加速段对称。
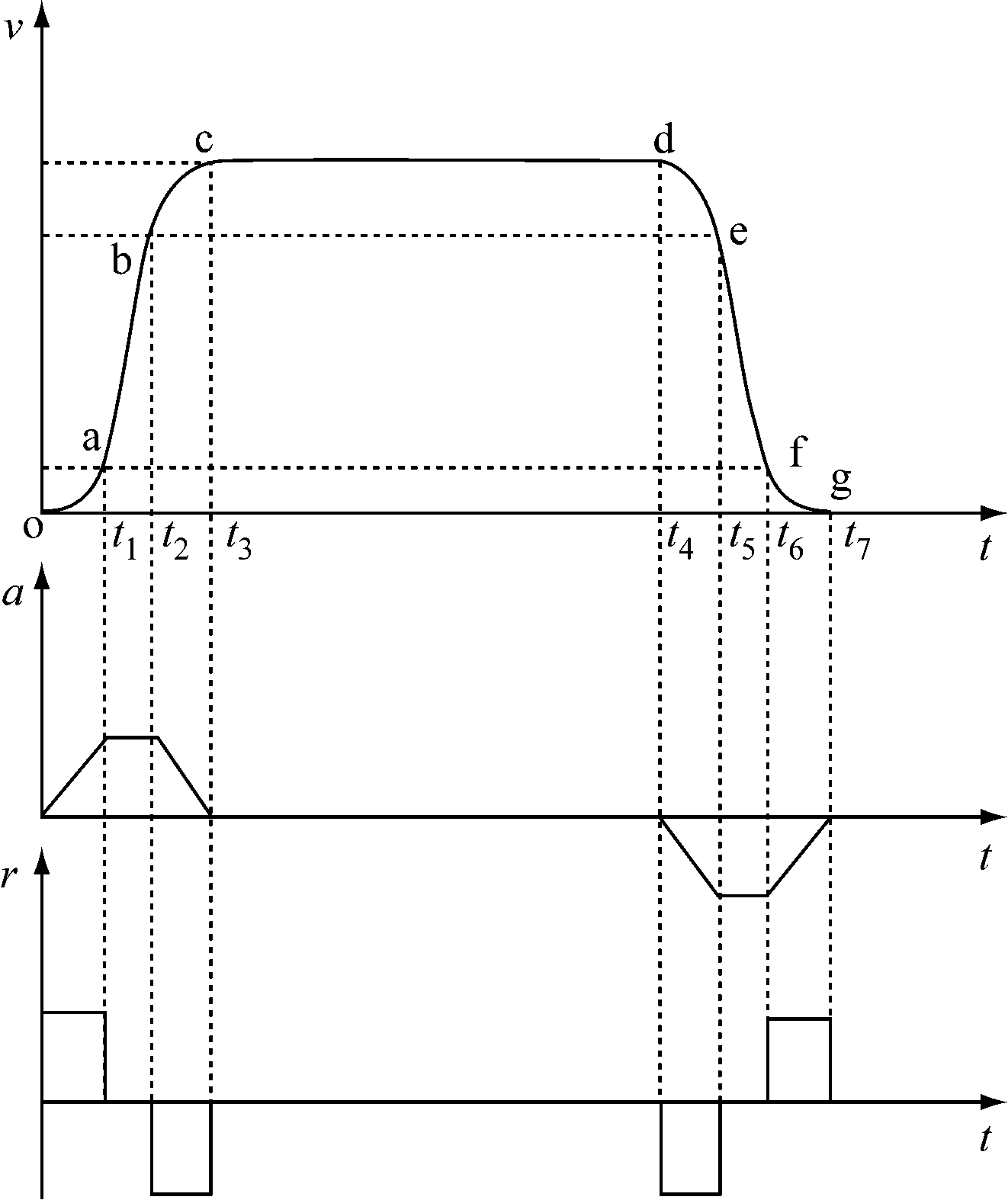
图1 矿井提升机S形速度曲线
Fig.1 S-shaped speed curve of mine hoist
在初变加速段oa(0≤t≤t1),提升机运行速度v1与行程s1为
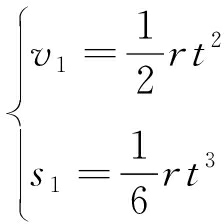
(1)
在等加速段ab(t1≤t≤t2),提升机运行速度v2与行程s2为
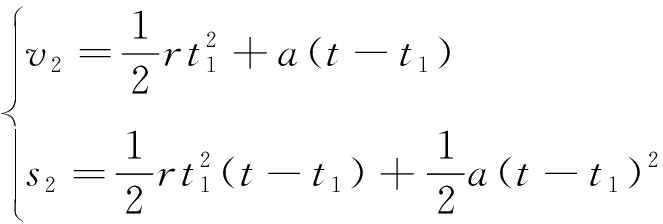
(2)
在末变加速段bc(t2≤t≤t3),提升机运行速度v3与行程s3为
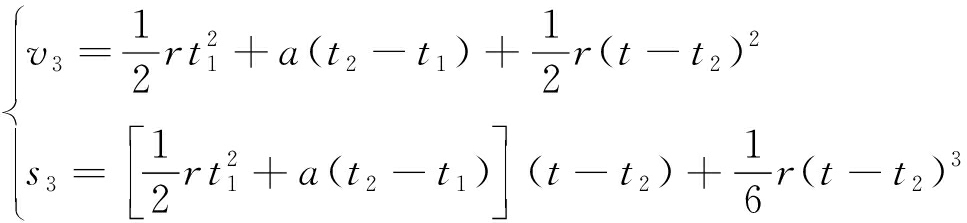
(3)
在匀速段cd(t3≤t≤t4),提升机运行速度v4与行程s4为
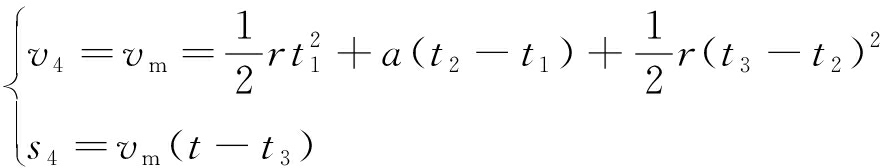
(4)
式中vm为提升机运行最大速度,m/s。
在初变减速段de(t4≤t≤t5),提升机运行速度v5与行程s5为
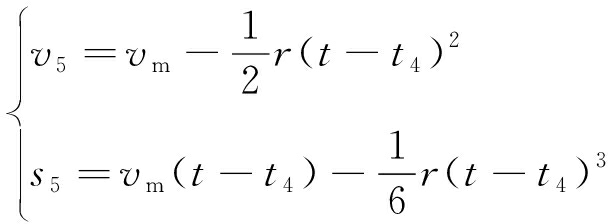
(5)
在等减速段ef(t5≤t≤t6),提升机运行速度v6与行程s6为
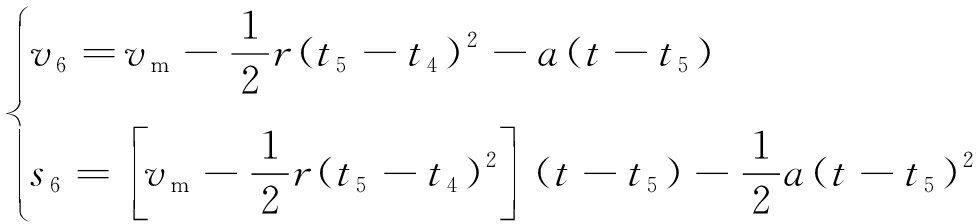
(6)
在末变减速段fg(t6≤t≤t7),提升机运行速度v7与行程s7为
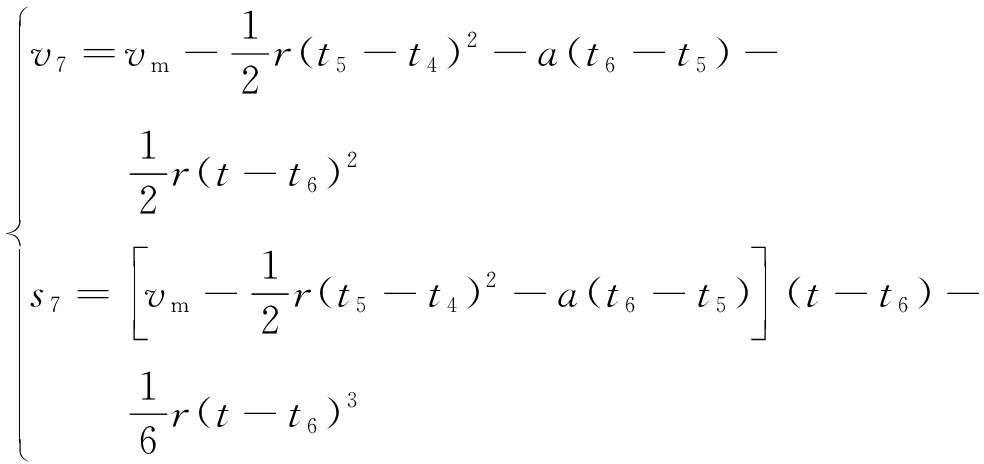
(7)
提升机总行程为
s=s1+s2+s3+s4+s5+s6+s7=H
(8)
式中H为提升机提升高度,m。
只要根据生产状况选择合适的加速度a、急动度r、最大速度vm,即可确定整个S形速度曲线,实现提升机行程控制。
2 矿井提升机能耗
由提升机动力学和电力学特性可知,提升机1次提升所消耗电能为
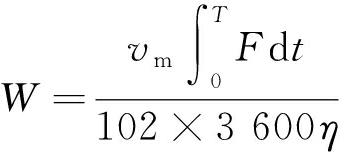
(9)
式中:T为1次提升周期,s;F为各阶段电动机拖动力,N;η为电能转换为机械能的效率。
由图1可得各阶段电动机拖动力总和为
![]() Fdt=(KQg+m r t)t1+(KQg+ma)(t2-t1)+
Fdt=(KQg+m r t)t1+(KQg+ma)(t2-t1)+
[KQg+m(a-r t)](t3-t2)+KQg(t4-t3)+
[KQg+m(-r t)](t5-t4)+(KQg-ma)(t6-
t5)+[KQg-m(a-r t)](t7-t6)
(10)
式中:K为矿井阻力系数,一般为1.15;Q为1次提升载荷,t;g为重力加速度,m/s2;m为变位质量,kg。
由图1曲线的对称性可知t1=t3-t2=t5-t4=t7-t6,t2-t1=t6-t5,则式(10)简化为
![]() Fdt=KQgt7=KQgT
Fdt=KQgt7=KQgT
(11)
由式(9)和式(11)可知,要求解W则应求解vm和T,而求解T需要已知S形速度曲线的t1—t7,参数众多,很难求出。
S形速度曲线是在梯形速度曲线(图2)的基础上改进而来,下面讨论在相同vm和T的情况下,梯形速度曲线控制下提升机1次提升能耗。
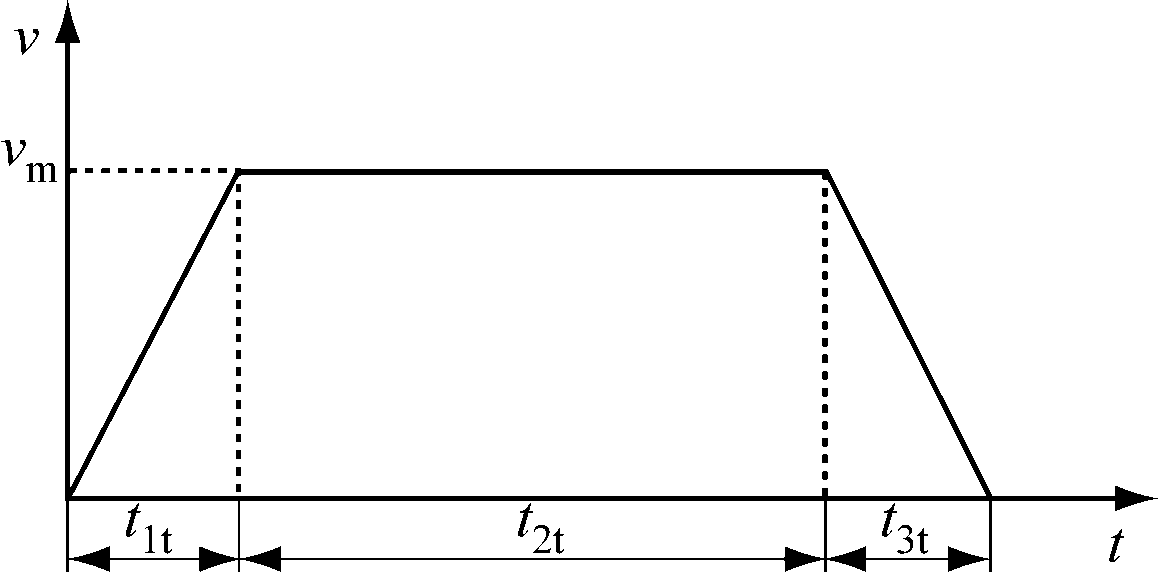
图2 矿井提升机梯形速度曲线
Fig.2 Trapezoidal speed curve of mine hoist
由图2可得各阶段电动机拖动力总和:
![]() Fdt=(KQg+ma)t1t+KQgt2t+(KQg-ma)t3t
Fdt=(KQg+ma)t1t+KQgt2t+(KQg-ma)t3t
(12)
式中t1t,t2t,t3t分别为加速段、匀速段和减速段提升机运行时间,s。
由图2曲线的对称性可知t1t=t3t,则式(12)简化为
![]() Fdt=KQgt1t+KQgt2t+KQgt3t=
Fdt=KQgt1t+KQgt2t+KQgt3t=
KQg(t1t+t2t+t3t)=KQgT
(13)
由式(9)、式(11)和式(13)可知,在相同的提升周期、最大速度下,分别采用S形速度曲线和梯形速度曲线控制提升机行程产生的1次提升能耗相同。图2相关参数简单,因此下面以梯形速度曲线代替S形速度曲线来分析提升机1次提升能耗。
根据运动学关系,可得图2中相关参数:
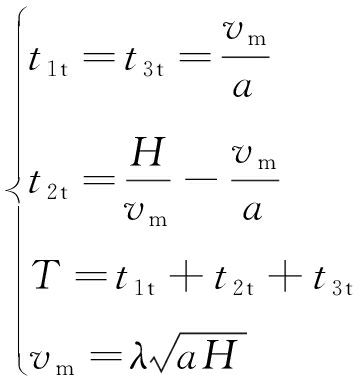
(14)
式中λ为提升机运行速度权重,λ∈(0,1)。
进而可得
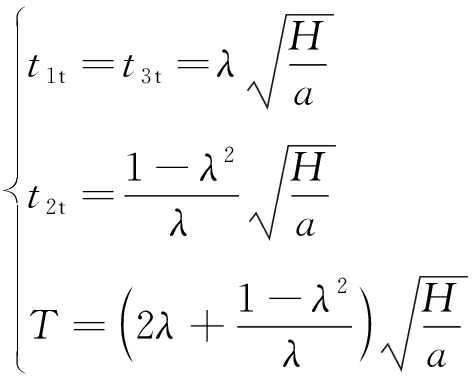
(15)
则1次提升载荷为
![]()
(16)
式中:A为工作面每小时产量,t/h;tr为1个提升周期中提升机停歇时间,s。
将式(15)、式(16)代入式(13),可得
![]()
(17)
则式(9)转换为
![]()
(18)
在式(18)中,A,tr,K,H,g,η均为提升机的固定参数,因此提升机1次提升能耗W主要由提升机运行速度权重λ和提升机运行加速度a决定。
3 矿井提升机节能运行的行程控制参数求解
由于式(18)中有λ和a 2个变量,无法用普通数学求极值的方法求出能耗W的最小值。遗传算法使用群体搜索技术,有较强的全局搜索能力,但容易出现“早熟”现象,陷入局部最优解[7-9]。模拟退火算法具有很强的局部搜索能力,但对全局的掌握情况不够,且寻优较慢,搜索效率不高[10-12]。鉴于此,本文利用模拟退火-遗传算法求解能耗最小时的λ和a,从而得到提升机运行最大速度vm和1次提升周期T,进而可得急动度r和提升机各阶段运行时间。
基于模拟退火-遗传算法的矿井提升机行程控制参数求解流程如图3所示。首先,初始化种群,计算初始种群中各个体的适应度值并将其作为模拟退火算法中的初始解;然后,遗传算法通过选择、交叉和变异产生新种群,计算新种群中各个体的适应度值并将其作为模拟退火算法中的新解;最后,将模拟退火算法的新解通过Metropolis规则替换初始解[13-15]。
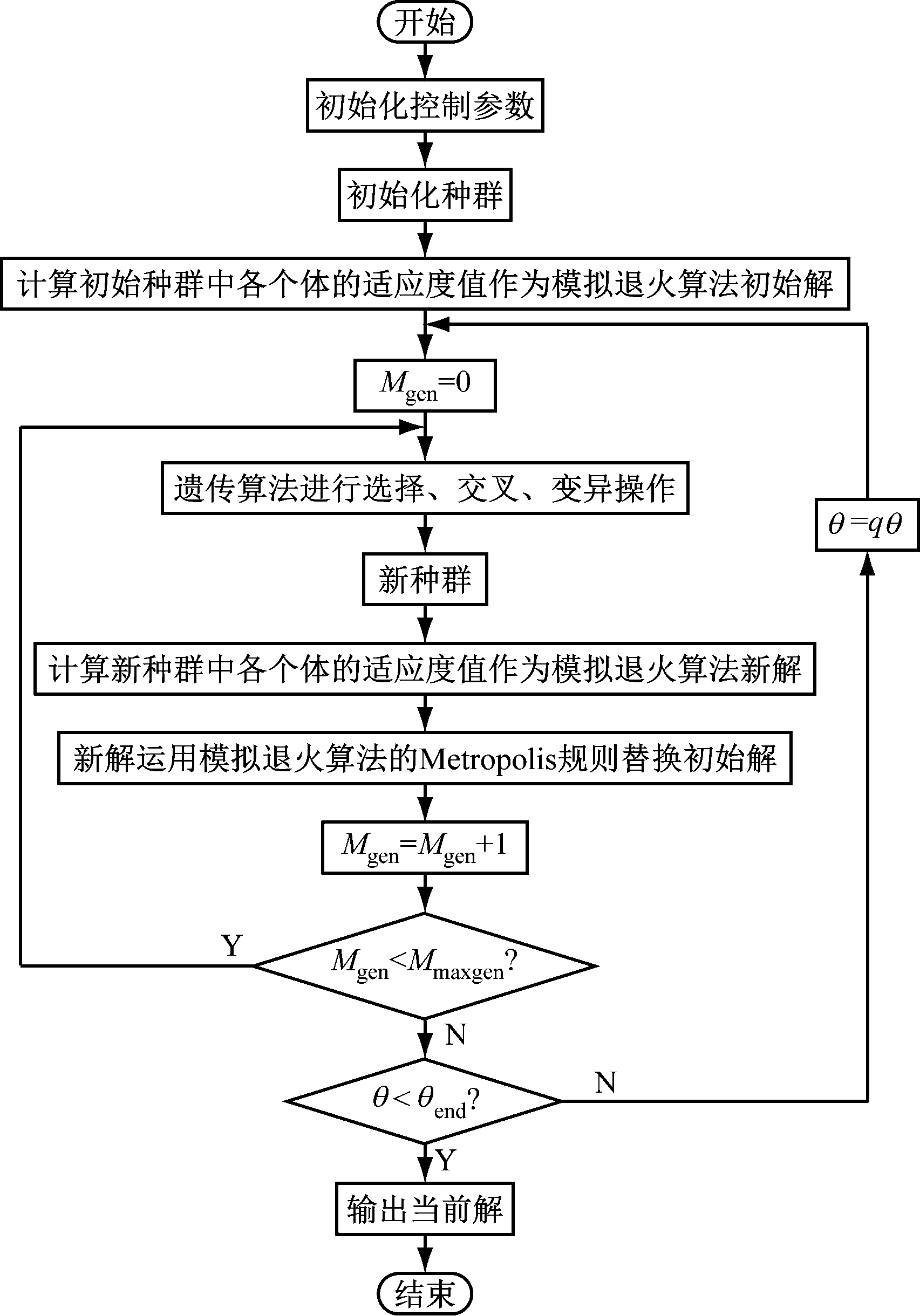
图3 基于模拟退火-遗传算法的矿井
提升机行程控制参数求解流程
Fig.3 Flow of mine hoist stroke control parameters solution based on simulated annealing-genetic algorithm
模拟退火-遗传算法对优化问题求解过程中,考察个体的唯一指标就是适应度值,因此适应度函数的建立尤为重要。根据式(18)建立适应度函数:
![]()
![]()
(19)
基于模拟退火-遗传算法的提升机行程控制参数求解实现步骤如下。
Step1 初始化参数,包括种群规模N、最大进化次数Mmaxgen、交叉概率px、变异概率pm、初始温度θ0、温度冷却系数q、终止温度θend。
Step2 随机生成初始种群,利用式(19)计算每个个体的适应度值Ji,i=1,2,…,N。
Step3 设循环计数变量Mgen=0。
Step4 对初始种群实施选择、交叉和变异等遗传操作,进化得到新种群,对新产生的个体用式(19)计算适应度值![]()
Step5 计算退火增量![]() 若ΔJ<0,则以新个体替换旧个体;否则,以概率P=
若ΔJ<0,则以新个体替换旧个体;否则,以概率P=![]() (θ为当前温度)接受新个体,舍弃旧个体。
(θ为当前温度)接受新个体,舍弃旧个体。
Step6 令Mgen=Mgen+1。若Mgen<Mmaxgen,则转至Step4;否则,转至Step7。
Step7 若θ<θend,则输出最小适应度值对应的全局最优当前解;否则,执行降温操作θ=qθ,转至Step3。
4 仿真结果与分析
针对模拟退火-遗传算法,利用Matlab 2016a软件平台进行仿真。参数设置:H=516.5 m,tr=18 s,a=0.6~0.8 m/s2,N=40,Mmaxgen=200,px=0.7,pm=0.01,θ0=100 ℃,q=0.8,θend=1 ℃。通过仿真得到适应度函数进化过程及其分布,分别如图4和图5所示。
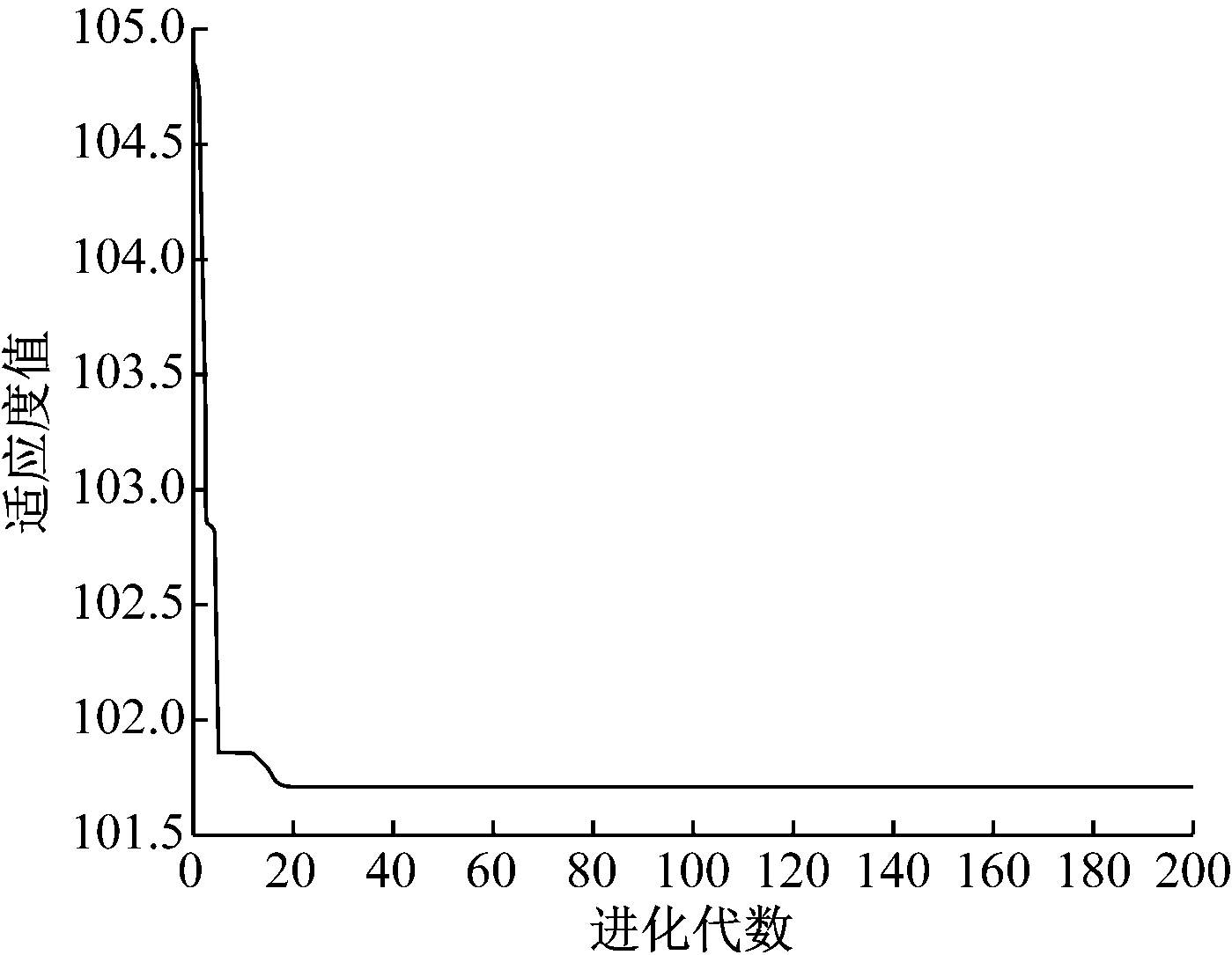
图4 适应度函数进化过程
Fig.4 Evolutionary process of fitness function
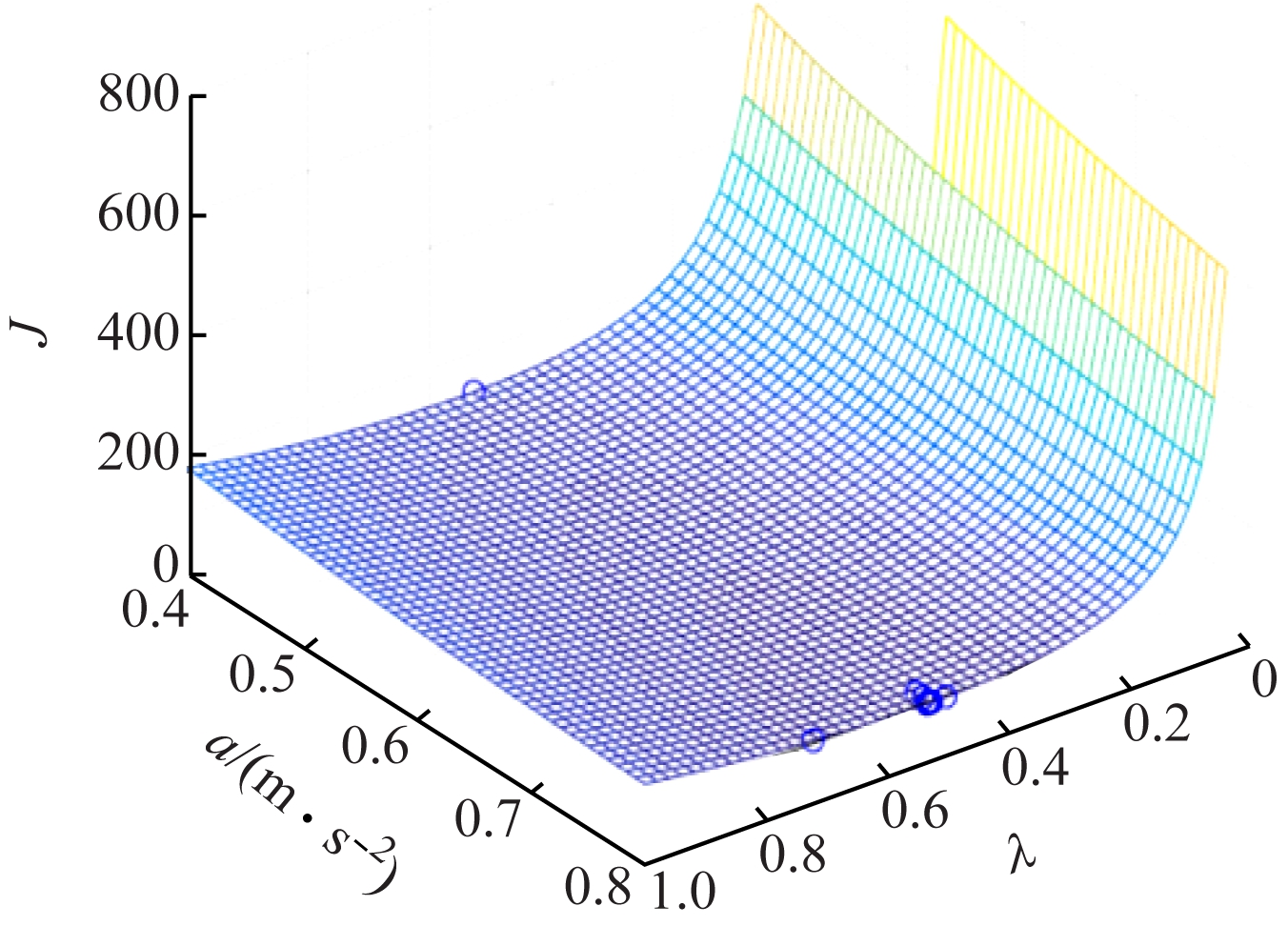
图5 适应度函数分布
Fig.5 Distribution of fitness function
由图4可知,模拟退火-遗传算法在经过20代进化后寻找到全局最优解,运行效率较高,能快速收敛至最优解。由图5可知,模拟退火-遗传算法寻优结果为λ=0.528 14,a=0.8 m/s2,J=101.713 7。由此可得其他提升机行程控制参数优化值:提升机运行最大速度vm=10.735 7 m/s,提升机运行周期T=61.530 2 s,急动度r=0.75 m/s3。
某矿井提升机行程控制参数的实际值与优化值对比见表1。可看出优化后提升机1次提升能耗降低了9.14%,表明本文方法具有较好的节能效果。
表1 矿井提升机行程控制参数实际值与优化值
Table 1 Actual value and optimal value of a mine hoist stroke control parameters
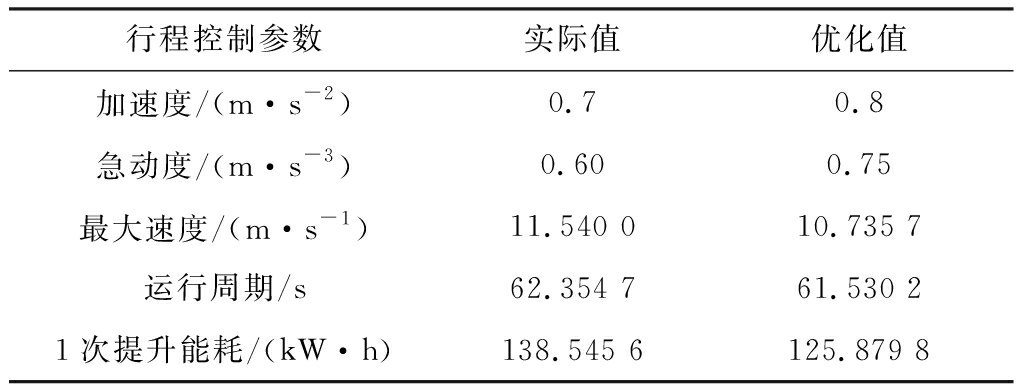
行程控制参数实际值优化值加速度/(m·s-2)0.70.8急动度/(m·s-3)0.600.75最大速度/(m·s-1)11.540 010.735 7运行周期/s62.354 761.530 21次提升能耗/(kW·h)138.545 6125.879 8
5 结论
(1) 在提升机运行最大速度和提升周期相同的情况下,分别采用梯形速度曲线和S形速度曲线控制提升机行程时产生的1次提升能耗相同,进而给出了矿井提升机1次提升能耗关于提升机运行速度权重和加速度的表达式。
(2) 利用模拟退火-遗传算法求解提升机1次提升能耗最小时的提升机运行速度权重和加速度,进而确定提升机运行最大速度、提升周期、急动度等提升机S形速度曲线参数,从而采用该确定的S形速度曲线控制提升机行程,可降低能耗9.14%,具有较好的节能效果。
[1] 苏长胜.矿井提升机控制技术研究现状与发展[J].工矿自动化,2013,39(2):33-38.
SU Changsheng.Research status and development of control technology for mine hoist[J].Industry and Mine Automation,2013,39(2):33-38.
[2] 范子荣.矿井提升机的控制方法研究[J].计算机仿真,2015,32(8):364-368.
FAN Zirong.Study on control method of mine hoist[J].Computer Simulation,2015,32(8):364-368.
[3] 杨军坤,王聪,王安山,等.矿井提升机行程控制的研究及设计[J].煤炭工程,2013,45(5):11-13.
YANG Junkun,WANG Cong,WANG Anshan,et al.Research and design of travel control of mine hoist[J].Coal Engineering,2013,45(5):11-13.
[4] 刘豫喜,刘建英.提升机的速度和位置控制算法[J].煤矿机械,2014,35(5):37-38.
LIU Yuxi,LIU Jianying.Algorithm of control speed and position of hoister[J].Coal Mine Machinery,2014,35(5):37-38.
[5] 李志海.煤矿主要耗能设备经济运行分析及节能整改措施研究[J].能源与环保,2020,42(2):71-74.
LI Zhihai.Analysis on economic operation of main energy consuming equipment in coal mine and study on energy saving rectification measures[J].China Energy and Environmental Protection,2020,42(2):71-74.
[6] 祝坚,李玉瑾,张保连.矿井提升系统经济运行特性分析[J].煤炭工程,2014,46(7):22-23.
ZHU Jian,LI Yujin,ZHANG Baolian.Analysis on economic operation features of mine shaft hoisting system[J].Coal Engineering,2014,46(7):22-23.
[7] 刘丹丹,刘衡,李德文,等.基于遗传算法的煤矿粉尘浓度测量装置优化[J].黑龙江科技大学学报,2018,28(1):97-101.
LIU Dandan,LIU Heng,LI Dewen,et al.Optimization research on coal dust concentration measurement device based on genetic algorithm[J].Journal of Heilongjiang University of Science and Technology,2018,28(1):97-101.
[8] XU Mingji,LI Sheng,GUO Jian.Optimization of multiple traveling salesman problem based on simulated annealing genetic algorithm[J].MATEC Web of Conferences,2017,100(5):2025-2032.
[9] 张维,杨康宁,张民.一种求解不等圆Packing问题的改进遗传模拟退火算法[J].西北工业大学学报,2017,35(6):1033-1039.
ZHANG Wei,YANG Kangning,ZHANG Min.An improved genetic simulated annealing algorithm to solve the unequal circle Packing problem[J].Journal of Northwestern Polytechnical University,2017,35(6):1033-1039.
[10] 李建国,贺云鹏,常立丹.基于改进模拟退火算法的立体车库车位分配优化[J].重庆理工大学学报(自然科学版),2020,34(4):183-191.
LI Jianguo,HE Yunpeng,CHANG Lidan.Optimization of stereo parking allocation based on improved simulated annealing algorithm[J].Journal of Chongqing University of Technology(Natural Science),2020,34(4):183-191.
[11] 蔡金祥,蔡金涛,袁建华,等.基于混合遗传算法与模拟退火算法的金属氧化物避雷器在线监测研究[J].电力学报,2019,34(3):261-267.
CAI Jinxiang,CAI Jintao,YUAN Jianhua,et al.Online monitoring of metal oxide arrester aging based on hybrid genetic algorithm and simulated annealing algorithm[J].Journal of Electric Power,2019,34(3):261-267.
[12] 王亚楠,康英伟,郑鹏远,等.基于遗传模拟退火算法的最大功率点跟踪研究[J].上海电力学院学报,2016,32(3):252-256.
WANG Yanan,KANG Yingwei,ZHENG Pengyuan,et al.Research of maximum power point tracking based on genetic simulated annealing algorithm[J].Journal of Shanghai University of Electric Power,2016,32(3):252-256.
[13] ZHANG Tengfei,GUO Jikun,YAN Qiaoqiao.Optimization of hazardous POL transportation problem based on simulated annealing genetic algorithm[J].Chemical Engineering Transactions,2018,66:1471-1476.
[14] 曹现刚,宫钰蓉,雷一楠.基于模拟退火遗传算法的自动化立体仓库货位优化[J].机床与液压,2020,48(14):67-72.
CAO Xiangang,GONG Yurong,LEI Yinan.Optimization of automatic storage location based on simulated annealing genetic algorithm[J].Machine Tool and Hydraulics,2020,48(14):67-72.
[15] 高天阳,虞慧群,范贵生.基于模拟退火遗传算法的云资源调度方法[J].华东理工大学学报(自然科学版),2019,45(3):471-477.
GAO Tianyang,YU Huiqun,FAN Guisheng.Simulated annealing genetic algorithm based approach to cloud resource scheduling[J].Journal of East China University of Science and Technology,2019,45(3):471-477.