0 引言
随着5G技术在世界范围内逐渐商用,矿山开采过程逐渐趋向无人/少人化,在采煤和掘进等工作面均存在海量大型机械设备和智能装备机器人,通过其动态协同作业实现井下数据高效连续传输[1-2]。采煤机、带式输送机等机械设备撞击、摩擦等产生的机械噪声,以及磁场脉动、电源频率脉动等引起的电磁噪声,会对工业无线通信系统产生严重影响[3]。与传统的加性高斯白噪声相比,工业噪声是随机产生的,脉冲持续时间较短,脉冲功率和高功率谱密度较高,因此可用脉冲噪声模型来描述。工业噪声会导致通信系统的突发数据错误,显著降低数据传输可靠性和通信质量,已成为实现高速、可靠工业无线通信系统的瓶颈。
正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术因其数据速率高的特点被广泛应用于各种工业无线通信场景。与单载波系统相比,OFDM系统对多径衰落和脉冲噪声的影响有一定的鲁棒性,但是当脉冲噪声能量过高时,其通过快速傅里叶变换(Fast Fourier Transform, FFT)解调过程扩散至所有子信道上,从而导致工业无线通信性能严重下降[4-5]。文献[6]研究了脉冲噪声和高斯噪声下的系统和速率。文献[7-8]分析了具有脉冲干扰的多输入多输出(Multiple-Input Multiple-Output, MIMO)-OFDM工业无线通信的系统和速率。上述文献仅分析了不同脉冲噪声环境下的香农极限。文献[9]比较了5G工业无线通信系统不同预编码设计方案的性能。文献[10]设计了一种考虑脉冲噪声影响的低复杂度MIMO-OFDM系统线性预编码方案。文献[11]提出了一种预编码设计方案,以最大化电力线MIMO-OFDM通信系统和速率。然而,目前关于工业脉冲噪声环境下的预编码设计方案仍然很少。
由于脉冲噪声在工业场景中的普遍性及其对OFDM系统的影响,抗脉冲噪声的接收机设计是工业无线通信的一个研究热点。现存的接收机脉冲噪声消除方案主要分为2类:第1类利用了脉冲噪声的稀疏性和OFDM信号的结构,脉冲噪声的估计由空子载波或导频子载波推断出,然后从接收到的信号中减去估计的脉冲噪声[12-15]。这类方案对OFDM系统的设计要求很高,不适用于工业无线通信系统。第2类是目前主流的非线性脉冲噪声消除方案,主要包括消隐、削减和混合3种[4]。这类方案复杂度较低且具有较好的噪声消除效果。此外,文献[11]和文献[16]提出在发射端设计峰均比抑制方案,在接收端设计非线性脉冲噪声消除方案,以减小系统误码率(System Error Rate, SER)。现有的抗脉冲噪声研究大多只能保证通信系统的有效性或可靠性。而工业无线通信场景中的任务应用对有效性和可靠性都提出了较高要求,单一的性能研究无法满足需求。针对以上问题,综合考虑工业设备尺寸和设计复杂性,本文提出一种联合收发端设计的多用户多输入单输出(Multi-User Multiple-Input Single-Output, MU-MISO)-OFDM系统模型。在此基础上,设计满足机器型通信设备(Machine-Type Communication Devices, MTCDs)服务质量的预编码算法,以最大化系统和速率,同时为进一步提高工业无线通信的可靠性,设计了脉冲噪声消除方案。
1 系统模型
考虑一个典型的MU-MISO-OFDM下行工业无线通信系统,该系统包含1个装备M根天线的基站和N个单天线的机器型通信设备,用N={1,2,…,N}表示MTCDs集合,用hn∈![]() M×1(M×1的矢量)和wn∈
M×1(M×1的矢量)和wn∈![]() M×1表示第n个MTCD的信道增益矢量和预编码矢量。联合收发端设计OFDM接收机,以保障工业无线通信的系统和速率及可靠性。第n个MTCD的OFDM收发机设计如图1所示,其中IFFT表示快速傅里叶逆变换,sn为经过预编码设计和信道衰落后的信号,yn为经深度削减降噪处理的信号。在发射端设计预编码方案,在接收端设计深度削减脉冲噪声消除模块。第n个MTCD的接收信号rn可表示为
M×1表示第n个MTCD的信道增益矢量和预编码矢量。联合收发端设计OFDM接收机,以保障工业无线通信的系统和速率及可靠性。第n个MTCD的OFDM收发机设计如图1所示,其中IFFT表示快速傅里叶逆变换,sn为经过预编码设计和信道衰落后的信号,yn为经深度削减降噪处理的信号。在发射端设计预编码方案,在接收端设计深度削减脉冲噪声消除模块。第n个MTCD的接收信号rn可表示为
(1)
式中:xn为第n个MTCD从基站接收到的信号矢量,其归一化功率![]() 表示期望值;zn为包含脉冲噪声和背景噪声的噪声信号矢量。
表示期望值;zn为包含脉冲噪声和背景噪声的噪声信号矢量。

图1 OFDM收发机设计
Fig.1 OFDM transceiver design
为研究脉冲噪声对工业无线通信的影响,背景噪声zg通常被建模成均值为0、方差为![]() 的加性高斯白噪声。考虑工业噪声的特性,本文采用米德尔顿A类(Middleton Class A,MCA)脉冲噪声模型[17]对带式输送机、起重机、电力电缆等大型机械设备启动和运行引起的脉冲噪声zi进行建模,其概率密度函数(Probability Density Function,PDF)为
的加性高斯白噪声。考虑工业噪声的特性,本文采用米德尔顿A类(Middleton Class A,MCA)脉冲噪声模型[17]对带式输送机、起重机、电力电缆等大型机械设备启动和运行引起的脉冲噪声zi进行建模,其概率密度函数(Probability Density Function,PDF)为
(2)
式中:λ表示噪声状态;Φ为总的状态数;pλ为λ状态下的脉冲噪声发生概率,pλ=Ωλe-Ω/λ!,Ω为脉冲噪声指数,描述噪声的脉冲性,![]() 表示均值为0、方差为
表示均值为0、方差为![]() 的高斯PDF。
的高斯PDF。
式(2)表明,MCA模型假定不同干扰源产生的脉冲噪声在时间上服从Poisson分布,且
(3)
式中:![]() 为脉冲噪声功率;Γ为加性高斯白噪声功率
为脉冲噪声功率;Γ为加性高斯白噪声功率![]() 与脉冲噪声功率
与脉冲噪声功率![]() 的比值,
的比值,![]()
利用高斯伯努利分布模拟工业无线通信系统噪声分布:
zλ=bλzi,λ+zg
(4)
式中:zλ,zi,λ分别表示λ状态下的总噪声信号和脉冲噪声信号;bλ为脉冲噪声发生的频率,服从伯努利分布。
2 和速率最大化预编码算法
针对工业无线通信场景中的任务应用对系统和速率的要求,在发射端采用预编码设计来实现信道解耦,从而提高工业无线通信系统和速率。考虑到不同状态下的预编码设计不同,设λ状态下的第n个MTCD的预编码矢量为wn,λ∈![]() M×1,则接收信号为
M×1,则接收信号为
(5)
假定发射端和接收端都获取了所有设备的信道状态信息,且干扰链路服从瑞利衰落。用Rn,λ表示λ状态下的第n个MTCD的系统和速率,则由香农定理可得
Rn,λ=log2(1+γn,λ)
(6)
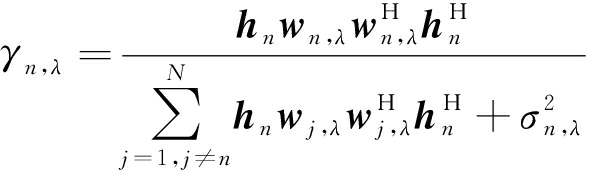
(7)
式中:γn,λ为信干噪比;![]() 为λ状态下的总噪声功率。
为λ状态下的总噪声功率。
考虑到脉冲噪声能量过高会导致信干噪比骤降,从而无法保证MTCDs服务质量并满足工业无线通信中机械设备的功率限制条件,最大化系统和速率的优化问题可描述为
s.t. γn,λ≥γn,min,∀n∈N
(8)
式中:γn,min为最小信干噪比;Pmax为最大发射功率。
式(8)中,第1个限制条件用于满足用户服务质量(Quality of Service, QoS)要求,第2个限制条件用于限制MTCDs的功率。
L1是非凸问题,γn,λ的分子和分母中预编码矢量耦合,导致该问题难以求解。针对该问题,本文提出一种基于二次型转换的算法[18],以较低的复杂度来求解优化问题。
为使优化目标便于处理,先引入任意非负变量tλ=[t1,λ,t2,λ,…,tN,λ],将其转换为凸函数,并将式(8)转换为
(9)
将式(8)的第1个限制条件处理为
γn,λ≥tn,λ,∀n∈N
(10)
tn,λ≥γn,min,∀n∈N
(11)
优化目标和约束条件式(11)均是凸的,下面利用二次型转换来处理非凸约束条件式(10),引入任意非负变量Yλ=[Y1,λ,Y2,λ,…,YN,λ],将式(10)转换为一系列凸约束:
(12)
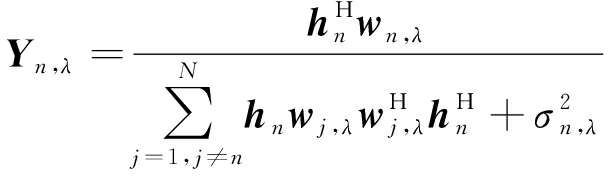
(13)
式中Re()表示取实部。
综合以上分析,优化问题L1可等效为
tn,λ≥γn,min,∀n∈N
(14)
当Yλ的值固定时,L2是一个标准凸优化问题,可采用标准凸优化工具及迭代算法来求解。具体算法如下。
基于二次型转换的预编码设计算法
1 迭代次数i=1,初始化变量![]() 和
和![]()
2 对每个状态λ,重复下述迭代过程;
3 按照式(13)更新![]()
4 用凸优化求解L2,得到最优解;
5 更新迭代次数,令![]() 为最优解;
为最优解;
6 直至目标函数收敛。
平均系统和速率为
(15)
3 深度削减脉冲噪声消除方案
考虑一个具有K个子载波的OFDM传输系统。在发射端,输入信号通过十六进制正交振幅调制(16-ary Quadrature Amplitude Modulation, 16-QAM)映射为基带符号,然后通过一个OFDM调制器,其时域信号s(τ)为
(16)
式中:τ为时间;Sk为输入的QAM符号;τ0为OFDM符号的时间间隔。
当脉冲噪声能量过高时,为缓解其对数据传输可靠性的影响,在接收端的传统OFDM 解调器前面增加深度削减脉冲噪声消除模块(图2),用于处理经过预编码设计的信号,从而缓解脉冲噪声导致SER增加的情况。该模块根据接收信号的幅值分3种情况进行处理。为便于分析,用3个互斥事件D0,D1,D2来描述接收信号rn。D0表示接收信号的幅值为0~T(T为削减门限阈值),若D0发生,则将接收到的信号视为发送信号,不受脉冲噪声的影响;D1表示接收信号的幅值为T~βT(β=(1+μ)/μ,μ为深度削减因子),若D1发生,则对接收信号幅值进行线性削减并加上相位补偿因子;D2表示接收信号的幅值大于βT,若D2发生,则认为接收信号为脉冲噪声,将其振幅设为0。经过深度削减降噪处理的信号为
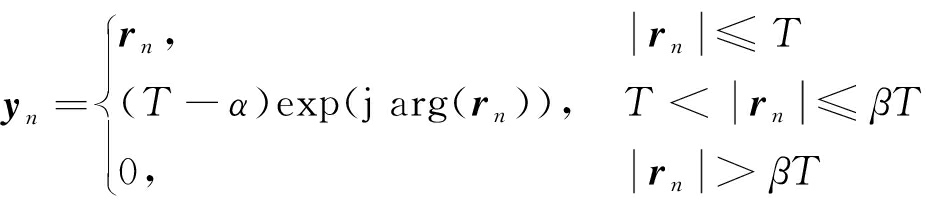
(17)
式中α=μ(|rn|-T)。
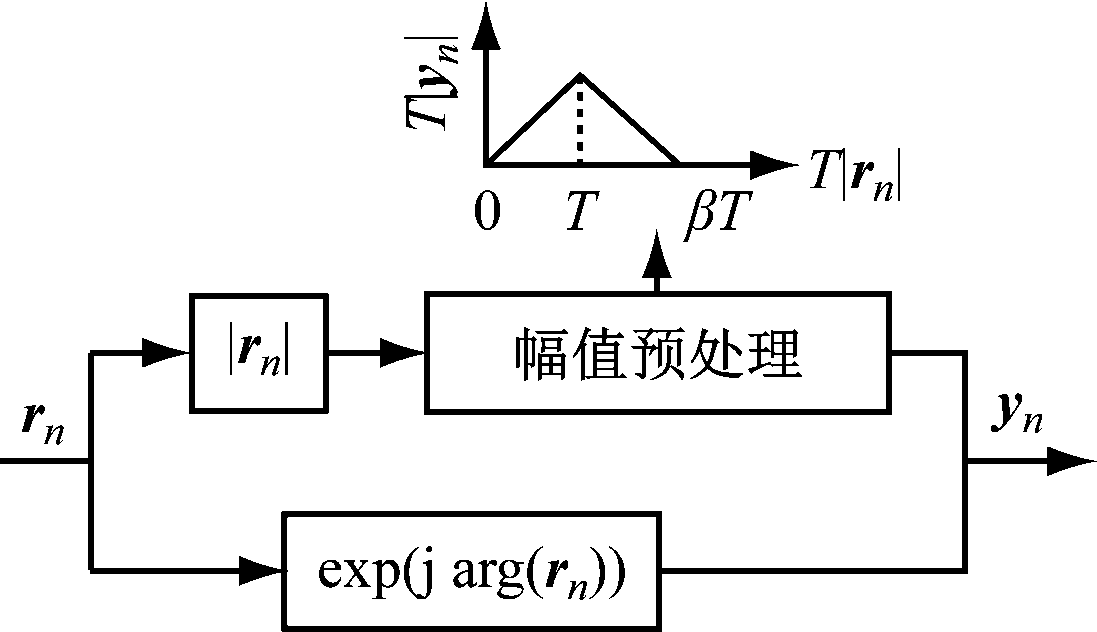
图2 深度削减脉冲噪声消除模块
Fig.2 Deep reduction impulsive noise limination module
经噪声消除处理的输出信号也可表示为
yn=Λsn+zn
(18)
(19)
式中:Λ为比例因子;![]() 为sn的共轭信号。
为sn的共轭信号。
根据文献[4],脉冲噪声经处理后的输出信噪比(Signal-to-Noise Ratio, SNR)为
(20)
当OFDM的子载波足够多时,OFDM信号可建模为Rayleigh包络分布的高斯过程,即输入信号xn服从参数为![]() 的Rayleigh分布,因此sn服从参数为
的Rayleigh分布,因此sn服从参数为![]() 的Rayleigh分布,则
的Rayleigh分布,则
(21)
对于深度削减脉冲噪声消除方案,E[![]() ]可表示为
]可表示为
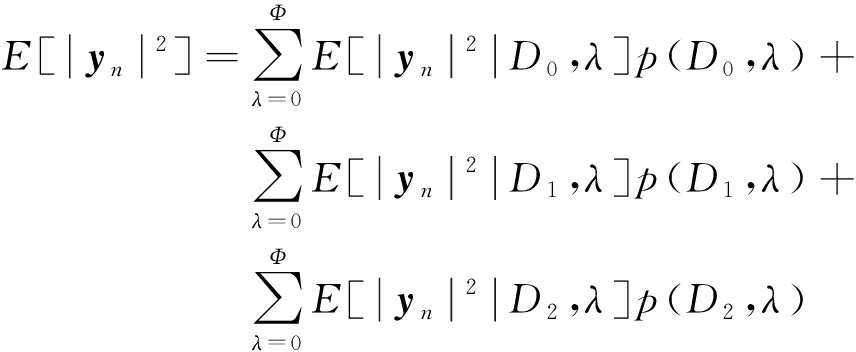
(22)
式中p(D0,λ),p(D1,λ),p(D2,λ)分别为事件D0-D2的联合发生概率。
由式(17)可得,E[![]() |D2,λ]=0。本文采用MCA脉冲噪声模型,则λ状态下接收信号的总方差为
|D2,λ]=0。本文采用MCA脉冲噪声模型,则λ状态下接收信号的总方差为![]() 事件D0和事件D1的联合发生概率分别为
事件D0和事件D1的联合发生概率分别为
p(D0,λ)=p(D0|λ)pλ=(1-A)pλ
(23)
p(D1,λ)=p(D1|λ)pλ=(A-B)pλ
(24)
式中:p(D0|λ),p(D1|λ)为条件概率;![]()
根据贝叶斯理论可得
(25)
(26)
根据文献[4]可得
(27)
式中![]() 表示高斯Q函数。
表示高斯Q函数。
将式(23)—式(25)、式(27)代入式(22),得到![]()
(28)
为求输出SNR,还需得到![]() 存在3个互斥事件D0,D1,D2,因此
存在3个互斥事件D0,D1,D2,因此![]() 可表示为
可表示为
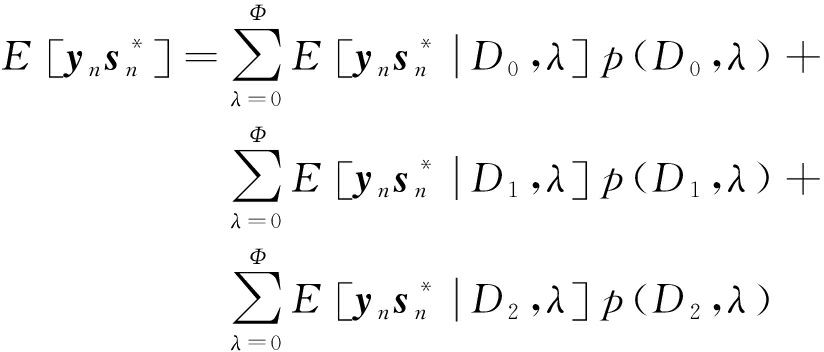
(29)
与式(22)同理,式(29)中的第3项为0,则![]() 为
为
(30)
![]() 难以直接推断,故本文推导
难以直接推断,故本文推导![]() 根据文献[19]可得
根据文献[19]可得
(31)
将式(23)、式(24)、式(30)、式(31)代入式(29),得到![]()
(32)
将式(21)和式(32)代入式(19)可得
(33)
OFDM系统的SER可表示为
(34)
式中θ为星座相位调制因子。
将式(21)、式(28)、式(33)代入式(20),可得到深度削减后的输出SNR。
4 仿真分析
通过Matlab对系统性能进行评估。为简化分析,假设链路的信道增益服从瑞利衰落。采用十六进制16-QAM对OFDM系统进行调制,子载波数为256。主要仿真参数如下:发射端天线数为4,MICD个数为4,脉冲噪声指数为0.01,加性高斯白噪声功率![]() 加性高斯白噪声功率与脉冲噪声功率的比值Γ=0.01,最大发射功率Pmax=15 dB。
加性高斯白噪声功率与脉冲噪声功率的比值Γ=0.01,最大发射功率Pmax=15 dB。
首先,以文献[20]提出的半正定松弛(Semi-Definite Relaxation, SDR)算法为基准,评估本文所提预编码算法的性能;然后,通过与主流的3种基准算法进行对比分析,评估所提的深度削减噪声消除方案的性能。第1种基准算法是文献[4]中的消隐算法,第2种算法是文献[5]中的削减算法,第3种算法是文献[11]中的非线性混合噪声消除算法。
4.1 预编码算法性能验证
选取4种噪声状态和高斯脉冲噪声状态,本文所提的基于二次型转换的预编码算法在不同状态下的系统和速率如图3所示。可以明显看出,高斯噪声环境下的系统和速率最大,这是因为脉冲噪声能量较高,会降低SNR,从而影响系统和速率。在4种脉冲噪声状态中,当噪声状态为0时,系统的系统和速率最大,且随着噪声状态数增大,系统和速率减小。原因是随着状态数的增加,对应状态数所出现的脉冲噪声功率增大,从而造成对应状态的系统和速率急剧下降。噪声状态数大于3时的和速率很小,为考虑仿真的复杂度,本文忽略更大的噪声状态数。与高斯脉冲噪声下的系统和速率相比,SNR为25 dB时,噪声状态为0时的系统和速率比高斯脉冲噪声下低3 bit/(s·Hz),验证了脉冲噪声对工业无线通信系统和速率的影响。
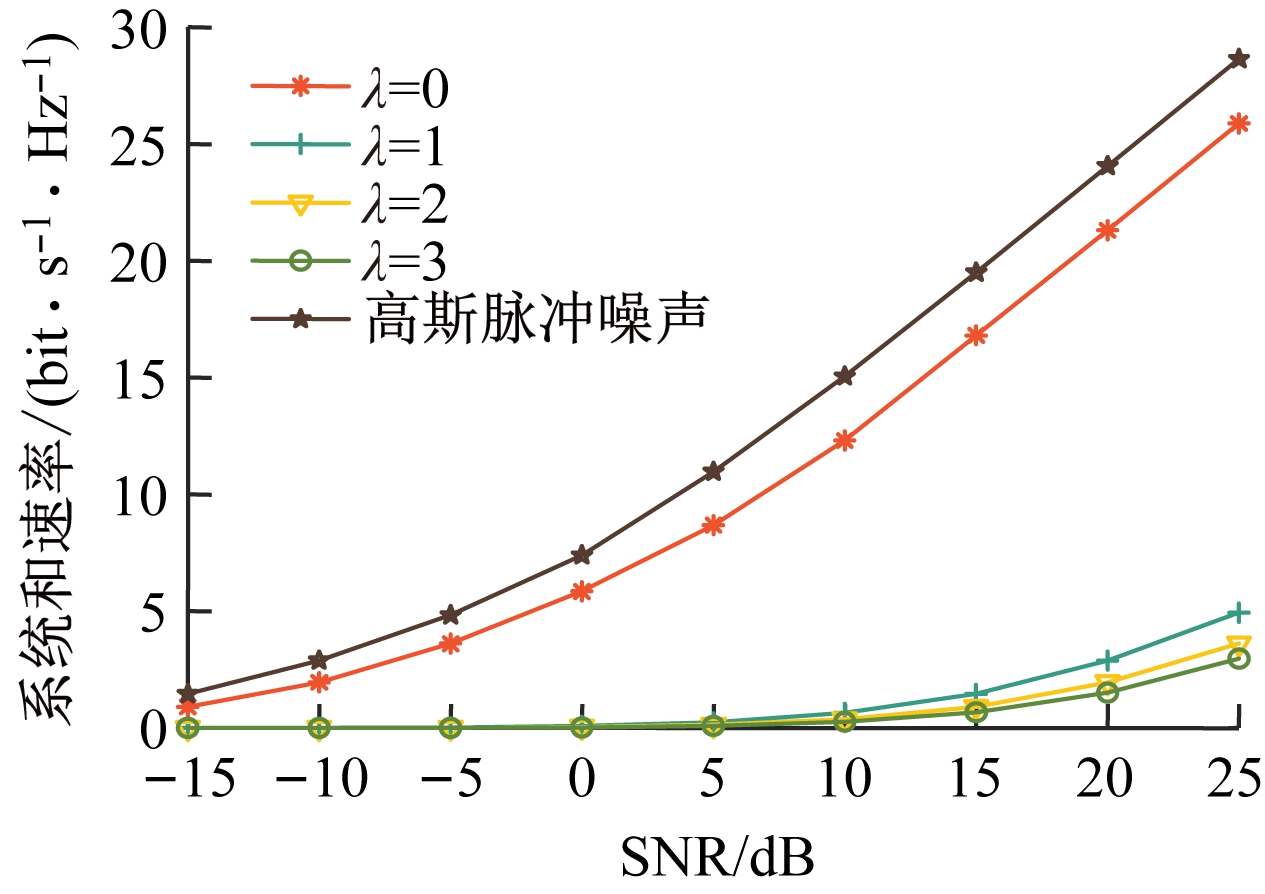
图3 不同状态下的系统和速率
Fig.3 The system sum-rate under different states
噪声状态为0、SNR为25 dB时,本文算法和SDR算法的系统和速率如图4所示。可以看出,7次迭代后本文算法达到收敛,而SDR算法在15次迭代后才达到收敛,本文算法的收敛速度是SDR算法的2倍多。这是因为SDR算法中嵌套了D.C.算法,2层循环导致算法的收敛速度较慢,而本文算法采用二次转换来解耦,算法中只包含1层循环。当算法达到收敛时,本文算法的系统和速率性能略有提升,进一步验证了本文算法的优越性。当基站天线和机器型通信设备的数量很大时,本文算法的收敛优势会更明显。
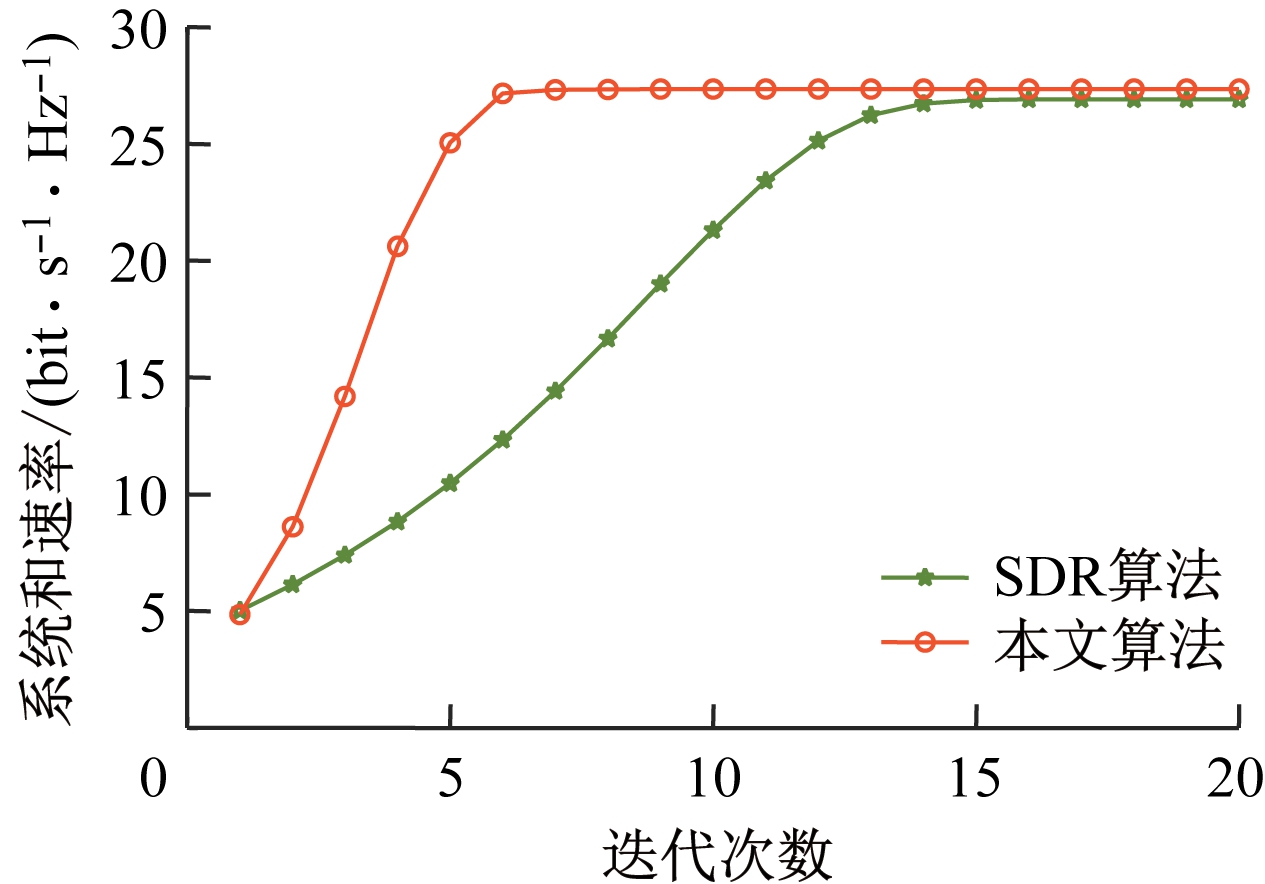
图4 不同算法的系统和速率收敛速度
Fig.4 Convergence speed of system sum-rate of
different algorithms
根据式(15),得到本文算法和SDR算法在MCA噪声模型下的平均系统和速率,如图5所示。可见,本文算法与SDR算法的系统和速率十分相近,进一步验证了本文算法的有效性。
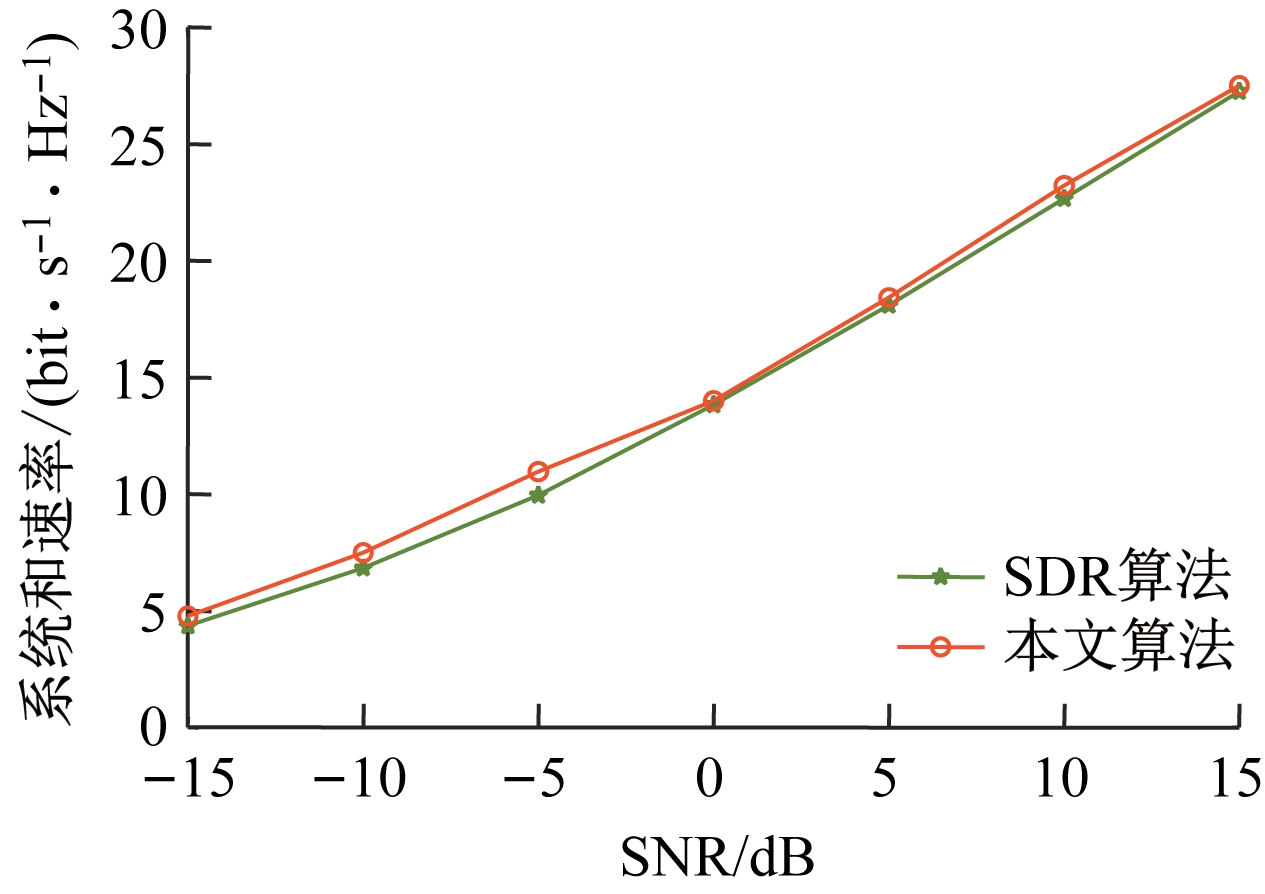
图5 不同算法的系统和速率
Fig.5 The system sum-rate of different algorithms
4.2 深度削减噪声消除方案性能验证
为评估所提出的深度削减噪声消除方案的性能,需选择合适的门限阈值T和深度因子μ,使![]() 的值最小,即
的值最小,即
(35)
本文采用Broydon-Fletcher-Goldfarb-Shanno (BFGS)算法来迭代求解式,从而得到门限阈值和深度因子的最优值[21]。
深度削减因子μ和门限阈值T对深度削减噪声消除方案性能的影响如图6和图7所示。可以明显看出,深度削减因子μ和幅度削减门限阈值T对系统的输出SNR和SER至关重要。这是因为当阈值T太低时,会引起大部分OFDM信号变为零,从而导致输出SNR 大大降低;相反地,当阈值T接近于无穷大时,相当于没有进行脉冲噪声消除,从而引起系统性能下降。当削减因子μ趋近于零时,与传统的削减噪声消除方案性能一致;当μ趋近于无穷大时,深度削减方案变为消隐脉冲噪声消除方案,从而影响系统性能。
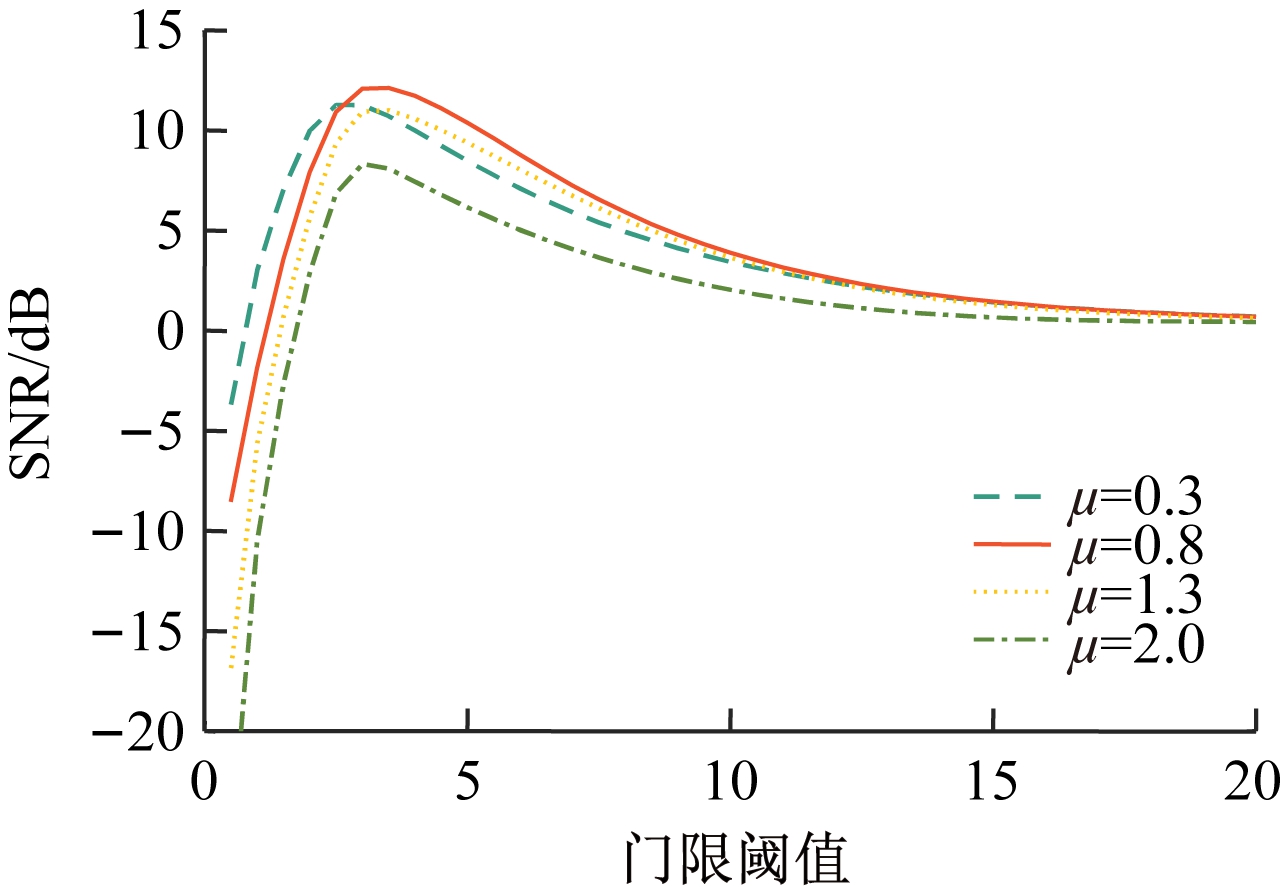
图6 不同深度削减因子μ和阈值T时的输出SNR
Fig.6 Output SNR when adopting different deep
reduction μ and thresholds T
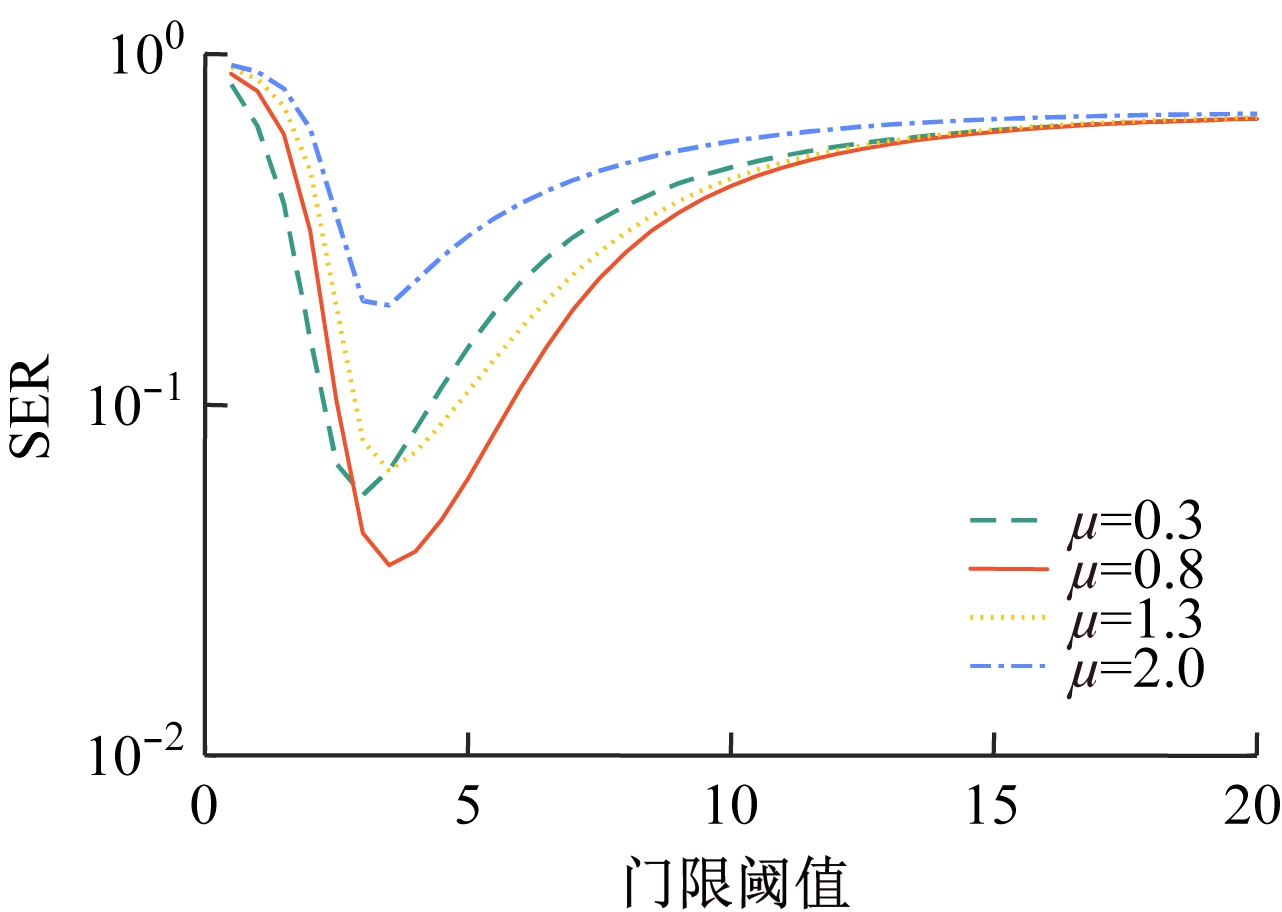
图7 不同深度削减因子μ和阈值T时的SER
Fig.7 SER when adopting different deep reduction
μ and thresholds T
当深度削减因子为最优时,4种脉冲噪声消除方案的输出SNR和SER如图8和图9所示。可以明显看出,本文提出的深度削减脉冲噪声消除方案和主流的消隐、削减、混合3种非线性脉冲噪声消除方案的最佳门限阈值T不同。主流方案中,混合脉冲消除方案性能最佳。而深度削减脉冲噪声消除方案的SER比混合脉冲消除方案低24%,其输出SNR最高,SER最低,性能最优。
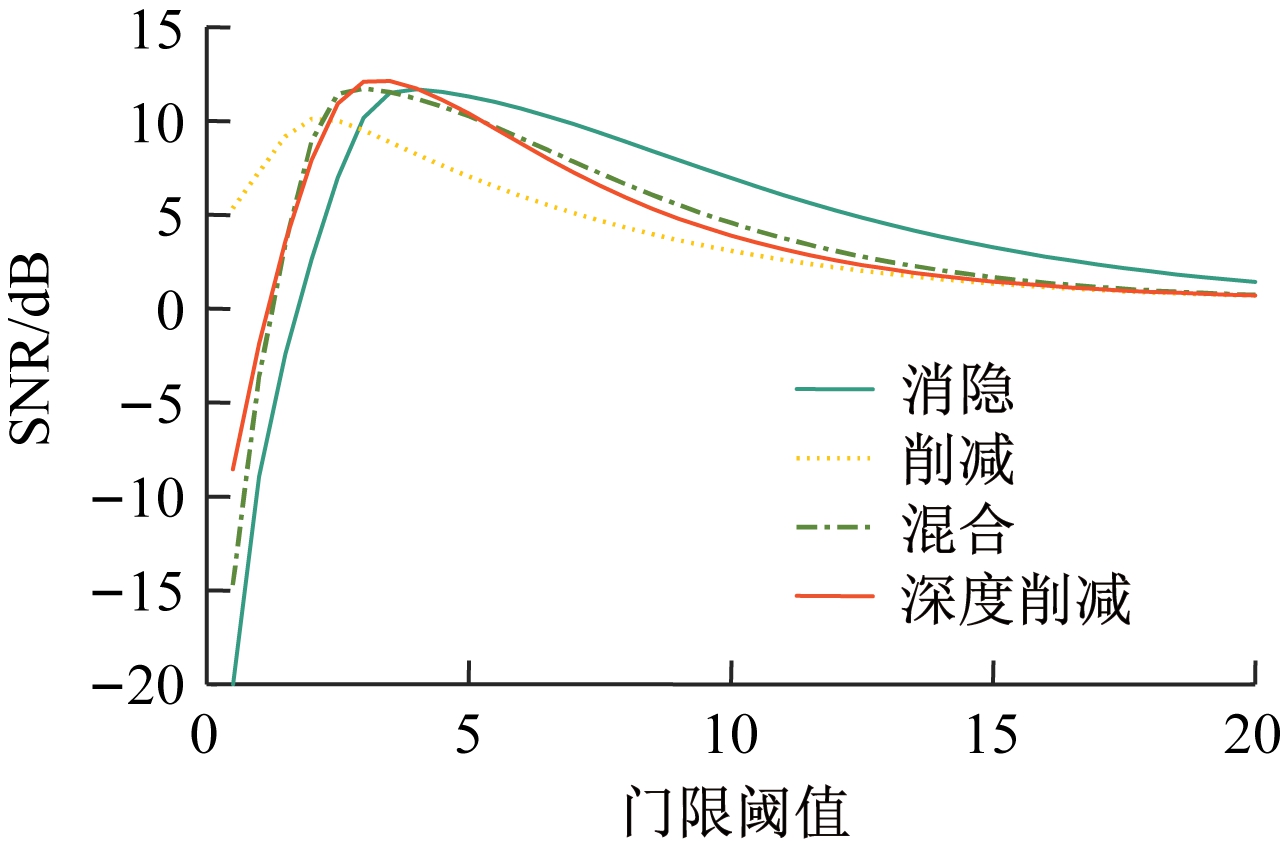
图8 不同脉冲噪声消除方案的输出SNR
Fig.8 Output SNR of different impulse noise
elimination schemes
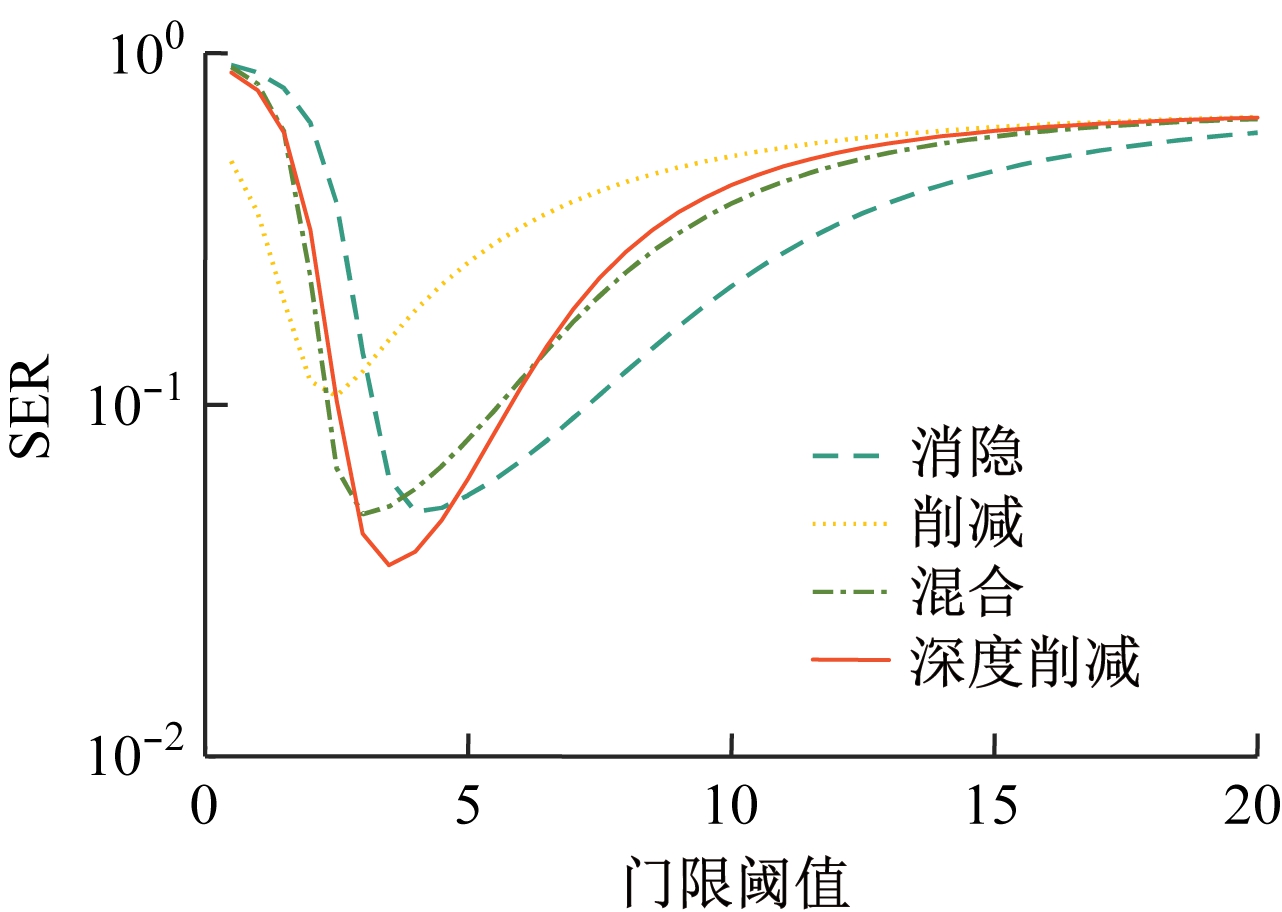
图9 不同脉冲噪声消除方案的输出SER
Fig.9 Output SER of different impulse noise
elimination schemes
5 结论
(1) 建立了联合收发端设计的MISO-OFDM系统模型,以研究脉冲噪声下工业无线通信系统和速率,保证通信的可靠性和有效性。
(2) 在发射端,设计了一种低复杂度的基于二次型转换的预编码算法,以最大化工业无线通信系统和速率。通过二次转换来解决系统和速率的预编码耦合问题,将分式规划问题转换为凸优化问题,在保证算法性能的前提下实现了较低的算法复杂度。
(3) 在接收端,设计了一种接收端深度削减脉冲噪声消除方案,通过选择合适的深度削减因子和削减门限阈值来提高通信可靠性,抑制脉冲噪声对SER的影响。
(4) 仿真结果表明:在MCA噪声模型下,基于二次型转换的预编码算法与SDR算法的系统和速率十分相近,验证了所提预编码算法的有效性;与主流的消隐、削减、混合3种非线性脉冲噪声消除方案相比,深度削减脉冲噪声消除方案的输出SNR最高,SER最低,SER比主流的最佳方案低24%,性能最优。
[1] 孙彦景,霍羽,陈岩,等.矿山动态协同作业场景无线通信关键技术[J].煤炭学报,2021,46(1):321-332.
SUN Yanjing,HUO Yu,CHEN Yan,et al.Key technology of service attribute driven wireless communication for dynamic cooperative operations in mining scenarios[J].Journal of China Coal Society,2021,46(1):321-332.
[2] 田震,荆双喜,赵丽娟,等.采煤机噪声与振动特性研究[J].工矿自动化,2019,45(3):23-28.
TIAN Zhen,JING Shuangxi,ZHAO Lijuan,et al.Research on noise and vibration characteristics of shearer[J].Industry and Mine Automation,2019,45(3):23-28.
[3] 张克,刘留,袁泽,等.工业物联网无线信道与噪声特性[J].电信科学,2018,34(8):87-97.
ZHANG Ke,LIU Liu,YUAN Ze,et al.Wireless channel and noise characteristics in Industrial Internet of things[J].Telecommunications Science,2018,34(8):87-97.
[4] ZHIDKOV S V.Performance analysis and optimization of OFDM receiver with blanking nonlinearity in impulsive noise environment[J].IEEE Transactions on Vehicular Technology,2006,55(1):234-242.
[5] ZHIDKOV S V.Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J].IEEE Transactions on Communications,2008,56(1):5-9.
[6] ANDREI M,TRIFINA L,TARNICERIU D.Capacity of Middleton Class-A impulsive noise channel with binary input[J].Applied Mathematics & Information Sciences,2015,9(3):1291-1298.
[7] SUSHMA B S,ROOPESH R,GURUGOPINATH S,et al.Performance characterization of broadband powerline communication for Internet-of-things[C]//International Conference on Wireless Communications Signal Processing and Networking,Chennai,2019.
[8] NIKFAR B,AKBUDAK T,VINCK A J H.MIMO capacity of class a impulsive noise channel for different levels of information availability at transmitter[C]//18th IEEE International Symposium on Power Line Communications & Its Applications,Glasgow,2014.
[9] BI T,CHEN X.Research on the linear precoding algorithm based on 5G mobile communication technology[C]//IEEE International Conference on Artificial Intelligence and Information Systems,Dalian,2020.
[10] PENG J.Linear precoding design for MIMO-PLC systems[J].Tsinghua Science and Technology,2015,20(2):155-163.
[11] ZHOU X,LI J.A novel precoding and impulsive noise mitigation scheme for MIMO power line communication systems[J].IEEE Systems Journal,2019,13(1):6-17.
[12] CHITRE M A,POTTER J R,ONG S H.Optimal and near-optimal signal detection in snapping shrimp dominated ambient noise[J].IEEE Journal of Oceanic Engineering,2006,31(2):497-503.
[13] LIU S,YANG F,DING W,et al.Double kill:compressive-sensing-based narrow-band interference and impulsive noise mitigation for vehicular communications[J].IEEE Transactions on Vehicular Technology,2016,65(7):5099-5109.
[14] CHEN P,RONG Y,NORDHOLM S,et al.Joint channel estimation and impulsive noise mitigation in underwater acoustic OFDM communication systems[J].IEEE Transactions on Wireless Communications,2017,16(9):6165-6178.
[15] ADEBISI B,ANOH K,RABIE K M,et al.A new approach to peak threshold estimation for impulsive noise reduction over power line fading channels[J].IEEE Systems Journal,2019,13(2):1682-1693.
[16] JUWONO F H,REINE R,LIU L,et al.Performance of impulsive noise blanking in precoded OFDM-based PLC systems[C]// IEEE International Conference on Communication Systems,Shenzhen,2016.
[17] SHONGWE T,VINCK A H,FERREIRA H C.On impulse noise and its models[C]//18th IEEE International Symposium on Power Line Communications and Its Applications,Glasgow,2014.
[18] SHEN K,YU W.Fractional programming for communication systems-part I:power control and beamforming[J].IEEE Transactions on Signal Processing,2018,66(10):2616-2630.
[19] JUWONO F H,GUO Q,HUANG D,et al.Deep clipping for impulsive noise mitigation in OFDM-based power-line communications[J].IEEE Transactions on Power Delivery,2014,29(3):1335-1343.
[20] PHAN A H,TUAN H D,KHA H H,et al.Iterative D.C.optimization of precoding in wireless MIMO relaying[J].IEEE Transactions on Wireless Communications,2013,12(4):1617-1627.
[21] RAO S S.Engineering optimization theory and practice[M].4th edition.Hoboken:John Wiley,2009.
