0 引言
煤矿井下环境复杂,设备与作业人员众多,人、机、物等目标定位的精确性和可靠性是矿井安全生产的重要保障和应急救援的必要手段[1-2],也是实现机器协同工作和智能化无人生产的关键技术[3-5]。
文献[6-8]对基于标签的井下定位技术进行了研究。文献[6]采用双标签,在同一目标上部署2个水平或垂直标签,通过标签与标签、标签与基站的约束关系构造优化函数,并用双向迭代求精法求解定位结果;文献[7]提出了一种在ZigBee通信协议框架下的联合算法,使用链路质量指标对接收信号强度数据进行滤波,对信道参数和环境噪声参数进行联合估计,并依据环境噪声参数对距离估计进行补偿;文献[8]提出了一种区间分段式视距节点合作定位算法,根据学习向量量化聚类分段阈值判定未知节点所属定位区间,当参考节点信号不满足阈值条件时,利用信道状态信息寻找视距路径节点,减少远距离参考节点的使用,提高了系统稳定性和定位精度。上述研究均采用有源定位技术,即在井下目标位置放置定位设备(标签),将目标定位问题转换为标签定位问题。当标签调制查询信号时,通过提取反向散射信号的相位[9]、时延[10]和功率[11],估计目标位置信息。然而在井下复杂环境中,由于工作人员不便携带标签、作业途中易丢失标签等原因,传统的有源定位技术在井下目标定位应用中受到限制[12]。针对此类场景,有学者提出了不依赖于定位设备(标签)的无源定位技术[13-14]。该技术主要采用几何法和指纹法。几何法利用目标对无线链路的影响,确定被目标影响的链路后,找出它们的交点,对交点进行数据处理,推断其具体位置[15-16]。指纹法是在离线阶段收集目标在不同位置的信号特征(接收信号强度指示、幅值、信道状态信息等)作为指纹,建立离线无线电地图,在在线阶段将当前的信号特征测量值与无线电地图中的指纹进行比较,估算目标位置[17-18]。
尽管上述方法能够实现无标签定位,但煤矿井下工作环境复杂、障碍物较多,存在密集的多径干扰,导致定位精度低,所以现有的无标签目标定位方法并不适合直接应用于井下。本文提出一种空间和频率分集联合的矿井无标签目标定位方法。该方法基于傅里叶域非均匀采样原理实现目标定位;采用无源宽带谐波标签生成所需谐波信号,消除发射天线引入的基频干扰;利用不同谐波标签的空间多样性和谐波信号的频率多样性,融合多通道信息,实现空间和频率分集联合,解决采样信息不足导致的低定位精度问题;利用差分接收算法抑制下行链路多径干扰,消除多径干扰引起的相位误差,提高矿井无标签目标定位精度。
1 矿井无标签目标定位系统
矿井无标签目标定位系统主要包括发射天线、接收天线和无源宽带谐波标签,如图1所示。发射天线至少为1个,接收天线为多个。谐波标签和接收天线位置需预先校准。
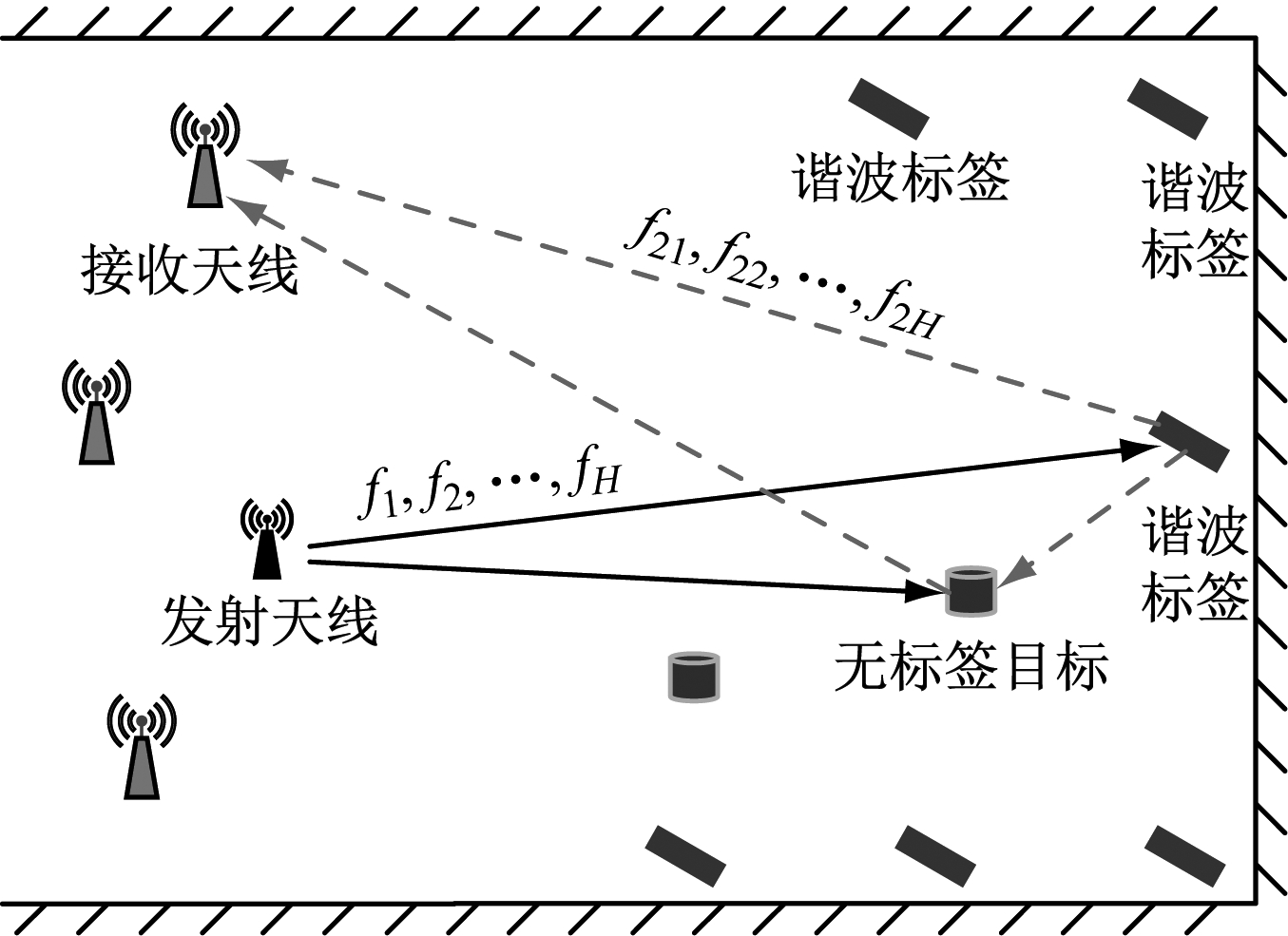
图1 矿井无标签目标定位系统
Fig.1 Mine tagless target location system
无标签目标定位期间,发射天线发出一系列基频查询信号ah(t),其频率为fh(h=1,2,…,H,H为频率个数),且f1 < f2 <…< fH。第m(m=1,2,…,M,M为谐波标签个数)个谐波标签响应查询信号,并由内部非线性元件产生二次谐波信号sm(t),其频率为f2h,f2h=2fh[19]。此时频率为f2h的电磁波作为系统定位采用的射频信号,即接收天线只接收频率为f2h的谐波信号,不再接收频率为fh的载波信号,消除了发射天线引入的频率为fh的多径干扰信号影响。
由谐波标签发出的二次谐波信号经无标签目标反向散射后到达接收天线。接收天线得到单频和单标签下的一次定位结果,该结果是不准确的。重复上述定位过程,将获得多个标签和多个频率下的定位结果,即通过空间和频率分集联合,融合多通道信息,实现准确定位。
2 傅里叶域非均匀采样原理
无标签目标定位本质上是接收信号由时域变换到波数域后目标散射函数在傅里叶域中的非均匀采样过程。球坐标系下谐波标签、无标签目标和接收天线组成的定位模型如图2所示。
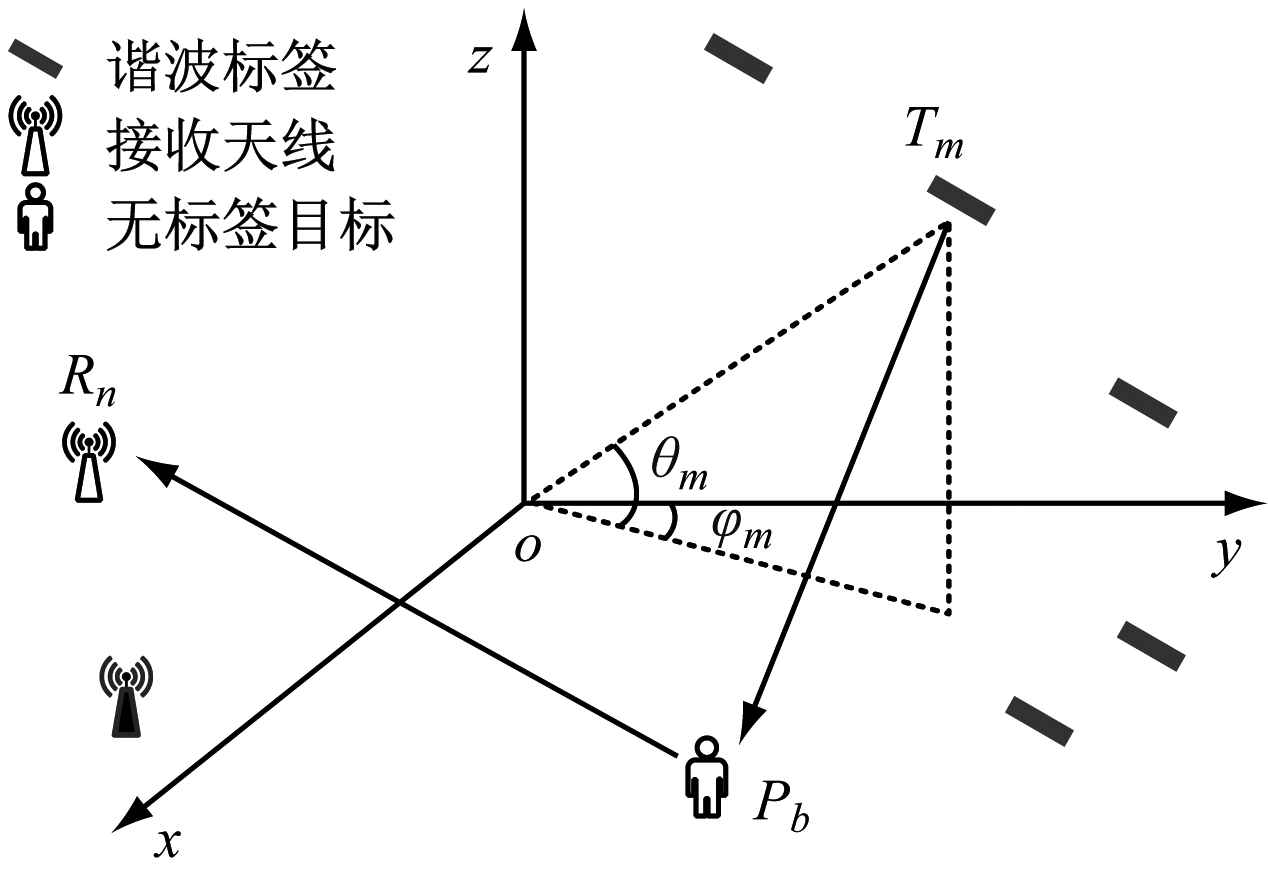
图2 球坐标下定位模型
Fig.2 System model under spherical coordinates
图2中,Rn=(rn, θn, φn)和Tm=(rm, θm, φm)分别为第n个接收天线和第m个谐波标签的球面位置坐标,Pb=(r,θ,φ)为第b个目标散射点坐标。rn, θn, φn分别为第n个接收天线距原点距离、俯仰角和方位角;rm, θm, φm分别为第m个谐波标签距原点距离、俯仰角和方位角;r,θ,φ分别为目标散射点距原点距离、俯仰角和方位角。为了分析方便,假设不存在直达波及其他多径干扰,只有目标回波信号。发射天线发射基频查询信号ah(t),谐波标签被唤醒并响应查询信号,产生并发射二次谐波信号:
sm(t)=Gmexp(j2πf2ht+φm)
(1)
式中:t为时间;Gm为二次谐波信号幅度;φm为二次谐波信号的初始相位,由谐波标签与发射天线的距离决定。
根据信号传播路径,得到第m个谐波标签发射的信号经过无标签目标反向散射后到达第n个接收天线的信号:
sm,n(t,r)=σ(P)Gmexp(j2πf2h(t-τmn)+φm)=
(2)
式中:σ(P)为无标签目标的散射函数;τmn为第m个谐波标签发射信号经目标散射后到达第n个接收天线的时延;c为光速。
在远场条件下,式(2)可表示为
sm,n(t,r)=![]()
sin φ(cos θmsin φm+cos θnsin φn)-
rcos θcos φ(cos θmcos φm+
(3)
通过参考信号(式(4))解调式(3),得到解调后的回波信号(式(5))。
(4)
sm,n(t,r)=![]()
(cos θmsin φm+cos θnsin φn)+rcos θ×
cos φ(cos θmcos φm+cos θncos φn)+
(5)
在球坐标系对应三维直角坐标系oxyz中,令x=rcos θsin φ,y=rcos θcos φ,z=rsin θ,则式(5)转换为
sm,n(t,r)=![]() θmsin φm+cos θnsin
θmsin φm+cos θnsin ![]() θmcos φm+cos θn×
θmcos φm+cos θn×
![]()
(6)
将sm,n(t,r)从时域变换到波数域,得
Dmn(kx,ky,kz)=σ(P)Gmexp(j2π(xkx+
yky+zkz))
(7)
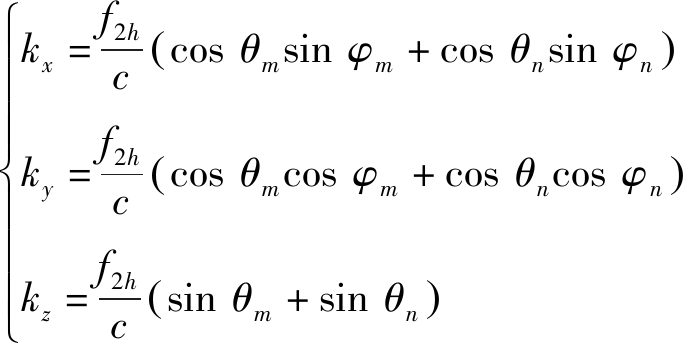
(8)
(kx, ky, kz)称为空间谱域或波数域。假设目标区域空间为V,则由第m个谐波标签和第n个接收天线获得的回波信号为
Dmn(kx,ky,kz)=![]()
yky+zkz))dxdydz
(9)
式(9)表明空间谱回波信号Dmn(kx,ky,kz)和目标散射函数σ(P)之间存在傅里叶变换关系。因此,可通过傅里叶逆变换恢复目标散射函数:
σ(P)=![]()
yky+zkz))dkxdkydkz
(10)
式中K为空间谱填充范围。
目标散射函数恢复可以理解为一个采样过程,每组谐波标签和接收天线构成一个观测通道,一个通道内在每个频率上的一次快拍数据相当于一个采样点,并映射为空间谱域中的一个分布点(kx,ky,kz),所有通道的回波信号Dmn(kx,ky,kz)映射为系统的空间谱填充。密集的空间谱填充可以准确地实现目标定位,而稀疏和局部填充会导致定位结果不准确和重影。
由式(8)可知
(11)
可见傅里叶域的采样被限制在一个直径为4f2h/c的球内,谐波标签发射信号的最大传输频率为f2H。因此在x,y,z轴方向上的最佳分辨率为c/(4f2H)。
由式(8)可看出,频率多样性及谐波标签和接收天线的角度多样性是很重要的采样资源,它们共同确定了空间谱域的覆盖范围,且其半径由最大基频查询信号频率决定。由于采样数据是离散的,所以将式(8)中的变量(kx,ky,kz)利用Jacob行列式Jh,m,n转换为(fh,θm,φm),得到转换后的目标定位函数σh,m,n(P),即由第h个频率、第m个谐波标签和第n个接收天线确定的定位结果。
Jh,m,n=![]() θm[cos θncos θmcos(φn-φm)+1+sin θnsin θm]
θm[cos θncos θmcos(φn-φm)+1+sin θnsin θm]
(12)
σh,m,n(P)=![]()
(13)
式中N为接收天线个数。
融合M个谐波标签、N个接收天线和H个基频查询信号频率的数据,得到目标定位结果:
(14)
由此可得球坐标系下的无标签目标定位方法。由于标签、目标、接收天线相对静止,所以可通过一次快拍获得目标的位置信息。由式(13)可看出,球坐标系下目标位置是在离散化区域进行匹配搜索,并融合各分布式通道的投影进行滤波重建的结果。
3 目标定位
3.1 信号模型
对于每个采样周期,在初始化阶段已识别并定位了M个谐波标签,每次选择1个标签响应发射天线,以减少标签间的干扰。发射天线发射的基频查询信号为
ah(t)=Ahexp(j2πfht+jγh)
(15)
式中Ah,γh分别为第h个基频查询信号的幅值和初始相位。
设矿井无标签目标定位系统中存在N个接收天线,空间中存在频率为fh和f2h的信号,通过带宽足够大的滤波器滤除fh及其附近频率的自干扰和直接路径干扰信号,只接收频率为f2h的信号。对于第m个谐波标签发射信号sm(t),第n个接收天线接收信号Dh,m,n(t)可分为两部分:谐波标签到接收天线的直接路径信号及地面和墙壁到接收天线的多径信号![]() 由目标引起的反向散射信号dh,m,n(t)。即
由目标引起的反向散射信号dh,m,n(t)。即
(16)
![]() 可表示为
可表示为
(17)
![]()
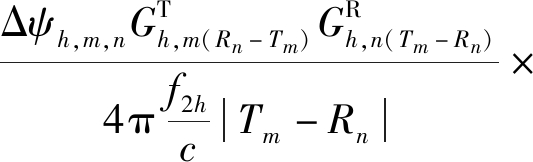
(18)
式中:Δψh,m,n,Δεh,m,n分别为多径干扰信号相对于直接路径信号的幅度和相位变化;![]() 分别为谐波标签发射信号和接收天线接收信号在频率f2h处的幅度增益。
分别为谐波标签发射信号和接收天线接收信号在频率f2h处的幅度增益。
假设目标中存在B个散射点,则dh,m,n(t)可表示为
dh,m,n(t)=sm(t)ah,m,n
(19)
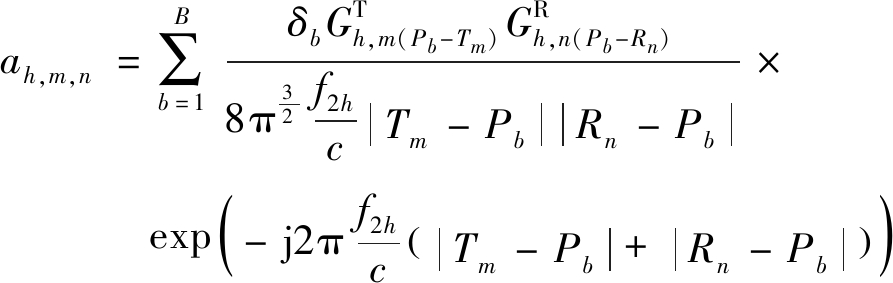
(20)
式中δb为与目标反射面积呈一定比例的复振幅。
3.2 差分接收算法
式(1)中标签初始相位φm是未知的,但是在接收端进行解调时需要已知相位信息。因多径会引起相位估计误差,采用差分接收算法来避免该问题。对于第m个谐波标签发射的二次谐波信号sm(t),设第n个、第q(q≠n)个接收天线接收信号的比值为
(21)
Ah,m,n,q与未知的初始相位φm无关,由信道特性决定,且可在目标不存在的情况下预先校准。目标不存在时,第n个接收天线的接收信号即![]() 表示为
表示为
(22)
此时第n个、第q个接收天线接收信号的比值为
(23)
定义从第m个标签到n个接收天线的差分接收信号为
uh,m,n=![]()
(24)
由目标引起的反向散射信号相比于直接路径信号和多径信号小得多,可近似为
(25)
将式(25)代入式(24),得
(26)
其中
![]()
![]()
(27)
γh(Pb,Tm,Rn)=![]()
(28)
3.3 高精度定位
根据谐波标签与接收天线的距离,去除直接路径信号,得到第n个接收天线的接收信号:
(29)
目标散射函数即目标位置的恢复来源于不同权值的Uh,m,n叠加。假设此时上行链路多径干扰已被抑制,式(29)可表示为
Uh,m,n=![]()
(30)
ΔUh,m,n=![]()
(31)
由于差分接收引入了除第n个接收天线外的其他接收天线信号,所以可通过平均N个接收天线的信号来减小式(30)和式(31)对定位精度的影响,将监测区域划分成若干个均匀大小的网格点,逐点搜索每个网格点,得到目标散射函数:
σ(P)=![]()
(32)
式中ωh,m,n为Uh,m,n权值。
根据式(32)得出相应σ(P),σ(P)最大值对应的散射点位置为目标定位结果。比较式(32)和式(12),可看出若ωh,m,n=Jh,m,n,即
ωh,m,n=![]()
(33)
式(32)所示σ(P)为式(12)的相同表达形式,且不需要远场假设。
3.4 目标定位流程
(1) 初始化阶段定位识别M个谐波标签,确定谐波标签位置Tm。
(2) 计算第m个谐波标签到第n个和第q个接收天线的信号比值Ah,m,n,q。
(3) 建立第m个谐波标签到第n个接收天线的差分接收信号uh,m,n。
(4) 去除谐波标签到接收天线的直达路径信号,得到接收信号Uh,m,n。
(5) 根据式(33)计算Uh,m,n权值ωh,m,n。
(6) 逐点搜索目标区域内每个位置,计算σ(P)。
4 仿真实验及结果分析
对矿井无标签目标定位方法进行Matlab仿真实验,结果及分析如下。
4.1 分集效果
为了直观比较谐波标签使用空间分集和频率分集前后的定位结果,在二维场景下选取2个点作为仿真实验的目标点,其坐标分别为(0 m,0 m),(0 m,0.2 m)。4组仿真参数见表1。
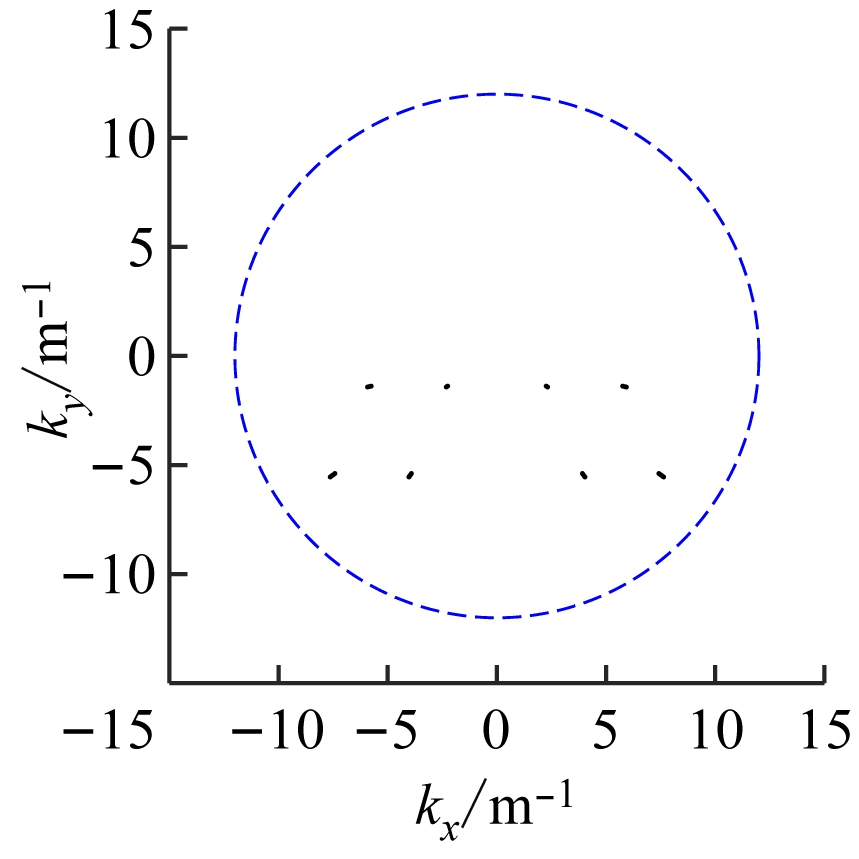
第1组实验设置4个谐波标签、2个接收天线及1个频率,仿真结果如图3所示。
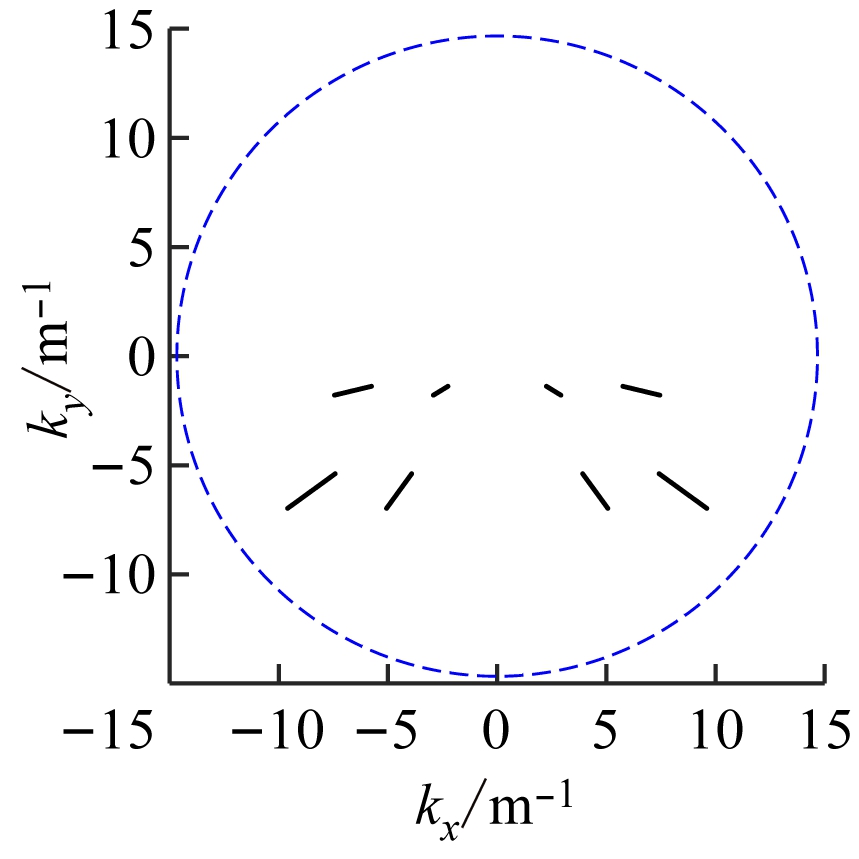
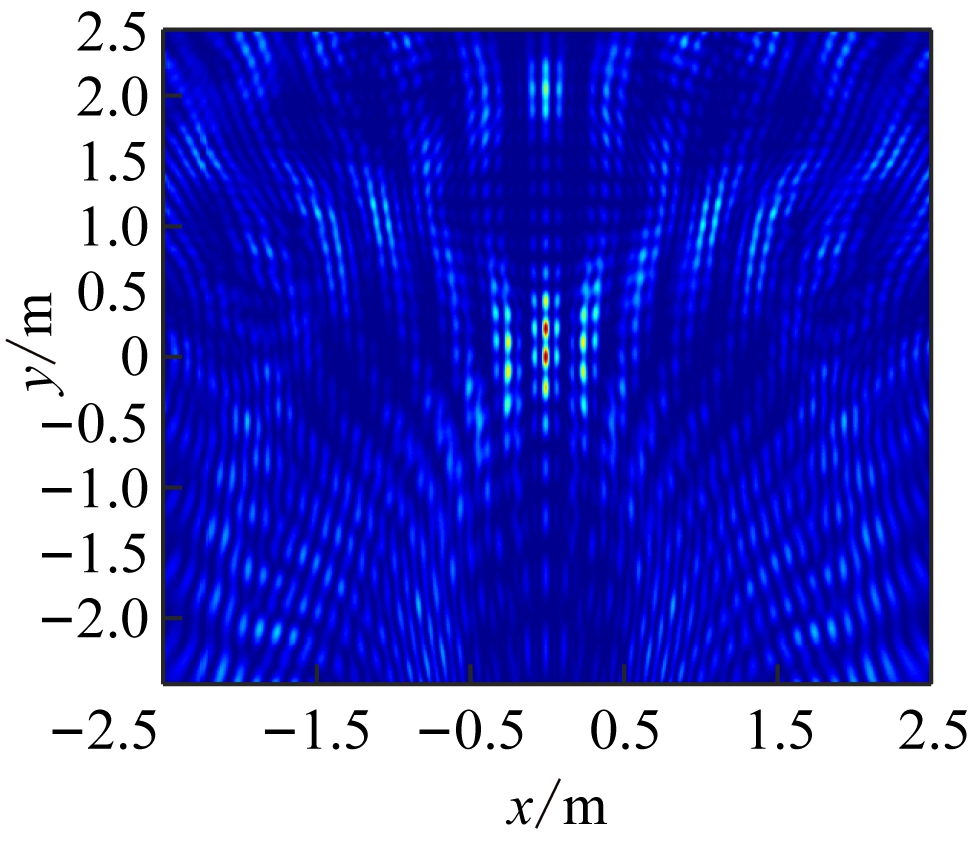
从图3可看出,第1组实验中波数域分布稀疏,无法填充空间谱,相应的定位结果不准确。在此基础上将频率增加至8个,实现频率分集,并进行第2组实验,结果如图4所示。
表1 仿真参数
Table 1 Simulation parameters
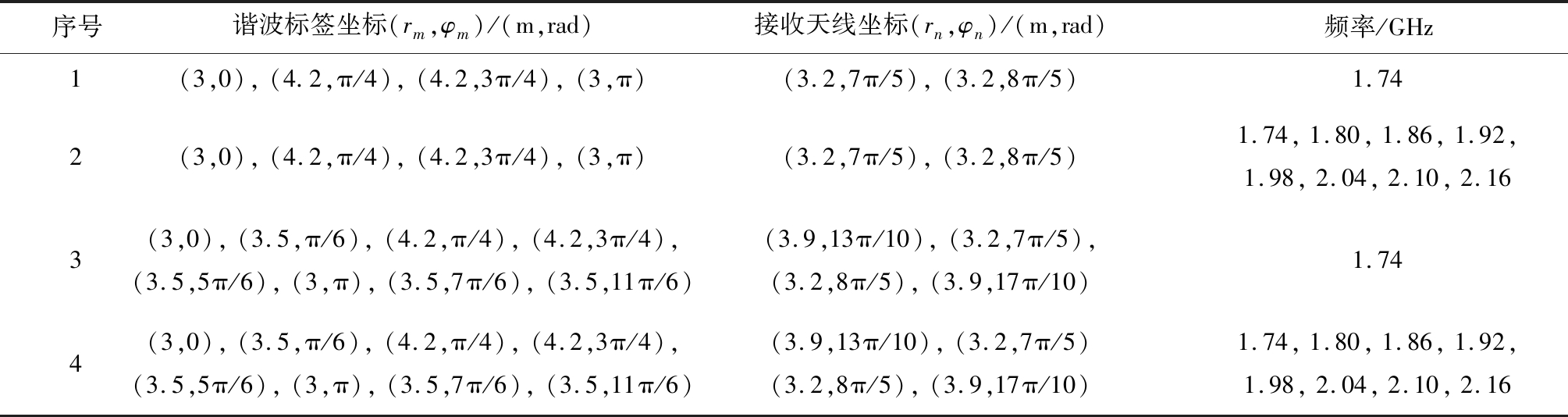
序号谐波标签坐标(rm,φm)/(m,rad)接收天线坐标(rn,φn)/(m,rad)频率/GHz1(3,0),(4.2,π/4),(4.2,3π/4),(3,π)(3.2,7π/5),(3.2,8π/5)1.742(3,0),(4.2,π/4),(4.2,3π/4),(3,π)(3.2,7π/5),(3.2,8π/5)1.74,1.80,1.86,1.92,1.98,2.04,2.10,2.163(3,0),(3.5,π/6),(4.2,π/4),(4.2,3π/4),(3.5,5π/6),(3,π),(3.5,7π/6),(3.5,11π/6)(3.9,13π/10),(3.2,7π/5),(3.2,8π/5),(3.9,17π/10)1.744(3,0),(3.5,π/6),(4.2,π/4),(4.2,3π/4),(3.5,5π/6),(3,π),(3.5,7π/6),(3.5,11π/6)(3.9,13π/10),(3.2,7π/5)(3.2,8π/5),(3.9,17π/10)1.74,1.80,1.86,1.92,1.98,2.04,2.10,2.16
(a) 波数域分布
(b) 定位结果
图3 第1组实验结果
Fig.3 The first group of experimental results
(a) 波数域分布
(b) 定位结果
图4 第2组实验结果
Fig.4 The second group of experimental results
从图4可看出,通过频率分集实现了比使用1个频率时更大的波数域覆盖,扩大了采样范围,提升了定位效果。但此时波数域覆盖区域较小,定位结果中存在虚像。
第3组实验在第1组实验设置基础上,保持频率不变,增加谐波标签和接收天线数量,实现空间分集。仿真结果如图5所示。
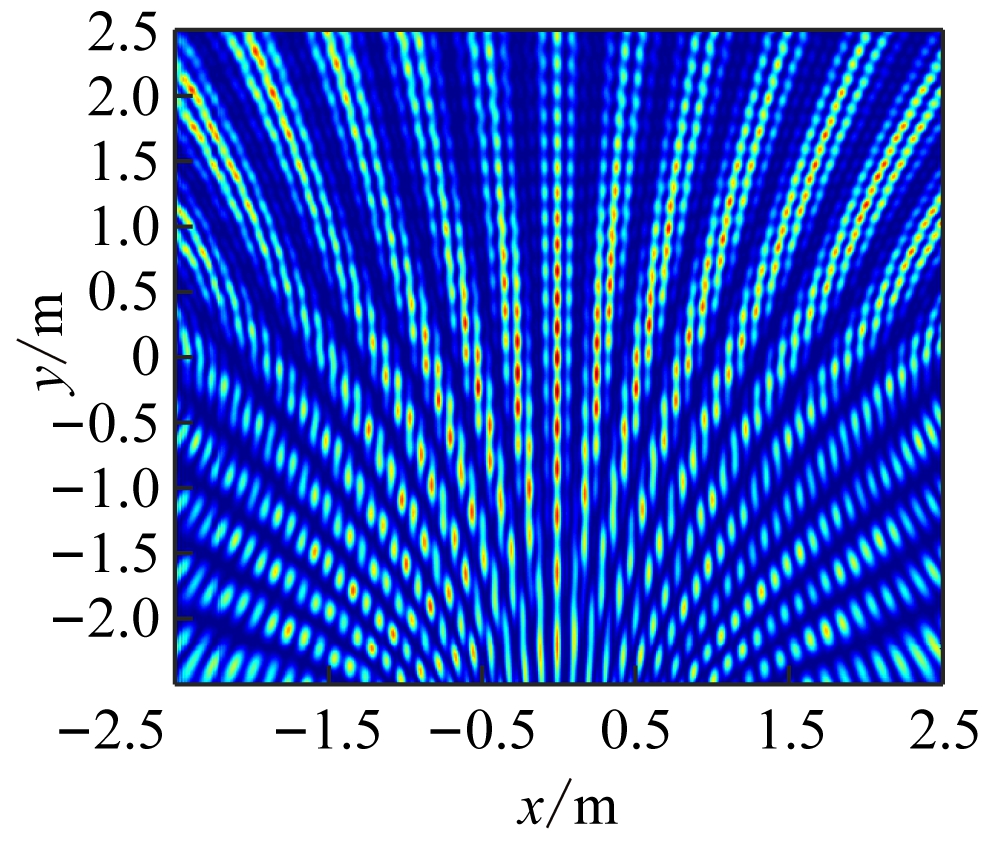
从图5可看出,通过空间分集扩大了波数域覆盖区域,相当于增加了傅里叶域的采样资源。虽然波数域的填充范围扩大,但填充过于稀疏,致使采样数据不足,定位结果中出现了一些虚假杂散的点。对此,第4组实验采用多频多标签和多接收天线,利用空间和频率分集联合,实现波数域的完整覆盖。仿真结果如图6所示。
从图6可看出,通过空间和频率分集联合,波数域覆盖范围扩展到整个kx轴和ky下半轴且较密集,使定位结果的分辨率得到显著提高,去除了虚像和重影,实现了目标准确定位。
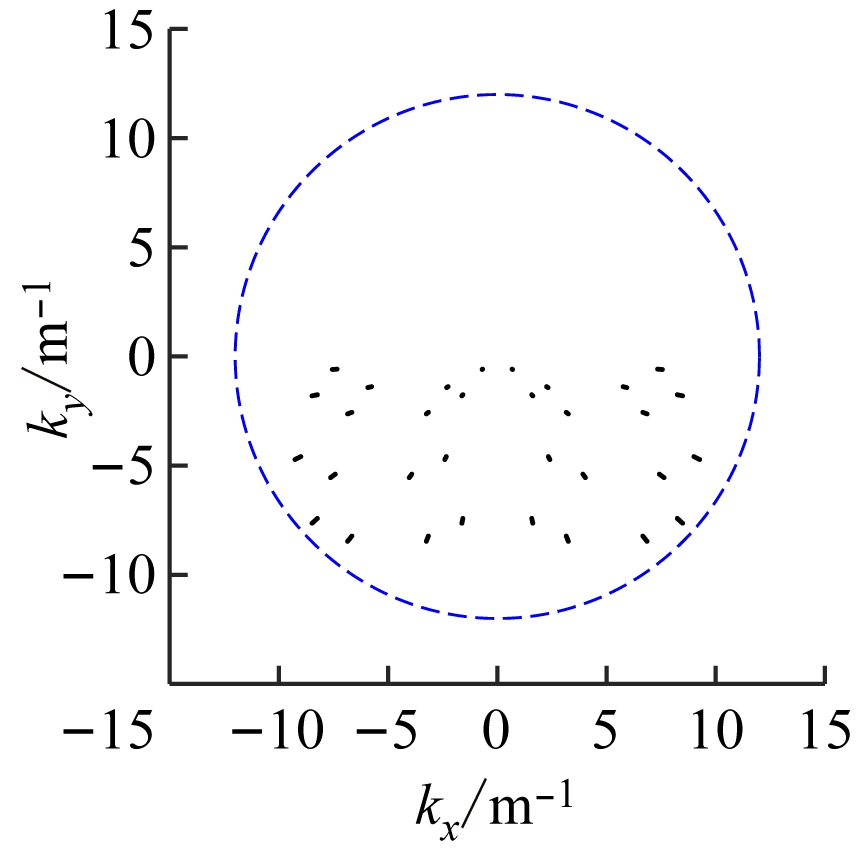
(a) 波数域分布
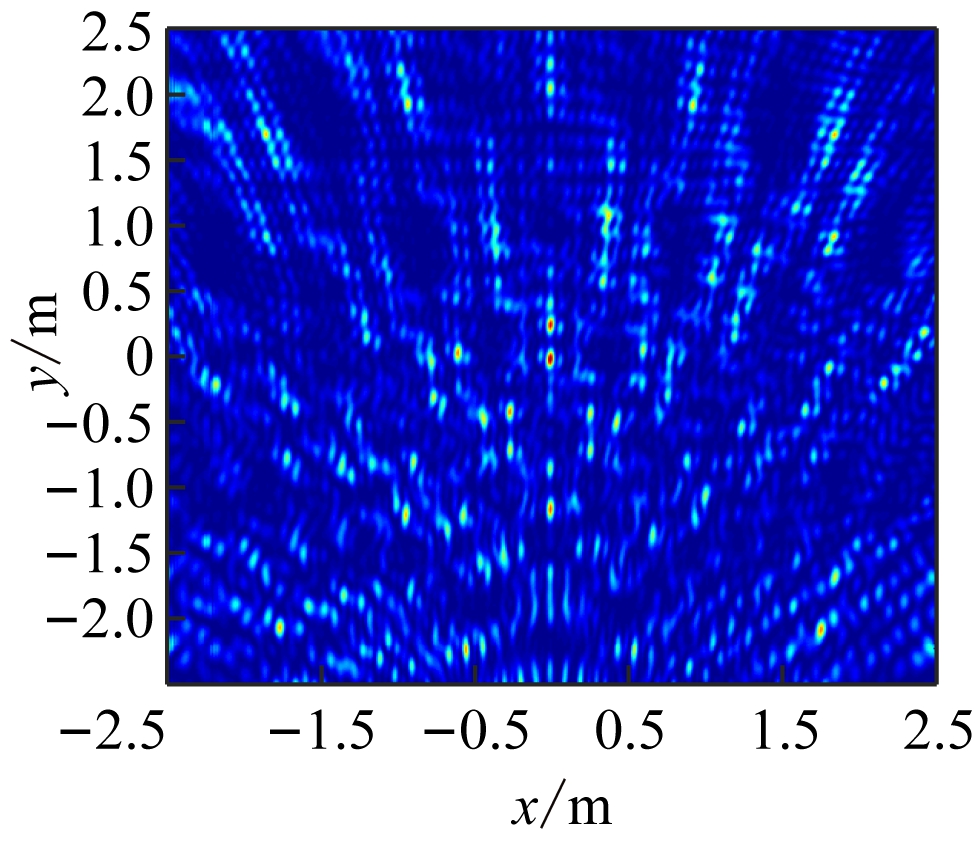
(b) 定位结果
图5 第3组实验结果
Fig.5 The third group of experimental results
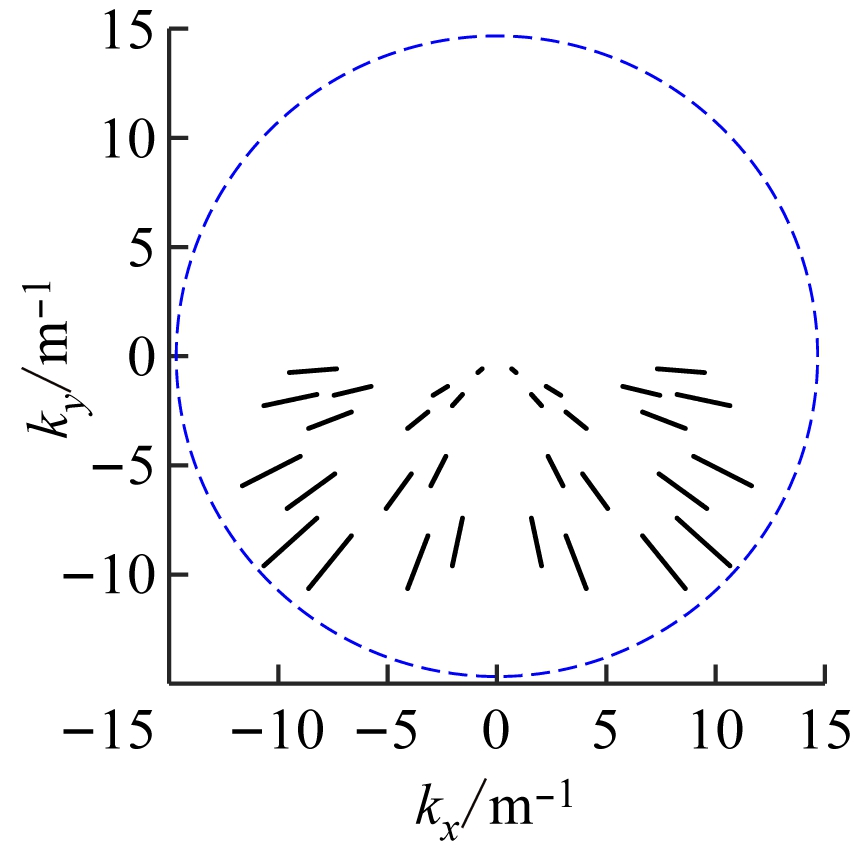
(a) 波数域分布
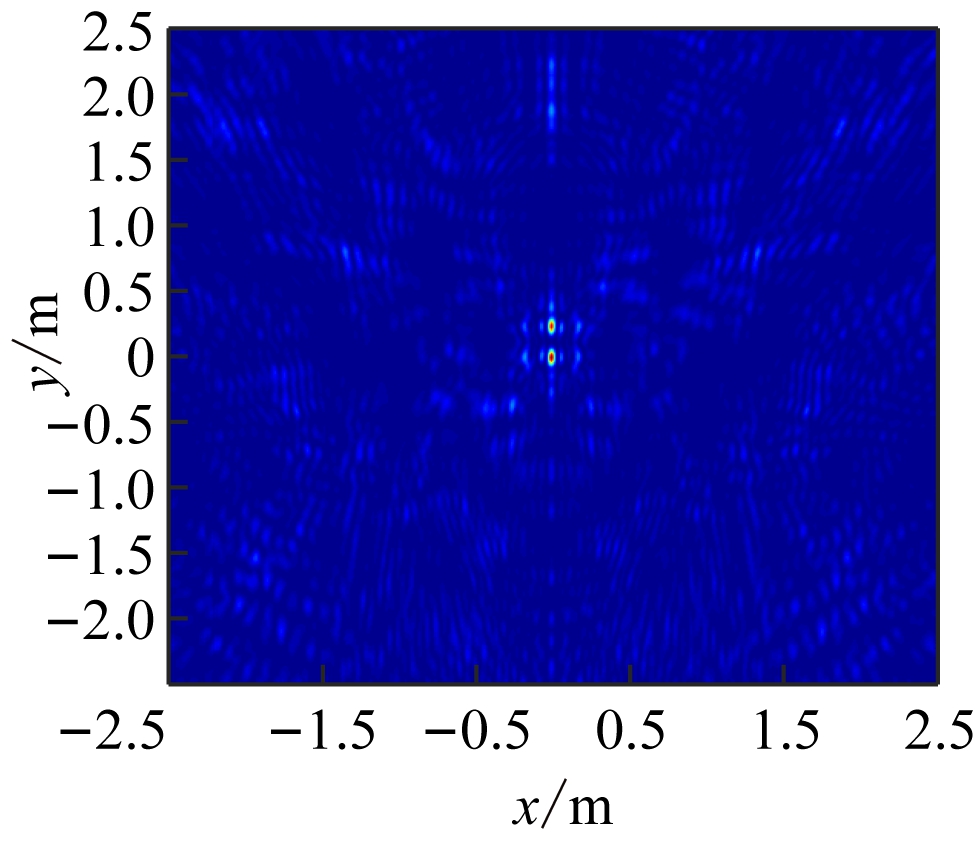
(b) 定位结果
图6 第4组实验结果
Fig.6 The fourth group of experimental results
4.2 差分接收效果
上述4组实验均采用了差分接收方法。为了验证差分接收对下行链路多径干扰的抑制效果,在第4组实验参数不变情况下,取消差分接收过程,所得定位结果如图7所示。
从图7可看出,当未对上行链路多径引起的相位误差进行处理,即未采用差分接收算法时,定位结果包含了多个可能的位置,无法准确定位目标。与图6(b)对比可知,差分接收算法对多径干扰有较好的抑制效果。
4.3 三维定位效果和定位误差
将仿真实验拓展到三维,采用8个标签、4个接收天线和8个频率,在5 m×5 m×5 m(长×宽×高)场景下选取5个目标点,定位结果如图8所示。
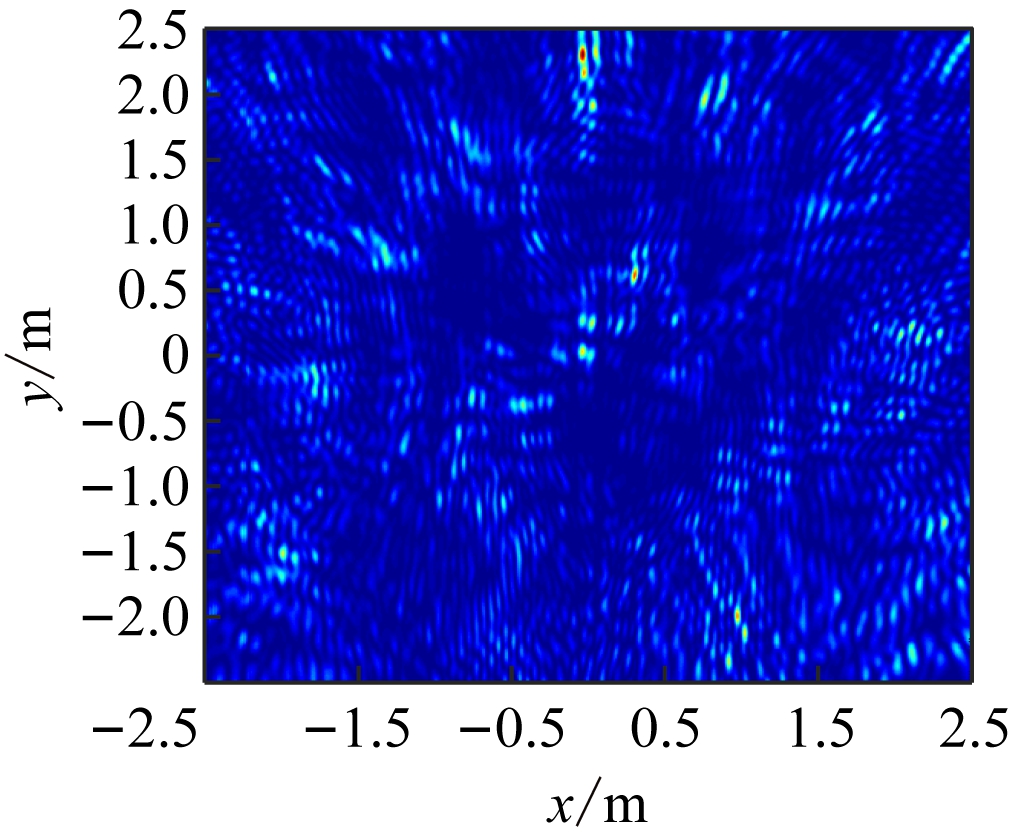
图7 无差分接收时定位结果
Fig.7 Location result without differential reception
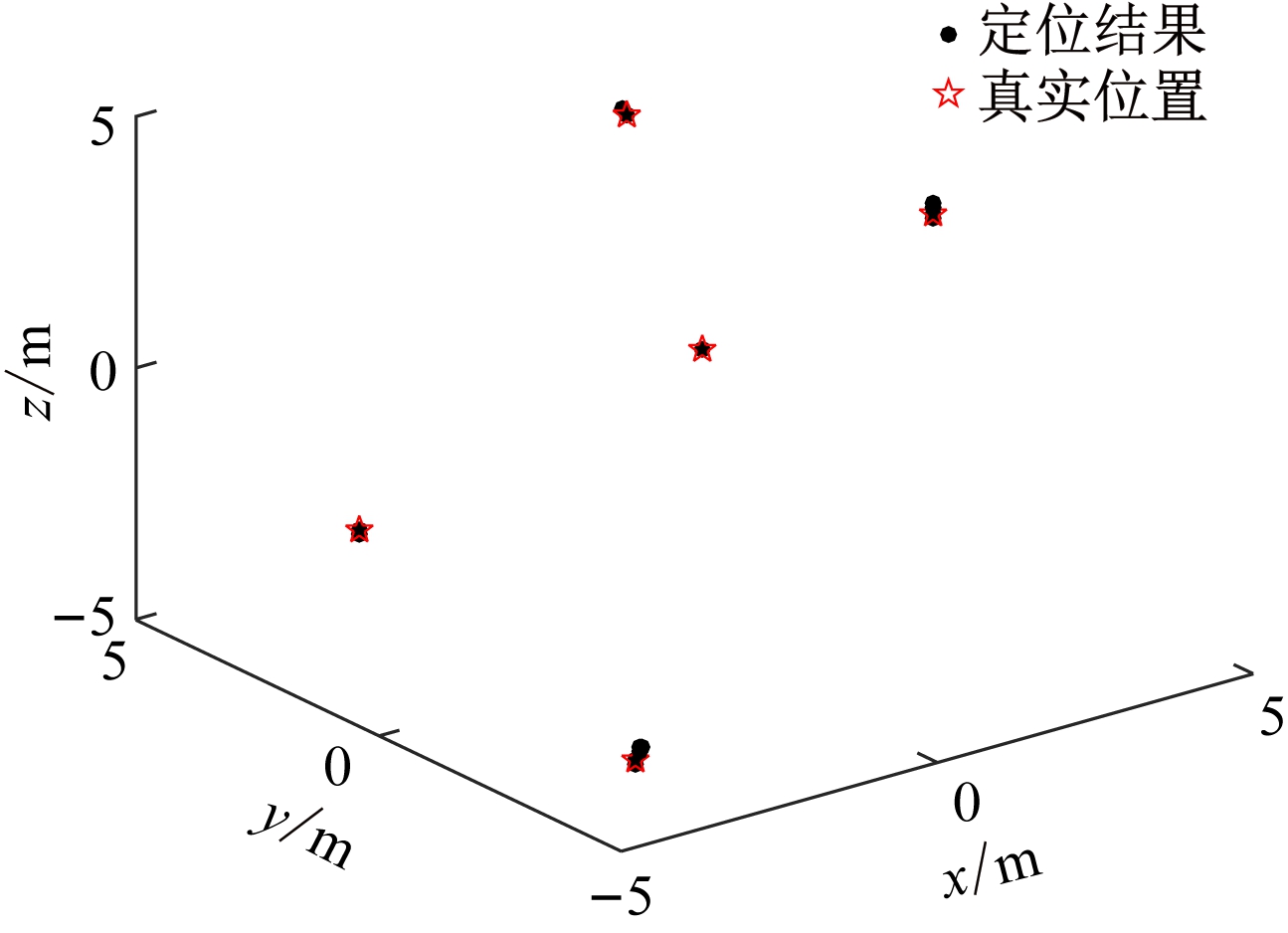
图8 三维场景下定位结果
Fig.8 Location result in 3D scene
将本文方法与RASS[13] 、D-watch[9]进行对比,分别进行100次仿真实验,得到3种方法的定位误差,如图9所示。RASS是一种基于RSS(Received Signal Stength,接收信号强度)变化的指纹定位方法,由于RSS为粗粒度信息,对距离并不敏感,所以RASS方法定位误差较大。D-watch通过AOA(Angle-of-Arrival,到达角度)峰值变化检测目标角度信息,因存在密集多径干扰,导致定位精度低。而本文方法不仅利用了细粒度的相位信息,还通过分集进一步提升了定位精度,当信噪比为-10 dB时,定位误差小于0.4 m。
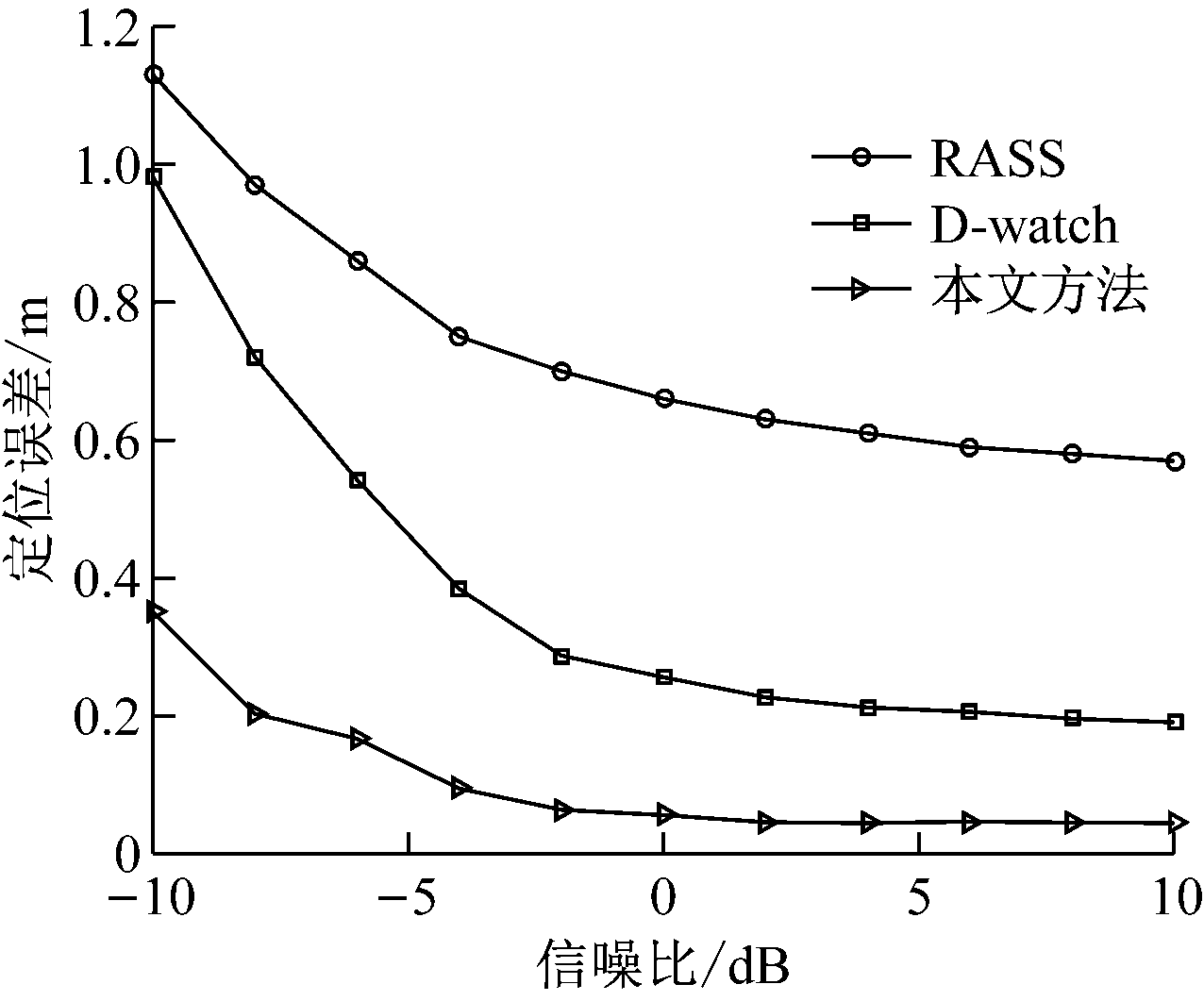
图9 不同方法定位误差对比
Fig.9 Comparison of location errors among different methods
5 结语
采用无源宽带谐波标签建立了矿井无标签目标定位系统,并针对无标签目标提出了空间和频率分集联合的定位方法。仿真结果表明,该方法能够有效解决采样信息不足导致的定位精度低和下行链路多径干扰问题,在低信噪比条件下定位精度可达分米级,满足矿井复杂环境下目标定位需求。
[1] 胡青松,杨维,丁恩杰,等.煤矿应急救援通信技术的现状与趋势[J].通信学报,2019,40(5):163-177.
HU Qingsong,YANG Wei,DING Enjie,et al.State-of-the-art and trend of emergency rescue communication technologies for coal mine[J].Journal on Communications,2019,40(5):163-177.
[2] MINHAS U I,NAQVI L H,QAISAR S,et al.A WSN for monitoring and event reporting in underground mine environments[J].IEEE Systems Journal,2018,12(1):485-496.
[3] HARGRAVE C O,JAMES C A,RALSTON J C.Infrastructure-based localization of automated coal mining equipment[J].International Journal of Coal Science & Technology,2017,4(3):252-261.
[4] LI Jianguo,ZHAN Kai.Intelligent mining technology for an underground metal mine based on unmanned equipment[J].Engineering,2018,4(3):381-391.
[5] 王国法,刘峰,庞义辉,等.煤矿智能化——煤炭工业高质量发展的核心技术支撑[J].煤炭学报,2019,44(2):349-357.
WANG Guofa,LIU Feng,PANG Yihui.Coal mine intellectualization: the core technology of high quality development[J].Journal of China Coal Society,2019,44(2):349-357.
[6] 胡青松,曹灿,吴立新,等.面向矿井目标的双标签高精度定位方法[J].中国矿业大学学报,2017,46(2):437-442.
HU Qingsong,CAO Can,WU Lixin,et al.A dual-tag high precision localization method for coal mine objects[J].Journal of China University of Mining and Technology,2017,46(2):437-442.
[7] 邢智鹏,李春文,陆思聪.基于LQI滤波与联合参数估计的井下人员定位算法[J].煤炭学报,2017,42(6):1628-1633.
XING Zhipeng,LI Chunwen,LU Sicong.Coal mine underground personnel localization algorithm based on LQI filter and joint parameters estimation[J].Journal of China Coal Society,2017,42(6):1628-1633.
[8] 赵彤,李先圣,张雷,等.煤矿井下区间分段视距节点合作定位算法[J].西安电子科技大学学报,2019,46(1):172-179.
ZHAO Tong,LI Xiansheng,ZHANG Lei,et al.Algorithm for cooperational localization of the sectional interval and LOS node in a coal mine[J].Journal of Xidian University,2019,46(1):172-179.
[9] ZHOU Chenming,GRIFFIN J.Phased-based composite ranging for backscatter RF tags: system analysis and measurements[J].IEEE Transactions on Antennas and Propagation,2018,66(8):4202-4212.
[10] 邵小强,李康乐,陈熙,等.基于改进卡尔曼滤波和参数拟合的矿井TOA定位方法[J].煤炭学报,2019,44(5):1616-1624.
SHAO Xiaoqiang,LI Kangle,CHEN Xi,et al,MTOA positioning method of coalmine based on Kalman filter and parameter fitting[J].Journal of China Coal Society,2019,44(5):1616-1624.
[11] 李论,张著洪,丁恩杰,等.基于RSSI的煤矿巷道高精度定位算法研究[J].中国矿业大学学报,2017,46(1):186-194.
LI Lun,ZHANG Zhuhong,DING Enjie,et al.Precision positioning algorithm in coal mine tunnel based on RSSI[J].Journal of China University of Mining and Technology,2017,46(1):186-194.
[12] DING Enjie,LI Xiansheng,ZHAO Tong,et al.A robust passive intrusion detection system with commodity WiFi devices[J].Journal of Sensors,2018:1-12.
[13] 张晓光,孙彦景,霍羽,等.基于TOA/DOA参数估计的隧道高分辨率无源移动目标定位[J].煤炭学报,2018,43(7):1965-1972.
ZHANG Xiaoguang,SUN Yanjing,HUO Yu,et al.Localization of high resolution passive mobile target based on TOA/DOA parameter estimation in tunnel[J].Journal of China Coal Society,2018,43(7):1965-1972.
[14] HAN Jinsong,CHEN Qian,XING Wang,et al.Twins: device-free object tracking using passive tags[J].IEEE/ACM Transactions on Networking,2016,24(3):1605-1617.
[15] TALAMPAS M C R,LOW K S.A geometric filter algorithm for robust device-free localization in wireless networks[J].IEEE Transactions on Industrial Informatics,2017,12(5):1670-1678.
[16] ZHANG Shuai,LIU Kaihua,MA Yongtao,et al.An accurate geometrical multi-target device-free localization method using light sensors[J].IEEE Sensors Journal,2018,18(18):7619-7632.
[17] ZHANG Dian,LIU Yunhuai,GUO Xiaonan,et al.RASS: a real-time,accurate,and scalable system for tracking transceiver-free objects[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(5):996-1008.
[18] 邢天璋,谢彬彬,杨康,等.一种利用无线信号的被动式多目标定位系统[J].西安电子科技大学学报,2018,45(1):93-98.
XING Tianzhang,XIE Binbin,YANG Kang,et al.Passive localization for multi-target via wireless signal processing[J].Journal of Xidian University,2018,45(1):93-98.
[19] YU Fan,LYON K G,KAN E C.A novel passive RFID transponder using harmonic generation of nonlinear transmission lines[J].IEEE Transactions on Microwave Theory and Techniques,2010,58(12):4121-4127.