0 引言
目标定位技术通过参数测量、位置解算、结果优化等步骤确定目标节点的当前位置[1],在工业厂矿、智能交通、居家养老、工业生产、地下空间、军事对抗等领域具有广泛应用。为了实现定位,通常在接收端采用TOA(Time of Arrival,到达时间)、TDOA(Time Difference of Arrival,到达时间差)、AOA(Angle of Arrival,到达角度)或RSSI(Received Signal Strength Indication,接收强度指示)等技术测量接收信号的到达时间、到达时间差、到达角度或信号强度等参数。在进行这些参数测量时,通常假定信号是在信标节点和目标节点之间通过视距(Line-of-Sight,LOS)传播的,即在信标节点和目标节点之间没有障碍物遮挡。
然而,定位场景内通常具有较多障碍物,如矿井环境中存在矿车、巷道壁、矿工等障碍物,且障碍物的位置和运动状态等存在不确定性,使得定位环境更加复杂。障碍物的存在使目标定位不再满足LOS的理想条件,而是经常面临非视距(Non-Line-of-Sight,NLOS)传播的影响,从而引起定位信号的折射、反射、衍射和散射,使得信号传输出现多径效应,导致测距误差增大,进而影响目标定位精度[2]。
因此,减小NLOS传播对定位结果的影响是提高定位精度的重要手段,在目标定位研究中处于非常重要的地位。目前,这方面的研究成果已经比较丰富。本文将对现有NLOS传播文献进行综述,捋清目标定位中的NLOS传播研究脉络和方向,为定位算法设计和定位系统开发提供理论指导。
1 目标定位中的NLOS传播研究体系
1.1 NLOS传播对定位的影响
NLOS传播对定位的影响主要体现在测距阶段[3],它对不同测距方法造成的影响不同。对RSSI定位的影响如图1所示。路径1为没有遮挡时的路径,即LOS路径。路径2为信号通过衍/透射穿过障碍物的传播路径,通过路径2从节点A到达节点B的信号比LOS信号弱。路径3为信号发生折射的传播路径,信号强度比LOS信号弱。从RSSI定位角度而言,更弱的信号强度会误认为收发节点之间比实际距离远,从而降低定位精度。
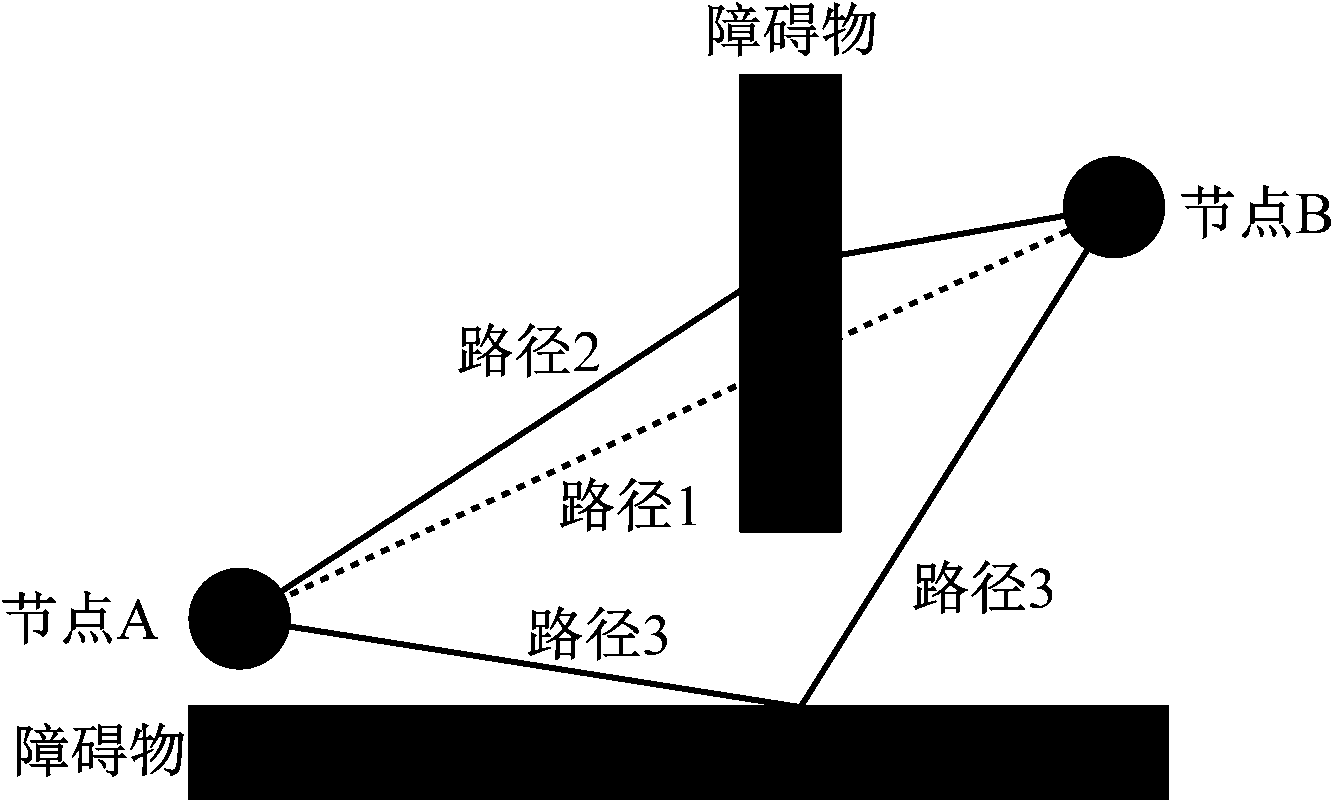
图1 NLOS传播对RSSI定位的影响
Fig.1 Influence of NLOS propagation on RSSI localization
对于AOA定位,NLOS传播将导致到达角度或到达方向发生偏差。以图2为例,信标节点A和信标节点B的位置已知,C为目标节点。假设信号能够穿过障碍物到达信标节点B,由于目标节点C与信标节点B之间有障碍物遮挡,信标节点B测得的信号到达角度由α1变为α2,导致目标节点位置估计误差增大。
当信号不能穿过障碍物时,NLOS传播对AOA定位的影响如图3所示。信标节点B测量的信号到达角度由α1变为α2,发生严重偏差,导致AOA定位算法的位置估计偏差增大,甚至无法进行位置估计。
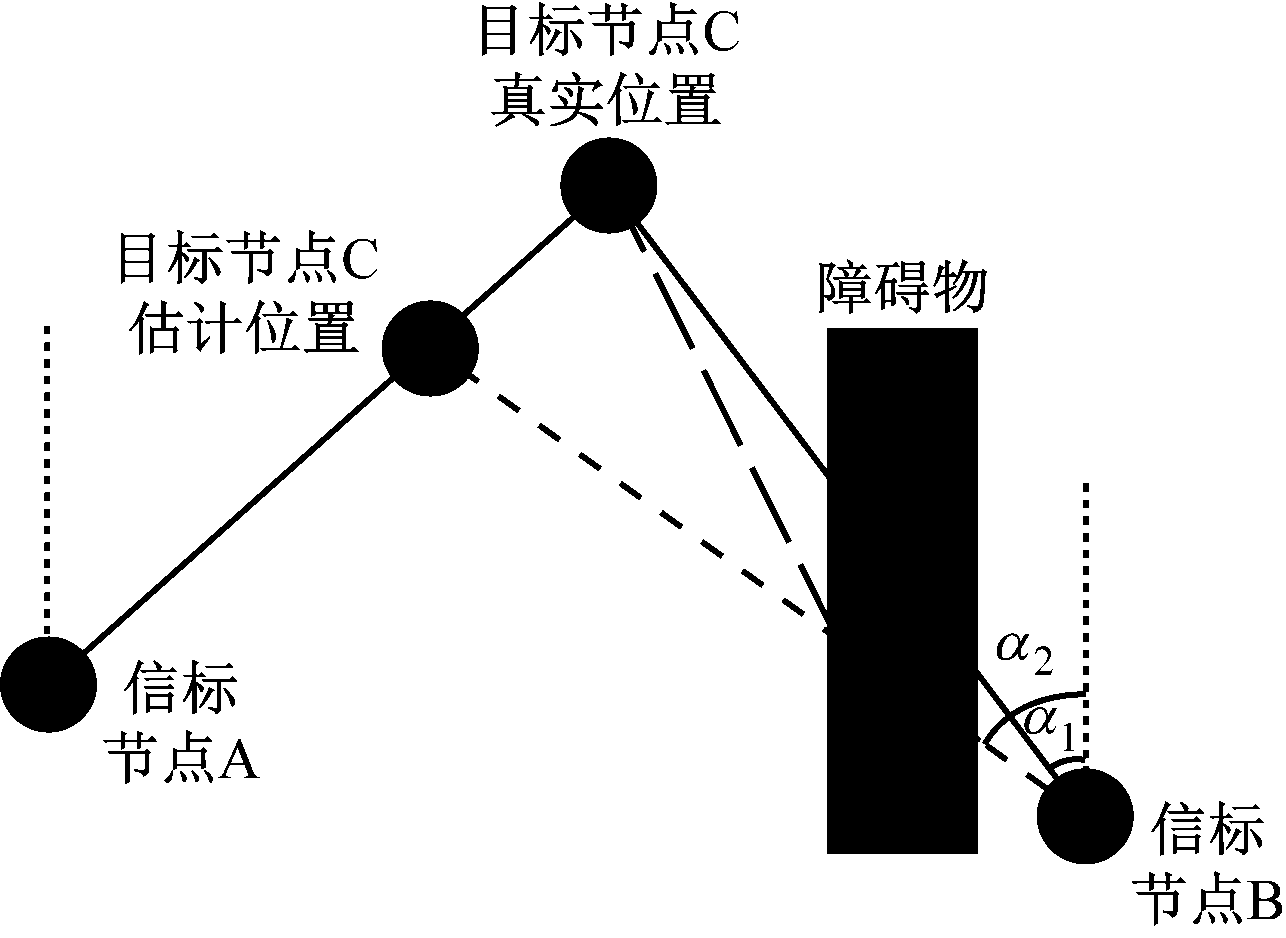
图2 NLOS传播对AOA定位的影响(信号能穿透障碍物时)
Fig.2 Influence of NLOS propagation on AOA localization (signal can penetrate obstacles)
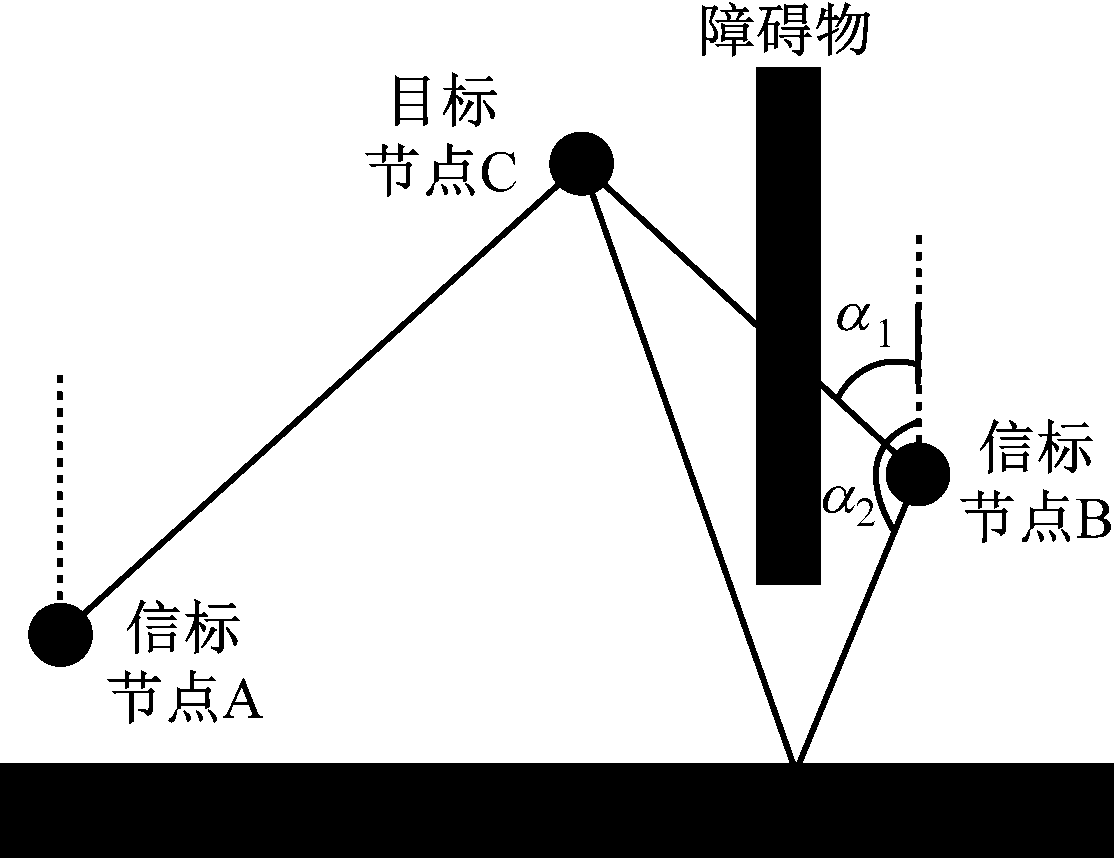
图3 NLOS传播对AOA定位的影响(信号不能穿透障碍物时)
Fig.3 Influence of NLOS propagation on AOA localization (signal cannot penetrate obstacles)
对于TOA和TDOA定位,NLOS传播引起的信号传播路径变化将导致信号传播时间误差。仍以图1为例,路径2和路径3明显长于路径1,因此信号通过路径2和路径3的传播时间大于路径1。若以NLOS信号测得的时间进行目标定位,势必增大TOA或TDOA定位算法的定位误差。
1.2 NLOS传播主要研究方向
目前,目标定位中的NLOS传播研究主要集中在NLOS传播的识别、NLOS传播误差的抑制、NLOS传播的利用及NLOS场景下的定位方法设计4个方面, 如图4所示。
(1) NLOS传播的识别。即判定节点之间是否处于NLOS传播状态,代表性方法有残差检验法[4]、误差统计法[5]、能量检测法[6]、神经网络算法[7]、几何关系法[8-9]。
(2) NLOS传播误差的抑制。旨在抑制NLOS传播误差对定位的影响,主要有基于滤波的方法[10]、基于半参数的方法[11-12]、基于能量检测的方法[13]及基于数据库的方法[14]。这些方法有的可以实时处理,实现动态跟踪,有的则只适合处理离线数据。
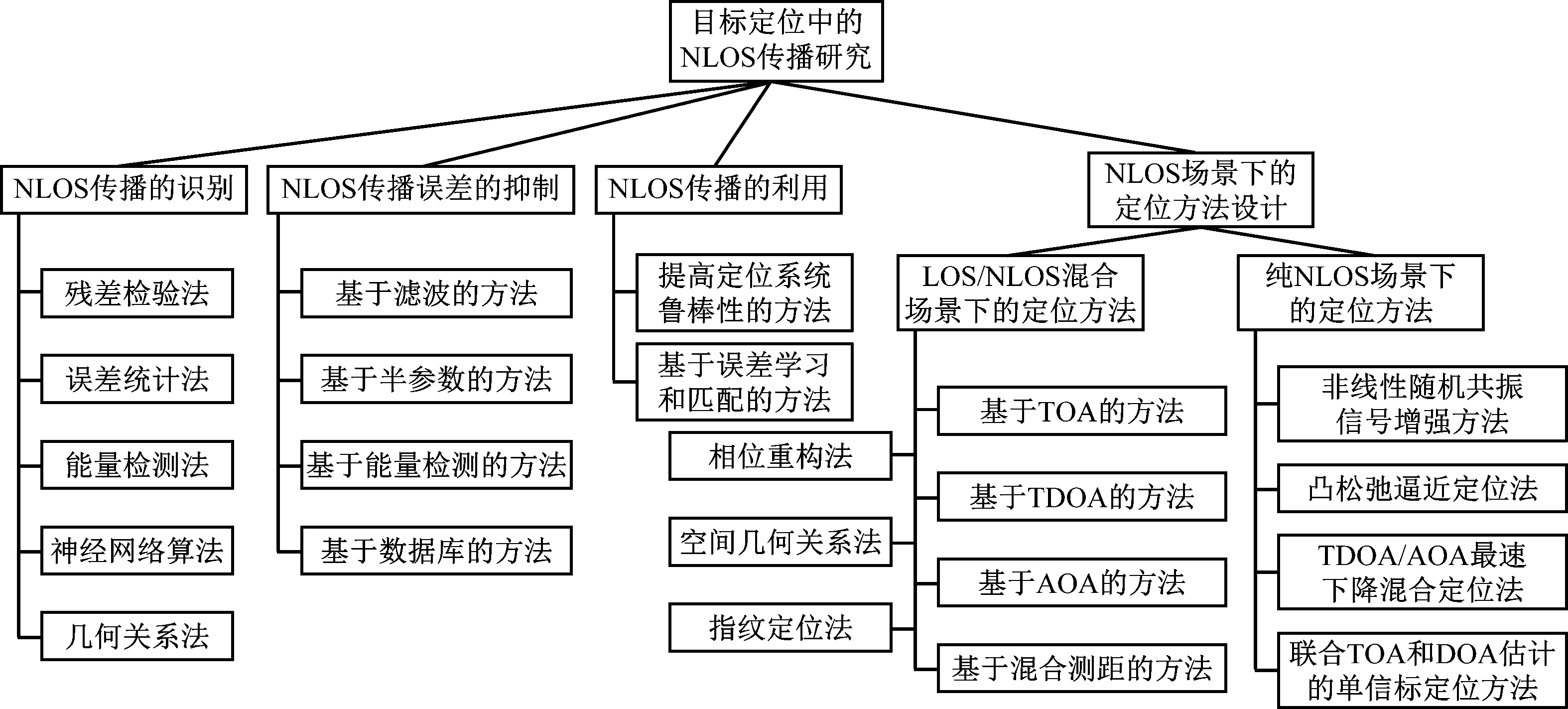
图4 NLOS传播主要研究方向
Fig.4 Main research directions of NLOS propagation
(3) NLOS传播的利用。这类方法反“抑制”之道而行之,通过利用NLOS传播提高NLOS识别率或定位精度,如利用NLOS反射多径信号提高定位系统鲁棒性[15]、基于神经网络提高定位精度[16]等。
(4) NLOS场景下的定位方法设计。主要有2类:① LOS和NLOS混合传播场景(简称混合场景)。该场景虽然有NLOS信号干扰和影响,但仍存在LOS信号。针对TOA[4]、TDOA[17]、AOA[18]、RSSI[19]和混合测距技术,具有相应的定位方法[20],其他还有相位重构法[21]、空间几何关系法[22]、指纹定位法[23]等。 ② 仅有NLOS传播的场景(简称纯NLOS场景)。该场景下完全没有LOS信号,因此只能利用NLOS信号进行目标定位,如结合分布式接收阵列功率谱融合方法的非线性随机共振信号增强方法[24],基于TOA和DOA(Dircection of Arrival, 到达方向)估计虚拟信标节点位置的单信标定位方法[25],将TDOA定位转换为鲁棒性最小二乘法问题的凸松弛逼近定位法[26],以及TDOA/AOA最速下降混合定位法[27]。
下文将按照上述内容体系进行综述。
2 NLOS传播的识别
NLOS传播的识别即判断定位信号发送端和接收端之间是否处于NLOS状态,它是NLOS场景下目标定位的基础。NLOS传播识别方法主要包括残差检验法、误差统计法、能量检测法、神经网络算法和几何关系法。
2.1 残差检验法
Y.T. CHAN等[4]提出了一种残差检验法和德尔塔检验法相结合的NLOS识别方法。该方法以TOA测距信息为数据条件,以2个信标节点为基准,判断第3个信标节点到第N个信标节点中处于LOS传播条件的信标节点。
残差检验步骤如下。
(1) 获取N个信标节点的TOA测距数据。
(2) 通过近似极大似然估计[28]计算位置的估计值。
(3) 计算克拉美罗下界L0及其分布的中心χ2。
(4) 记录中心值大于阈值的信标节点数量l。
(5) 如果满足l≤0.1L0,则维数D=N,维数判定结束;如果不满足,则执行步骤(6)。
(6) 令k=1。
(7) 如果满足N-k=3,则D=3,执行德尔塔检验;如果不满足,构造信标节点集合NCN-k,再执行步骤(2)—(4)。
(8) 如果满足l≤0.1L0,则D=N-k,此时中心值大于阈值的信标节点集合中至少含有D个处于LOS传播的信标节点。如果不满足l≤0.1L0,则令k=k+1,执行步骤(7),直到满足l≤0.1L0。
该方法计算复杂度低,计算速度快,但TOA测距存在误差,且克拉美罗下界本身是一个估计值,使得测量数据是χ2单自由度概率密度函数[29],并不是精确值。该方法只适用于LOS信标节点数量不小于3的情况。
2.2 误差统计法
A. A. Momtaz等[5]提出了一种误差项统计特征算法。误差项包括噪声和NLOS误差,最大特征值的特征向量对应的误差项最大。以此为依据,可对信标节点是否处于NLOS场景进行判断。算法步骤如下。
(1) 获取参数(λ,v,τ)。τ为NLOS误差检测次数。令ρ为高斯白噪声加NLOS误差项,Rρ为ρ的自相关函数,则λ为由Rρ的特征值λi(i=1,2,…,N,N为信标节点数)组成的向量,v为Rρ的最大特征值对应的特征向量。
(2) 通过对特征值进行排序,并将特征值与排序空间对应,得到关于λ的离散函数F。
(1)
(3) 通过概率密度函数(式(2))计算常数α。α用于调整步骤(2)中离散函数F的概率密度符合测距数据。
Fλ(λ)=1-exp(-αλ)
(2)
(4) 通过式(3)计算零均值高斯白噪声的功率上界:
(3)
(5) 如果Γ<λN,则v中最大值为处于NLOS场景的信标节点序号,反之则没有信标节点处于NLOS场景。
该算法的优势在于信标节点数量较大(大于15)情况下,运行时间少,且随着信标节点数量增大,耗时增长缓慢。
2.3 能量检测法
Liang Xiaolin等[6]提出了基于信号能量统计特征的NLOS识别算法。该算法结合来源于一种低复杂度的能量检测器数据,构造基于接收能量块值的最大旋度C和标准差DS的混合参数Q。
Q=CDS
(4)
Q为单调递减的信噪比函数,在4~40 dB内同时包含LOS和NLOS环境。理论上,Q平均值可以用来识别NLOS环境,如式(5)所示。
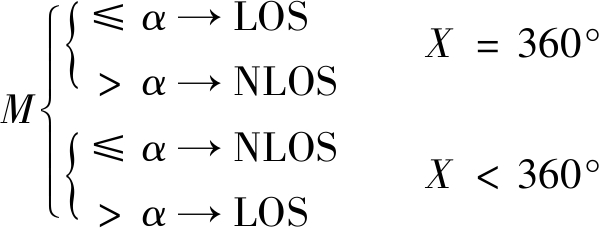
(5)
式中:M为Q平均值;α为识别LOS和NLOS环境的阈值;X为测量所用天线的波束宽度。
该算法在低信噪比时识别精度优势明显,在高信噪比时与基于skewness的算法[30]差距不大,仍具有较高的识别准确率。
2.4 神经网络算法
Zeng Tianyi等[7]提出了一种基于CNN(Convolutional Neural Networks,卷积神经网络)的大规模MIMO(Multiple-Input Multiple-Output,多输入多输出)系统的NLOS识别方法。CNN识别NLOS流程分为离线训练和在线部署2个阶段,如图5所示。离线训练首先利用3D MIMO信道和SRS(Sounding Reference Signals,探测参考信号)序列模拟接收信号,然后进行特征提取,并利用这些特征训练CNN模型。在线部署阶段将接收到的信号进行特征提取,并利用训练好的模型识别LOS/NLOS环境。
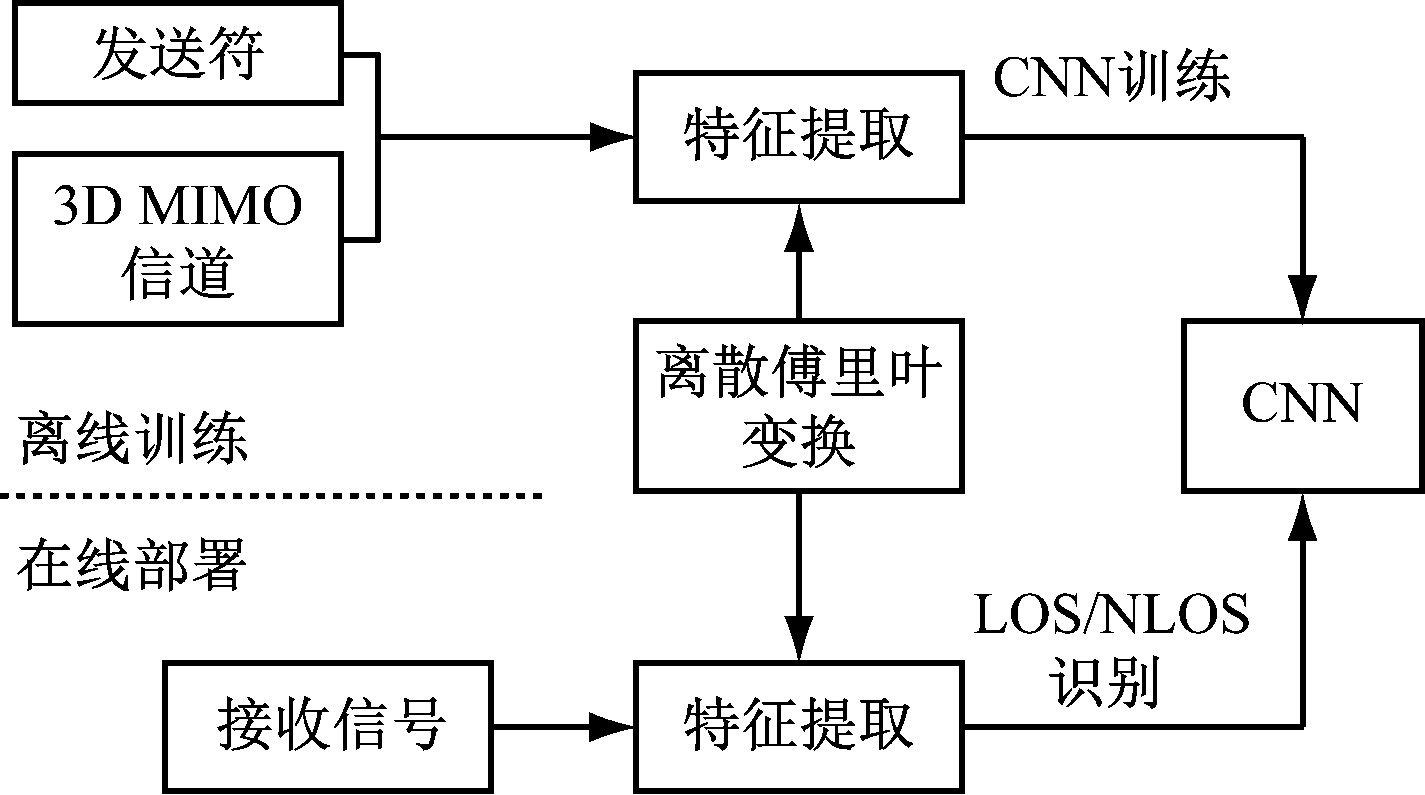
图5 CNN识别NLOS流程
Fig.5 NLOS identification process by CNN
CNN有3个有利于进行底层特征提取矩阵分析的优点,即局部连接、共享权值和池化。由于特征提取矩阵是线性的,如果从分类开始就采用完全连接的其他深度学习技术,将大大增加时间复杂度,而使用局部连接能够减轻时间复杂度。此外,由于空间相邻天线的抽头能量分布具有相似的特性,使用相同的模式共享权值可以较好地提取特征并降低空间复杂度。池化可以减小输入特征映射的维数,具有失真不变性,提高了鲁棒性,减少了处理时间。
该算法的识别错误率低,在低信噪比时增加输出量还可进一步降低错误率;系统中天线越多,算法性能越好;信标节点数量对定位精度影响不大;减小天线间距对定位精度的影响较小。
2.5 几何关系法
Wang Lei等[8]提出了一种稀疏信标节点NLOS环境中非封闭性检查算法。该算法通过检查不同三角形的非封闭性识别NLOS节点,步骤如下。
(1) 获取N个信标节点的坐标及其相应的TOA测距值。
(2) 计算近似估计位置。
(3) 根据近似估计位置分解TOA测距值。
(4) 生成非封闭性检查统计信息。
(5) 进行非封闭性检查。
(6) 如果满足非封闭性条件,则返回步骤(5)进行下一组数据检查,否则将第1个节点和最后一个节点放入欺骗NLOS集合。该步骤仅通过封闭性来识别可能为NLOS测距的节点。
(7) 通过NLOS判别算法从欺骗NLOS集合中准确找出NLOS节点[31]。
非封闭性检查算法的性能不受信标节点几何形状的影响[9],比一致性检验、最小中值平方算法和Geo-n算法精度高。
3 NLOS传播误差的抑制
鉴于NLOS传播对定位精度的巨大影响,人们希望对NLOS传播所引起的误差进行抑制,从而降低或消除NLOS传播对目标定位的影响。本节主要介绍4种NLOS传播误差抑制方法,即基于滤波的方法、基于半参数的方法、基于能量检测的方法及基于数据库的方法。需要注意的是,这些方法很难完全消除NLOS传播误差带来的影响,且面临适用场景、计算复杂度和抑制精度等问题,需要根据具体情况进一步优化,或与其他方法结合使用。
3.1 基于滤波的方法
李奇越等[10]提出了一种基于改进卡尔曼滤波的NLOS误差识别算法。该算法首先建立有色噪声NLOS误差模型,对LOS和NLOS 2种场景的测量数据进行拟合,在此基础上进行基于有色噪声的自适应卡尔曼滤波(图6)。
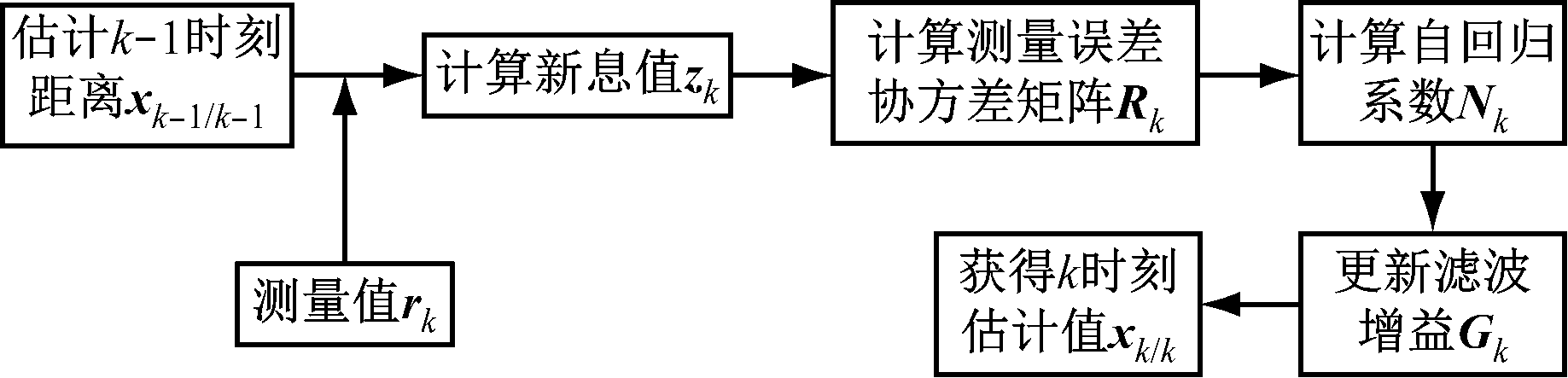
图6 基于有色噪声的自适应卡尔曼滤波流程
Fig.6 Process of self-adaptive Kalman filter based on colored noise
基于有色噪声的自适应卡尔曼滤波步骤如下。
(1) 估计k-1时刻距离向量xk-1/k-1。
(2) 由测量值rk和xk-1/k-1通过式(6)计算新息值zk。
zk=rkAxk/k-1
(6)
式中A为已知常值矩阵。
(3) 由式(7)—式(9)计算测量误差协方差矩阵Rk。
(7)
(8)
Rk=Sk-CPk,k-1CT
(9)
式中:![]() 为i时刻实际新息值的平均值;Pk,k-1为k时刻预测误差协方差矩阵;C为已知常值矩阵。
为i时刻实际新息值的平均值;Pk,k-1为k时刻预测误差协方差矩阵;C为已知常值矩阵。
对式(9)两边取方差得
(10)
式中:γk为零均值高斯白噪声序列矩阵;var(γk)为元素全为γk方差的矩阵;Nk-1为k-1时刻的自回归系数。
(4) 由式(11)计算k-1时刻的自回归系数Nk-1。
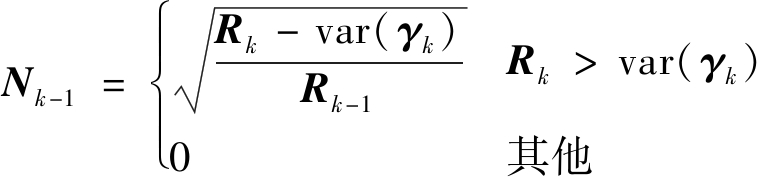
(11)
(5) 计算新的滤波增益Gk。
(6) 计算k时刻的距离估计值xk/k。
相对于自适应卡尔曼滤波和卡尔曼滤波,基于有色噪声的自适应卡尔曼滤波具有对滤波参数的动态调整能力,因此使误差大幅下降。
Wang Yan等[32]提出了基于粒子滤波器的IMU(Inertial Measurement Unit,惯性测量单元)/UWB(Ultra Wide Band,超宽带)融合算法。通过IMU先验信息,提高了每一步的采样精度,使得用更小的粒子数近似真实的后验概率分布,在NLOS环境下得到较高的定位精度。
Cheng Long等[33]提出了一种基于模糊C均值和残差分析的三层混合卡尔曼和无迹卡尔曼滤波的投票算法。该算法采用基于投票的NLOS校正算法和基于模糊C均值的NLOS误差分类算法对测量结果进行处理,抑制了NLOS误差。在此基础上,将NLOS误差分为硬测量和软测量两大类。在NLOS传播严重的环境下,该算法具有较好的鲁棒性和精度。
3.2 基于半参数的方法
H. Ulrich等[11]提出了一种NLOS场景下半参数跟踪和定位方法。在NLOS场景中,极大似然估计法不能将噪声密度体现在位置估计中,只能通过适当调整裁剪参数,在一定程度上调整其形状以适应噪声。为解决极大似然估计算法中位置分数函数鲁棒性不强的问题,该方法使用最初位置估计的残差来计算非参数估计,如采用KDE(Kernel Density Estimate,核心密度估计)生成分数函数估计值。由于在参数模型中使用了非参数的概率密度估计,所以称为半参数方法。残差包含NLOS误差分量,因此残差极有可能是非对称分布,可通过一个非线性、参数化函数对原始残差密度函数进行转换。
Yin Feng等[12]的研究表明:上述方法没有考虑辅助参数与坐标的约束关系;线性化后,测距误差的元素不再是独立同分布;转换原始残差密度函数的非线性、参数化函数缺少参数支撑。鉴此,Yin Feng等[12]提出了一种改进方法,其性能比文献[11]中半参数方法有很大提升。
3.3 基于能量检测的方法
田子建等[13]提出了一种能量检测NLOS传播误差抑制方法。该方法对接收信号进行采样,依据定位时间参数测量值提取特征参量,进而进行NLOS鉴别。
信号采样采用基于能量检测的估计算法,原理是将接收到的信号通过平方器后再进行积分采样,以获得信号的能量采样序列。设积分周期为Tb,则1帧内能量块数为
Nb=Tf/Tb
(12)
式中Tf为帧周期。
则第j帧中,采样序列为
(13)
式中r(t)为能量块。
为使采样序列Yn更趋于统计特征,在多帧内采集能量,即
(14)
将能量采样序列与设定的门限值θ比较,认为第1个超出门限的能量块为DP(Direct Path, 直达路径)所在的能量块,即
(15)
式中:![]() 为DP到达目标节点的时间;
为DP到达目标节点的时间;![]() 为DP所在的能量块。
为DP所在的能量块。
确定了DP所在的能量块后,以DP的检测点为起点截取接收信号,以DP与SP(Strongest Path,最强路径)的相对能量乘积作为NLOS鉴别的参量:
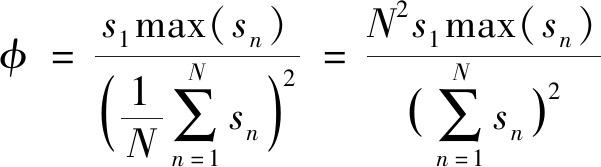
(16)
式中:s1为DP采样序列;sn为截取信号的采样序列;N为截取信号中的能量块数。
当截取信号能量大于鉴别参量时,接收信号为LOS信号,否则为NLOS信号。
3.4 基于数据库的方法
Li Binghao等[14]提出了一种利用数据库修正NLOS误差的移动定位算法。生成数据库原理:假设有几个坐标已知的信标节点,可以直接从这些信标节点中提取NLOS误差,并将其记录到数据库中,生成校正图供在线定位使用。
该算法的缺陷在于尽管测量了一定数量的信标节点,但是并不能覆盖所有区域。另外,为了使数据收集和数据库维护更容易,在收集阶段应尽量减少数据。此外,该算法建立数据库的过程复杂,数据库容量与抑制效果需要权衡,且存在降噪和基准点检测的问题。
4 NLOS传播的利用
目前,NLOS传播利用方法的研究成果不多,下面介绍2种。
M. Hessam等[15]提出了一种利用NLOS的反射多径信号提高定位系统鲁棒性的方法。该方法假定RMC(Reflected Multipath Components,反射多径分量)信息在不同位置的差异能够满足指纹定位分辨的要求,且相同位置的RMC不因时间变化而改变。对RMC信息进行分类的步骤如下。
(1) 特征提取。提取3个特征:从信标节点到目标节点的第1个到达路径所用时间及其接收功率;环境噪声的平均值和标准差;接收信号和预期的序号之间的累积相关关系,用于估计CIR(Channel Impulse Response,信道冲击响应)。
(2) RMC与原始CIR信息过拟合。使用原始的CIR信息作为分类特征。
(3) 将RMC信息模型化。从每个位置的每个RMC特征提取出广义统计特征。
该方法仅用1个信标节点就可在20 cm×20 cm的正方形区域内定位目标,准确率达96%,在鲁棒性和准确性方面都有很大提升。
Wu Shixun等[16]提出了一种基于误差学习和匹配的TOA测量神经网络定位方法。该方法不同于传统的ANN(Artificial Neural Network,人工神经网络)和RBF(Radial Basis Function,径向基函数)神经网络定位方法,是间接获取目标节点的估计位置。该方法整体流程如图7所示,其中![]() (i=1,2,…,M,M为信标节点数)分别为目标节点与第i个信标节点的离线阶段TOA测距值、测距误差及在线阶段TOA测距值。在离线阶段,建立由ANN或RBF神经网络得到的测量距离与误差的非线性地图。在在线阶段,每当获取到信标节点到目标节点的距离时,用训练过的ANN或RBF神经网络得到信标节点的误差信息。从距离测量值中减去误差,即得到调整后的距离测量值,然后利用LLS(Linear Least Square,线性最小二乘)法计算出目标节点位置。
(i=1,2,…,M,M为信标节点数)分别为目标节点与第i个信标节点的离线阶段TOA测距值、测距误差及在线阶段TOA测距值。在离线阶段,建立由ANN或RBF神经网络得到的测量距离与误差的非线性地图。在在线阶段,每当获取到信标节点到目标节点的距离时,用训练过的ANN或RBF神经网络得到信标节点的误差信息。从距离测量值中减去误差,即得到调整后的距离测量值,然后利用LLS(Linear Least Square,线性最小二乘)法计算出目标节点位置。
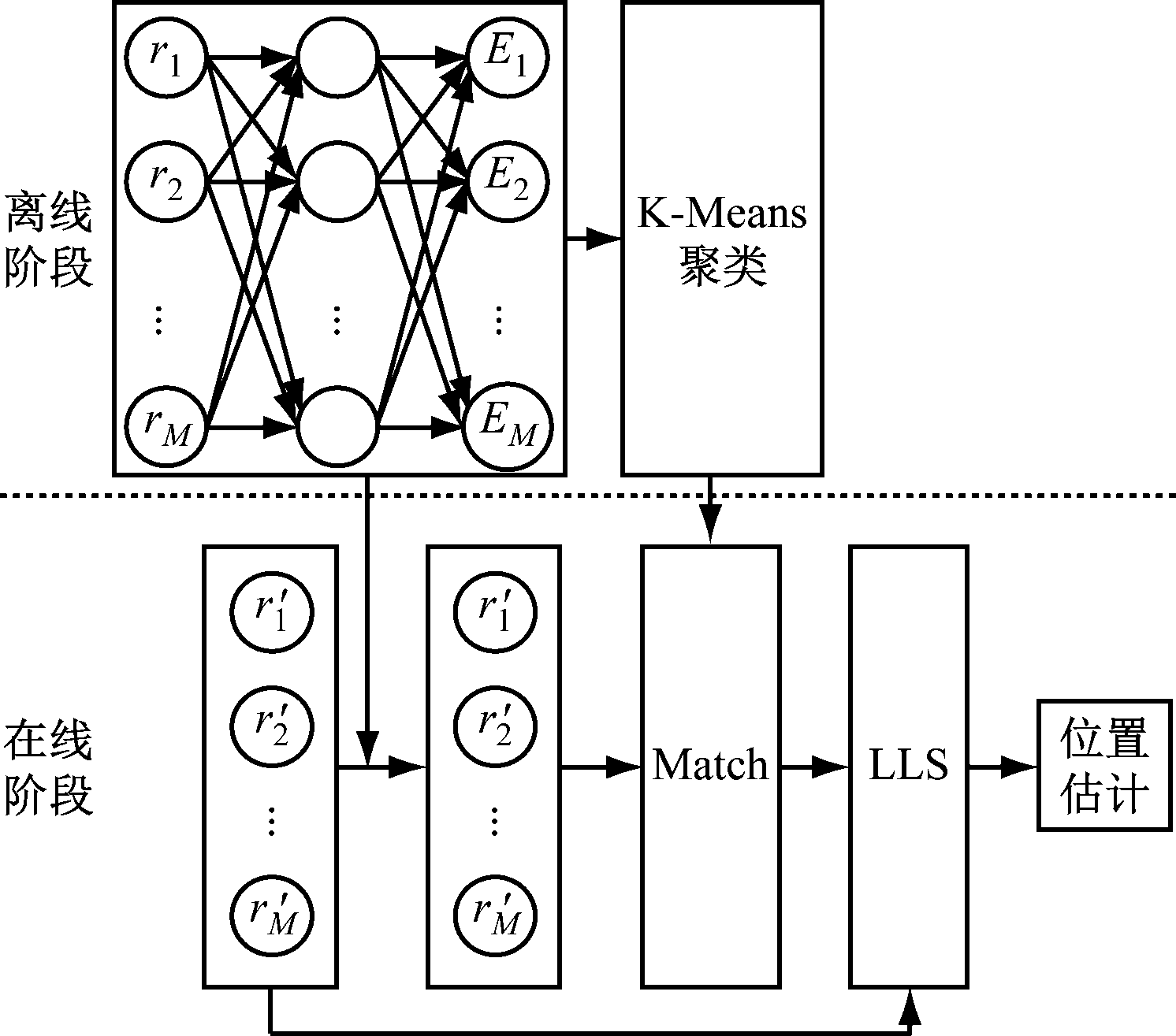
图7 基于ANN/RBF+Match+LLS的定位方法
Fig.7 Localization method based on ANN/RBF+Match+LLS
该算法使用了ANN/RBF+Match+LLS算法,即使在样本不足时也可表现出较高的定位精度。
5 NLOS与LOS混合场景下的定位方法设计
进行NLOS误差的识别、抑制或利用等研究的目的是为了提高目标定位的精度。通常而言,实际应用中基本没有完全理想的纯LOS定位场景,多数时候是LOS信号和NLOS信号并存,部分场景甚至只有NLOS信号。本节综述NLOS和LOS混合场景下的定位方法,第6节探讨纯NLOS场景下的目标定位方法。
NLOS和LOS混合场景下的定位方法主要有基于TOA、基于TDOA、基于AOA、基于RSSI、基于混合测距的方法,以及相位重构法、空间几何关系法、指纹定位法等。
5.1 基于TOA的方法
A. S. Zohair等[34]提出了一种两段封闭式估计方法。首先利用一个距离相关的偏差模型推导出一个距离估计值,然后使用三边定位法进行定位。NLOS场景距离估计结果为
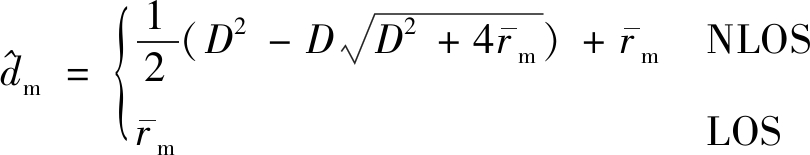
(17)
式中:D=cTμz,当D=0时,NLOS估计变成LOS估计;c为光速;T为距离为1 km时信号传播时延;μz为从信标节点到目标节点间,信号受NLOS影响的对数正态随机变量的概率密度函数均值;![]() 为TOA测距均值。
为TOA测距均值。
该方法只研究了城市环境中的距离偏差模型,其他环境中的模型有待研究。另外,该算法只对3个信标节点的情况进行了研究,更多信标节点的情况需要进一步探讨。
5.2 基于TDOA的方法
Cong Li等[17]提出了一种针对TDOA的NLOS误差修正定位算法。该算法在TDOA残差基础上进行最大似然估计,并将NLOS误差分为3类:确定性NLOS误差;服从高斯分布的NLOS误差;其他NLOS误差。
NLOS误差取决于传播环境,并随时间变化而变化。但是在一个特定时刻,NLOS误差可以视为一个常量。当有足够数量的信标节点可以用来确定目标节点位置时,就可以估计NLOS误差。TDOA双曲线方程可以写为一组未知数为估计坐标和NLOS误差的非线性方程,当NLOS误差为常数时,可通过泰勒级数线性化或两步最小二乘法求解。
如果将NLOS误差作为随机变量,可以使用高斯分布来描述这个模型,用极大似然估计法来计算估计位置。
对于具有已知分布的非高斯NLOS误差,可以推导出一个极大似然位置估计,并使用数值方法来解决最大化问题。
该算法的特点是在信标节点数较少或信标节点几何布局不理想时,修正效果较好。
5.3 基于AOA的方法
毛永毅等[18]提出了一种NLOS传播环境下的AOA定位跟踪算法。在NLOS传播环境下,各信标节点接收的目标节点信号是到达时间不同、到达角度各异的多径信号。在宏蜂窝环境中,由GBSBCM(Geometrically Based Single-Bounced Circle Model,单次反射椭圆模型)可知,多径导致的角度扩展不大于最大角度扩展,为NLOS引起的角度误差限定了范围,进而提高了算法精度。
该算法首先利用RBF神经网络对AOA测距数据进行修正,再利用最小二乘法进行定位,配合相关检测距离门对目标节点进行跟踪。定位步骤如下。
(1) 假定测得K组NLOS环境下的AOA数据,建立用于修正NLOS误差的RBF神经网络,以目标节点不含NLOS误差的AOA测距数据为目标样本矢量对网络进行训练。
(2) 用训练好的RBF神经网络对模拟的AOA测距数据进行修正。
(3) 将修正后的AOA测距数据采用最小二乘法进行位置估算。
该算法使静态定位和动态跟踪性能都得到了有效提高。
5.4 基于RSSI的方法
吴晓平等[19]提出了一种基于RSSI定位模型的NLOS定位算法。该算法分为以下3种情况进行计算。
(1) 当信号强度统计量信息未知时,通过最小化平方残差法,以最小化信号强度测量值与理论值之差计算目标节点坐标。该函数为非线性最小平方优化问题,优化可采用LM(Levenberg-Marquarat)算法。
(2) 当信标节点位置正确且信号强度统计量信息已知时,采用经典的最大似然估计法计算目标节点坐标。
(3) 当信标节点位置存在误差且信号强度统计量信息![]() 已知时,假设信标节点i坐标xi=[xiyi]T,其误差分量Δxi=[ΔxiΔyi]T,Δxi,Δyi分别服从方差为
已知时,假设信标节点i坐标xi=[xiyi]T,其误差分量Δxi=[ΔxiΔyi]T,Δxi,Δyi分别服从方差为![]() 的高斯分布,即
的高斯分布,即![]()
节点间RSSI测距服从的对数衰减模型f(x,xi)对信标节点i坐标xi求导,得
(18)
将因信标节点i位置不确定引起的等效信号强度差记为ηi,显然ηi均值为0,方差为
(19)
式(19)中![]() 由此可推断当信标节点位置存在误差时,以最大似然估计法定位目标位置时,权重系数为
由此可推断当信标节点位置存在误差时,以最大似然估计法定位目标位置时,权重系数为
(20)
当信标节点位置存在误差时,以式(20)计算的权重系数合理权衡了在不同信标节点上的信号强度误差。
5.5 基于混合测距的方法
温良[35]提出了一种基于NLOS鉴别的井下精确定位算法。该算法鉴别NLOS的依据为RSSI算法对NLOS条件的敏感性高于TOF(Time of Flight,飞行时间)算法,即同样的NLOS环境对RSSI算法造成的测距误差高于对TOF算法造成的误差。在进行定位时,获取定位矫正参数分为以下3种NLOS条件进行处理。
(1) 判定目标节点仅一侧存在障碍物。目标节点发射的电磁波信号被障碍物阻挡,信标节点最先收到的是电磁波通过最短巷道壁反射路径到达的信号。由于巷道狭窄,电磁波经过最短反射路径的传输时间与经LOS直线传输的时间不随障碍物与目标节点之间距离不同而大幅变化,所以在判断某一侧存在障碍物后,可根据经验值,使用统一的矫正参数对测距值进行矫正。
(2) 判定目标节点两侧均存在障碍物或均不存在障碍物。由于井下造成NLOS条件的障碍物多为带有目标节点的动目标,所以可根据当前信标节点读取到的目标节点数量来判断该目标节点前后两侧有无障碍物:如果当前信标节点读到目标节点的数量较大,可判定目标节点两侧均存在障碍物,并根据矫正参数对测距值进行矫正;如果当前信标节点读到的目标节点数量较小,则判定目标节点前后两侧均处于LOS环境。
(3) 只能判定目标节点位于信标节点较近位置。由于目标节点位于信标节点较近位置的情况较少,文中没有做过多处理。
该算法的精度在大多数情况下小于3 m,优势在于数据处理过程简单,实用性强。
黄越洋等[20]提出了一种基于TDOA和RSS(Received Signal Strength,接收信号强度)的可行域粒子滤波NLOS定位算法,流程如下。
(1) t=0时刻,初始化必要参数,设置粒子初始权值ωi(0)=1/N,i=1,2,…,N,N为粒子总数,默认值为100。
(2) t≥1时进行NLOS识别,判断每个信标节点和目标节点的LOS状态。
(3) 预测粒子位置。
(4) 计算粒子观测似然并更新粒子权值。
(5) 计算目标节点的位置。
(6) 如果必要,进行重采样。
通过上述步骤即可得出t时刻目标节点位置。
该算法定位精度比普通的粒子滤波算法、仅采用RSSI测距模型的粒子滤波算法及最小二乘法均有大幅提高,并具有较好的鲁棒性。
5.6 相位重构法
Ma Yongtao等[21]提出了一种加权迭代相位重构定位算法,利用在NLOS环境中测量的相位差具有正偏差的特性来定位目标节点。算法定位过程如下。
(1) 基于RFID(Radio Frequency Identification,射频识别)信标估算目标节点的临时位置,利用WLACO(Weighted Localization Algorithm Based on Convex Optimization,基于凸优化的加权定位算法)计算目标节点的相位差。
(2) 计算基本相位偏差。
(3) 计算每个信标由NLOS造成的相位偏差。
(4) 对步骤(3)计算出的相位偏差进行重构。
(5) 将加权值加入WLACO算法。
(6) 重复步骤(1)—(5),直到估计出所有目标节点的位置。
该算法在NLOS环境下的定位精度有显著提升,定位性能较优。
5.7 空间几何关系法
贾骏超[22]提出了一种UWB室内定位的NLOS误差抑制定位算法。该算法基于几何关系推导而来,可根据计算公式经过一步计算得到位置,在实际应用中使用3个信标节点即可求出目标节点的三维坐标。
假设环境中有n个信标节点,坐标为Pi=(xi,yi,zi)(i=1,2,…,n),目标节点坐标为A=(x,y,z)。设ri为待测的目标节点与第i个信标节点之间距离测量值。选定3个信标节点坐标P1,P2,P3建立坐标系,如图8所示。
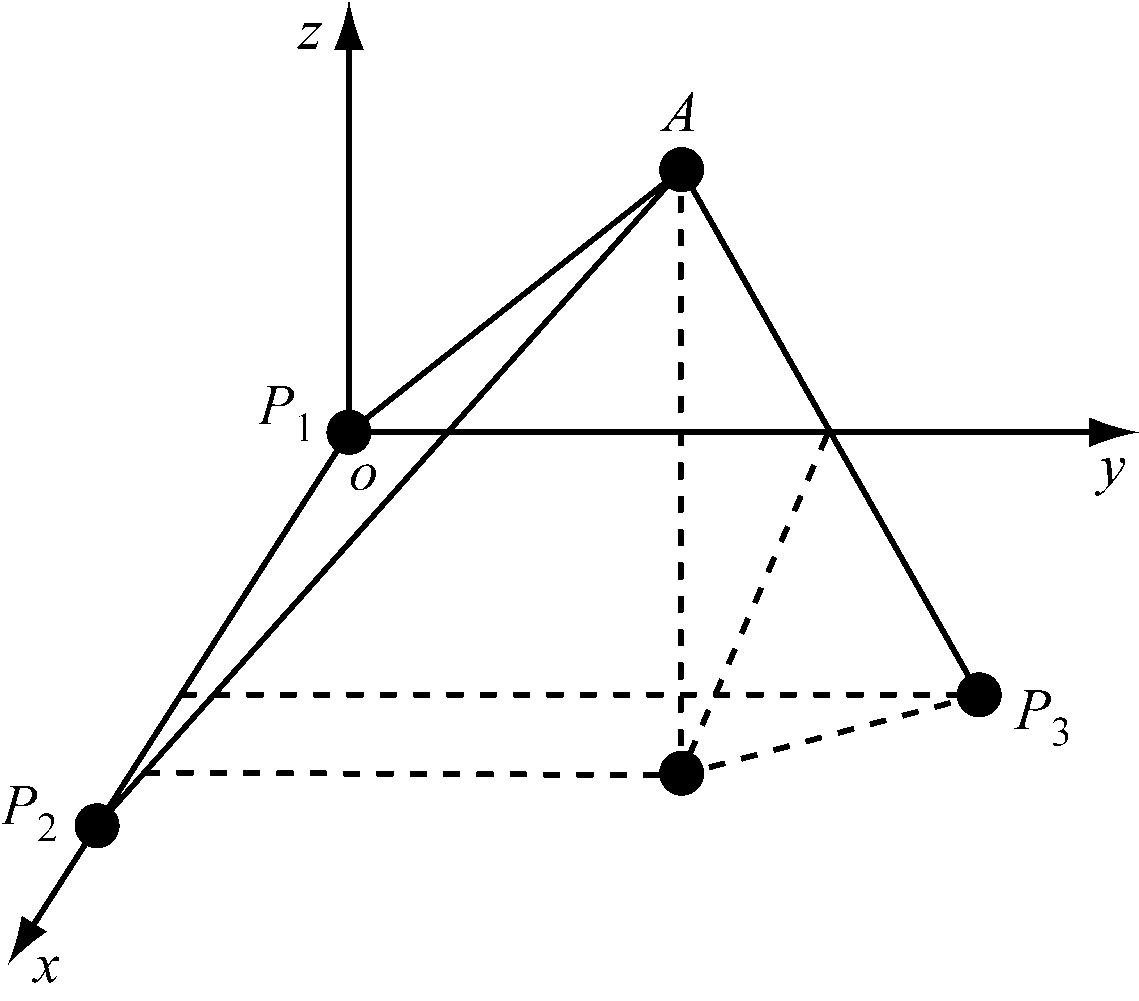
图8 由选定的信标节点建立的坐标系
Fig.8 Coordinate system established by the selected beacon nodes
由几何关系可得
(21)
(22)
(23)
(24)
式中:ex为![]() 方向上的单位向量;s1为
方向上的单位向量;s1为![]() 在ex方向上的长度;ey为
在ex方向上的长度;ey为![]() 方向上的单位向量; s2为
方向上的单位向量; s2为![]() 在ey方向上的长度。
在ey方向上的长度。
由此可得目标节点在图8所示坐标系下的坐标(x′,y′,z′)。
(25)
y′=![]()
(26)
(27)
将图8所示坐标系下的坐标转换到原始坐标系,可得目标节点在原始坐标系下的坐标:
(28)
该算法可以明显减小NLOS传播误差,获得较贴近实际的运动轨迹。
5.8 指纹定位法
王妙羽等[23]提出了一种基于CSI(Channel State Information,信道状态信息)NLOS识别的被动式指纹室内定位方法,包括数据预处理、训练和在线阶段。由于采集到的CSI数据在传输过程中会受到环境噪声干扰,同时由于硬件限制等原因会产生相位偏移,所以需要对CSI数据进行预处理。该方法只利用CSI数据的相位信息,用线性拟合方法对提取到的相位信息进行校正。
训练阶段即离线阶段,分别采集LOS和NLOS位置的CSI数据,得到每个位置的指纹信息,并添加位置信息,作为指纹样本输入神经网络中进行离线训练,构建特征指纹库。
在在线阶段,将实时采集到的CSI数据进行相位矫正后,输入训练好的神经网络进行匹配识别[36],从而得到目标的位置信息。
6 纯NLOS场景下的定位方法设计
针对仅有NLOS信息和低信噪比的场景,He Di等[24]提出了一种结合分布式接收阵列功率谱融合方法的非线性随机共振信号增强技术。
假设有多个目标节点可以接收来自信标节点的信号,每个目标节点都使用一个接收天线阵列,以便进行基于阵列的信号处理和功率谱分析。为了提高接收信号的信噪比,进行基于SR(Stochastic Resonance,随机共振)的信号功率增强或数据预处理。
每个天线的接收阵列均有一个分布式处理器,用于非线性SR处理,从而实现分布式并行SR处理,如图9所示。通过分析或计算每个接收阵列信号的功率谱,可以得到该组接收阵列的总功率谱,并使用传统的MUSIC(Multiple Signal Classification,多重信号分类)算法进行分析。随着分布式并行SR数量增加,系统的信号增强性能加强。
在收集所有光谱信息的同时,提出了一种融合方法来解决NLOS问题。为减少计算复杂度,直接采用MUSIC算法得到结果的加权平均值,进而得到融合结果,即融合谱可以视为不同位置处天线阵列功率谱的加权求和,对应的空间分集可在多个阵列中消除NLOS问题,从而将全局频谱特性更清晰地呈现出来。
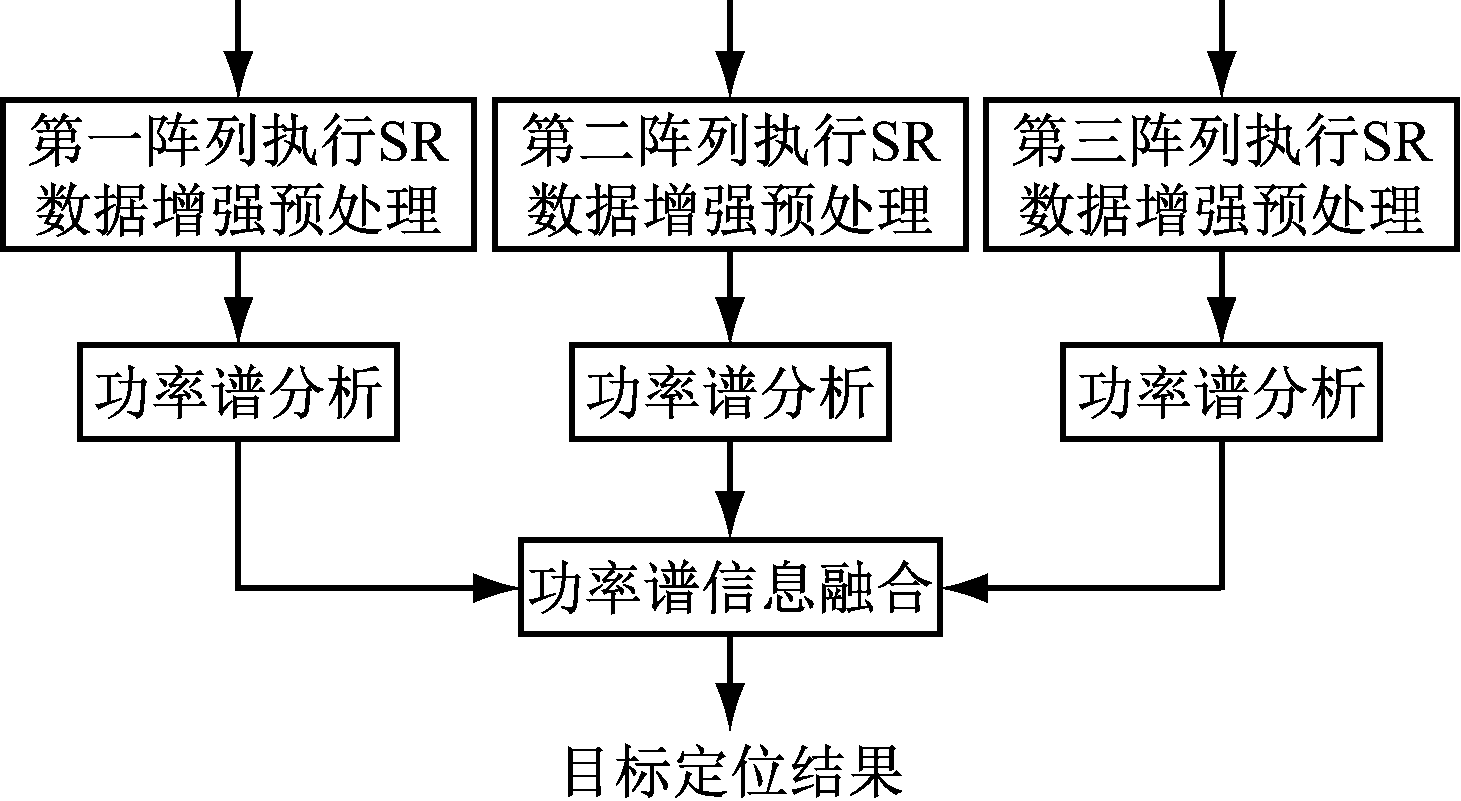
图9 非线性随机共振信号增强技术
Fig.9 Nonlinear stochastic resonance signal enhancement technique
Zhang Rui等[25]提出了一种NLOS环境下基于TOA和DOA估计的单信标定位方法。该方法首先采用联合TOA和DOA估计算法来实现对单个信标节点的位置估计,从接收汉克尔块矩阵中提取参数,以消除多径噪声对信号子空间维数估计的影响。然后,利用反射器的已知平面布置图和TOA/DOA估计值,计算出每一个TOA/DOA估计值在平面布置图中对应的目标节点位置。最后,将该位置与TOA/DOA估计值相结合,使用加权最小二乘法进行位置估计,获得准确的目标节点位置。
在NLOS环境下,特别是数据库点较少的情况下,无论天线单元和信噪比如何变化,该方法都比指纹定位算法精度更高。
Wang Gang等[26]提出了一种NLOS环境下基于TDOA的定位算法。该算法不需要NLOS误差分布或统计信息,而是假设NLOS误差有界。在该假设下,将TDOA定位问题转换为一个鲁棒性最小二乘法问题,由于是非凸的,所以可采用基于凸松弛的逼近方法。该算法在NLOS误差幅度的上界具有较强的鲁棒性。
龚福祥等[27]提出了一种NLOS环境下的TDOA/AOA最速下降混合定位算法。首先介绍TDOA/AOA泰勒级数混合定位算法[37],步骤如下。
(1) 得出TDOA测量值。
(2) 通过TDOA定位算法实现目标函数最优化处理,目标函数定义为TDOA测量值的残差加权平方和。
(3) 得出AOA测量值。
(4) 求出AOA定位算法的目标函数。
(5) 利用TDOA/AOA泰勒级数混合定位算法对TDOA测量值和AOA测量值进行泰勒级数展开,忽略二次以上项,线性化后再采用加权最小二乘算法。然后假设各信标节点获得的测量值的方差相同,设定初始值后进行迭代计算即可得到位置估计值。
TDOA/AOA最速下降混合定位算法在TDOA/AOA泰勒级数混合定位算法的基础上,定义加权最小残差平方和目标函数,各测量值的权值为其方差的倒数。具有NLOS误差的测量值方差大,对目标函数的贡献小,由此抑制了NLOS对定位结果的影响。其中方差可由历史数据测得。然后采用最速下降法求解,设定初始值和合适的步长即可得到不断收敛的位置估计值。
TDOA/AOA最速下降混合定位算法定位精度比TDOA/AOA泰勒级数混合定位算法更高,且对信标节点数的敏感性不强,即当信标节点数变化时,定位精度变化不大。
7 NLOS传播研究的新方向
从定位模型的研究内容看,目前学术界对NLOS的研究无论是从定位的可行性理论、测距技术信息获取手段,还是定位模型计算方式、对定位结果的评估,都已取得了丰硕的研究成果,为定位系统设计者提供了多样化的技术选择。
从定位技术和定位系统的发展来看,对NLOS的研究主要呈现出以下趋势。
(1) 通过多种定位技术的融合降低NLOS的影响,从而提高目标定位精度。
无线定位技术牵涉众多技术或技术组合。为了实现定位,首先要进行信息采集。对于测距定位而言,该信息就是距离信息;对于非测距定位而言,该信息将是节点跳数、邻居节点数量等。不同的技术,其信息采集精度具有很大差别。与此类似,对于不同的无线信号载体、位置解算算法、滤波优化算法等均存在各自的优势和劣势。因此,可将多种技术结合,达到扬长避短的目的,如基于TOA和AOA的联合测距、基于航迹推算与RSSI的联合定位等。
(2) 借助新兴技术提高NLOS场景下的目标定位精度。
无线定位技术的发展历程便是不断吸收新技术提高定位精度和拓展应用领域的历史。从早期发现卫星能够用于定位,到卫星定位技术不断提高,再到卫星定位被广泛应用于各行各业,便是不断借鉴信号处理、空间通信、智能处理、军事技术等新理论和新方法的过程。随后,脱胎于卫星导航定位技术的伪卫星技术被用于室内定位中,而其他技术,如WiFi、蓝牙、UWB等,则催生了一系列新的定位方式。而这些技术的每一次升级也带动了定位精度的提高。目前,以深度学习为代表的人工智能正在无线定位领域,特别是基于视觉的定位领域发挥着越来越大的作用。此外,基于定位结果的轨迹数据分析等应用也如火如荼,新的位置服务正在深刻改变人们的生活。
(3) 通过与其他信息系统的交互引入额外信息,实现跨系统协同定位。
物联网、云计算、大数据使得定位系统越来越成为“大生态”、“大系统”中的一员。以智能煤矿为例,矿井环境是一种典型的NLOS传播广泛存在、多径现象强烈的环境,矿井中的人、机、物、环彼此联系、彼此影响,用于确定人员和物体位置的定位系统可为生产和经营提供决策依据,用于其他目的的物联网节点也可作为定位系统的辅助信标,为抑制NLOS信号提供帮助。
8 结论
(1) NLOS传播对目标定位精度具有重要影响,当前的研究主要集中在NLOS传播识别、NLOS传播误差抑制、NLOS传播利用、NLOS场景下的定位方法设计等方面。
(2) NLOS传播识别是NLOS传播误差抑制和NLOS传播利用的基础,各种研究的最终目的是提高LOS/NLOS混合场景或纯NLOS场景下的定位精度。
(3) 目标定位中的NLOS传播研究需要与测距方法、数据处理技术、目标优化技术、人工智能算法等紧密融合,从多个角度入手,提高NLOS的处理性能。
[1] 胡青松,张申,吴立新,等.矿井动目标定位:挑战、现状与趋势[J].煤炭学报,2016,41(5):1059-1068.
HU Qingsong,ZHANG Shen,WU Lixin,et al.Localization techniques of mobile objects in coal mines:challenges,solutions and trends[J].Journal of China Coal Society,2016,41(5):1059-1068.
[2] 毛科技,邬锦彬,金洪波,等.面向非视距环境的室内定位算法[J].电子学报,2016,44(5):1174-1179.
MAO Keji,WU Jinbin,JIN Hongbo,et al.Indoor localization algorithm for NLOS environment[J].Acta Electronica Sinica,2016,44(5):1174-1179.
[3] GENG Suiyan,KIVINEN J,ZHAO Xiongwen,et al. Millimeter-wave propagation channel characterization for short-range wireless communications[J].IEEE Transactions on Vehicular Technology,2009,58(1):3-13.
[4] CHAN Y T,TSUI W Y,SO H C,et al.Time-of-arrival based localization under NLOS conditions[J].IEEE Transactions on Vehicular Technology,2006,55(1):17-24.
[5] MOMTAZ A A,FEREIDOON B,ROUHOLLAH A,et al.NLOS identification in range-based source localization:statistical approach[J].IEEE Sensors Journal,2018,18(9):3745-3751.
[6] LIANG Xiaolin,JIN Yiheng,ZHANG Hao,et al.NLOS identification and machine learning methods for predicting the outcome of 60 GHz ranging system[J].Chinese Journal of Electronics,2018,27(1):175-182.
[7] ZENG Tianyi,CHANG Yongyu,ZHANG Qi,et al.CNN-based LOS/NLOS identification in 3-D massive MIMO systems[J].IEEE Communications Letters,2018,22(12):2491-2494.
[8] WANG Lei,CHEN Ruizhi,SHEN Lili,et al.NLOS mitigation in sparse anchor environments with the misclosure check algorithm[J].Remote Sensing,2019,11(7):773.
[9] HUA Jingyu,YIN Yejia,WANG Anding,et al.Geometry-based non-line-of-sight error mitigation and localization in wireless communications[J].Science China Information Sciences,2019,62(10).DOI:10.1007/s11432-019-9909-5.
[10] 李奇越,吴忠,黎洁,等.基于改进卡尔曼滤波的NLOS误差消除算法[J].电子测量与仪器学报,2015,29(10):1513-1519.
LI Qiyue,WU Zhong,LI Jie,et al.NLOS error elimination algorithm based on modified Kalman filtering[J].Journal of Electronic Measurement and Instrumentation,2015,29(10):1513-1519.
[11] ULRICH H,ERIC W,ABDELHAKM Z.Robust tracking and geolocation for wireless networks in NLOS environments[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):889-901.
[12] YIN Feng,CARSTEN F,FREDRIK G,et al.TOA-based robust wireless geolocation and Cramér-Rao lower bound analysis in harsh LOS/NLOS environments[J].IEEE Transactions on Signal Processing,2013,61(9):2243-2255.
[13] 田子建,朱元忠,张向阳,等.非视距误差抑制方法在矿井目标定位中的应用[J].工矿自动化,2015,41(6):78-82.
TIAN Zijian,ZHU Yuanzhong,ZHANG Xiangyang,et al.Application of non line-of-sight error suppression method in mine target location[J].Industry and Mine Automation,2015,41(6):78-82.
[14] LI Binghao,DEMPSTER A G,RIZOS C,et al.A database method to mitigate the NLOS error in mobile phone positioning[EB/OL].[2020-03-15].https://wenku.baidu.com/view/90c6752d453610661ed9f4ed.html.
[15] HESSAM M,MILAD H,OMPRAKASH G,et al.UWB-based single-anchor indoor localization using reflected multipath components[C]//International Conference on Computing, Networking and Communications,Honolulu,2019:308-312.
[16] WU Shixun,ZHANG Shengjun,XU Kai,et al.Neural network localization with TOA measurements based on error learning and matching[J].IEEE Access,2019,7:19089-19099.
[17] CONG Li,ZHUANG Weihua.Non-line-of-sight error mitigation in TDOA mobile location[C]//Global Telecommunications Conference,San Antonio,2001:680-684.
[18] 毛永毅,张颖.非视距传播环境下的AOA定位跟踪算法[J].计算机应用,2011,31(2):317-319.
MAO Yongyi,ZHANG Ying.AOA location and tracking algorithm in non-line-of-sight propagation environment[J].Journal of Computer Applications,2011,31(2):317-319.
[19] 吴晓平,陆炳斌,沈浩.基于RSSI定位模型的非视距关系识别方法[J].传感技术学报,2013,26(11):1584-1589.
WU Xiaoping,LU Bingbin,SHEN Hao.NLOS identification approach based on RSSI localization model[J].Chinese Journal of Sensors and Actuators,2013,26(11):1584-1589.
[20] 黄越洋,张嗣瀛,井元伟,等.基于TDOA和RSS的可行域粒子滤波非视距定位算法[J].控制与决策,2017,32(8):1415-1420.
HUANG Yueyang,ZHANG Siying,JING Yuanwei,et al.Non-line of sight localization algorithm based on TDOA and RSS by feasible region particle filter[J].Control and Decision,2017,32(8):1415-1420.
[21] MA Yongtao,ZHOU Liuji,LIU Kaihua,et al.Iterative phase reconstruction and weighted localization algorithm for indoor RFID-based localization in NLOS environment[J].IEEE Sensors Journal,2014,14(2):597-611.
[22] 贾骏超.超宽带室内定位中NLOS误差抑制方法探讨[J].导航定位学报,2017,5(2):60-64.
JIA Junchao.NLOS error mitigation for indoor positioning of ultra-wideband[J].Journal of Navigation and Positioning,2017,5(2):60-64.
[23] 王妙羽,李宪军.基于CSI非视距识别的被动式指纹室内定位[J].无线互联科技,2019,16(3):28-29.
WANG Miaoyu,LI Xianjun.Passive indoor positioning based on CSI NLOS recognition[J].Wireless Internet Technology,2019,16(3):28-29.
[24] HE Di,CHEN Xin,ZOU Danping,et al.A novel wireless positioning approach based on distributed stochastic-resonance-enhanced power spectrum fusion technique[C]//IEEE International Symposium on Circuits and Systems,Sapporo,2019:1-5.
[25] ZHANG Rui,XIA Weiwei,YAN Feng,et al.A single-site positioning method based on TOA and DOA estimation using virtual stations in NLOS environment[J].China Communications,2019,16(2):146-159.
[26] WANG Gang, SO A M C,LI Youming.Robust convex approximation methods for TDOA-based localization under NLOS conditions[J].IEEE Transactions on Signal Processing,2016,64(13):3281-3296.
[27] 龚福祥,王庆,张小国.NLOS环境下无线通信网络中的TDOA/AOA混合定位算法[J].东南大学学报(自然科学版),2010,40(5):905-910.
GONG Fuxiang,WANG Qing,ZHANG Xiaoguo.TDOA/AOA hybrid wireless location algorithm in cellular networks with NLOS condition[J].Journal of Southeast University(Natural Science Edition),2010,40(5):905-910.
[28] CHAN Y T,HANG Y C,CHING P C.Exact and approximate maximum likelihood localization algorithms[J].IEEE Transactions on Vehicular Technology,2006,55(1):10-16.
[29] ZUBOV V I.Random variables and stochastic processes[J].IFAC Proceedings Volumes,2000,33(16):403-414.
[30] LIANG Xiaolin,ZHANG Hao,LU Tingting,et al.Extreme learning machine for 60 GHz millimetre wave positioning[J].IET Communications,2017,11(4):483-489.
[31] CHANG Xiaowen,GUO Ying.Huber's M-estimation in relative GPS positioning: computational aspects[J].Journal of Geodesy,2005,79(6):351-362.
[32] WANG Yan,LI Xin.The IMU/UWB fusion positioning algorithm based on a particle filter[J].ISPRS International Journal of Geo-Information,2017,6(2358).DOI:10.3390/ijgi6080235.
[33] CHENG Long,LI Yifan,WANG Yan,et al.A triple-filter NLOS localization algorithm based on fuzzy C-means for wireless sensor networks[J].Sensor,2019,19(12155).DOI:10.3390/s19051215.
[34] ZOHAIR A S,ZHOU Xiangyun,THRSHARAD A.A novel TOA-based mobile localization technique under mixed LOS/NLOS conditions for cellular networks[J].IEEE Transactions on Vehicular Technology,2016,65(11):8841-8853.
[35] 温良.基于非视距鉴别的井下精确定位技术研究[J].煤炭科学技术,2016,44(7):109-115.
WEN Liang.Study on accurate positioning technology in underground mine based on none line of sight distinguishment[J].Coal Science and Technology,2016,44(7):109-115.
[36] MARCELON D S,REINERS T.Enhanced localization systems with multipath fingerprints and machine learning[J].IEEE Sensors Journal,2019,18(11):1-6.
[37] 毛永毅,李明远,张保军.基于BP神经网络的蜂窝无线定位算法[J].计算机工程与应用,2008,44(3):60-63.
MAO Yongyi,LI Mingyuan,ZHANG Baojun.Cellular localization algorithm based on BP neural network[J].Computer Engineering and Applications,2008,44(3):60-63.