0 引言
常用煤矿机械设备监测监控系统通过设定门限值实现机械设备故障报警,但发生报警时设备已经出现了不同程度的损坏或者性能降低,这种滞后报警给维护、维修工作带来很大的被动性,导致设备存在安全隐患[1]。振动信号能快速响应机械设备的状态变化,且适用的信号处理方法灵活多样,因此振动信号分析法在机械故障诊断中应用最为广泛,张鑫媛[2]、李赟恒[3]、关长江[4]、华伟[5]等对煤矿机械振动信号去噪、特征提取等进行了研究。在一般情况下,通过提取振动信号的特征能够分析出机械设备的运行状态,因此,采用机械振动信号对机械设备状态进行准确的预测有重要意义。通过查阅大量文献,发现目前对机械振动信号预测的研究主要集中在非煤行业[6-8],对煤矿机械振动信号预测的研究较少。针对上述问题,本文提出一种以本征模态函数(Intrinsic Mode Function,IMF)分量为输入特征的基于支持向量机(Support Vector Machine,SVM)的煤矿机械振动信号组合预测方法。首先对振动信号进行经验模态分解(Empirical Mode Decomposition,EMD),将分解之后的IMF分量按照其波动程度分成高频振动序列和低频振动序列两组,并分别重构为高频子序列和低频子序列,然后选择IMF分量为输入特征,采用SVM分别对高频子序列和低频子序列进行预测,最后将二者的预测结果叠加,得到最终预测值。该组合预测方法提高了煤矿机械振动信号预测精度。
1 组合预测方法原理
1.1 EMD
EMD是一种自适应的时频分析方法,它能够把非平稳信号分解成若干IMF分量,各IMF分量分别凸显出原始信号的特定局部特征[9-11]。假定被分析的原始信号为x(t),经过EMD处理,x(t)可表示成不同尺度波动的IMF分量和1个趋势项的组合。
(1)
式中:n为IMF分量个数;cj为IMF分量;r为趋势项。
1.2 预测信号预处理
机械振动信号所包含的不同时间尺度的分量发展趋势有所差异,以滚动体故障的轴承振动信号为例,对其进行EMD处理,结果如图1所示。可看出前2个IMF分量的频率较高,而其他IMF分量及残余分量的频率较低,高频分量和低频分量在变化趋势上存在较大差异。如果直接对信号进行预测,不考虑不同时间尺度的分量发展趋势差异性,会降低预测精度。笔者应用信号处理方法将原始信号分解成不同尺度上的分量再对其进行预测。
图1 滚动体故障的轴承振动信号EMD结果
Fig.1 EMD results of bearing vibration signals of rolling body fault
信号经EMD处理后,得到相对平稳的IMF分量,然而IMF分量个数随着数据的变化并不完全相同,这会加大SVM预测模型建立的难度。为了解决该问题,借鉴文献[12]针对原始数据不同性状部分使用不同方法进行预测的思想,将波动程度相近的IMF分量进行重构,使得预测对象减少,便于预测模型的建立。
2 组合预测方法实现
将波动程度相近的IMF分量进行重构,得到高频子序列和低频子序列,对其分别使用SVM进行预测,然后叠加2个预测结果,形成最终的预测值。组合预测流程如图2所示。
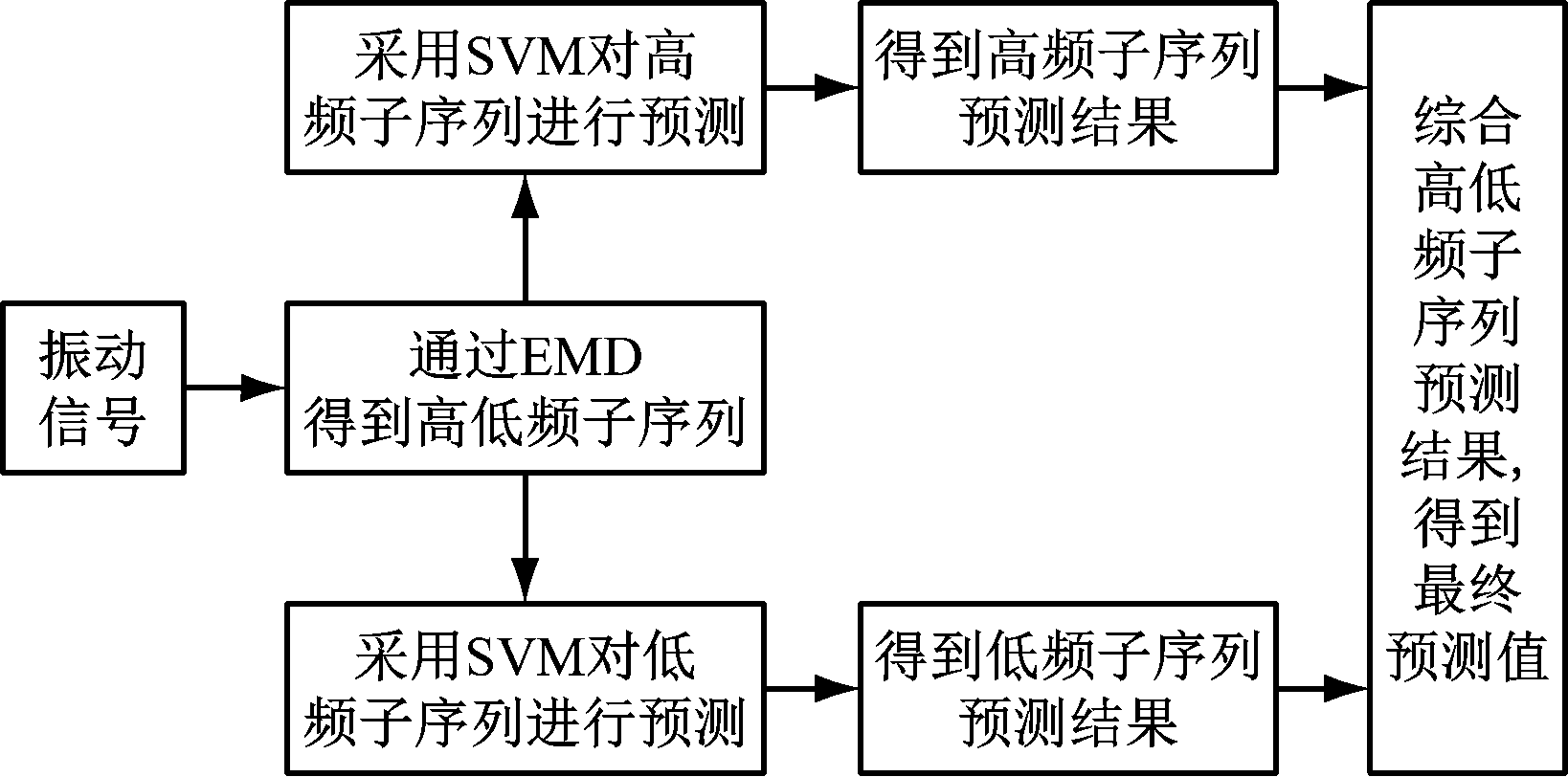
图2 组合预测流程
Fig.2 Combined prediction flow
预测特征的选取对预测结果的影响非常重要,特征选取太多可能会混杂与预测值无关的特征,太少则可能缺失重要特征,造成预测精度降低[13]。文献[13]采用EMD处理后得到的IMF分量作为特征对模型进行训练,在不增加额外测量工作量的情况下,对数据进行扩充,以提高预测精度。
组合预测方法应用于振动信号x(t)的预测步骤如下。
(1)采用EMD将x(t)分解为n个IMF分量和1个趋势项,如式(1)所示。
(2)将频率相对较高的i个IMF分量组成高频子序列h(t),频率相对较低的(n-i)个IMF分量和趋势项组成低频子序列l(t)。
(2)
(3)
(3)以c1,c2,…,ci组成的i维特征向量作为输入特征对SVM预测模型进行训练,并用训练好的模型对h(t)进行预测,得到预测值h*(t)。
(4)以ci+1,ci+2,…,cn及r组成的(n-i+1)维特征向量作为输入特征对SVM预测模型进行训练,并用训练好的模型对l(t)进行预测,得到预测值l*(t)。
(5)将步骤(3)、(4)的预测值进行叠加,得到最终的预测结果c*(t)。
c*(t)=h*(t)+l*(t)
(4)
3 实验验证
3.1 实验数据
选取轴承实验数据进行组合预测方法有效性验证。轴承数据来源于西储大学轴承数据中心。功率为1 470 W的电动机通过轴带动安装在实验台中间位置轴承座上的轴承转动。采用数据记录仪采集轴承振动加速度信号[14]。选取的数据来自电动机驱动端传感器,采样频率为12 kHz。
3.2 预测结果分析
采样210个振动信号,其中前201个采样点作为训练数据,后9个采样点作为测试数据。轴承原始振动信号波形如图3所示,其中g为重力加速度。
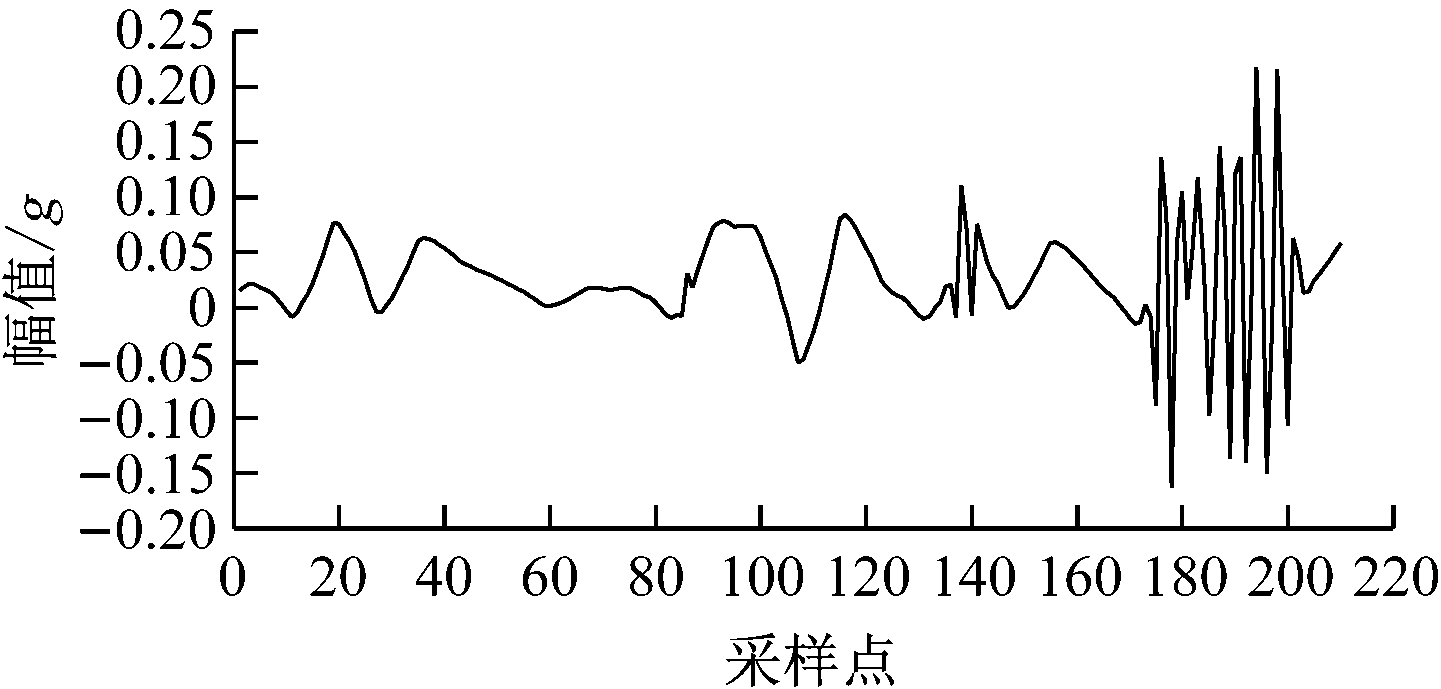
图3 轴承原始振动信号波形
Fig.3 Original vibration signal waveform of bearing
对轴承振动信号进行小波阈值降噪后,对其进行EMD,得到的IMF分量及趋势项如图4所示。
图4 IMF分量及趋势项
Fig.4 IMF components and trend items
将频率相对较高的c1,c2划分为高频子序列,如图5所示,可看出其震荡比较强烈。将高频子序列各采样点信号构造为二维特征对SVM预测模型进行训练,得到高频子序列的9个预测值,如图6所示。
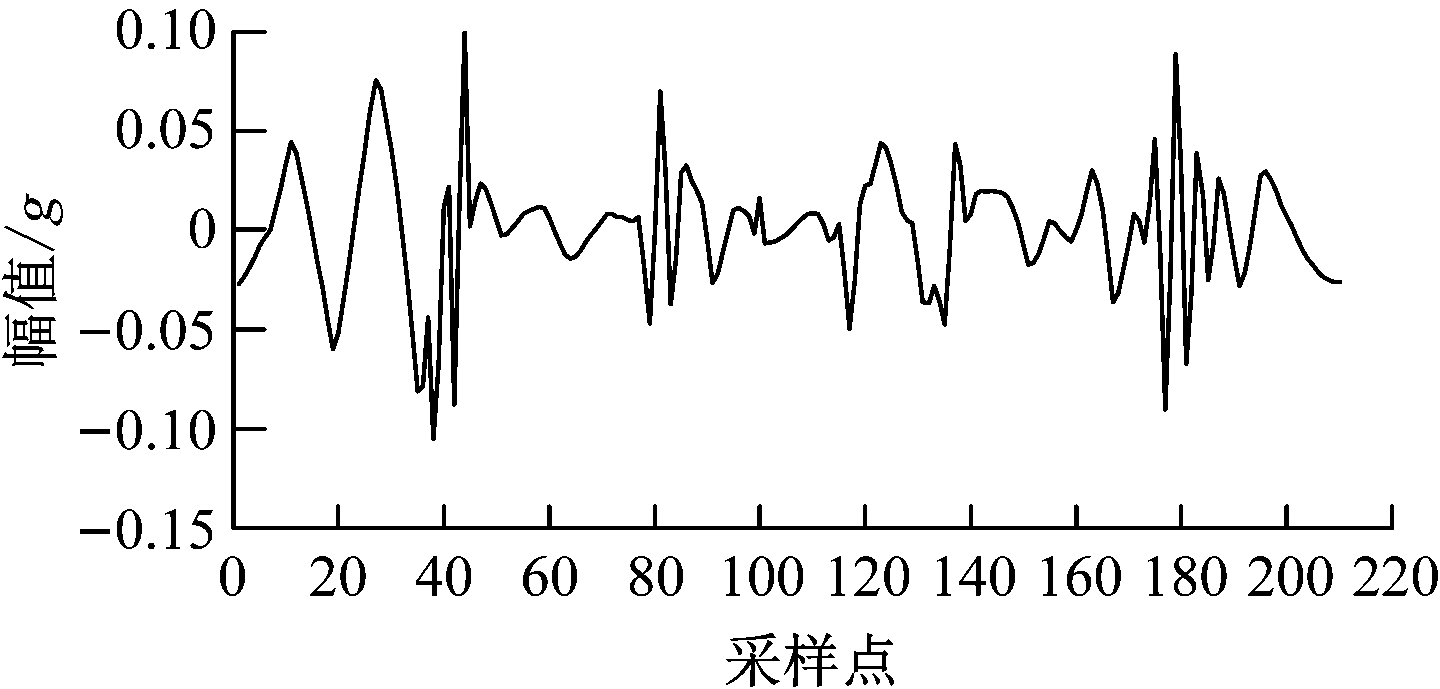
图5 高频子序列
Fig.5 High frequency subsequence
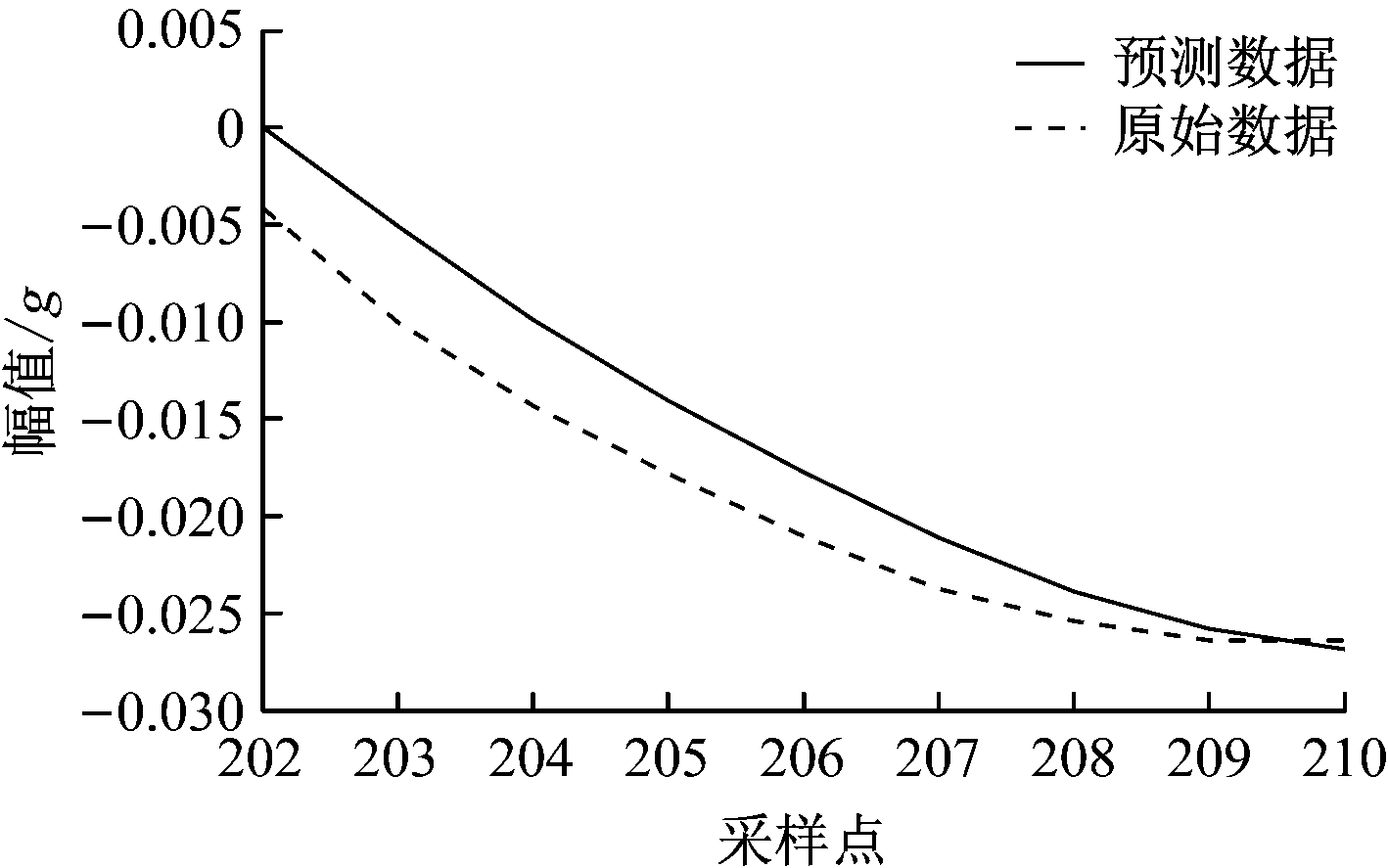
图6 高频子序列预测值
Fig.6 Prediction values of high frequency subsequence
将c3,c4,c5,r划分为低频子序列,如图7所示,可看出其震荡比较缓和。将低频子序列对应的各采样点信号构造为四维特征对SVM预测模型进行训练,得到低频子序列的9个预测值,如图8所示。
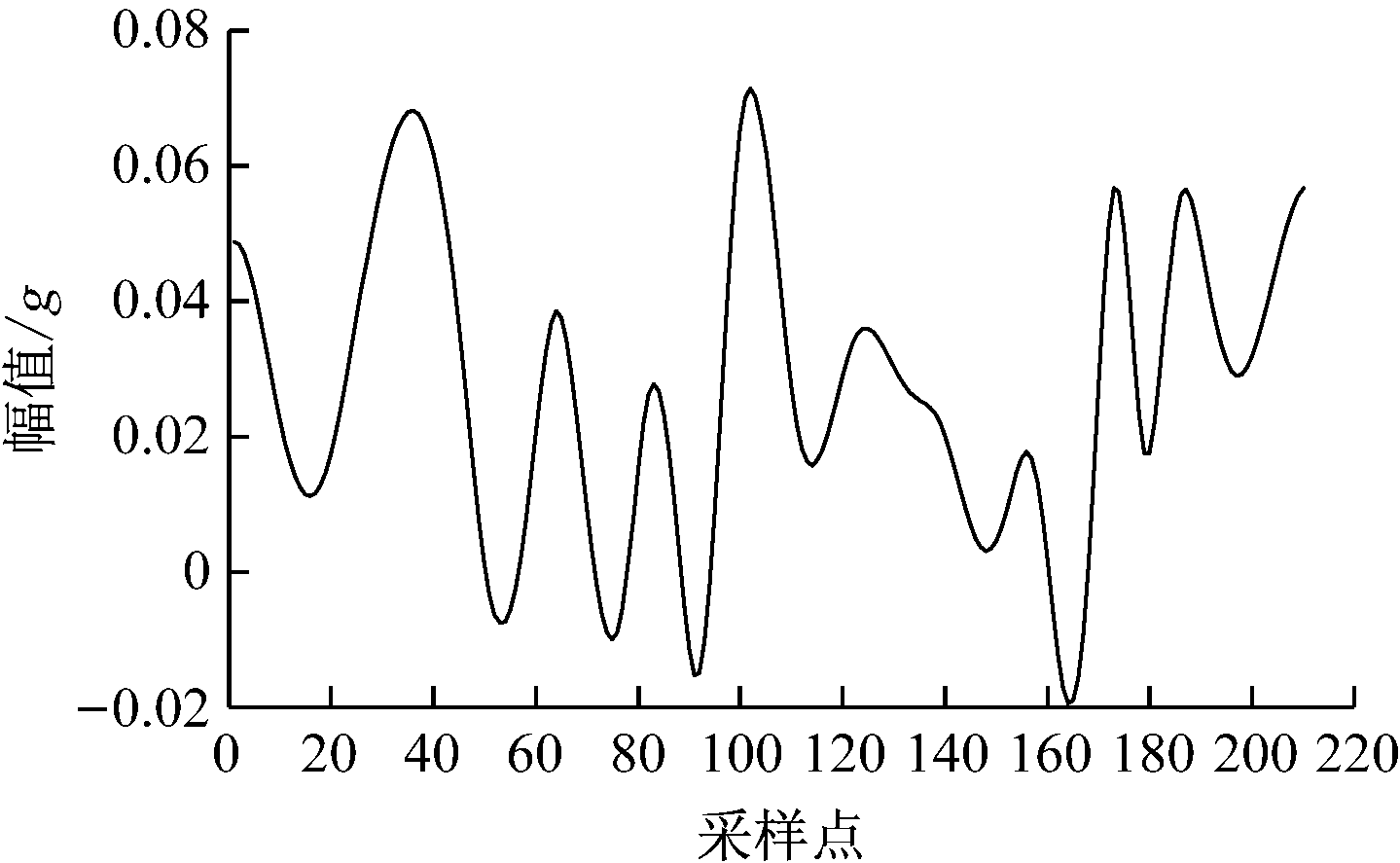
图7 低频子序列
Fig.7 Low frequency subsequence
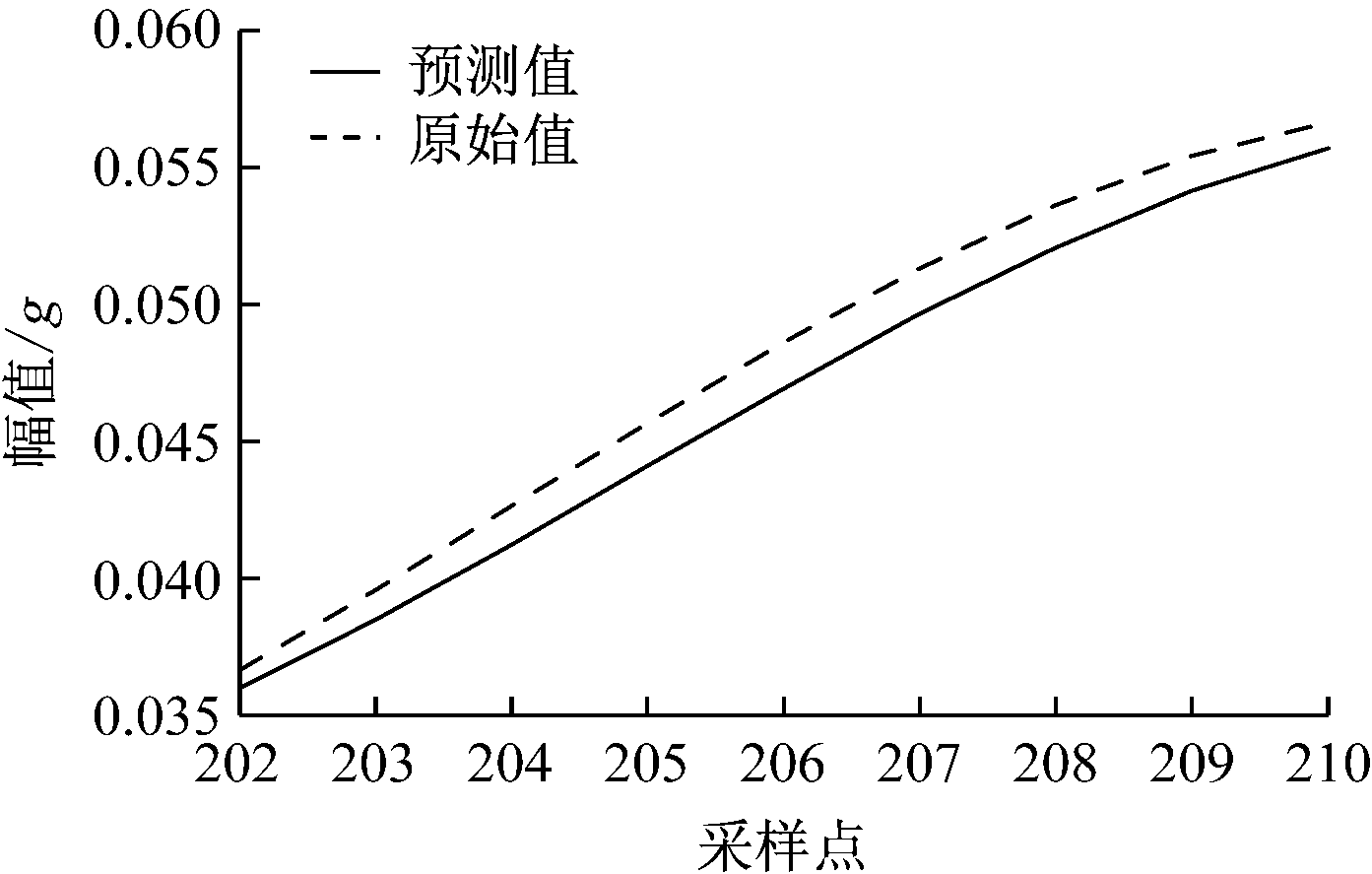
图8 低频子序列预测值
Fig.8 Prediction values of low frequency subsequence
然后将高低频子序列预测值进行叠加,得到轴承振动信号的9个预测值,如图9所示。
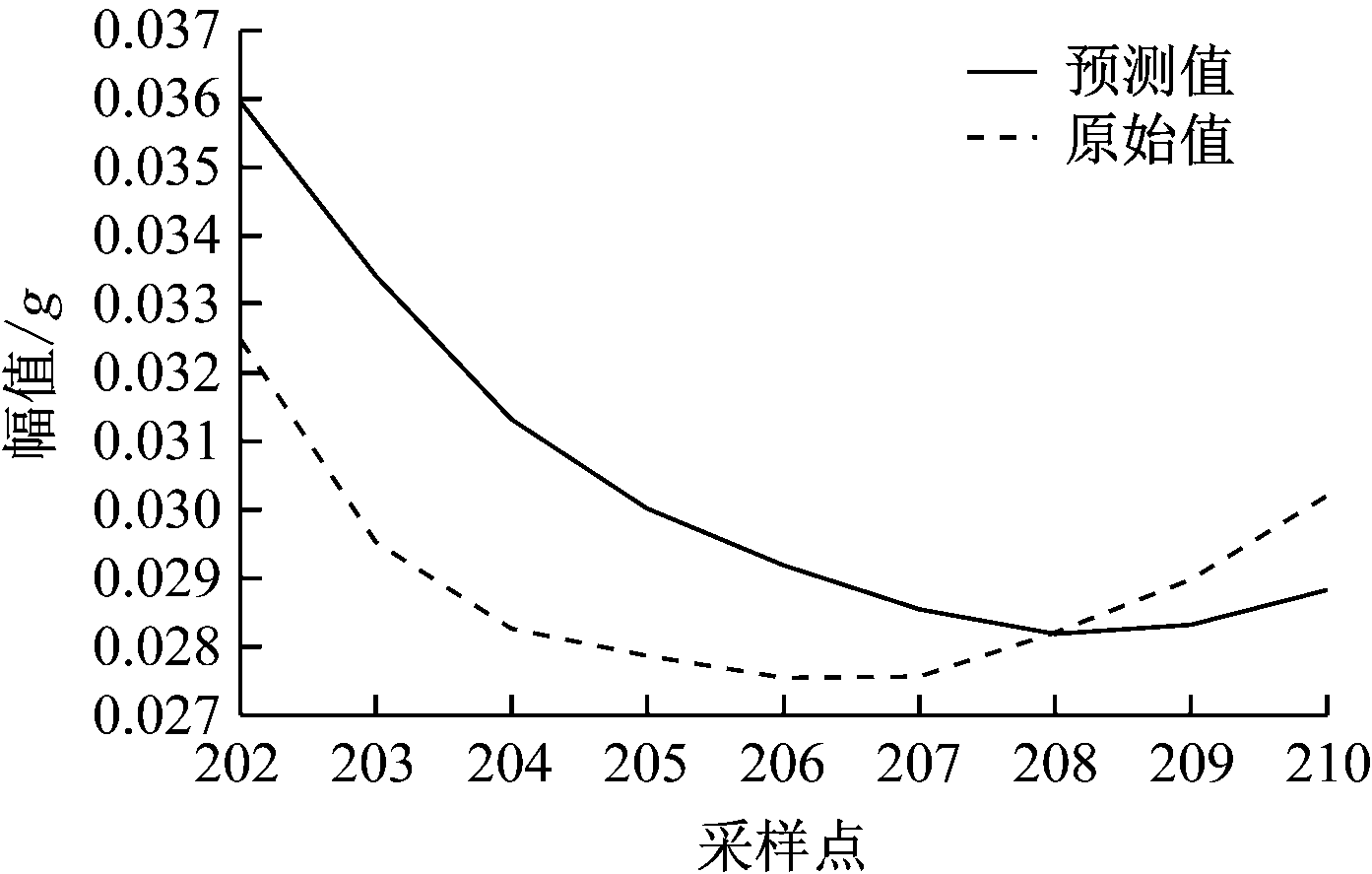
图9 振动信号预测值
Fig.9 Prediction values of vibration signal
为了验证组合预测方法的优越性,采用直接预测方法进行对比,结果如图10所示。直接预测方法是将c1-c5,r对应的各采样点信号构造为六维特征对SVM预测模型进行训练,得到原始振动信号的9个预测值。从图10可看出,组合预测方法的预测值与原始值更接近。
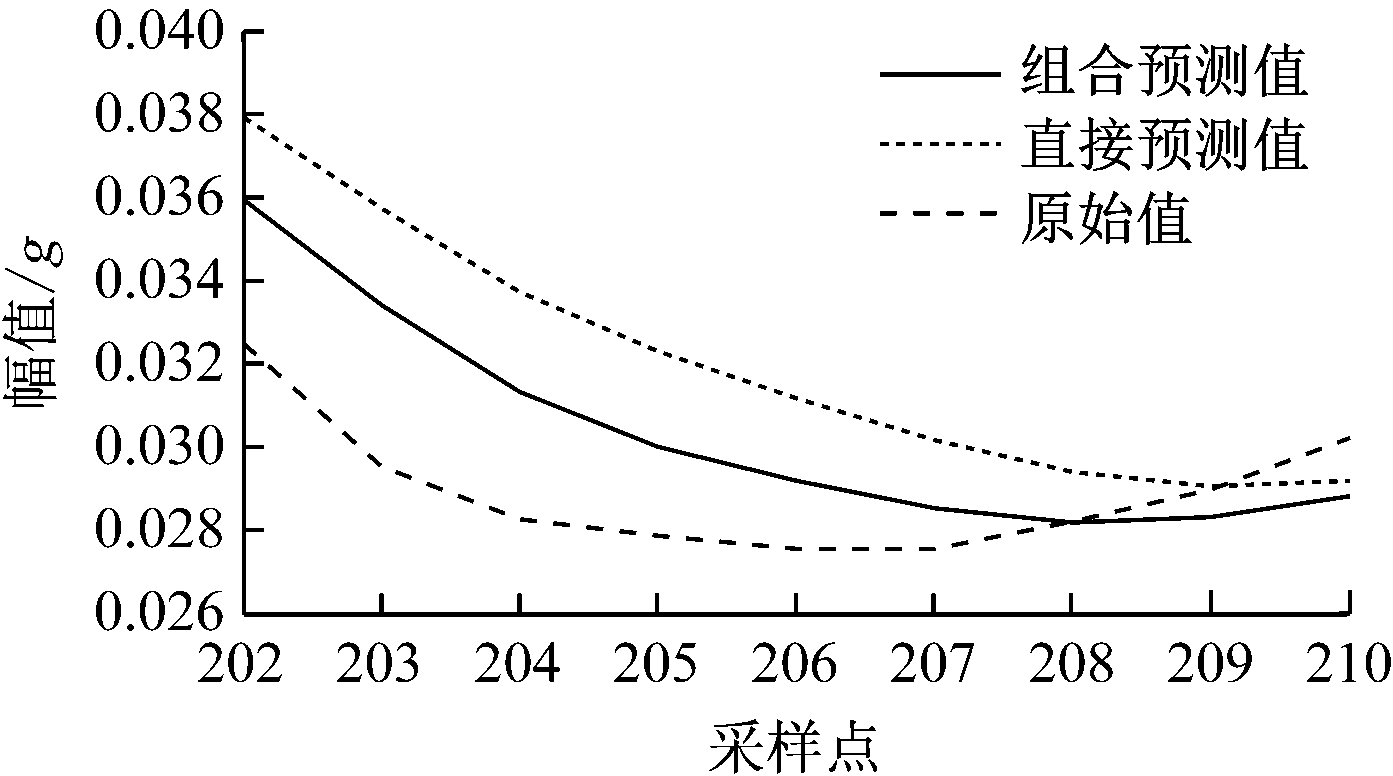
图10 组合预测方法和直接预测方法的预测结果对比
Fig.10 Prediction results comparison of combined prediction method and direct prediction method
选取均方根误差、平均绝对误差及平均绝对百分比误差3个指标,对2种预测方法的预测精确度进行比较,结果见表1。可看出组合预测方法的均方根误差、平均绝对误差及平均绝对百分比误差均小于直接预测方法,证明了组合预测方法对滚动轴承振动信号具有更高的预测精确度。
4 现场应用
山西省晋城市某选煤厂通过主井带式输送机监测系统对电动机、减速器等关键设备的滚动轴承振动信号进行监测。该系统将振动信号幅值作为判断设备是否正常运行的主要指标之一。文献[15]指出振动信号符号化序列的标准差能够反映设备的运行状况。为了实现轴承运行状况预测,直接对轴承振动信号符号化序列标准差进行预测。系统每3 h采集1次轴承振动信号,每次采集8 000个点,并保存在数据文件中。对已采集的81个数据文件分别计算符号化序列标准差,如图11所示,并将其作为训练样本对SVM预测模型进行训练,对82—85 4个数据文件符号化序列标准差进行预测。
表1 组合预测方法和直接预测方法误差对比
Table 1 Error comparison between combined prediction method and direct prediction method
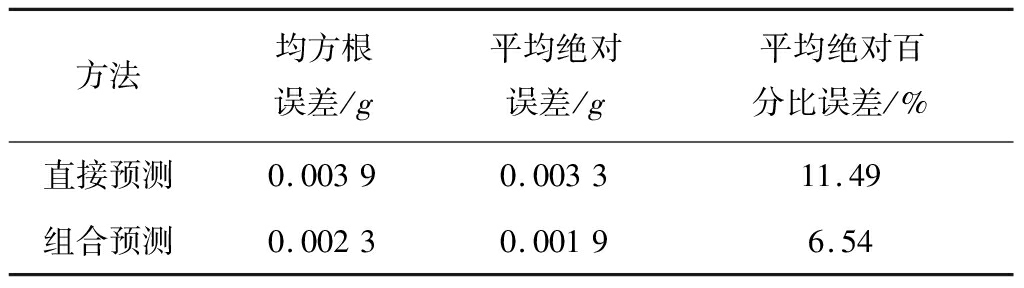
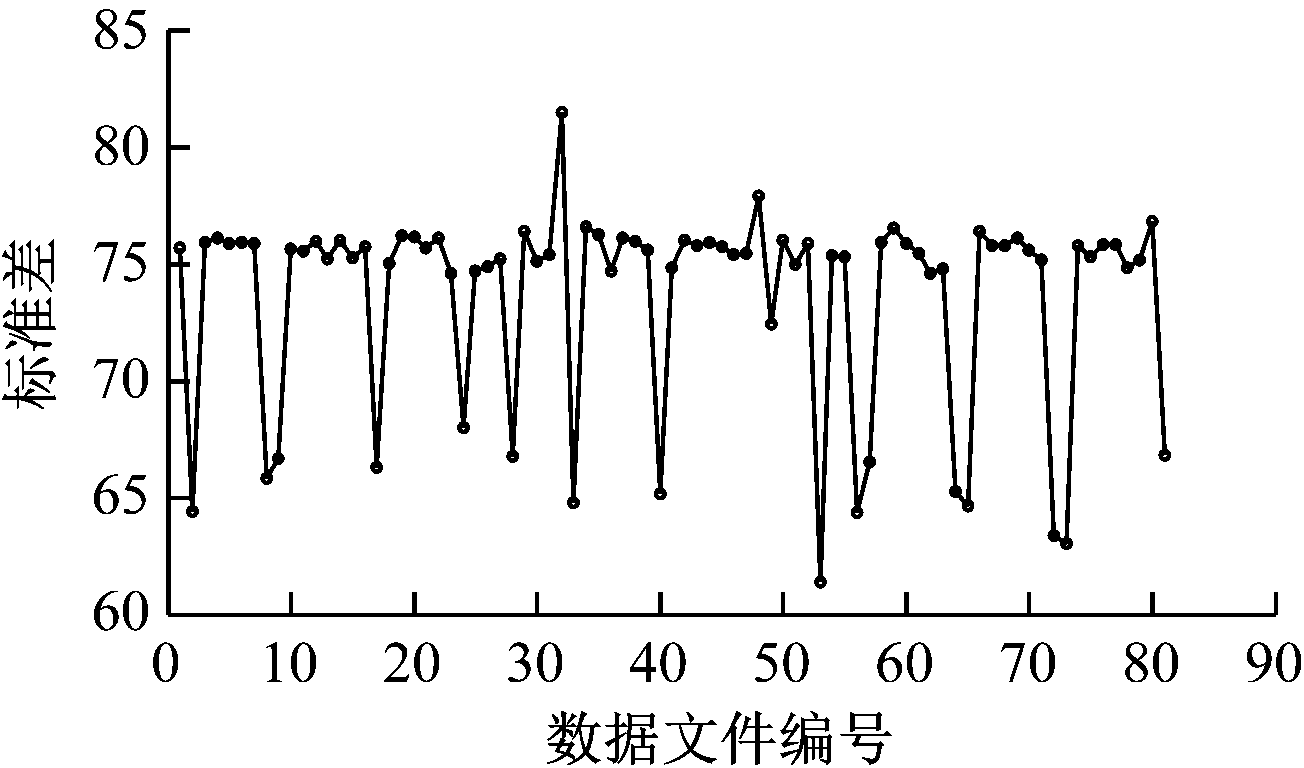
图11 81个数据文件符号化序列标准差
Fig.11 Symbolized sequence standard deviation of 81 data files
采用组合预测方法将高频子序列各采样点信号构造为二维特征对SVM预测模型进行训练,得到高频子序列的4个预测值。将低频子序列及趋势项对应的各采样点信号构造为四维特征对SVM预测模型进行训练,得到低频子序列的4个预测值。然后将高低频子序列预测值进行叠加,得到原始信号的预测值,如图12所示,预测误差见表2。可看出预测的4个符号化序列标准差最大值为80.56,最小值为67.94,预测值在正常范围内,没有突变的异常趋势,显示设备在预测时间段内会平稳运行。设备实际运行平稳,未出现故障,与预测结果一致。

图12 振动信号符号化序列标准差预测值
Fig.12 Standard deviation prediction values of signifying sequence of vibration signals
表2 预测误差
Table 2 Prediction errors

5 结论
(1)提出了一种煤矿机械振动信号组合预测方法。该方法将原始振动信号划分为高频子序列和低频子序列,并分别进行预测,再对二者的预测结果进行叠加,得到最终预测结果。采用轴承实验数据对组合预测方法的有效性进行了验证,结果表明组合预测方法的均方根误差、平均绝对误差和平均绝对百分比误差均小于直接预测方法。该组合预测方法应用于某选煤厂设备滚动轴承运行状况预测,预测结果与实际情况相符。
(2)根据经验和试验对高低频分量进行划分,缺少数学模型,需要在后续工作中进行深入研究。
参考文献(References):
[1] 程晓涵,汪爱明,苏一新,等.投影寻踪方法在设备预知维护中的应用研究[J].振动工程学报,2016,29(4):631-637.
CHENG Xiaohan,WANG Aiming,SU Yixin,et al.Study on application of projection pursuit method in predictive maintenance for equipments[J].Journal of Vibration Engineering,2016,29(4):631-637.
[2] 张鑫媛.基于数据驱动的采煤机摇臂传动系统故障诊断方法研究[D].西安:西安科技大学,2019.
ZHANG Xinyuan.Research on fault diagnosis method of rocker drive system of shearer based on data drive[D].Xi'an:Xi'an University of Science and Technology,2019.
[3] 李赟恒.基于BP神经网络的采煤机截割部故障诊断研究[D].西安:西安科技大学,2017.
LI Yunheng.Research on fault diagnosis technology of shearer cutting unit based on BP nerual network[D].Xi'an:Xi'an University of Science and Technology,2017.
[4] 关长江.采煤机摇臂故障诊断问题研究[D].阜新:辽宁工程技术大学,2017.
GUAN Changjiang.Research problem for the shearer of ranging arm fault diagnosis[D].Fuxin:Liaoning Technical University,2017.
[5] 华伟.基于多小波变换的矿用齿轮箱故障诊断研究[D].北京:中国矿业大学(北京),2017.
HUA Wei.Fault diagnosis research of mine gearbox based on multiwavelets transform[D].Beijing:China University of Mining and Technology(Beijing),2017.
[6] 董绍江.基于优化支持向量机的空间滚动轴承寿命预测方法研究[D].重庆:重庆大学,2012.
DONG ShaoJiang.Research on space bearing life prediction method based on optimized support vector machine[D].Chongqing:Chongqing University,2012.
[7] 薛小兰,温秀兰,张鹏.基于遗传神经网络的机械振动信号预测[J].弹箭与制导学报,2007,27(3):239-240.
XUE Xiaolan,WEN Xiulan,ZHANG Peng.Pridiction of mechanical vibration signals based on genetic algorithms and neural network[J].Journal of Projectiles,Rockets,Missiles and Guidance,2007,27(3):239-240.
[8] 杨俊燕,张优云,赵荣珍.支持向量机在机械设备振动信号趋势预测中的应用[J].西安交通大学学报,2005,39(9):950-953.
YANG Junyan,ZHANG Youyun,ZHAO Rongzhen.Application of support vector machines in trend prediction of vibration signal of mechanical equipment[J].Journal of Xi'an Jiaotong University,2005,39(9):950-953.
[9] 吕建新,吴虎胜,王茂生,等.基于EMD和SVM的农用柴油机故障诊断研究[J].安徽农业科学, 2010,38(17):9225-9228.
LYU Jianxin,WU Husheng,WANG Maosheng,et al.Fault dignosis for agricultural diesel engine based on EMD and SVM[J].Journal of Anhui Agricultural Science,2010,38(17):9225-9228.
[10] AN Xueli, JIANG Dongxiang,ZHAO Minghao,et al.Short-term prediction of wind power using EMD and chaotic theory[J].Communications in Nonlinear Science & Numerical Simulation,2012, 17(2):1036-1042.
[11] HUANG Shengzhi,CHANG Jianxia,HUANG Qiang,et al.Monthly streamflow prediction using modified EMD-based support vector machine[J].Journal of Hydrology,2014,511(7):764-775.
[12] 李彩虹.两类组合预测方法的研究及应用[D].兰州:兰州大学,2012.
LI Caihong.Two types of combination forecasting methods and their applications[D].Lanzhou:Lanzhou University,2012.
[13] 朱霄珣.基于支持向量机的旋转机械故障诊断与预测方法研究[D].保定:华北电力大学,2013.
ZHU Xiaoxun.Research on rotating machine fault diagnosis and preditcion method based on support vector machine[D].Baoding:North China Electric Power University,2013.
[14] 林超.结合异常检测算法的轴承故障检测研究[D].杭州:浙江大学,2017.
LIN Chao.Research on bearing fault detection based on anomaly detection algorithm[D].Hangzhou:Zhejiang University,2017.
[15] 胡世杰.基于符号化时间序列分析的轴承故障诊断方法研究[D].南京:东南大学,2015.
HU Shijie.Symbolic time series analysis-based rolling bearing fault diagnosis[D].Nanjing:Southeast University,2015.