收稿日期:2019-12-17;修回日期:2020-09-25;责任编辑:胡娴。
基金项目:国家自然科学基金项目(51475249);山东省重点研发计划项目(2018GGX103016);山东省高等学校科技计划项目(J15LB10)。
作者简介:窦连城(1996-),男,山东潍坊人,硕士研究生,研究方向为机械故障诊断与无损检测,E-mail:jun368542624364@163.com。
引用格式:窦连城,战卫侠.钢丝绳断丝损伤漏磁场计算与仿真研究[J].工矿自动化,2020,46(10):87-91.
DOU Liancheng,ZHAN Weixia.Calculation and simulation research on leakage magnetic field of broken wire damage of wire rope[J].Industry and Mine Automation,2020,46(10):87-91.
0 引言
钢丝绳具有强度高、柔韧性好、质量小、工作平稳且不易骤然拉断的特性,常用于物料搬运、矿井提升及其他牵引和承载工作中。因为钢丝绳应用广泛且工作环境恶劣,极易产生损伤,所以钢丝绳损伤检测至关重要[1-3]。钢丝绳最常见的损伤形式之一是断丝损伤。钢丝绳缺陷的最终表现形式为断丝,而断丝又是钢丝绳断裂的前期征兆,因此,国内外权威检测机构均以钢丝绳断丝情况作为钢丝绳报废标准的主要指标[4]。漏磁检测是钢丝绳无损检测最常用的方法之一[5]。但是,基于漏磁法采集的信号中含有较多噪声,如股波噪声、外界电磁信号、振动干扰等,影响损伤信号分析的准确性。对漏磁场进行理论计算,获得其数值模型,可以得到缺陷处漏磁场的无噪声信号,有助于漏磁信号分析及损伤信号分类。
漏磁场的理论计算方法主要包括解析法和数值法[6]。其中解析法采用的是磁荷模型,即磁偶极子。磁偶极子是类比电偶极子而建立的物理模型。具有等值异号的2个点磁荷构成的系统称为磁偶极子,2个点磁荷释放的磁场类似于缺陷的漏磁场。1966年N. N. Zatsepin和V. E. Shcherbin最早对缺陷漏磁场进行定量分析,开始将磁偶极子模型应用到缺陷漏磁场分析中。此后,对缺陷漏磁场的理论分析不断深入。D. A. G. Trevino等[7]提出一种改进的三维漏磁偶极子模型,采用2个参数描述法向漏磁分量,用于分析圆锥、球形等缺陷形状;S. M. Dutta等[8]采用磁偶极子理论,以表面积分的形式得到缺陷的三维漏磁场;李忠吉等[9]根据材料力磁关系和磁荷理论,提出考虑磁荷实际分布的缺陷自漏磁场计算方法,并将该方法应用到某埋地管道磁记忆检测中;时朋朋[10]将磁荷理论应用到不同断口形状的缺陷漏磁场中,并获得漏磁场解析表达式。此外,文献[11-14]也分别将磁荷模型应用到铁磁材料的缺陷漏磁计算中。
钢丝绳结构复杂,缺陷状态及特征具有随机性,针对不同形态损伤进行物理计算难度太大,只能支持简化模型的计算,且对于不同形式的损伤状态,用同一种物理模型得到的结果不尽相同。随着有限元仿真方法的普及,使得对任意形状和位置的损伤研究成为可能。采用有限元离散形式,通过大矩阵快速压缩算法可将电磁场计算难题转换为一系列矩阵求解问题。通过有限元方法得到的仿真模型计算较精细,可用于验证通过理论计算得到的磁荷模型。因此,本文采用磁荷模型对钢丝绳缺陷漏磁场进行理论分析,并采用有限元仿真进行验证。
1 基于磁荷理论的钢丝绳断丝漏磁场分析
漏磁检测技术被广泛应用于连续铁磁结构的局部损伤诊断中,具有快速、非接触的优点[15-17]。在损伤检测过程中,磁化的铁磁材料可视为磁铁,其产生的磁场遇到由缺陷产生的小气隙时,磁场就会扩散开。因为单位体积的空气不能像磁铁那样承载过多的磁场,所以当磁场扩散时,它开始从铁磁材料中泄漏出来,产生漏磁场[18]。用磁敏元件检测漏磁场,对检测信号进行分析处理,可得到损伤信息,这是漏磁检测的基本原理。
漏磁场的分析计算模型包括二维磁荷模型、三维磁荷模型及改进模型,由于二维磁荷模型计算相对简单且通用性较强,本文采用二维磁荷模型对钢丝绳缺陷漏磁场进行分析计算。假设钢丝绳2处断面所产生的漏磁场由2个磁荷量相等的点磁荷Q1(正磁荷)和Q2(负磁荷)产生,钢丝绳直径为d,断口间距为2δ,2个点磁荷距离为2l,漏磁场二维磁荷模型如图1所示。其中,r1和r2分别为由Q1,Q2指向P点的向量。钢丝绳沿轴向磁化,当遇到损伤时,大部分磁力线被转移到缺陷周围,在缺陷断面上产生相反的磁荷或磁偶极子。因为单根钢丝绳断口所产生的漏磁场是轴对称场,所以只需计算断口在钢丝绳轴线平面内的磁场分布[19]。
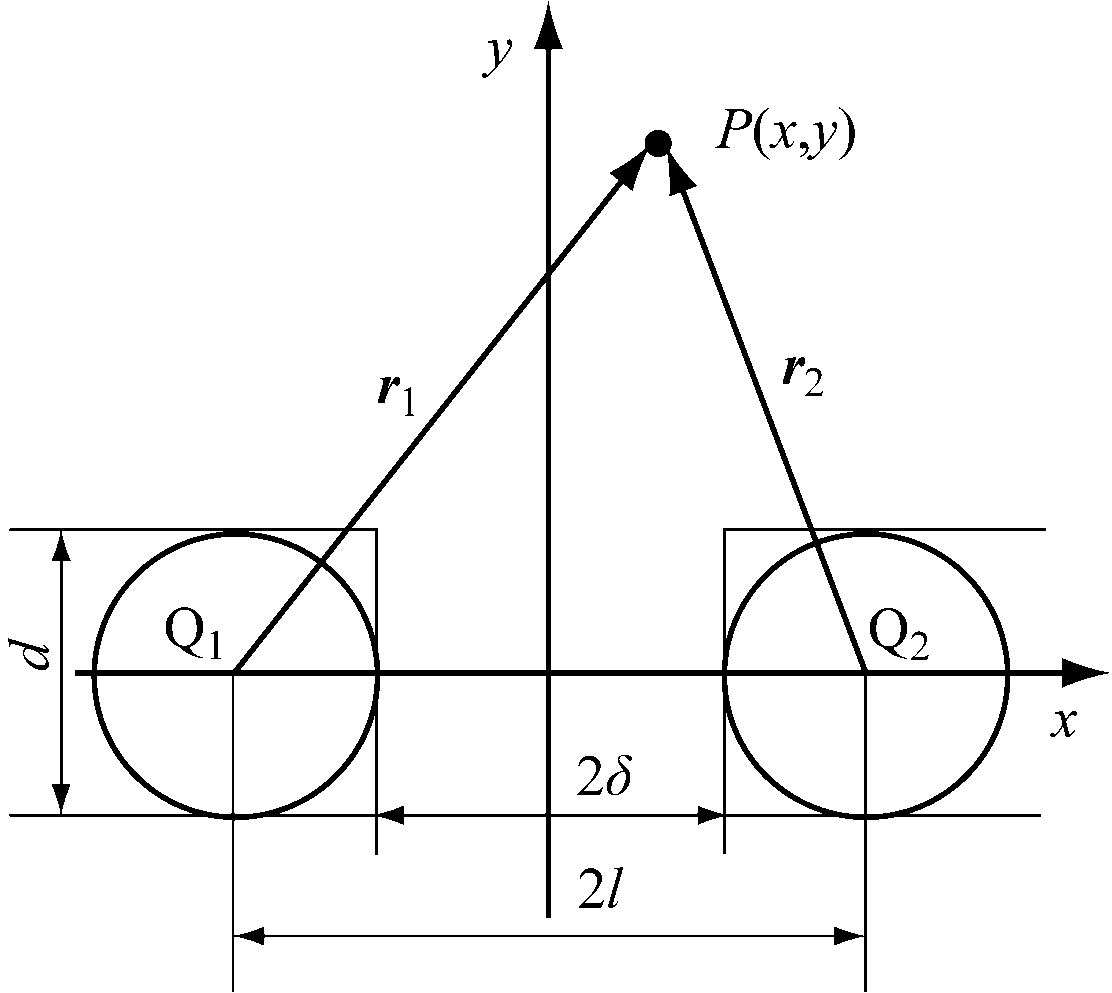
图1 漏磁场磁荷模型
Fig.1 Magnetic charge model of leakage magnetic field
由磁荷理论和磁场叠加原理可知,2个点磁荷在任一点P(x,y)处所产生的磁感应强度B等于点磁荷Q1和Q2在P点产生的磁感应强度的向量和。根据磁荷模型,点磁荷Q1在P点产生的磁场强度为
(1)
式中:μ0为真空磁导率;qm为磁偶极子中点磁荷Q1的磁荷量。
真空磁导率定义为磁感应强度B与磁场强度H的比值,因此有
B=μ0H
(2)
点磁荷Q1在P点产生的磁感应强度在x轴、y轴方向的分量分别为
(3)
(4)
式中θ为点磁荷Q1与P点的连线和x轴之间的夹角。
图1中点磁荷Q1和Q2在P点产生的磁感应强度在x轴方向的分量和Bx、y轴方向的分量和By分别为
Bx=Bx1+Bx2=
(5)
By=By1+By2=
(6)
式中:Bx2为Q2在P点产生的磁感应强度在x轴方向的分量;By2为Q2在P点产生的磁感应强度在y轴方向的分量。
要计算磁感应强度B,需要确定l与磁荷qm的值,其中l为变化量,对于单根丝漏磁模型,qm计算公式为
qm=πλBmd2/4
(7)
式中:λ为折合系数,对于外层断丝,λ取1;Bm为断面处的漏磁强度,取0.37 T。
Bm计算公式为
Bm=(φ-φ′)/s
(8)
式中:φ为有缺陷股钢丝绳非缺陷位置断面的磁通量;φ′为有缺陷股钢丝绳缺陷位置断面的磁通量;s为缺陷断面的面积。
2 钢丝绳漏磁场有限元仿真
2.1 钢丝绳及励磁装置模型结构设计
因为钢丝绳结构的复杂性会导致计算量巨大,所以,以型号为6×37+IWS的钢丝绳为原型建立钢丝绳简化模型。钢丝绳几何参数如下:公称直径为24 mm,该公称直径下单根丝直径为1.1 mm,捻距为150 mm,长度为300 mm。在钢丝绳侧股中间的股峰位置做一处断丝损伤,同时建立永磁体励磁装置模型。永磁体励磁装置由永磁铁、衔铁、空气隙等组成,结构尺寸如下:衔铁外径为140 mm,内径为84 mm,长度为230 mm;磁铁外径为54 mm,内径为34 mm,轴向宽度为25 mm。通过Ansoft Maxwell软件建立励磁装置有限元模型,如图2所示。
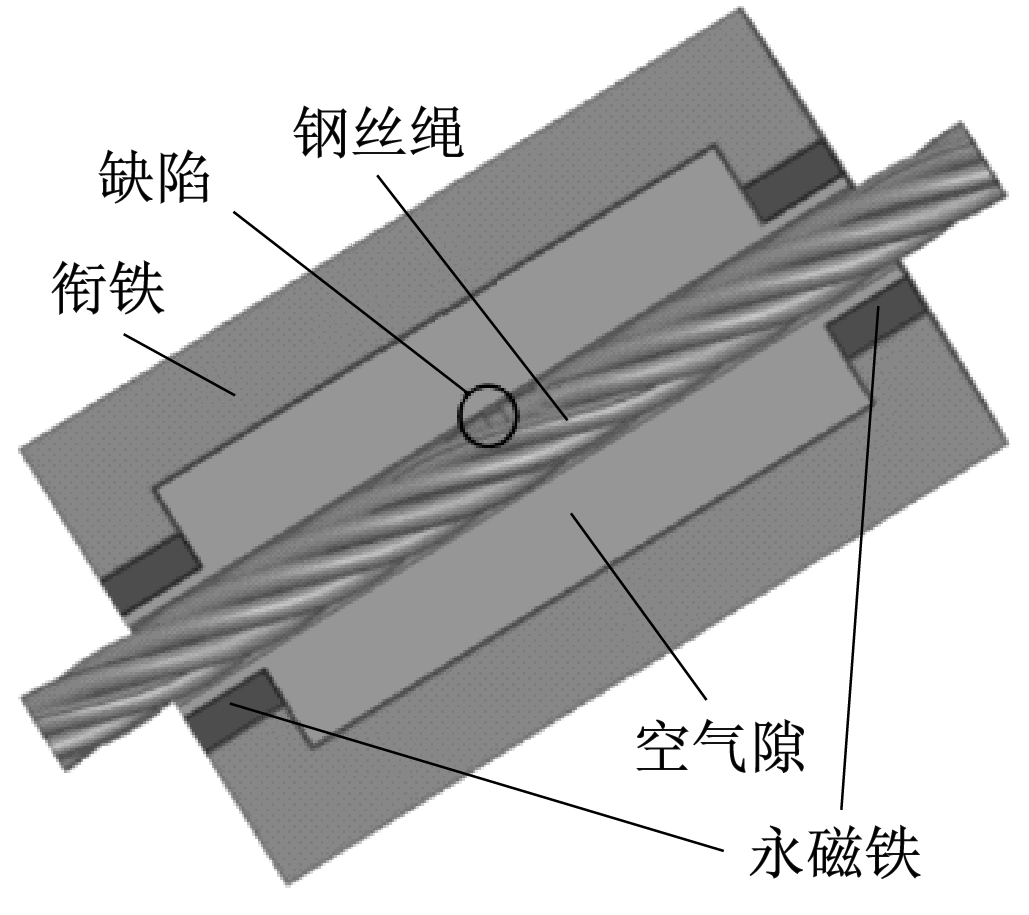
图2 励磁装置有限元模型
Fig.2 Finite element model of excitation device
电磁场的边值问题实际上是求解给定边界条件下的麦克斯韦方程组及由方程组演化出的其他偏微分方程问题。Ansoft Maxwell软件中三维静磁场求解器的基本麦克斯韦方程为

(9)
式中:J为电流密度;μ为介质磁导率。
2.2 钢丝绳及励磁模型材料选择
钢丝绳材料为优质碳素钢,其B-H曲线如图3所示。永磁铁材料为NdFe30,设置为径向充磁。衔铁材料为工业纯铁DT4,结构近似呈封闭型,起到屏蔽外磁场的作用。衔铁的B-H曲线如图4所示。
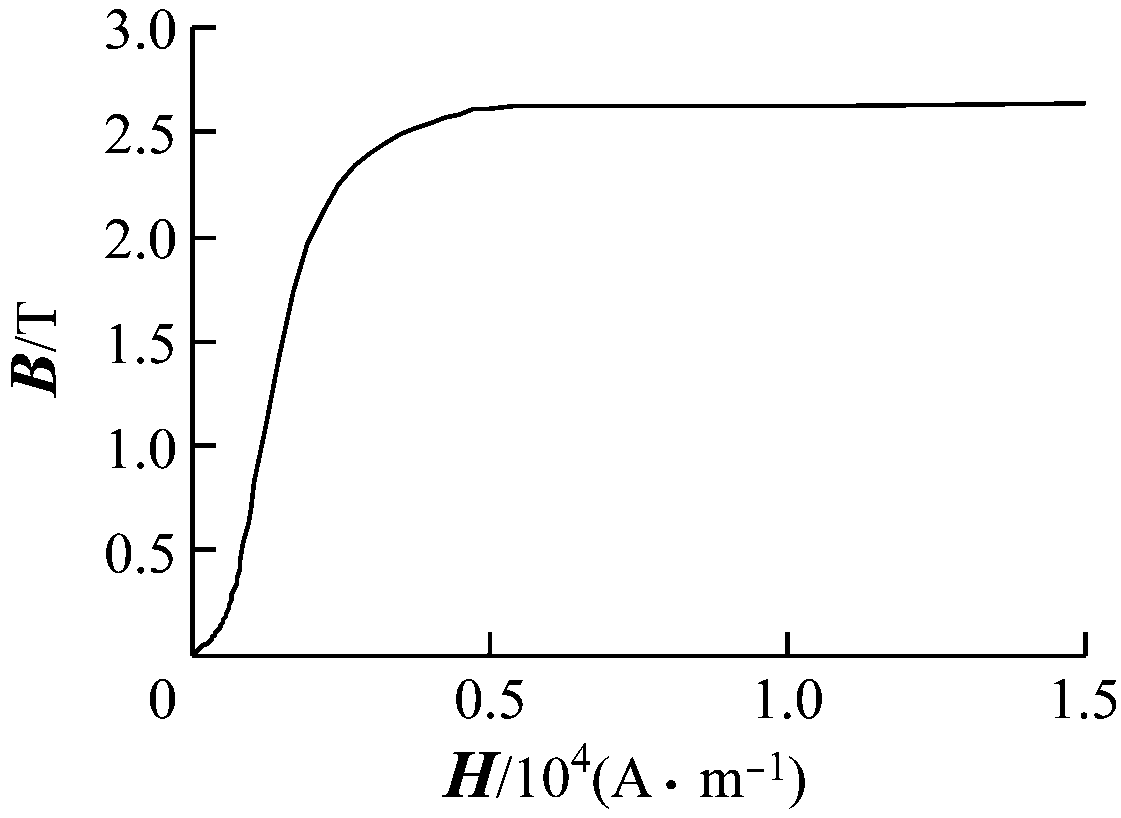
图3 钢丝绳的B-H曲线
Fig.3 B-H curve of wire rope

图4 衔铁的B-H曲线
Fig.4 B-H curve of armature
2.3 网格剖分及边界条件设定
网格划分是有限元仿真的重要步骤,对于非复杂结构,可采用软件的自适应方法进行网格划分,这样计算速度较快,结果也较准确。因此,本文中模型采用自适应网格进行剖分,如果网格存在缺陷,则进一步进行手动剖分。
求解区域为包括整个模型区域的真空区。边界条件为自然边界条件,这意味着跨越物体之间界面的磁场强度H的切向分量和磁感应强度B的法向分量是连续的且满足以下关系:
(10)
式中:Ht1,Ht2为分界面两侧磁场强度的切向分量;Bn1,Bn2为分界面两侧磁通密度的法向分量;Js为表面电流密度。
2.4 钢丝绳磁通密度云图
对于单根断丝模型,损伤处的漏磁场大小随单根断丝长度变化。因为轴向漏磁信号更容易被识别,所以本文仅研究钢丝绳断丝损伤轴向漏磁分量的变化趋势。
断口宽度为1 mm的单根断丝钢丝绳磁通密度云图及局部放大图如图5所示。从图5可看出,钢丝绳的饱和程度达到检测要求,钢丝绳损伤断面周围区域饱和程度明显降低。

(a) 磁通密度云图

(b) 损伤局部放大图
图5 单根断丝钢丝绳磁通密度云图及局部放大图
Fig.5 Cloud diagram of magnetic flux density and partial enlarged diagram of a single broken wire rope
3 结果分析
根据磁荷模型得到的轴向漏磁分量如图6所示,单根断丝的断口宽度取0.5~5 mm,间距为0.5 mm。通过有限元仿真模型得到的轴向漏磁分量如图7所示,由于仿真得到的信号较微弱,单根断丝的断口宽度取0.5,1,1.5,2,3,5 mm。
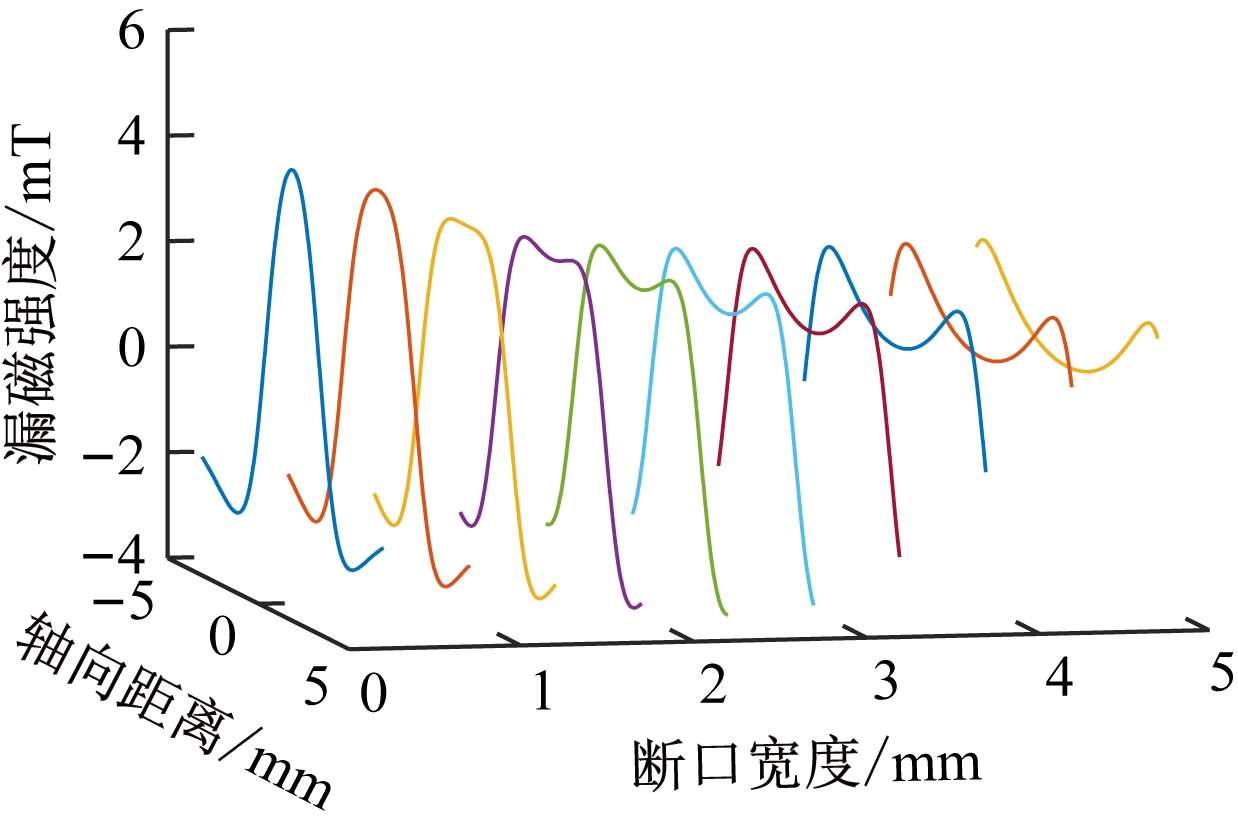
图6 通过磁荷模型得到的轴向漏磁分量
Fig.6 Axial magnetic flux leakage component obtained by magnetic charge model

图7 通过有限元仿真模型得到的轴向漏磁分量
Fig.7 Axial magnetic flux leakage component obtained by finite element simulation model
由图6可知,断口宽度较小时,漏磁信号只有1个峰值,随着断口宽度增加,漏磁强度峰值逐渐变小,变化幅度也较小;从第3条曲线开始,信号峰值陡峭度明显降低,断口宽度为1.5 mm左右时,曲线开始出现2个峰值,峰值间距等于断口宽度,断口宽度越大,峰值之间的凹陷越明显。
由图7可知,有限元仿真信号变化规律与磁荷理论分析结果基本一致,信号均在断口宽度逐渐增加的过程中出现了2个峰值,信号形状相似,仿真信号在断口宽度较小时,峰值变化幅度较大。
综合图6和图7可知:在缺陷断面处即磁荷位置,磁力线较密集,从此处发散的磁力线主要为径向漏磁;在向断口中心靠拢过程中,径向分量逐渐减小,轴向分量逐渐增加,同时磁力线也变得更加稀疏,两者相互作用,导致峰值出现后又产生峰值分化现象。此外,因为磁化钢丝绳近表面也有少量漏磁,所以磁荷模型的信号整体比仿真信号要小;近钢丝绳表面的少量漏磁会产生磁力线相斥现象,而磁荷模型忽略了该现象,使得其漏磁曲线中凹陷的产生要早于仿真模型。
4 结论
(1) 通过磁荷模型对钢丝绳单根断丝轴向漏磁场进行分析,得到漏磁场与断口宽度之间的关系,并通过有限元仿真验证理论分析结果的正确性。结果表明:用2种方法得出的漏磁强度变化大体一致,能反映单根断丝钢丝绳轴向漏磁分量的变化规律;在一定范围内,随着断口宽度增加,缺陷轴向漏磁强度呈现非线性减小的变化趋势,并且单一峰值逐渐分化为2个峰值。
(2) 由于钢丝绳结构复杂、损伤形式多样,本文仅进行了钢丝绳断丝损伤一般形式的简单计算,未考虑多根断丝、内部断丝等情况和断口形式的影响。同时,因为漏磁检测器不具有通用性,且信号降噪会产生失真现象,所以通过实验得到的漏磁曲线与本文中的曲线有一定差别。
参考文献(References):
[1] 谭继文,战卫侠,文妍.钢丝绳安全检测原理与技术[M].北京:科学出版社,2009.
TAN Jiwen,ZHAN Weixia,WEN Yan.The principle and technology of steel wire rope safety detection[M].Beijing:Science Press,2009.
[2] 战卫侠.钢丝绳断丝损伤信号处理及定量识别方法研究[D].青岛:青岛理工大学,2013.
ZHAN Weixia.Research on signal process and quantitative recognition method of broken wires in wire rope[D].Qingdao:Qingdao University of Technology,2013.
[3] 田劼,胡耀松,郭红飞,等.基于霍尔元件的矿用钢丝绳探伤仪研究[J].工矿自动化,2019,45(11):75-80.
TIAN Jie,HU Yaosong,GUO Hongfei,et al.Research on mine-used wire rope flaw detector based on hall element[J].Industry and Mine Automation,2019,45(11):75-80.
[4] 赵志科.矿井提升钢丝绳的动态检测与故障诊断方法研究[D].徐州:中国矿业大学,2018.
ZHAO Zhike.Study on dynamic detection and fault diagnosis approaches for mine hoisting wire rope[D].Xuzhou:China University of Mining and Technology,2018.
[5] SUN Yanhua,KANG Yihua.A new MFL principle and method based on near-zero background magnetic field[J].NDT & E International,2010,43(4):348-353.
[6] 施瀚.漏磁检测永磁铁磁回路的数学模型研究[D].沈阳:沈阳工业大学,2017.
SHI Han.Magnetic flux leakage detection mathematical model of permanent magnet ferromagnetic loops[D].Shenyang:Shenyang University of Technology,2017.
[7] TREVINO D A G,DUTTA S M,GHORBEL F H,et al.An improved dipole model of 3-D magnetic flux leakage[J].IEEE Transactions on Magnetics,2015,52(12):1-7.
[8] DUTTA S M,GHORBEL F H,STANLEY R K.Dipole modeling of magnetic flux leakage[J].IEEE Transactions on Magnetics,2009,45(4):1959-1965.
[9] 李忠吉,李长俊,成婷婷,等.埋地管道缺陷的自漏磁场计算方法研究[J].中国安全生产科学技术,2019,15(9):153-157.
LI Zhongji,LI Changjun,CHENG Tingting,et al.Study on calculation method of self-leakage magnetic field for defect of buried pipeline[J].Journal of Safety Science and Technology,2019,15(9):153-157.
[10] 时朋朋.缺陷漏磁场磁偶极子模型的若干解析解[J].无损检测,2015,37(3):1-7.
SHI Pengpeng.Analytical solutions of magnetic dipole model for defect leakage magnetic fields[J].Nondestructive Testing,2015,37(3):1-7.
[11] SURESH V,ABUDHAHIR A.An analytical model for prediction of magnetic flux leakage from surface defects in ferromagnetic tubes[J].Measurement Science Review,2016,16(1):8-13.
[12] LE M,LEE J,JUN J,et al.Estimation of sizes of cracks on pipes in nuclear power plants using dipole moment and finite element methods[J].NDT & E International,2013,58:56-63.
[13] SURESH V,ABUDHAIR A.Dipole model to predict the rectangular defect on ferromagnetic pipe[J].Journal of Magnetics,2016,21(3):437-441.
[14] 黄作英,阙沛文.应用磁荷法建立漏磁信号模型[J].应用基础与工程科学学报,2006,14(1):115-120.
HUANG Zuoying,QUE Peiwen.Application of dipole magnetic charge method to MFL signal analytical model[J].Journal of Basic Science and Engineering,2006,14(1):115-120.
[15] PARK S,KIM J W,LEE C,et al.Magnetic flux leakage sensing-based steel cable NDE technique[J/OL].Shock and Vibration:1-8[2019-11-20].https://doi.org/10.1155/2014/929341.
[16] SHI Yan,ZHANG Chao,LI Rui,et al.Theory and application of magnetic flux leakage pipeline detection[J].Sensors,2015,15(12):31036-31055.
[17] KIM J W,PARK S.Magnetic flux leakage sensing and artificial neural network pattern recognition-based automated damage detection and quantification for wire rope non-destructive evaluation[J].Sensors,2018,18(1):109.
[18] KIM J W,PARK S.Magnetic flux leakage-based local damage detection and quantification for steel wire rope non-destructive evaluation[J].Journal of Intelligent Material Systems and Structures,2018,29(17):3396-3410.
[19] MANDACHE C,CLAPHAM L.A model for magnetic flux leakage signal predictions[J].Journal of Physics D:Applied Physics,2003,36(20):2427.