0 引言
目前,中国大部分煤矿企业采用钻孔方式抽采瓦斯,由于钻头在煤层中的路径难以获取,一般通过计算钻杆数量来间接计算钻孔深度,以满足钻孔深度设计要求[1-3]。传统的钻杆数量人工统计方式存在自动化程度低、受人为因素影响、误差较大等缺点[4-5]。有学者采用传感器、声波等检测钻杆数量或钻孔深度,如仇海生等[6]基于声波回声技术测量钻孔深度,但存在测量设备体积较大、检测距离有限等问题。路拓等[7]基于弹性波理论,在钻杆底端激发、接收弹性波,实现瓦斯抽采钻孔快速抽查,但由于钻孔存在角度偏差,探测精度较低。董立红等[8]提出一种基于改进Camshift算法的钻杆计数方法,通过Camshift算法追踪钻杆特征目标,根据追踪路径统计钻杆数量,但该方法对环境光线变化过于敏感,易造成统计结果偏差。
针对上述问题,本文提出一种基于改进ResNet网络的井下钻杆计数方法。通过ResNet网络判断视频中每一帧图像是否包含卸杆动作,并基于Logistic经验曲线自动更新学习率,以提高模型分类准确率;通过积分法对视频分类置信度进行滤波,最后统计置信度曲线下降沿数量,实现钻杆计数。
1 井下钻杆计数方法原理
基于改进ResNet网络的井下钻杆计数方法流程如图1所示,包括数据集建立和预处理、图像分类模型选取和训练、钻杆数量统计3个部分[9]。
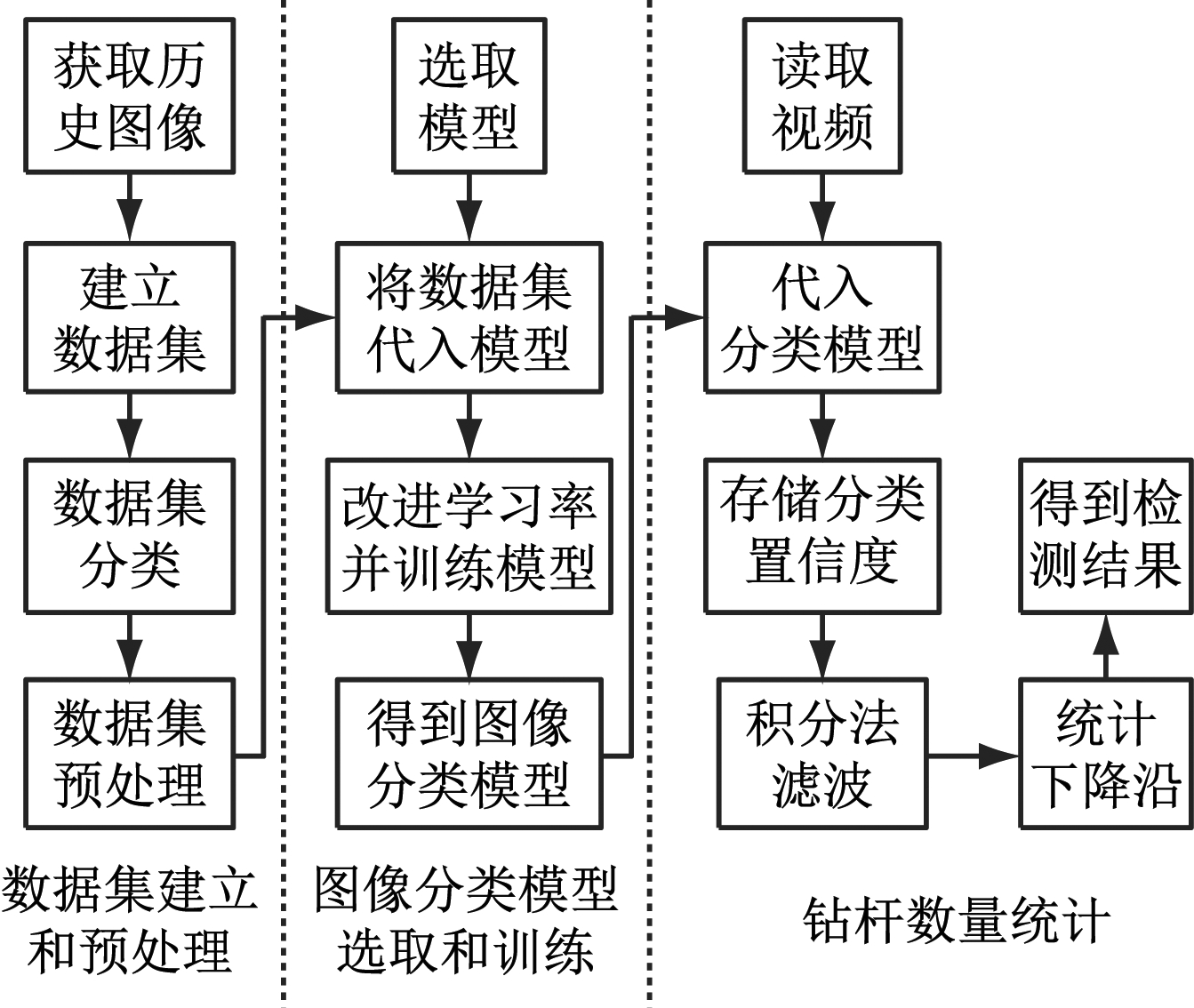
图1 基于改进ResNet网络的井下钻杆计数方法流程
Fig.1 Process of underground drill pipe counting method based on improved ResNet network
数据集建立和预处理过程:① 获取历史图像并建立数据集;② 按照图像特征,将收集的数据手动分为正在卸杆与非卸杆2类;③ 数据集预处理,对数据集进行扩充。
图像分类模型选取和训练过程:① 选取合适的图像分类模型;② 将数据集代入分类模型;③ 对分类模型进行改进和训练,优化模型输出结果。
钻杆数量统计过程:① 将卸杆视频代入分类模型;② 存储模型输出的每帧图像的分类结果与置信度;③ 用积分法对视频分类置信度进行滤波;④ 统计并输出钻杆计数结果。
2 井下钻杆计数方法实现
2.1 图像分类模型构建
与Camshift目标跟踪算法相比,深度学习算法能够有效、自动提取图像特征,简化操作流程[10]。当深度学习模型在10层以下时,易出现梯度消失、梯度爆炸现象[11-12];当模型增至10层以上时,由于模型深度加大,在训练中易出现退化现象,导致准确率下降[13]。K. He等[14]提出的残差网络(Residual Network,ResNet)通过残差块与batchnorm归一化,有效解决了梯度爆炸、模型退化问题,因此,本文选用ResNet构建图像分类模型。为提取图像中卸杆时的有效信息,需要相对较深的网络结构。为保证模型最终的测试精度、减少训练时间,本文使用ResNet-50模型对图像进行分类训练。
ResNet-50结构如图2所示。通过5段卷积层与全连接层对输入图像进行处理后,再通过分类器判断数据的置信度,以此判断图像类别。使用ReLU作为激活函数,与sigmoid,tanh等其他激活函数相比,ReLU收敛速度更快。

图2 ResNet-50结构
Fig.2 ResNet-50 structure
以ResNe-50三层残差块为例,其一般形式如图3所示。其中,X为残差块输入,经过三层卷积运算后,输出Y:
Y=F(X,W1,W2,W3)+WX
(1)
式中:W1,W2,W3为每层的学习权重;W为将输入X转换为输出的权值。

图3 三层残差块的一般形式
Fig.3 General form of three-layer residual block
2.2 学习率更新策略
模型训练期间,权重更新的量称为步长或学习率。学习率是最影响模型训练结果的超参数之一,良好的学习率更新策略能够保证模型更快达到损失的最小值,提高模型分类准确率,还能保证模型不陷入局部最优解,对模型训练结果的导向有重要意义。
学习率设置标准:在训练开始阶段,选用较大的学习率,防止模型陷入局部最优,加快模型收敛速度;随着训练批次增加,学习率逐渐减小,更接近模型最优解。一般而言,可以利用过去的经验(或其他类型的学习资料)直观地设定学习率的最佳值。当已经设定好学习率并训练模型时,只有等学习率随着时间的推移而下降,模型才能最终收敛。然而,随着梯度达到高原,训练损失更难得到改善。针对上述问题,本文结合线性学习率预热和基于Logistic曲线的学习率衰减策略进行学习率更新,以提高模型准确率。
模型中所有参数的初始值都是随机值,而初始学习率过高可能会导致模型不稳定。因此,需进行学习率预热,即在开始阶段设置较小的学习率,随着训练批次增加,逐步提高学习率。提取训练中前10%的批次进行线性学习率预热,使学习率从0开始线性增长至初始学习率η1。预热阶段的学习率更新公式为
η=η1i/m
(2)
式中:η为第i(1≤i≤m)批次的学习率;m为总学习批次的10%。
在迭代优化的后期,逐步减小学习率的值,有助于算法收敛,更容易接近最优解。因此,需采用一定的学习率衰减策略。目前常用的学习率衰减方法是分段常数衰减,但该方法分段间隔大、更新速度慢[15]。针对该问题,本文提出利用Logistic曲线更新学习率。Logistic曲线公式为
(3)
式中:y为输出;K,a,b为未知参数;x为输入。
学习率太大可能会导致模型出现振荡现象,因此,本文设学习率不超过1,令K=1。当a<0,b>0时,Logistic曲线为下降曲线,下降曲线的特点是开始缓慢下降,中间迅速下降,达到某一限度后缓慢下降。
衰减阶段的学习率更新公式为
(4)
式中:η′为第m′批次的学习率;m < m′≤ n′, n′为总学习批次。
结合学习率预热与衰减2种更新策略,将总学习批次的前10%设置为学习率预热部分,后90%设置为Logistic衰减部分,得到综合学习率曲线,如图4所示。

图4 学习率变化曲线
Fig.4 Curve of learning rate
2.3 置信度数据滤波
完成模型训练后,将待检测视频输入模型,得到视频中每帧图像的分类置信度,并按照时间顺序存储至CSV(Comma-Separated Values)文件中。由于模型检测存在一定误差,难以直接通过分类置信度计算钻杆数量。为便于统计钻杆数量,降低模型检测误差,选用积分法对分类置信度数据进行滤波,将其转换为0,1信号。设CSV文件中存储的置信度数据为f(x),连续5个数据点进行一次积分,积分公式为
(5)
式中:n为正整数,5(n+1)≤输入视频总帧数;φ为积分参考值,0.5≤φ≤0.8。
若式(5)的计算结果大于0,则该段5帧图像为卸杆过程图像,将该5帧连续数据记录为1;若式(5)的计算结果小于0,则该段5帧图像为非卸杆过程图像,将该5帧连续数据记录为0。
为加快检测速率,对积分过程进行简化,以减少滤波计算量。在实际生产中,可采用下式进行滤波:
(6)
通过式(6)将输入视频或图像的分类置信度全部转换为0或1,最后计算置信度波形下降沿数量,即为该段视频中包含的卸杆数量。
3 实验分析
3.1 数据集制作
提取原始采集图像中有代表性的1 500张图像作为钻杆分类的原始数据集,并统一转换为224×224的图像。其中,工人正在卸杆的图像作为分类数据集的第1类,样本数量为670;其余时刻图像作为分类数据集的第2类,样本数量为830。
为了提高训练模型的准确率,需增加数据集样本数量,采用图像翻转、图像旋转与亮度增强操作对样本进行预处理。以第1类图像为例,预处理后的图像如图5所示。

(a) 卸杆样本图像

(b)
图像旋转样本

(c)
图像翻转样本

(d)
图像亮度增强样本
图5 图像预处理结果
Fig.5 Image preprocessing results
3.2 学习率更新策略验证
3.2.1 学习率衰减经验公式
由式(4)可得,参数b的变化关系到曲线中间缓冲区陡峭或平滑,参数a的变化关系到曲线的左移或右移。若b值相对较大,会导致曲线陡峭,与分段学习率衰减曲线相似;若b值相对较小,则输出结果变化相对较小。为此,在无衰减学习率为0.002、总学习批次n′为100的情况下,以衰减曲线过学习批次中点为前提(即输出为0.5、输入为n′/2时,a=-50b),先对参数b取值,讨论曲线梯度对模型输出的影响。共进行50组测试,选取其中有代表性的3组进行分析,并与无衰减和分段衰减情况比较,见表1。
表1 参数b对模型分类结果的影响
Table 1 Influence of parameter b on model classification results
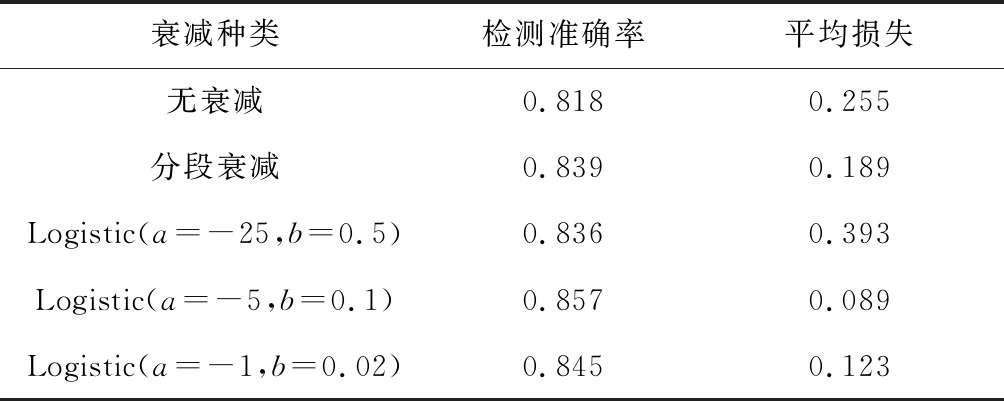
衰减种类检测准确率平均损失无衰减0.8180.255分段衰减0.8390.189Logistic(a=-25,b=0.5)0.8360.393Logistic(a=-5,b=0.1)0.8570.089Logistic(a=-1,b=0.02)0.8450.123
由表1可知,当b=0.1时,即b=10/n′的情况下,模型准确率相比无衰减情况提升3.9%,并且能够有效降低模型损失。若a值相对较大,会导致曲线左移,处于低学习率批次增多,反之,会导致高学习率批次增多。为此,本文先选定参数b=10/n′,对参数a的取值进行探讨。共进行20组测试,选取其中有代表性的5组结果进行分析,见表2。
表2 参数a对模型分类结果的影响
Table 2 Influence of parameter a on model classification results
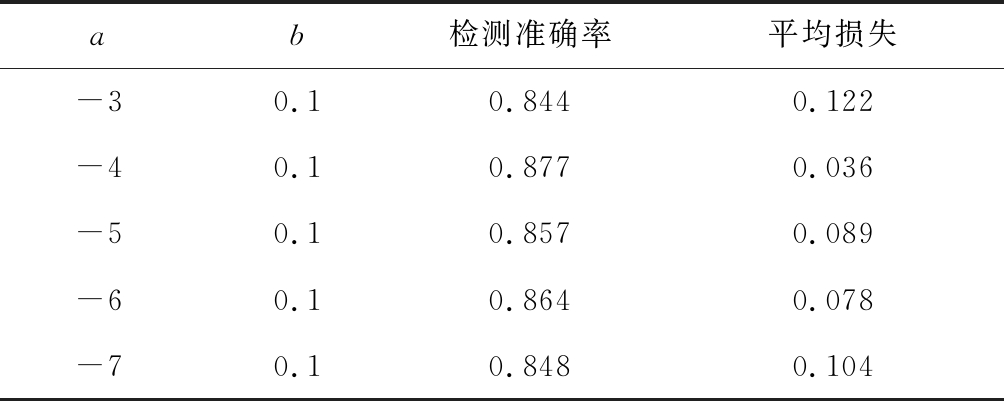
ab检测准确率平均损失-30.10.8440.122-40.10.8770.036-50.10.8570.089-60.10.8640.078-70.10.8480.104
由表2可知,在b值固定的基础上,当a=-6~-4时,即(-n′b/2)-1<a<(-n′b/2)+1,-2a≈n′b的情况下,分类模型能够取得较优的分类结果。
经过多次实验并比较a,b取值对模型分类结果的影响,发现分类模型能够取得较优的分类结果时,b值主要集中在5/n′~20/n′内。基于上述实验结果,结合式(4),可得出预热阶段的学习率更新经验公式:

(7)
3.2.2 模型分类结果
采用衰减+预热2种策略训练模型后,模型训练的准确率与损失如图6所示。从图6可看出,模型经过训练后,最终损失下降至0.1以内,训练准确率达到0.98以上,说明该模型具有较高的准确率。

(a) 训练模型准确率曲线
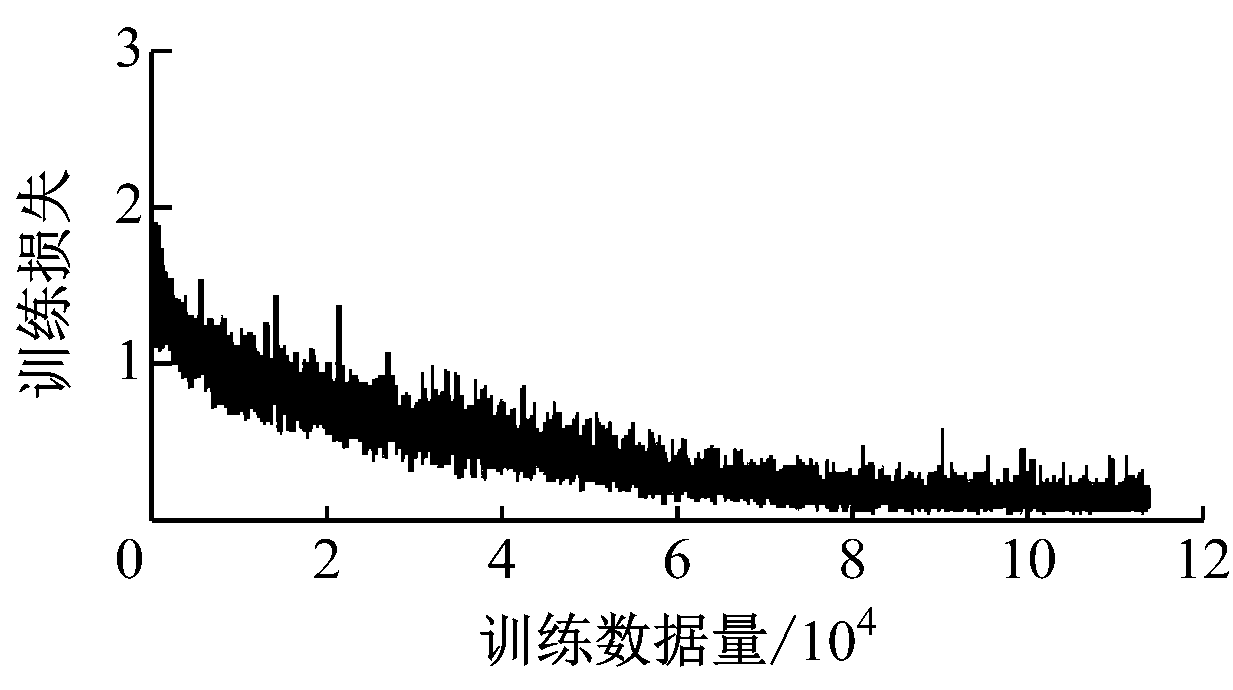
(b) 训练模型损失曲线
图6 训练模型准确率及损失曲线
Fig.6 Accuracy and loss curves of training model
在完成模型训练后,通过1 900组卸杆实验对3种学习率更新策略的效果进行对比,结果见表3。由表3可知,预热+衰减的更新策略效果最好,分类检测准确率为0.890,即89%。
表3 学习率更新策略效果对比
Table 3 Comparison of effect of learning rate updating strategy

学习率更新策略检测准确率平均损失无预热、无衰减0.8180.255预热0.8640.313预热+衰减0.8900.029
3.3 钻杆计数结果
将训练完成的模型保存至本地,模型接收普通视频与单帧图像输入。人工卸杆平均耗时4~5 s/根,为加快模型检测速度,同时,不影响卸杆过程的完整性,将视频的帧率由24帧/s降至2帧/s。
将卸杆视频输入分类模型后,得出图像置信度并以百分比形式在图像上标注,然后通过积分法进行滤波,得出分类结果。图像分类过程如图7所示。

(a) 卸杆时刻图像

(b) 非卸杆时刻图像
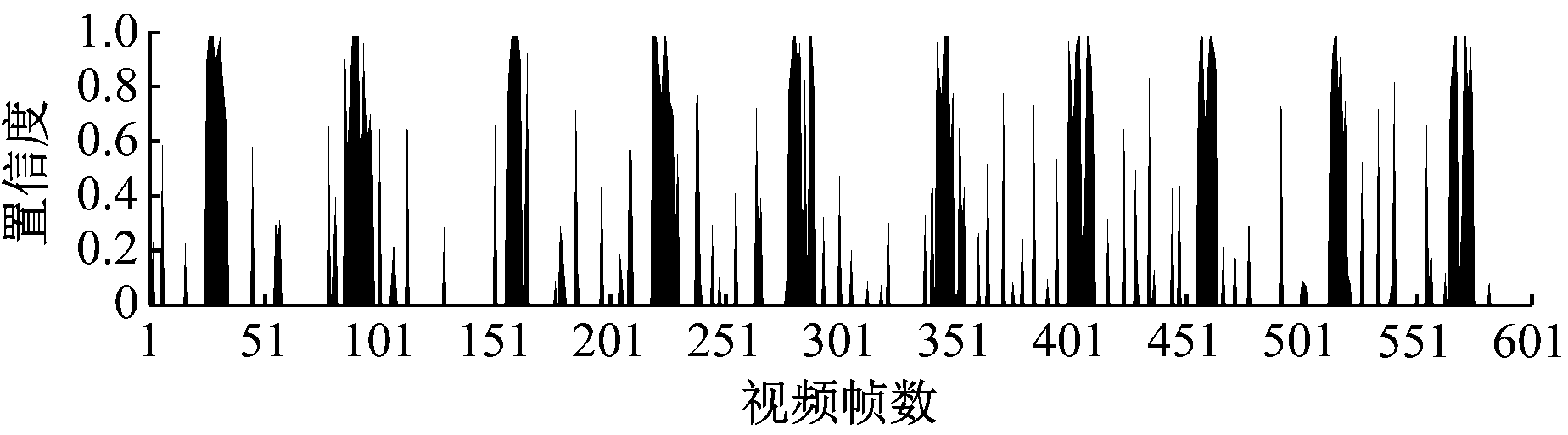
(c) 卸杆置信度
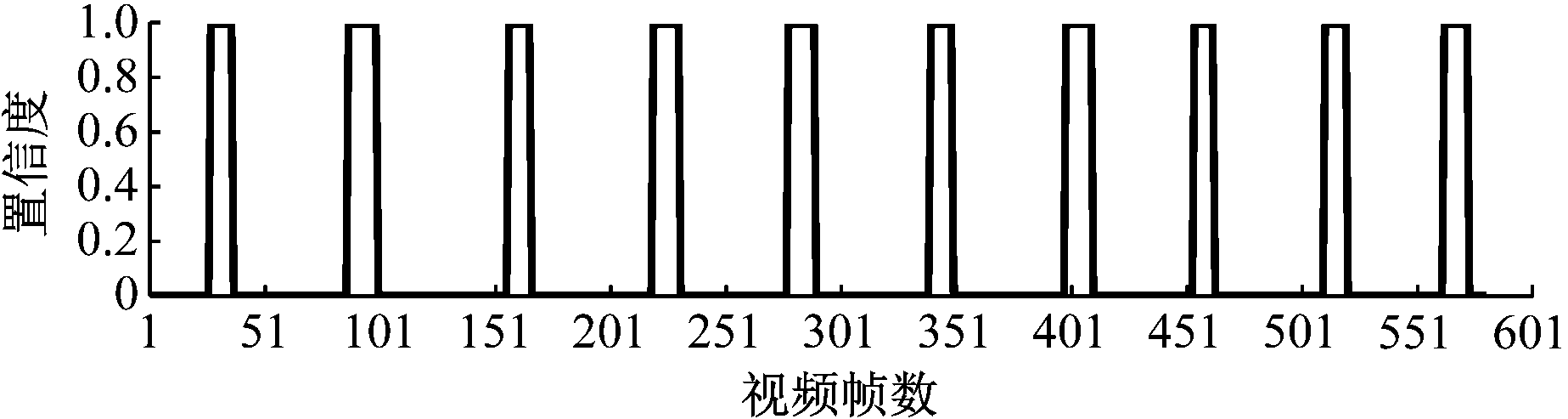
(d) 积分法滤波结果
图7 图像可视化分类过程
Fig.7 Image visualization classification process
选取打钻角度为30,60,90°,对3种情况下的钻杆检测结果进行统计,结果见表4。人工检测时,将原视频以16~32倍速度播放,统计钻杆数量。
表4 钻杆统计结果
Table 4 Statistical results of drill pipe

打钻角度/(°)实际钻杆数量人工检测结果图像检测结果3010095996010010210390100100102
分析表4可知,人工检测经常受人员体力影响,识别率可能随时间的延长而降低,而图像检测不受体力等因素影响,识别更稳定,但也存在误识别的现象。现阶段,图像检测识别率并不完全高于人工检测,还需不断对识别过程进行优化,以降低误检率。
最后在河南平煤集团八矿搭建的钻杆统计平台对基于改进ResNet网络的井下钻杆计数方法进行验证,累计卸钻杆1 900次,平均钻杆统计精度为97%。
4 结论
(1) 提出了一种基于改进ResNet网络的井下钻杆计数方法,采用ResNet-50网络建立图像分类模型,并结合线性学习率预热和基于Logistic曲线的学习率衰减策略进行学习率更新。对比分析结果表明,与传统学习率更新策略相比,预热+衰减的更新策略效果最好,模型分类准确率为89%。
(2) 利用积分法对图像分类置信度进行滤波,有效降低了神经网络模型训练结果的误差。实际应用结果表明,基于改进ResNet网络的井下钻杆计数方法的平均精度为97%。
(3) 通过图像分类方法检测钻杆数量,实质是通过图像识别工人卸杆动作来统计钻杆数量,若图像中包含卸杆动作而实际并未卸杆,则会造成误统计的情况。对于如何避免此类误识别情况,今后还需要深入研究。
参考文献(References):
[1] BONDARENKO V,KOVALEVSKA I, ASTAFIEV D,et al.Examination of phase transition of mine methane to gas hydrates and their sudden failure-percy bridgman's effect[J]. Solid State Phenomena,2018,277:137-146.
[2] 宁小亮.煤与瓦斯突出预警技术研究现状及发展趋势[J].工矿自动化,2019,45(8):25-31.
NING Xiaoliang.Research status of early warning technology of coal and gas outburst and its development trend[J].Industry and Mine Automation,2019,45(8):25-31.
[3] SUI D,SUKHOBOKA O, AADNØY B S.Improvement of wired drill pipe data quality via data validation and reconciliation[J]. International Journal of Automation and Computing,2018,15(5):625-636.
[4] 刘勇,何岸,魏建平,等.水射流卸压增透堵孔诱因及解堵新方法[J].煤炭学报,2016, 41(8):1963-1967.
LIU Yong, HE An,WEI Jianping,et al.Plugging factor and new plugging method to hydraulic relieving stress[J].Journal of China Coal Society,2016,41(8):1963-1967.
[5] 高珺.煤矿井下钻孔深度检测技术研究[J].煤炭科学技术,2016,44(4):106-109.
GAO Jun.Study on drilling depth detection technology of underground coal mine[J].Coal Science and Technology,2016,44(4):106-109.
[6] 仇海生,孙波,杨春丽.随钻钻孔深度的声学测量技术实验研究[J].世界科技研究与发展,2015,37(4):338-341.
QIU Haisheng,SUN Bo,YANG Chunli. Experimental study on acoustic measurement technique of drilling depth[J].World Sci-Tech R & D,2015,37(4):338-341.
[7] 路拓,刘盛东,王勃,等.深孔钻孔深度的弹性波测量方法[J].地球物理学进展,2015,30(5):2176-2180.
LU Tuo,LIU Shengdong,WANG Bo,et al. Measurement of deep drilling depth using elastic wave[J].Progress in Geophysics,2015,30(5):2176-2180.
[8] 董立红,王杰,厍向阳.基于改进Camshift算法的钻杆计数方法[J].工矿自动化,2015,41(1):71-76.
DONG Lihong, WANG Jie, SHE Xiangyang. Drill counting method based on improved Camshift algorithm[J].Industry and Mine Automation,2015, 41(1):71-76.
[9] 彭业勋.煤矿井下钻杆计数方法研究[D].西安:西安科技大学,2019.
PENG Yexun. Research on the counting method of underground drill pipe in coal mine [D]. Xi'an:Xi'an University of Science and Technology,2019.
[10] 黄一鸣,雷航,李晓瑜.量子机器学习算法综述[J].计算机学报,2018,41(1):145-163.
HUANG Yiming,LEI Hang,LI Xiaoyu.A survey on quantum machine learning[J]. Chinese Journal of Computers,2018,41(1):145-163.
[11] 张钢,田福庆,梁伟阁,等.基于多尺度AlexNet网络的健康因子构建方法[J].系统工程与电子技术,2020,42(1):245-252.
ZHANG Gang,TIAN Fuqing,LIANG Weige,et al.Construction method of bearing health indicator based on multi-scale AlexNet network[J].Systems Engineering and Electronics,2020,42(1):245-252.
[12] 庄连生,吕扬,杨健,等.时频联合长时循环神经网络[J].计算机研究与发展,2019,56(12): 2641-2648.
ZHUANG Liansheng,LYU Yang,YANG Jian, et al.Long term recurrent neural network with state-frequency memory[J].Journal of Computer Research and Development,2019,56(12):2641-2648.
[13] WAN J, YILMAZ A, YAN L. DCF-BoW:Build match graph using bag of deep convolutional features for structure from motion[J]. IEEE Geoscience and Remote Sensing Letters,2018,15(12):1847-1851.
[14] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,Las Vegas,2016.
[15] HOSSEINI E A, NGUYEN K P, JOINER W M. The decay of motor adaptation to novel movement dynamics reveals an asymmetry in the stability of motion state-dependent learning[J]. PLoS Computational Biology, 2017,13(5):e1005492.