0 引言
煤矿重大事故中57.3%为瓦斯事故，瓦斯灾害已经成为煤矿第一大灾害[1]，因此，及时准确地预测瓦斯浓度具有重要意义。学者们提出了许多有关瓦斯浓度的预测方法。目前，用时间序列管理理论对矿井瓦斯浓度进行预测分析的方法主要有基于ARIMA[2]、神经网络[3]、小波变换[4]、Lyapunov指数算法[5]、灰色系统法[6]、支持向量机[7]、混沌粒子群神经网络[8]、最小二乘支持向量机[9]等方法。还有一些学者将2种分析方法组合起来进行时间序列的预测，诸如基于IABC-RBF算法和小波分析[10]、基于ARIMA与BP组合模型[11]、基于ARIMA-GM模型[12]、基于独立成分分析和K-最近邻法[13]、优化广义回归神经网络[14]等的方法。上述预测方法各有其优点与不足，或算法复杂,或预测步长较短,或不易操作。
针对现有预测方法存在的问题，本文以综采工作面瓦斯浓度历史监测数据分析为基础，根据瓦斯浓度历史监测数据的随机性与时序性，提出了一种基于ARIMA+GARCH组合模型的综采工作面瓦斯数据时间序列预测方法。首先将瓦斯浓度历史监测数据集看作是一个非平稳的随机时间序列，运用统计学R语言对该随机序列建立ARIMA预测模型。在预测模型的可靠性通过检验后，针对ARIMA模型在预测过程中存在的均值回归问题，采用GARCH模型模拟ARIMA产生的拟合残差，并将模拟出的结果作为ARIMA中预测的噪声项，以此优化预测效果，提高瓦斯浓度预测精度。
1 ARIMA模型的构建
1.1 数据的平稳化检验与处理
实现数据平稳的方法主要有差分法、对数法、自相关分析图法、百分比变动法和幂变换法等[15]。考虑到瓦斯浓度数据在正常情况下变动很小，符合差分法的适用原则，因此本文采用差分法。
差分法是克服相关序列相关性的有效方法，分为一阶差分法和广义差分法(广义差分法又名迭代法)。一阶差分就是离散函数中连续相邻两项之差。当自变量从x变到x+1时，函数y=y(x)的改变量Δyx=y(x+1)-y(x)(x=0，1，…),称为函数y(x)在点x的一阶差分，记为Δyx=yx+1-yx。
要使瓦斯浓度监测数据形成的随机时间序列{Yt}平稳化，可对该随机时间序列进行差分处理，在差分的结果上可以继续进行差分，d次差分方程表示如下：
(1)
式中：B为延迟算子，表示时间序列的时间指标;Wt为差分后的平稳数列。
一般情况下，瓦斯浓度监测数据的一阶差分平稳随机过程就可以满足建立ARIMA模型的要求，不用进行二次或多次差分。
原数列及差分处理后的数列可以通过作图来观测是否平稳，也可用增强的Dickey-Fuller(ADF)方法检验随机过程是否平稳。
1.2 模型参数的估计
ARIMA模型中的参数为p,d,q,其中p代表AR模型(自回归模型)的阶数，q代表MA模型(滑动平均模型)阶数，d代表差分次数。实际应用中，d一般取1，不超过2。
瓦斯浓度监测数据随机时间序列Wt如式(2)所示。
(2)
式中：φi为自回归过程的权数；et为白噪声过程；θj为滑动平均过程权数。
采用最小二乘法对φi及θj的值进行估计，将估计值代入式(3)，并转化为et=et(φi,θj)的形式。
(3)
1.3 模型的评价
评价预测模型是否合适的依据是预测值与实际值拟合程度的高低，若拟合程度较高，则表明模型可以用于预测；反之，则需要对模型的原参数进行修正。
在AR、MA及ARIMA随机过程中,随机扰动et被假设为白噪声过程，因此，必须用检验模型拟合残差随机过程来判断合理性，残差如式(4)所示。基于瓦斯浓度随机过程Yt可得到起始点直到t时刻的瓦斯体积分数的历史监测数据，即Y1，Y2，…，Yt。要预测未来l期的瓦斯体积分数Yt+1，则预测起点为时间t，预测的前置时间为l，用
表示瓦斯体积分数监测数据随机过程的预测值。
(4)
(5)
(6)
式中：
为t时刻瓦斯体积分数预测值；ψ为权重，且ψ0=-1；φj为自回归项的系数。
模型具体评价过程：判断残差序列
是否为独立于随机过程Yt的新息项，若大多在0上下波动，且不存在任何时间序列趋势，则说明预测模型拟合程度较高。
2 GARCH模型表示
GARCH(Generalized AutoRegressive Conditional Heteroskedasticity)模型又称为“广义自回归条件异方差模型”。ARIMA模型在预测时，由于过程的残差序列不相关，存在厚尾分布和波动集群(即高阶相关结构)，滑动平均项无法直接得到，所以，需要对ARIMA模型的拟合残差建立相应的GARCH模型，将GARCH模型模拟出的新随机过程作为ARIMA模型预测的误差项对瓦斯浓度进行预测。
GARCH(u，v)模型如式(7)所示。
(7)
式中：
为t时刻时条件方差的估测值；ω、α、β为未知参数；u为ARCH模型的阶数；rt为拟合后的时间序列；v为GARCH模型的阶数；εt为t时刻的残差项。
3 基于ARIMA+GARCH组合预测模型的瓦斯浓度预测精度判断
ARIMA模型通过寻求瓦斯浓度数据与预测误差之间的线性方程来对瓦斯浓度进行预测，但该模型无法得到误差项，导致单独使用ARIMA模型进行预测可能会有较大偏差。
用GARCH模型处理ARIMA模型的残差序列，使得残差序列中每一时刻的对应数值均与ARIMA模型预测公式中的噪声项一一对应，可以减小预测误差。为此，利用ARIMA+GARCH组合预测模型来提高瓦斯浓度的预测精度。
判断预测精确度的指标主要有4个：平均绝对误差(Mean Absolute Deviation，MAD)、相对百分误差绝对值(Mean Absolute Percent Error，MAPE)、标准差(Standard Deviation Error，SDE)、均方误差(Mean Squared Error，MSE)，它们的计算公式如下所示：
(8)
(9)
(10)
(11)
式中n为时间序列中数据样本的个数。
4 实例分析
4.1 ARIMA模型的搭建
4.1.1 瓦斯数据来源与处理
瓦斯实验数据样本来自陕西某矿井下综采工作面，选取2018年8月21—24日4天，每小时4个时点的瓦斯浓度监测实时数据作为样本实验数据。其中，选取2018-08-21T00:00—2018-08-23T23:50的288(4×24×3)个瓦斯浓度监测数据对建立的预测模型进行拟合；选取2018-08-24T00:00—11:50作为预测区间，使用该区间内的96(4×24×1)个瓦斯浓度数据验证预测模型的精确度。
首先对上述288个瓦斯浓度监测数据进行一阶差分，使瓦斯时间序列平稳化，工作面瓦斯体积分数一阶差分时间序列如图1所示。
图1 工作面瓦斯体积分数一阶差分时间序列
Fig.1 First-order difference time series of gas concentration on working face
从图1可看出，瓦斯时间序列Wt的数值在0附近均匀分布，序列的数值随着时间的滞后上下波动，且没有数值增大或数值减小的趋势。由此可以认为，经过一阶差分后的Wt是平稳的，符合ARIMA模型预测的基本要求，即一阶差分后的Wt所对应的瓦斯浓度预测模型为ARIMA(p,1,q)。
4.1.2 瓦斯浓度预测模型的阶数确定
拓展的自相关法(EACF)针对大小适度的样本容量具有不错的样本性质，可用其对ARIMA(p,1,q)模型随机过程进行定阶。
汇总瓦斯时间序列Wt的EACF信息，结果见表1。若Wt,k,j的j+1阶滞后样本相关程度大于
则第k行和第j列元素用符号X表示；若Wt,k,j样本自相关系数逐渐服从分布N(0,1/n-k-j)，是近似MA(j)过程，则用0表示。由表1可知,从第4行、第6列的数字0开始，其右侧及下方的数字均为0，这代表随机过程ARIMA(p,1，q)中的p=4,q=6，于是得到Wt的预测模型为ARIMA(4,1,6)。
表1 瓦斯体积分数一阶差分时间序列Wt的EACF
Table 1 EACF of the first-order differential time seriesWtof gas concentration
4.1.3 瓦斯浓度预测模型的参数估计
使用R语言可求得式(3)中φ和θ的最小取值，φ值为ARIMA模型中AR项权重预估值，θ为ARIMA模型中MA项的权重预估值，见表2。
表2 ARIMA(4,1,6)模型中的具体参数
Table 2 Specific parameters of the ARIMA (4,1,6) model
Wt可表示为
Wt=0.324 2Wt-1+0.251 2Wt-2-0.295 4Wt-3-0.121 0Wt-4+et+0.429 8et-1-0.048 4et-2-0.108 0et-3+0.047 5et-4-0.256 8et-5-
0.032 4et-6
(12)
用差分
的形式替换一阶差分时间序列中的Wt，并进行等式左右移项，即可得到Yt的表达式为
Yt=1.324 2Yt-1+0.073 0Yt-2-0.546 6Yt-3+
0.121 6Yt-4-0.121 0Yt-5+et+0.429 8et-1-0.048 4et-2-0.108 0et-3+0.047 5et-4-
0.256 8et-5-0.032 4et-6
(13)
4.1.4 瓦斯浓度预测模型的精确度评价
在运用式(13)进行数据拟合时，考虑到公式中既有观测序列又有噪声项，而噪声项不能直接观测得到，因此须将式(13)转换为式(5)的形式。
取ψ0=-1，通过不断迭代后，可以得到式(5)中的ψ权重，最终的运算结果可表示为
0.429 8Yt-1(l)-0.048 4Yt-2(l)-
0.108 0Yt-3(l)+0.047 5Yt-4(l)-
0.256 8Yt-5(l)-0.032 4Yt-6(l)
(14)
利用式(14)对瓦斯体积分数监测数据进行拟合，结果如图2所示。
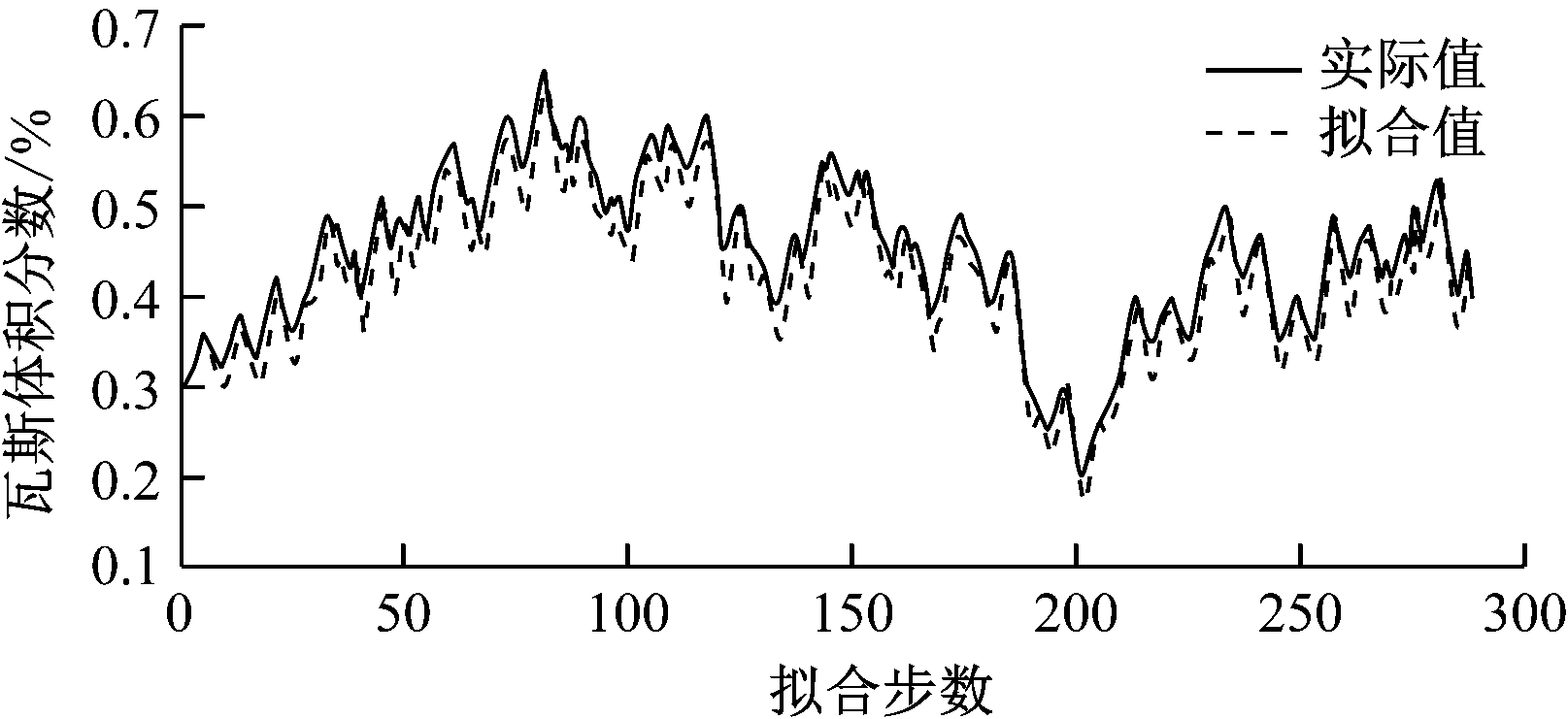
图2 瓦斯体积分数实际值与拟合值对比
Fig.2 Comparison of actual and fitted values of gas concentration
从图2可看出，瓦斯实际值与拟合值的趋势基本一致，表明拟合程度较高，选取的瓦斯浓度预测模型ARIMA(4,1,6)是合适的。
4.2 残差序列的GARCH模型处理
4.2.1 GARCH模型的识别
对ARIMA(4,1,6)模型的拟合残差序列进行GARCH模型识别，然后同样运用EACF方法计算拟合的残差随机过程平方值，结果见表3。
表3 ARIMA(4,1,6)模型残差序列平方值的样本EACF
Table 3 Sample EACF of the ARIMA(4,1,6) model residual sequence squared value
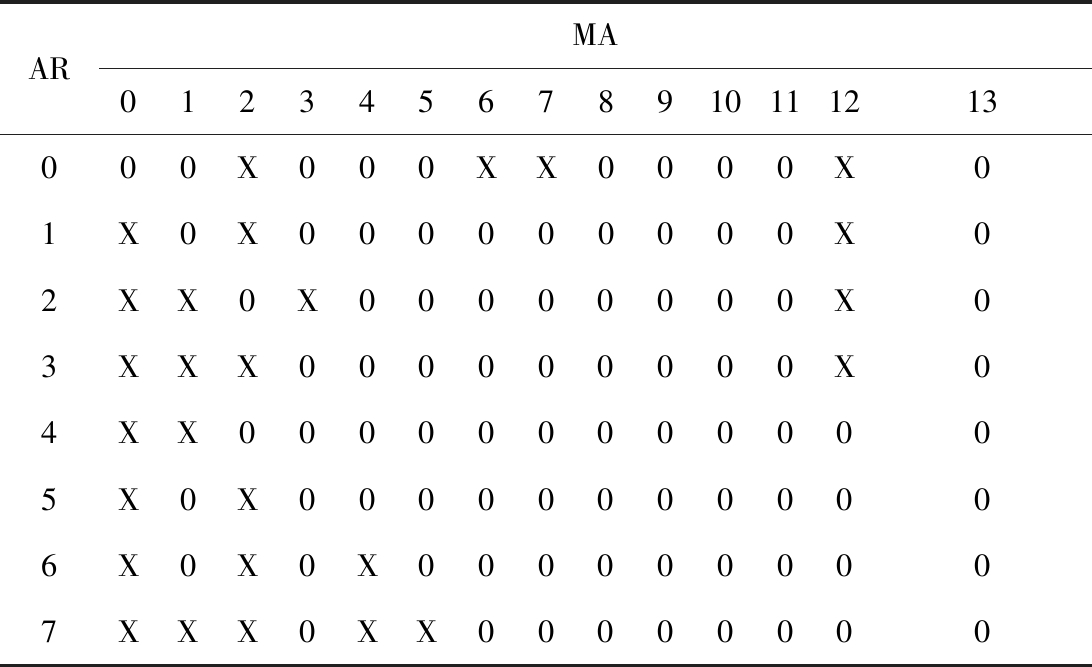
从表3可看出，从第4行、第3列的数字0开始，其右侧及下方的数字绝大部分为0，且max(u，v)= max(4，3)，这代表GARCH(u，v)模型中的阶数u=3，v=4，即残差随机过程为GARCH(3,4)。
4.2.2 GARCH模型参数的确定
GARCH模型的参数可使用极大似然法(Maximum Likelihood Estimate，MLE)进行估算，式(7)的极大似然可表示为
L(ω,α,β)=
(15)
用式(15)对GARCH(3,4)模型中的参数进行估算，估算结果见表4。
表4 GARCH(3,4)模型参数的估计值
Table 4 Estimated values of parameters of the GARCH(3,4) model
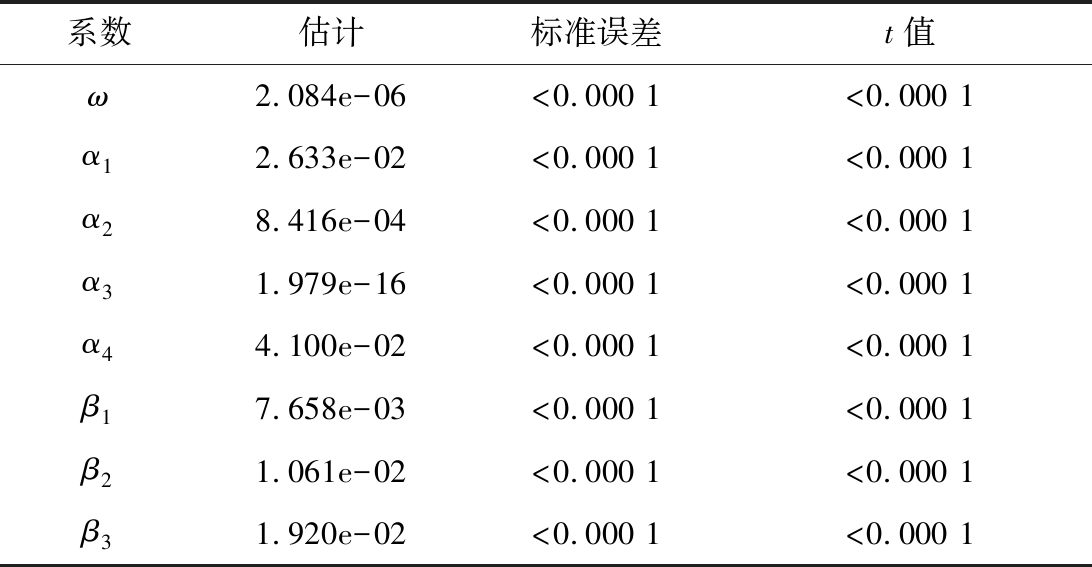
将表4中的参数估计值代入式(7)，运用R语言进行计算，得到GARCH模型的表达式为
(16)
4.3 瓦斯浓度预测组合模型的预测过程及效果评价
使用R语言模拟GARCH模型的随机过程，如图3所示。图3下部为R语言实现的具体编程代码。
图3中的模拟结果即为式(14)中向前1—96期的噪声项，经过迭代运算，可得综采工作面瓦斯体积分数预测值，结果如图4所示。
从图4可看出，ARIMA(4,1,6)+GARCH(3,4)组合模型的预测值的趋势走向与某矿综采工作面瓦斯体积分数实际值的趋势走向基本一致，表明基于ARIMA(4,1,6)+GARCH(3,4)组合模型的预测方法的预测效果较好。
通过式(8)—式(11)计算可得：MAD=0.026 8，MAPE=5.56%，SDE=0.043 6，MSE=0.001 9。4项误差值都很小，表明可以应用ARIMA+GARCH组合模型进行瓦斯浓度未来趋势预测。
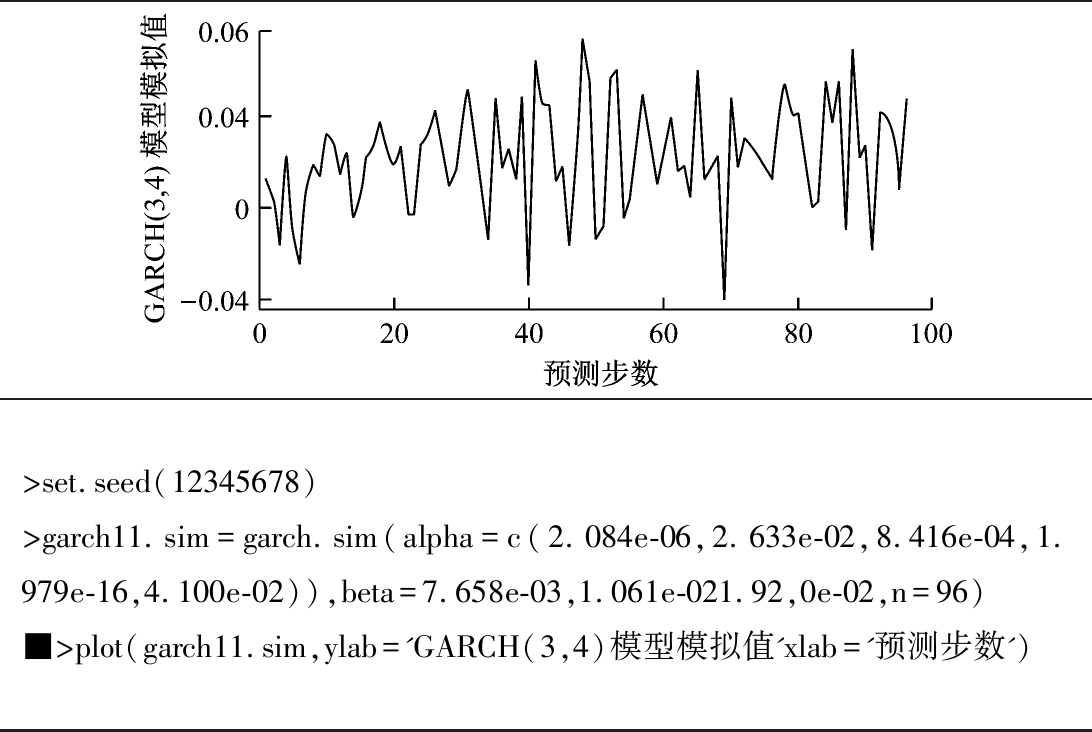
图3 GARCH(3,4)模型模拟结果
Fig.3 Simulation results of the GARCH(3,4) model
图4 瓦斯体积分数预测值与实际值对比
Fig.4 Comparison of predicted and actual values of gas concentration
5 结论
(1) ARIMA模型利用瓦斯浓度实际值与预测误差之间的线性方程来对瓦斯浓度进行预测，但该模型无法得到误差项，这导致单独使用ARIMA模型对瓦斯浓度进行预测可能会有较大偏差。
(2) 用GARCH模型处理ARIMA模型的残差序列，使得残差序列中每一时刻的对应数值均与ARIMA模型预测公式中的噪声项一一对应，可以减小预测误差。
(3) 应用基于ARIMA+GARCH组合模型的瓦斯浓度预测方法对某矿综采工作面瓦斯浓度进行预测，4个判断指标都很小，表明该组合模型预测瓦斯浓度变化趋势的精度较高。
参考文献( References)：
[1] 蓝航,陈东科,毛德兵.我国煤矿深部开采现状及灾害防治分析[J].煤炭科学技术,2016,44(1):39-46.
LAN Hang，CHEN Dongke，MAO Debing.Current status of deep mining and disaster prevention in China[J].Coal Science and Technology,2016,44(1):39-46.
[2] 郭思雯,陶玉帆,李超.基于时间序列的瓦斯浓度动态预测[J].工矿自动化,2018,44(9):20-25.
GUO Siwen，TAO Yufan，LI Chao.Dynamic prediction of gas concentration based on time series[J].Industry and Mine Automation,2018,44(9):20-25.
[3] 张昭昭,乔俊飞,余文.基于动态神经网络的瓦斯浓度实时预测方法[J].控制工程,2016,23(4):478-483.
ZHANG Zhaozhao,QIAO Junfei,YU Wen.Forecasting coalmine gas concentration based on dynamic neural network[J].Control Engineering of China,2016,23(4):478-483.
[4] 程勰.基于小波分析的金融时间序列风险度量值估计方法与实证研究[D].广州：暨南大学,2016.
[5] 韩磊.基于监测技术的采煤工作面瓦斯浓度预测预警[J].山西焦煤科技,2017,41(增刊1):44-48.
HAN Lei.Prediction of gas concentration based on monitoring technology of working face[J].Shanxi Coking Coal Science & Technology,2017,41(S1):44-48.
[6] 刘海燕.深基坑监测数据分析与变形预测研究[D].北京：北京交通大学,2012.
[7] 尹小琴.基于支持向量机的混合时间序列模型的研究与应用[D].沈阳：沈阳工业大学,2016.
[8] 耿越.基于混沌粒子群神经网络的瓦斯浓度预测[J].中国煤炭,2017,43(3):124-129.
GENG Yue.Chaotic PSO-RBFNN in coal mine gas concentration prediction[J].China Coal,2017,43(3):124-129.
[9] 单亚锋,侯福营,付华.基于改进极端学习机的混沌时间序列瓦斯涌出量预测[J].中国安全科学学报,2012,22(12):58-63.
SHAN Yafeng,HOU Fuying,FU Hua.Prediction of chaotic time series of gas emission based on improved extreme learning machine[J].China Safety Science Journal,2012,22(12):58-63.
[10] 刘利强.基于IABC-RBF算法和小波分析的瓦斯时间序列优化预测[D].阜新：辽宁工程技术大学,2015.
[11] 邢浩然,杨应迪.基于ARIMA与BP组合模型的煤矿瓦斯涌出量预测[J].内蒙古煤炭经济,2017(17):3-6.
[12] 吴兵,郭志国,王紫薇.基于ARIMA-GM模型的采掘工作面瓦斯涌出预测[J].煤矿安全,2015,46(11):152-155.
WU Bing，GUO Zhiguo，WANG Ziwei.Gas emission forecasting at heading face based on ARIMA-GM model[J].Safety in Coal Mines,2015,46(11):152-155.
[13] 龚星宇,常心坦,贾澎涛.独立成分分析在瓦斯浓度预测中的应用研究[J].工矿自动化,2015,41(4):82-86.
GONG Xingyu,CHANG Xintan,JIA Pengtao.Application research of independent component analysis in gas concentration prediction[J].Industry and Mine Automation,2015,41(4):82-86.
[14] 付华,刘汀,张胜强,等.基于改进ABC-GRNN模型的煤矿瓦斯浓度预测研究[J].控制工程,2017,24(4):881-887.
FU Hua,LIU Ting,ZHANG Shengqiang,et al.Gas concentration prediction model of coal mine based on improved ABC-GRNN algorithm[J].Control Engineering of China,2017,24(4):881-887.
[15] 马彦龙. 基于时间序列分析的综采工作面瓦斯浓度预测研究[D].西安：西安科技大学,2018.