0 引言
我国煤矿的水文地质条件、矿井充水条件复杂多样,煤矿在生产过程中受到的各种水害威胁十分严重,煤矿防治水工作是矿井生产的难点[1-3]。矿井构造复杂程度是影响水害的重要因素,多数矿井涌(突)水事故与地质构造(尤其是断层与褶皱)有着密切关系。近年来,众多学者对矿井构造复杂程度评价进行了大量研究。魏大勇等[4]采用模糊综合评判方法对恒源煤矿6煤底板构造复杂程度进行评价,阐述了矿井构造复杂程度与矿井突水的耦合关系。李骏等[5]采用分形理论和趋势面分析方法对阳泉二矿矿井构造复杂程度进行了定量分析。施龙青等[6]针对翟镇井田因断裂构造发育而导致频繁突水的现状,提出了断层影响因子的概念,结合统计分析法对矿井构造复杂程度进行了评价。徐文军等[7]选取构造曲率、断层强度、断层密度、断层分形维数等参数,采用层次分析法构建了矿井构造复杂程度评价指标体系,并结合分形理论对煤层构造复杂程度进行了定量化评价。周阳等[8]以基于分形理论的脆弱性指数法评价煤层底板构造复杂程度。舒建生等[9]采用灰色关联分析方法和等性块段综合指数评价方法,对矿井构造复杂程度作出了定量化综合评价和分类。
本文以大屯煤电(集团)有限责任公司徐庄煤矿为例,采用独立性权系数法确定影响矿井构造复杂程度的各指标权重,通过ArcGIS对各指标进行融合分析,从而对矿井构造复杂程度进行定量评价,为矿井涌(突)水危险性预测及水害防治提供重要依据。
1 研究区概况
徐庄煤矿位于江苏省徐州市沛县大屯矿区,是典型的华北型全掩盖式煤田,含煤地层为晚古生代石炭二叠系的太原组、山西组、下石盒子组。含煤20多层,4层可采煤层(7,8,17,21号),总厚度平均为9.95 m。
徐庄煤矿井田位于滕沛复向斜中南部,大部分区域呈一走向北东、倾向北西的单斜构造,倾角为10~36°,平均为17.3°。其北为断层F20,落差超过1 000 m,切割了井田西南部煤层,构成了井田的自然边界。根据勘探、物探与井下采掘的实测资料可知,徐庄煤矿井田内地质构造主要是断层,共有400多条,正断层相对逆断层较为发育,并且多呈束状、枝状分布,断层的倾向主要有北西和北东2组,按照力学性质不同可分为张扭性和压扭性2组,以张扭性为主,大多数为高角度正断层。
矿区由于多次受构造运动的影响,在井田中西部发育形成了不同级别、不同方向的褶皱,其中有魏营背斜、魏营向斜、贾庙西向斜、刘家向斜、陈楼东向斜,如图1所示。
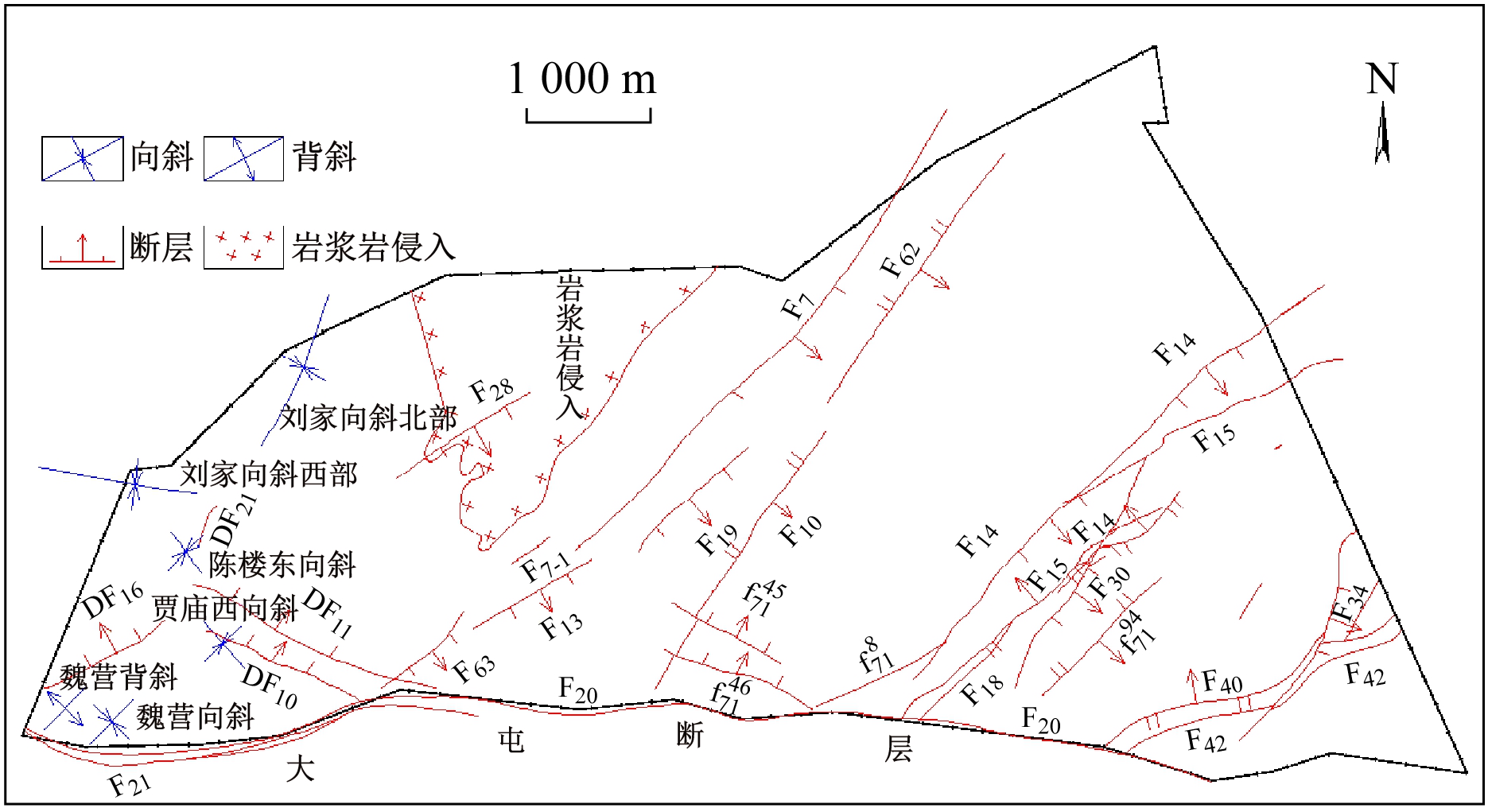
图1 构造纲要
Fig.1 Structural outline
2 基于ArcGIS与独立性权系数法的矿井构造复杂程度定量评价
2.1 评价指标选取
断裂和褶皱是矿井地质构造的重要组成部分,本文对于研究区矿井构造复杂程度的定量评价主要考虑了断裂、褶皱两方面的影响,具体评价指标包括断裂分维值、断层强度指数和褶皱平面变形系数。
2.1.1 断裂分维值
断裂分维值包含断裂条数、延伸长度和相互交叉关系等多方面的变化关系,可作为一个综合性指标,充分反映断裂构造的发育程度[10]。断裂分维值和断裂长度、小断层和分支断层数量呈正比关系,即断裂分维值越大,断裂构造越发育。采用滑动窗口法[11]计算矿井区域的断裂分维值,运用不同边长正方形网格覆盖研究区的断裂区域,网格数目随着正方形网格边长和网格密集程度变化而变化。
(1)
式中:N(ε)为网格数目;ε为正方形网格边长;C为倍率;D为断裂分维值。
对式(1)两边同取对数可得
lgN(ε)=-Dlgε+A
(2)
式中A为待定常数。
根据计算所得的矿井区域断裂分维值绘制断裂分维值等值线,如图2所示。由图2可知,研究区断裂分维值为1.1~1.9,变化范围不大,分布趋势整体为东部高西部低,东部采区断裂分维值为1.5~1.9,西部采区断裂分维值为1.1~1.8,且与断裂发育密度有很好的对应关系,断裂发育聚集区域的断裂分维值比较大;在矿井东部的中心部位,断层F14以浅区域断裂分维值较大,达1.8以上,至-700 m以深,断裂分维值减小,在1.6以下,但整体还是较大,即矿井在向深部水平开拓生产过程中,可能会存在较多小断层,特别是F7,F622条大型断层附近;在矿井西部采区,断裂分维值从南向北呈减小趋势,靠近南部断层F21及陈楼东向斜附近断裂分维值大于1.8。由此可见,研究区的东部采区及西部采区中南部的断裂分维值较大且密集,尤其在F14,F15,F21等大型断层附近断裂分维值达到最大。

图2 断裂分维值等值线
Fig.2 Fault fractal dimension value isoline
目前徐庄煤矿主要开采的是东部和浅部区域,西部和深部地区尚未开采。对已开采的东部地区涌(突)水点信息进行整理,将涌(突)水点坐标投影于图2上。可看出断裂分维值为1.6~1.7的区域内分布3个涌(突)水点,占比21.43%,断裂分维值为1.7~1.8的区域内分布5个涌(突)水点,占比35.71%,断裂分维值为1.8~1.9的区域内分布6个涌(突)水点,占比42.86%,表明断裂分维值越大,涌(突)水点分布越密集。
2.1.2 断层强度指数
断层强度指数是指单位面积内所有断层的落差与水平延伸长度的乘积之和:
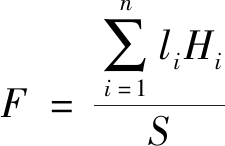
(3)
式中:F为断层强度指数;li为第i(i=1,2,…,n,n为断层条数)条断层水平延伸长度,m;Hi为第i条断层落差,m;S为统计面积,万m2。
采用滑动窗口法对研究区断层强度指数进行统计,并绘制断层强度指数等值线,如图3所示。由图3可知,断层强度指数为0.02~0.21;由于断层F7,F14和F15落差较大,断层强度指数受这几条断层影响较大,其等值线形态在矿井中北部大致沿断层位置呈条带状分布(断层F7附近区域(约在10勘探线深部)断层强度指数最大值达0.21),在矿井东部大致沿断层F14,F15呈条带状分布(断层强度指数最大值达0.16);矿井西部(约在4勘探线以西)断层强度指数基本小于0.10。将已开采的东部地区涌(突)水点坐标投影于图3上,可看出断层强度指数为0.02~0.07的区域内分布3个涌(突)水点,占比21.43%,断层强度指数为0.07~0.12的区域内分布4个涌(突)水点,占比28.57%,断层强度指数为0.12~0.16的区域内分布7个涌(突)水点,占比50.0%,表明断层强度指数越大,涌(突)水点分布越密集。
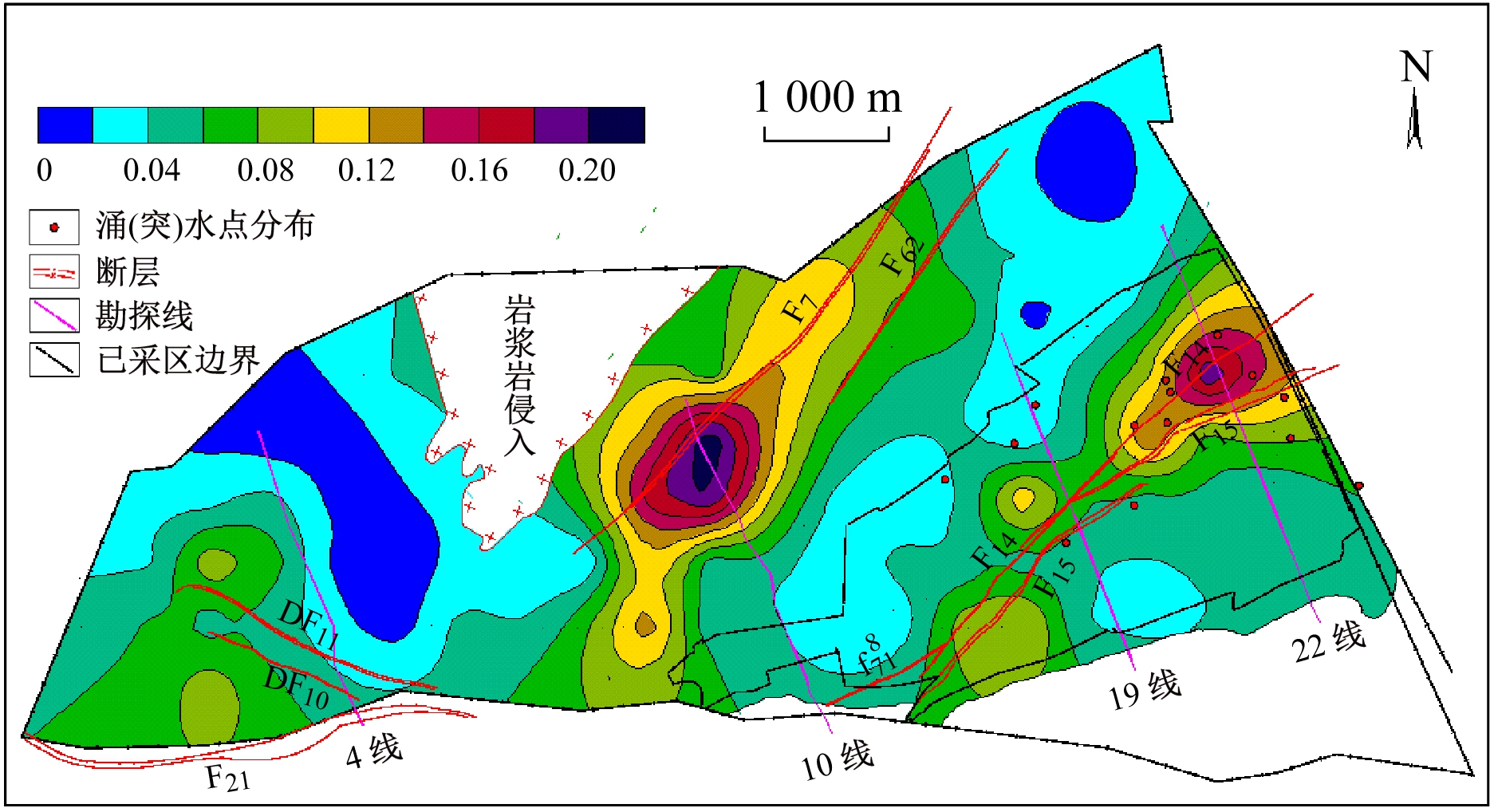
图3 断层强度指数等值线
Fig.3 Fault intensity index isoline
2.1.3 褶皱平面变形系数
褶皱平面变形系数定量表征了构造应力场下层状岩层发生褶皱变形程度,与褶皱发育程度存在较好对应关系[12],通过褶皱平面变形系数的分布可直观反映井田范围内褶皱发育程度。
(4)
式中:Kp为褶皱平面变形系数;h为相邻2条等高线标高差,m;L0为计算单元中心相邻2条等高线间的水平距离,m;L1为靠近计算单元中心的等高线在单元内的实际长度,m;L2为计算单元中心轮廓附近的等高线在单元内的割线长度,m。
统计研究区褶皱平面变形系数,并绘制褶皱平面变形系数等值线,如图4所示。由图4可知,研究区褶皱平面变形系数为0.19~0.62;受西部采区几个大的褶皱影响,矿井西部褶皱平面变形系数高于东部,在刘家向斜附近(约在4勘探线的浅部与西部)的褶皱平面变形系数最大,超过0.50,矿井东部采区褶皱发育较弱,约在10勘探线以东区域褶皱平面变形系数基本小于0.4,仅在7199工作面等小区域内褶皱平面变形系数达0.48。将已开采的东部地区涌(突)水点坐标投影于图4上,可看出褶皱平面变形系数为0.20~0.30的区域内分布3个涌(突)水点,占比21.43%,褶皱平面变形系数为0.30~0.40的区域内分布2个涌(突)水点,占比14.28%,褶皱平面变形系数为0.40~0.48的区域内分布9个涌(突)水点,占比64.29%,表明褶皱平面变形系数越大,涌(突)水点分布越密集。
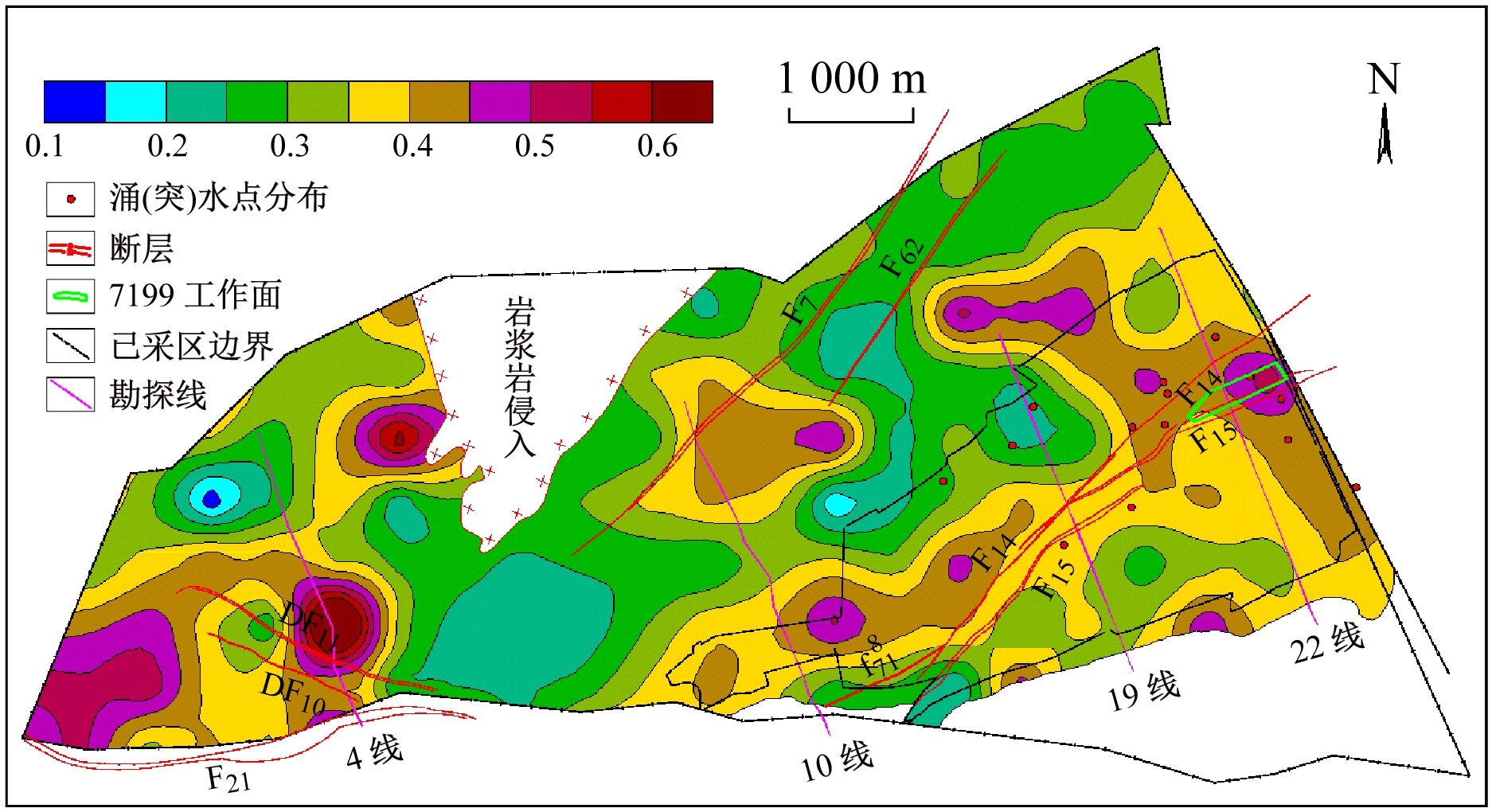
图4 褶皱平面变形系数等值线
Fig.4 Folding plane deformation coefficient isoline
2.2 数据归一化处理
为消除各评价指标不同量纲数据对矿井构造复杂程度评价结果的影响,需要对各评价指标原始数据进行归一化处理。考虑到本文选取的断裂分维值、断层强度指数、褶皱平面变形系数这3个评价指标与矿井构造复杂程度之间的正相关关系[13],采用最小-最大标准化方法对数据进行归一化处理[14]。
2.3 权重确定
断裂分维值、断层强度指数、褶皱平面变形系数这3个评价指标之间存在信息重叠部分[15-16],若直接将这些评价指标用于矿井构造复杂程度评价,则会降低评价结果的准确度。因此,采用独立性权系数法确定各评价指标权重。
计算评价指标Xj(j=1,2,3)与其他评价指标之间的复相关系数:
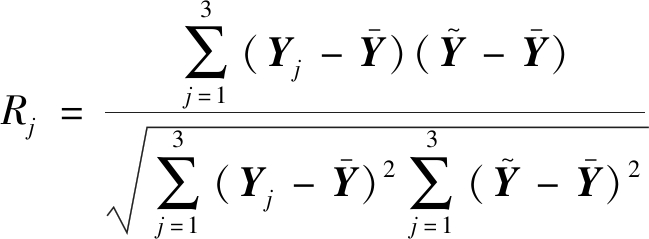
(5)
式中:Yj为评价指标矩阵;![]() 为除去Xj的其他评价指标平均值矩阵;
为除去Xj的其他评价指标平均值矩阵;![]() 为除去Xj的其他评价指标矩阵。
为除去Xj的其他评价指标矩阵。
复相关系数越大,表明评价指标Xj与其他评价指标之间共线性关系越强,即重复信息越多,则该评价指标的权重也越小[16]。考虑到复相关系数与权重之间呈负相关关系,选取复相关系数的倒数作为评分,经过标椎化处理计算,可得各评价指标权重:
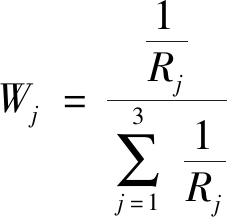
(6)
断裂分维值、断层强度指数、褶皱平面变形系数评价指标的权重见表1。
表1 评价指标权重
Table 1 Evaluation index weight

2.4 矿井构造复杂程度定量评价
将各评价指标归一化后的数据导入ArcGIS中,建立断裂分维值、断层强度指数和褶皱平面变形系数的归一化专题图。将通过独立性权系数法得到的权重分别赋予3个评价指标,应用ArcGIS对各评价指标的归一化专题图进行融合计算,得到矿井构造复杂程度定量评价模型:
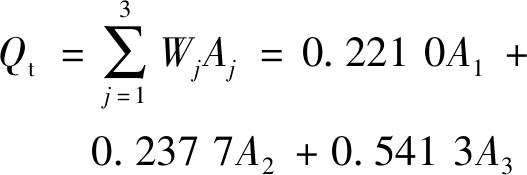
(7)
式中:Qt为评价指数;Aj为第j个评价指标的归一化值。
根据矿井构造复杂程度定量评价模型,通过对Qt进行统计分析,运用Natural Breaks(Jenks)(自然间断分级法)进行分级,确定分级阈值分别为0.468 1,0.525 4,0.580 7,见表2。Qt越大,表明矿井构造复杂程度越大。
表2 矿井构造复杂程度分级
Table 2 Mine structure complexity classification

依据分级阈值将研究区划分为复杂构造区、较复杂构造区、中等复杂构造区和简单构造区4个区域,如图5所示。由图5可知,复杂构造区主要分布在矿井东部(大致沿断层F14,F15两侧呈条带状区域分布)、矿井中部(约在10勘探线深部)、矿井西南角(约在4勘探线以西)及岩浆岩区域西北侧局部,矿井东部断裂分维值较大,矿井中部断层强度指数较大,矿井西南角断裂分维值和褶皱平面变形系数较大,岩浆岩区域西北侧局部褶皱平面变形系数较大;较复杂构造区主要集中在矿井中北部;中等复杂构造区主要分布在矿井西部靠近岩浆岩侵入体区域及10勘探线与19勘探线之间的北部;简单构造区主要分布在矿井西北部。
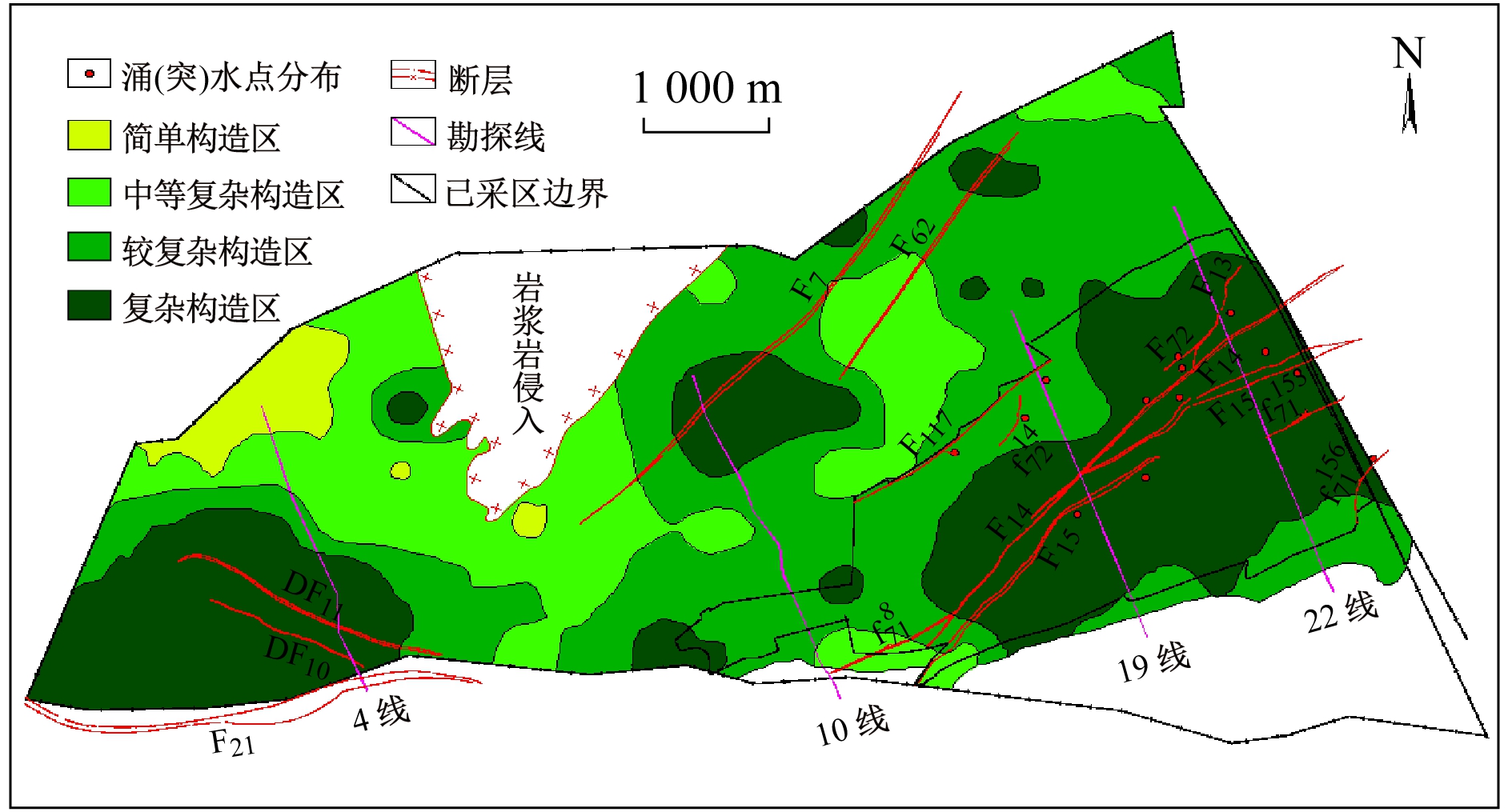
图5 矿井构造复杂程度分区
Fig.5 Mine structure complexity zoning
3 矿井构造复杂程度与涌(突)水耦合分析
由图2—图4可知,断裂分维值、断层强度指数和褶皱平面变形系数越大,涌(突)水点分布越密集,表明涌(突)水点分布密集程度与评价指标之间存在正相关性。由图5可知,涌(突)水点分布于复杂和较复杂构造区内,其中较复杂构造区内有3个涌(突)水点,占比21.43%,复杂构造区内涌(突)水点高达11个,占比78.57%,表明矿井涌(突)水与构造复杂程度之间存在明显的耦合关系,即矿井构造复杂程度越大,涌(突)水点分布越密集;涌(突)水点主要分布在断层F14,F15附近,分布方向与F14,F15走向一致,表明涌(突)水点位置和断层联系密切,其原因是断层附近构造裂隙发育和地下水资源富集。
4 结论
(1) 研究区断裂分维值为1.1~1.9,总体呈东高西低的分布趋势,在F14,F15,F21等大型断层附近断裂分维值达到最大;断层强度指数为0.02~0.21,受大型断层影响,其等值线形态在矿井中北部大致沿断层F7呈条带状分布,在矿井东部大致沿断层F14,F15呈条带状分布;褶皱平面变形系数为0.19~0.62,矿井西部褶皱平面变形系数高于东部,在刘家向斜附近(约在4勘探线的浅部与西部)的褶皱平面变形系数最大,东部采区褶皱发育较弱。结合已开采的东部地区涌(突)水点空间分布可知,断裂分维值、断层强度指数和褶皱平面变形系数越大,涌(突)水点分布越密集。
(2) 采用独立性权系数法确定影响矿井构造复杂程度的断裂分维值、断层强度指数和褶皱平面变形系数的权重,利用ArcGIS建立矿井构造复杂程度定量评价模型,将研究区划分为复杂构造区、较复杂构造区、中等复杂构造区和简单构造区4个区域。研究区以复杂构造为主,构造复杂程度主要受控于大型断层和褶皱。
(3) 通过分析已开采东部地区涌(突)水点的空间分布,发现涌(突)水点主要位于矿井复杂和较复杂构造区内,矿井构造复杂程度越大,涌(突)水点分布越密集,表明矿井构造对矿井涌(突)水具有明显的控制作用。
参考文献(References):
[1] 李东东.红柳林煤矿2-2煤顶板涌(突)水危险性评价[D].西安:西安科技大学,2017.
LI Dongdong.Evaluation of water bursting risk from the roof of 2-2coal seam in Hongliulin Coal Mine[D].Xi'an:Xi'an University of Science and Technology,2017.
[2] 董书宁,虎维岳.中国煤矿水害基本特征及其主要影响因素[J].煤田地质与勘探,2007,35(5):34-38.
DONG Shuning,HU Weiyue.Basic characteristics and main controlling factors of coal mine water hazard in China[J].Coal Geology and Exploration,2007,35(5):34-38.
[3] 杜春蕾,张雪英,李凤莲.改进的CART算法在煤层底板突水预测中的应用[J].工矿自动化,2014,40(12):52-56.
DU Chunlei,ZHANG Xueying,LI Fenglian.Application of improved CART algorithm in prediction of water inrush from coal seam floor[J].Industry and Mine Automation,2014,40(12):52-56.
[4] 魏大勇,王飞,许进鹏,等.基于分形与模糊综合评价法的矿井突水危险性评价[J].煤矿安全,2013,44(8):184-186.
WEI Dayong,WANG Fei,XU Jinpeng,et al.Risk evaluation of mine water inrush based on the fractal and fuzzy comprehensive evaluation method[J].Safety in Coal Mines,2013,44(8):184-186.
[5] 李骏,姜波,李明,等.阳泉二矿断裂构造复杂程度与趋势面分析[J].煤炭技术,2016,35(9):95-98.
LI Jun,JIANG Bo,LI Ming,et al.Analysis of complex degree of fault structure and trend surface in Yangquan No.2 Coal Mine[J].Coal Technology,2016,35(9):95-98.
[6] 施龙青,王丹丹,李常松,等.翟镇井田断裂构造分布特征定量化分析[J].中国科技论文,2015,10(9):1080-1083.
SHI Longqing,WANG Dandan,LI Changsong,et al.Quantitative analysis of fracture structure characteristics in Zhaizhen Coal Mine[J].China Sciencepaper,2015,10(9):1080-1083.
[7] 徐文军,张莎莎,吴财芳,等.基于层次分析法的煤储层构造复杂程度定量评价[J].河南理工大学学报(自然科学版),2019,38(2):20-26.
XU Wenjun,ZHANG Shasha,WU Caifang,et al.Quantitative assessment of structure complexity of coal reservoir based on analytical hierarchy process[J].Journal of Henan Polytechnic University(Natural Science),2019,38(2):20-26.
[8] 周阳,陈江峰,肖新成,等.断裂构造分形及其在矿山突水评价中的应用[J].中国地质灾害与防治学报,2017,28(1):115-120.
ZHOU Yang,CHEN Jiangfeng,XIAO Xincheng,et al.Fractal analysis of fault structures and its application in the assessment of water burst[J].The Chinese Journal of Geological Hazard and Control,2017,28(1):115-120.
[9] 舒建生,贾建称,王跃忠,等.地质构造复杂程度定量化评价——以涡北煤矿为例[J].煤田地质与勘探,2010,38(6):22-26.
SHU Jiansheng,JIA Jiancheng,WANG Yaozhong,et al.Quantitative evaluation of geological structure complexity: with Guobei Coal Mine as example[J].Coal Geology and Exploration,2010,38(6):22-26.
[10] 彭涛.淮北煤田断裂构造系统及其形成演化机理[D].淮南:安徽理工大学,2015.
PENG Tao.The fault system and its evolution mechanism of Huaibei coalfield[D].Huainan:Anhui University of Science and Technology,2015.
[11] 黄伟.钱营孜煤矿构造发育特征及复杂程度定量评价[D].淮南:安徽理工大学,2011.
HUANG Wei.Development characteristics of geological structure and quantitative evaluation of complex degree in Qianyingzi Coal Mine[D].Huainan:Anhui University of Science and Technology,2011.
[12] 宣良瑞.卧龙湖煤矿K3砂岩富水性评价及8101面涌水水源分析[D].淮南:安徽理工大学,2014.
XUAN Liangrui.The evaluation on the water abundance of K3 sandstone and the analysis on the source of water inrush of 8101 working face in Wolonghu Coal Mine[D].Huainan:Anhui University of Science and Technology,2014.
[13] 施龙青,滕超,韩进,等.基于层次分析法-系统聚类分析的井田构造复杂程度评价[J].中国科技论文,2015,10(21):2550-2554.
SHI Longqing,TENG Chao,HAN Jin,et al.Evaluation of mine field structure complexity based on analytical hierarchy process and hierarchical cluster analysis[J].China Sciencepaper,2015,10(21):2550-2554.
[14] 王汉斌.基于ArcGIS的首旺煤矿突水水害危险性评价[D].北京:中国地质大学(北京),2017.
WANG Hanbin.Risk assessment of water inrush from coal mine of the Shouwang Colliery based on ArcGIS[D].Beijing:China University of Geosciences(Beijing),2017.
[15] 李飞,杨滨滨,张金陵,等.矿井断层构造复杂程度的GIS与熵值耦合评价研究[J].中国煤炭地质,2014,26(8):60-63.
LI Fei,YANG Binbin,ZHANG Jinling,et al.GIS and entropy coupling evaluation on mine fault structural complexity[J].Coal Geology of China,2014,26(8):60-63.
[16] 张淑莹,胡友彪,邢世平.基于独立性权-灰色关联度理论的突水水源判别[J].水文地质工程地质,2018,45(6):36-41.
ZHANG Shuying,HU Youbiao,XING Shiping.Discrimination of the mine water inrush source based on principal component analyses-theory of gray relational degree[J].Hydrogeology and Engineering Geology,2018,45(6):36-41.