0 引言
振动慢剪破碎机是一种利用剪切挤压破碎原理和振动冲击破碎原理的高效破碎设备[1]。破碎机碎矿过程是一个多变量、强耦合、大时滞的复杂动态过程,过量给料会使矿料堵在破碎腔内产生堵塞现象,断料则会降低破碎机工作效率,同时振动电动机频率的波动会影响矿料粉碎程度。
近年来,许多学者针对破碎机控制开展了研究。杨丽荣[2]通过分析单缸液压圆锥破碎机运行状态,采用模糊控制器实现恒功率下给料量自动控制,动静态特性和抗干扰性能均优于传统的人工控制,具有较好的鲁棒性,但模糊控制参数选择具有较大主观随意性,导致控制性能无法达到最优。吴宇平等[3]提出了一种基于模糊遗传优化算法的破碎系统给矿量优化控制策略,利用遗传算法在线寻优能力动态调整模糊PID控制器参数,但易陷入局部最优。李爱莲等[4]针对液压圆锥破碎机碎矿过程中时变、非线性及大滞后等特性,采用模糊参数自整定PID控制和改进模糊Smith预估器补偿控制相结合的方法,克服了非线性、时滞及数学模型不匹配对破碎机控制的影响,但对反馈环节大纯滞后的补偿过程过于复杂,通用性不强。本文提出了一种振动慢剪破碎机模糊解耦PID控制方法,通过采用对角矩阵解耦与模糊PID控制相结合的方式,对给料量和振动电动机频率进行控制,并引入自适应粒子群优化(Adaptive Particle Swarm Optimization,APSO)算法对模糊PID控制参数进行优化,从而保证主电动机工作电流及合格矿料产率控制精度、稳定性和动态性能,实现振动慢剪破碎机的高效稳定运行。
1 振动慢剪破碎机动态模型
影响破碎机产能的主要参数包括振动电动机频率、给料量、主电动机工作电流和合格矿料产率[5]。设置给料量、振动电动机频率为输入量,主电动机工作电流、合格矿料产率为输出量,得到振动慢剪破碎机动态模型为
(1)
式中:I为主电动机工作电流;D为合格矿料产率;M为给料量;F为振动电动机频率;G11(s)为M对I的传递函数;G12(s)为F对I的传递函数;G21(s)为M对D的传递函数;G22(s)为F对D的传递函数;s为拉普拉斯算子。
本文通过破碎试验获取主电动机工作电流和合格矿料产率阶跃响应数据,并运用辨识拟合法[6]可得
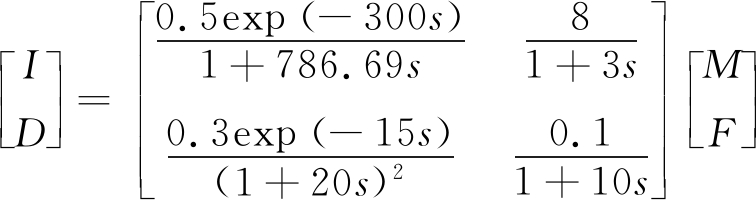
(2)
由式(2)可知,破碎过程中输入量与输出量表现为多变量之间的非线性关系,若采用多输入多输出系统进行模糊PID控制器设计,模糊控制规则较多,控制器设计较为复杂。
2 振动慢剪破碎机模糊解耦PID控制
振动慢剪破碎机模糊解耦PID控制原理如图1所示,其中Q11(s),Q12(s),Q21(s),Q22(s)分别为G22(s),G12(s),G21(s),G11(s)的解耦补偿传递函数。采用对角矩阵解耦与模糊PID控制相结合的方式来实现振动慢剪破碎机碎矿过程解耦控制,并加入反馈调节环节对模糊PID控制器进行调整。
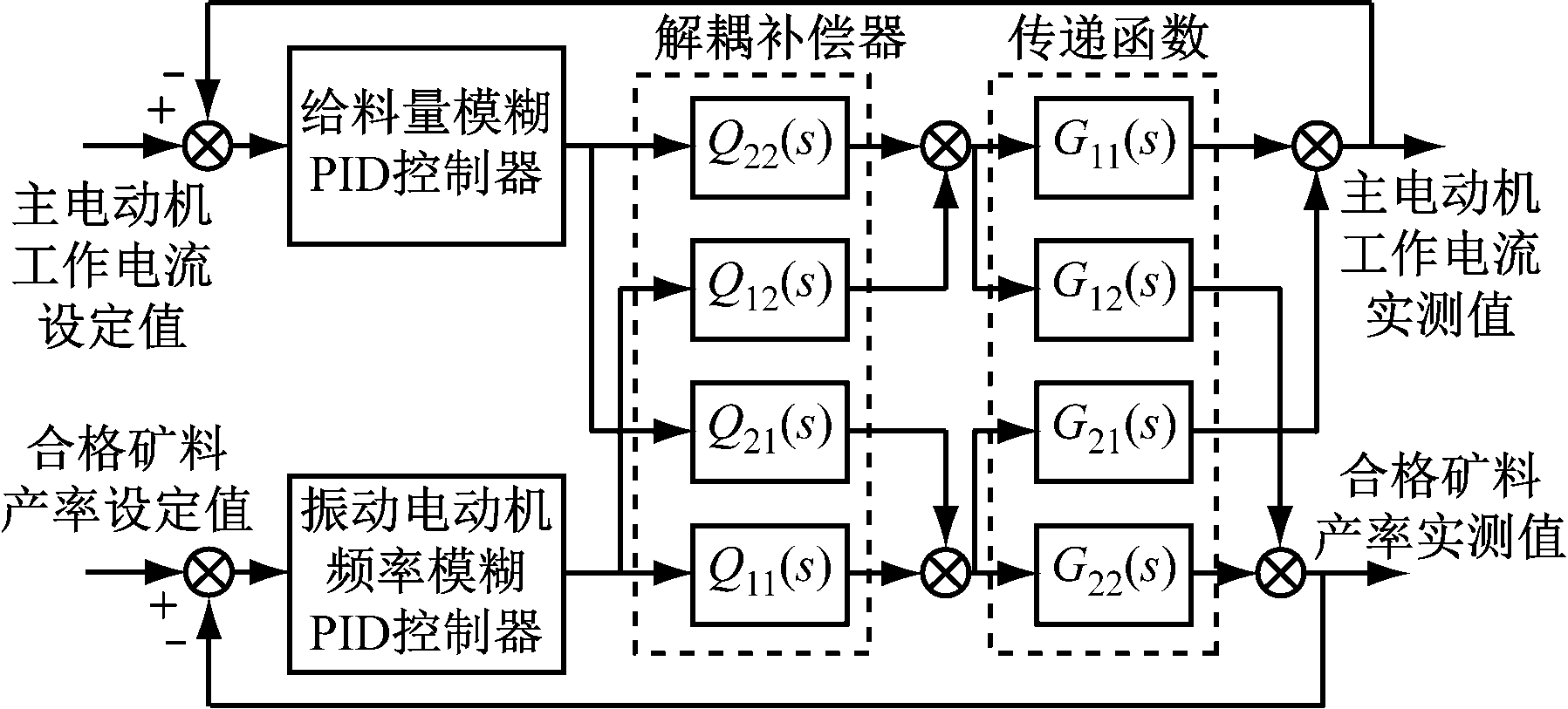
图1 振动慢剪破碎机模糊解耦PID控制原理
Fig.1 Principle of fuzzy decoupling PID control for vibration-slow shear crusher
2.1 对角矩阵解耦
对振动慢剪破碎机动态模型进行对角矩阵解耦:
![]()
![]()
(3)
式中![]() 为解耦后的传递函数矩阵。
为解耦后的传递函数矩阵。
经正交化处理可得
(4)
(5)
令
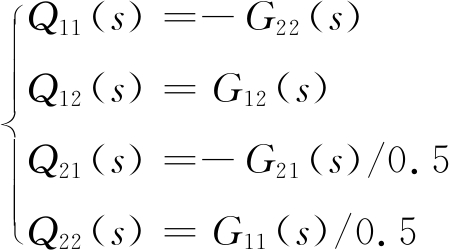
(6)
联立式(4)—式(6)可得
![]() Q11(s)G11(s)+Q12(s)G21(s)=
Q11(s)G11(s)+Q12(s)G21(s)=
(7)
![]() Q21(s)G12(s)+Q22(s)G22(s)=
Q21(s)G12(s)+Q22(s)G22(s)=
(8)
因此,经对角矩阵解耦后的振动慢剪破碎机动态模型为
![]()
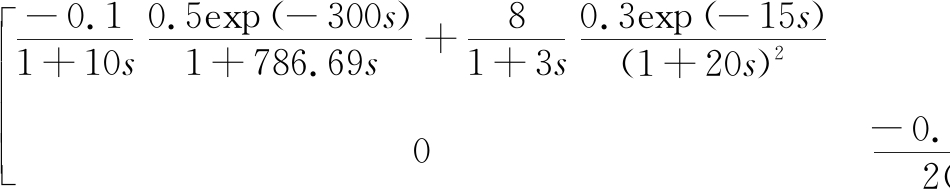
(9)
振动慢剪破碎机动态模型通过对角矩阵解耦分解为2个单输入单输出模型,即![]() 和
和![]() 因此设计2个相互独立的模糊PID控制器——给料量模糊PID控制器和振动电动机频率模糊PID控制器。
因此设计2个相互独立的模糊PID控制器——给料量模糊PID控制器和振动电动机频率模糊PID控制器。
2.2 模糊PID控制器
振动慢剪破碎机模糊解耦PID控制结构如图2所示。将主电动机工作电流和合格矿料产率的设定值与实测值比较,得到偏差及偏差变化率作为模糊PID控制器输入量,输入量经模糊化、模糊推理、参数修正后,得到PID控制器参数的增量,从而完成PID控制器参数调整,最终得到精确的模糊PID控制器输出量。
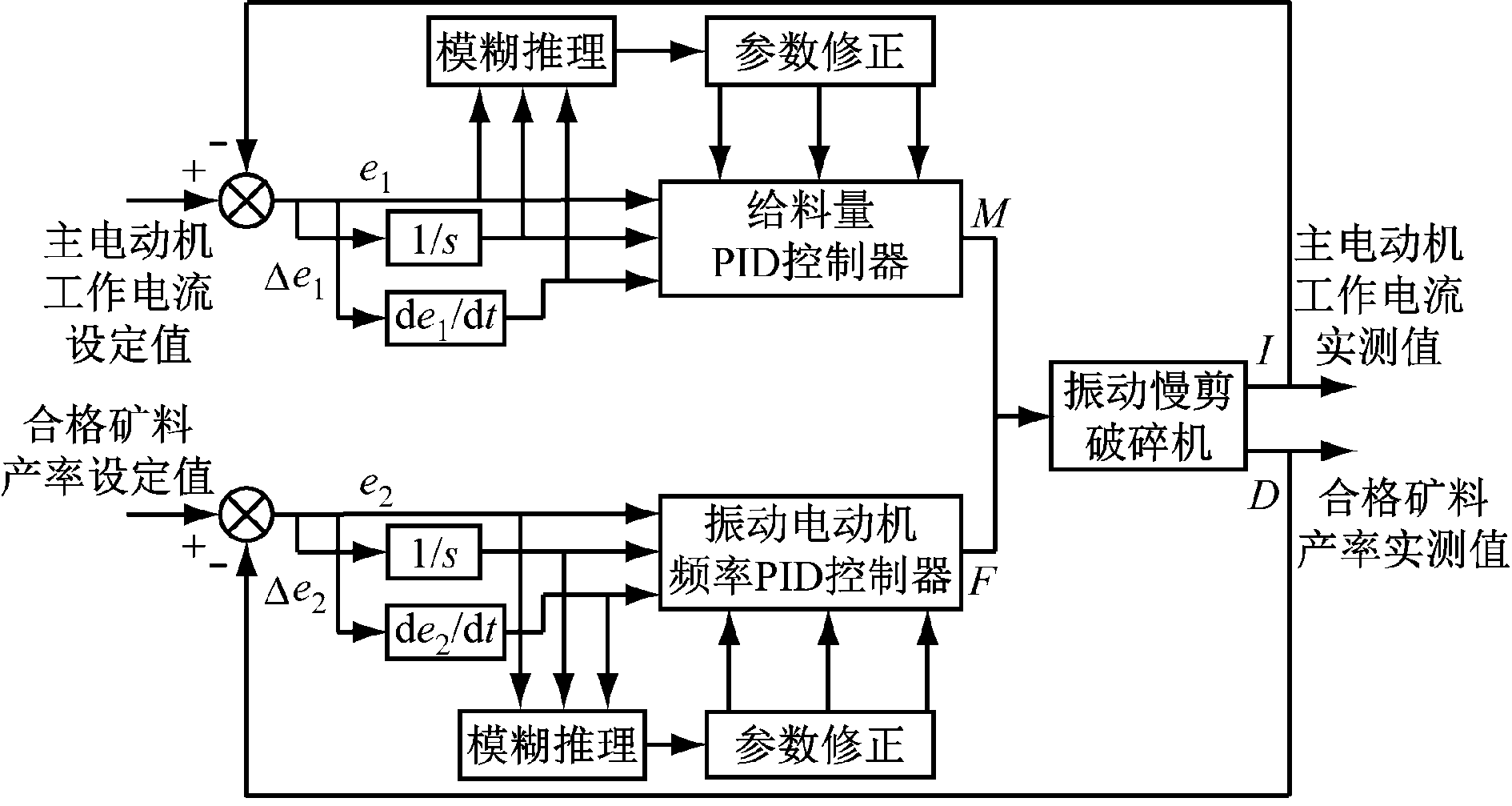
图2 振动慢剪破碎机模糊PID控制原理
Fig.2 Principle of fuzzy PID control for vibration-slow shear crusher
2.2.1 给料量模糊PID控制器
给料量模糊PID控制器采用双输入单输出结构进行设计,其中双输入为主电动机工作电流偏差e1及偏差变化率Δe1,单输出为给料量M。假设主电动机工作电流设定值、实测值分别为Q0,Q,则
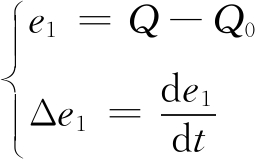
(10)
对输入量进行模糊化处理。通过分析现场试验数据进行设定:电流偏差e1的取值范围为[-40,40];电流偏差变化率Δe1的取值范围为[-10,10];给料量M的取值范围为[-12,12]。选取输入量和输出量的语言变量均为{NB,NS,Z,PS,PB},即{负大,负小,零,正小,正大},输入量和输出量的量化论域均可表示为{-2,-1,0,1,2}。在实际控制系统中,输入量的实际取值并非论域中元素,需要引入量化因子进行论域变换[7]。
由于每个输入量的模糊分级有5级,所以模糊PID控制器的模糊控制规则数为25条。设主电动机工作电流偏差、偏差变化率和给料量的模糊子集分别为Ai,Bi,Ci(i=1,2,…,5),采用模糊条件推理语句“ife1=Aiand Δe1=BithenCi”,得出模糊关系:
(11)
式中×为模糊子集之间的直积运算符。
依据模糊控制原理,得到给料量的模糊子集:
Ci=(Ai×Bi)∘R1
(12)
式中∘为模糊推理Mamdani(模糊蕴涵最小法)合成运算符。
采用最大平均隶属度法求输出量的语言变量,可得给料量模糊PID控制器模糊控制规则,见表1。
表1 给料量模糊PID控制器模糊控制规则
Table 1 Fuzzy control rules of fuzzy PID controller for ore feeding quantity

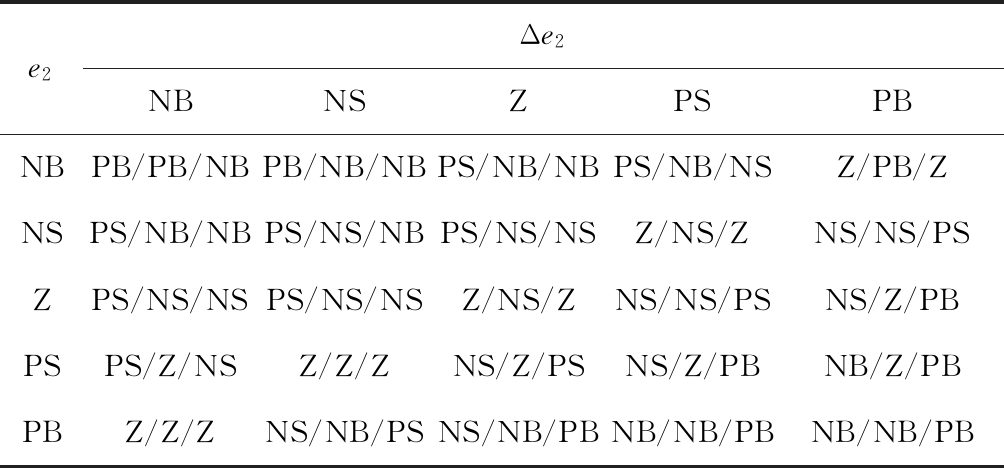
2.2.2 振动电动机频率模糊PID控制器
振动电动机频率模糊PID控制器设计原理与给料量模糊PID控制器一致。以合格矿料产率偏差e2及偏差变化率Δe2作为输入量,振动电动机频率F作为输出量。综合现场试验经验进行设置:输入量e2,Δe2的取值范围均为[-10,10];输出量F的取值范围为[-12,12]。选取输入量和输出量的语言变量值均为{NB,NS,Z,PS,PB},输入量和输出量的量化论域均为{-2,-1,0,1,2}。
由模糊推理得到振动电动机频率模糊PID控制器模糊控制规则,见表2。
3 基于APSO算法优化的模糊PID控制器
粒子群优化算法(Particle Swarm Optimization,PSO)是一种智能全局寻优算法,其基本思想是通过处于群体中的粒子信息共享、相互竞争,不断迭代最终寻得最优解[8-11]。考虑到传统PSO算法难以快速、精确地寻得最优解,采用APSO算法动态自适应调整惯性权重ω:
表2 振动电动机频率模糊PID控制器模糊控制规则
Table 2 Fuzzy control rules of fuzzy PID controller for vibration motor frequency

(13)
式中:ωmin,ωmax分别为惯性权重的最小值、最大值;f为当前粒子的适应度值;fmin,fave分别为粒子群适应度值的最小值、平均值。
由式(13)可知,当f≤fave时,粒子在当前最优解毗邻区域内做局部细致寻优;当f>fave时,当前粒子会增加搜索半径且以一个较大的步长搜索最优解,以保证粒子群解的多样性和良好的收敛性,跳出局部最优解。
隶属函数是影响模糊PID控制器性能的因素之一,其形状决定控制性能:凸峰明显即形状较陡时,控制灵敏度高;凸峰不明显即形状较平时,控制稳定性好[12-13]。隶属函数表达式为
fnm(xm)=

(14)
式中:xm为输入量;![]() 分别为第n(n=1,2,…,25)个模糊控制规则中第m(m=1,2)个输入量的隶属函数的中心、左宽、右宽。
分别为第n(n=1,2,…,25)个模糊控制规则中第m(m=1,2)个输入量的隶属函数的中心、左宽、右宽。
为使振动慢剪破碎机模糊PID控制性能达到最优,需要对模糊PID控制器的隶属函数形状参数进行动态优化。本文采用APSO算法,将模糊PID控制器输入量、输出量的隶属函数(采用全交叠、均匀分布的三角形隶属函数[14-15])中心点作为粒子群的粒子并根据当前控制器响应进行寻优。流程如图3所示,具体步骤如下。
(1) 初始化粒子群,并定义粒子的空间位置及飞行速度。

图3 APSO算法流程
Fig.3 APSO algorithm flow
(2) 根据目标函数计算当前粒子位置的适应度值f,根据适应度值来评价粒子位置的优劣,以确定当前粒子的局部最优位置及粒子种群最优位置。
(3) 将当前粒子位置的适应度值f与该粒子局部最优位置适应度值fpbest及粒子种群最优位置适应度值fgbest进行比较:若f>fpbest,则fpbest=f;若f>fgbest,则fgbest=f。
(4) 根据式(13)计算粒子惯性权重。
(5) 实时更新粒子的空间位置及飞行速度。
(6) 返回步骤(2)进行迭代,直到满足迭代次数要求,得到粒子种群最优位置。
4 仿真验证
利用Matlab/Simulink构建模糊解耦PID控制仿真模型,如图4所示。将基于APSO算法优化的模糊PID控制算法编写成m文件,并通过S函数模块导入仿真模型中;子系统模块内为经对角矩阵解耦后的振动慢剪破碎机动态模型。
为验证基于APSO算法优化的模糊PID控制的有效性,与传统模糊PID控制及基于遗传算法优化的模糊PID控制进行仿真对比。设置仿真时间为100 s,步长为0.01 s,得到3种算法下主电动机工作电流和合格矿料产率响应曲线,如图5所示。
由图5可知,与传统模糊PID控制和基于遗传算法优化的模糊PID控制相比,基于APSO算法优化的模糊PID控制响应速度更快、调节时间更短、最大超调量更小,实现了振动慢剪破碎机主电动机工作电流及合格矿料产率的稳定、高精度控制。

图4 模糊解耦PID控制仿真模型
Fig.4 Simulation model of fuzzy decoupling PID control
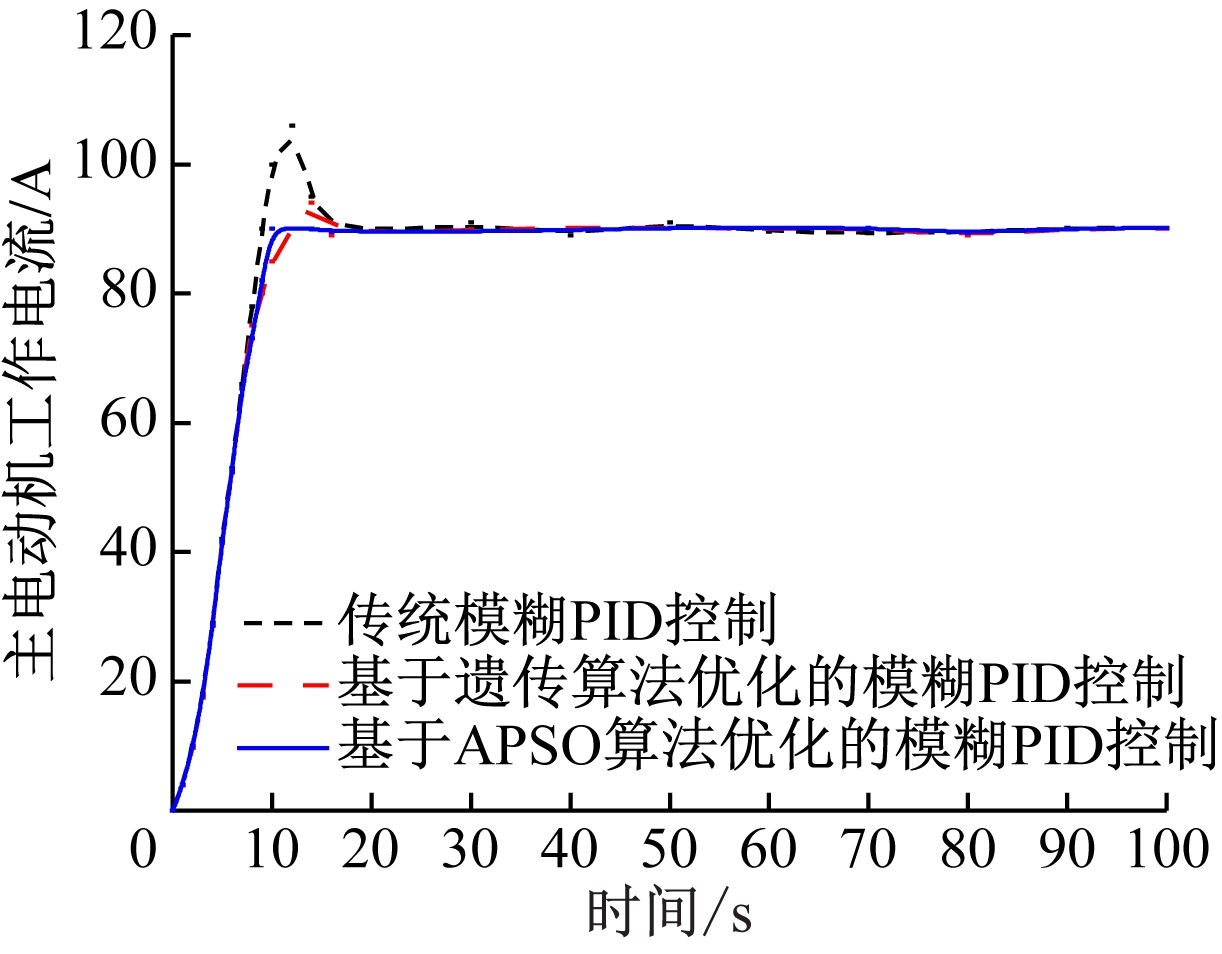
(a) 主电动机工作电流响应曲线

(b) 合格矿料产率响应曲线
图5 仿真结果
Fig.5 Simulation results
5 试验验证
为验证基于APSO算法优化的模糊PID控制器在振动慢剪破碎机控制中的可行性,搭建振动慢剪破碎机控制系统试验平台,总体结构如图6所示。以PLC作为主控制器(EM235为扩展的输入/输出模块,EM232为扩展的输出模块,EM277为扩展的通信模块),通过Profibus现场总线与工控机进行通信;在LabVIEW监控界面中实现振动慢剪破碎机工作状态显示及输入/输出量控制;利用光纤电流传感器测定主电动机工作电流,称重式传感器监测给料量及矿料产量,加速度传感器采集振动电动机振动信号,通过快速傅里叶变换分析仪检测振动电动机主频率;采用2台变频器分别控制振动电动机及主电动机的转速。
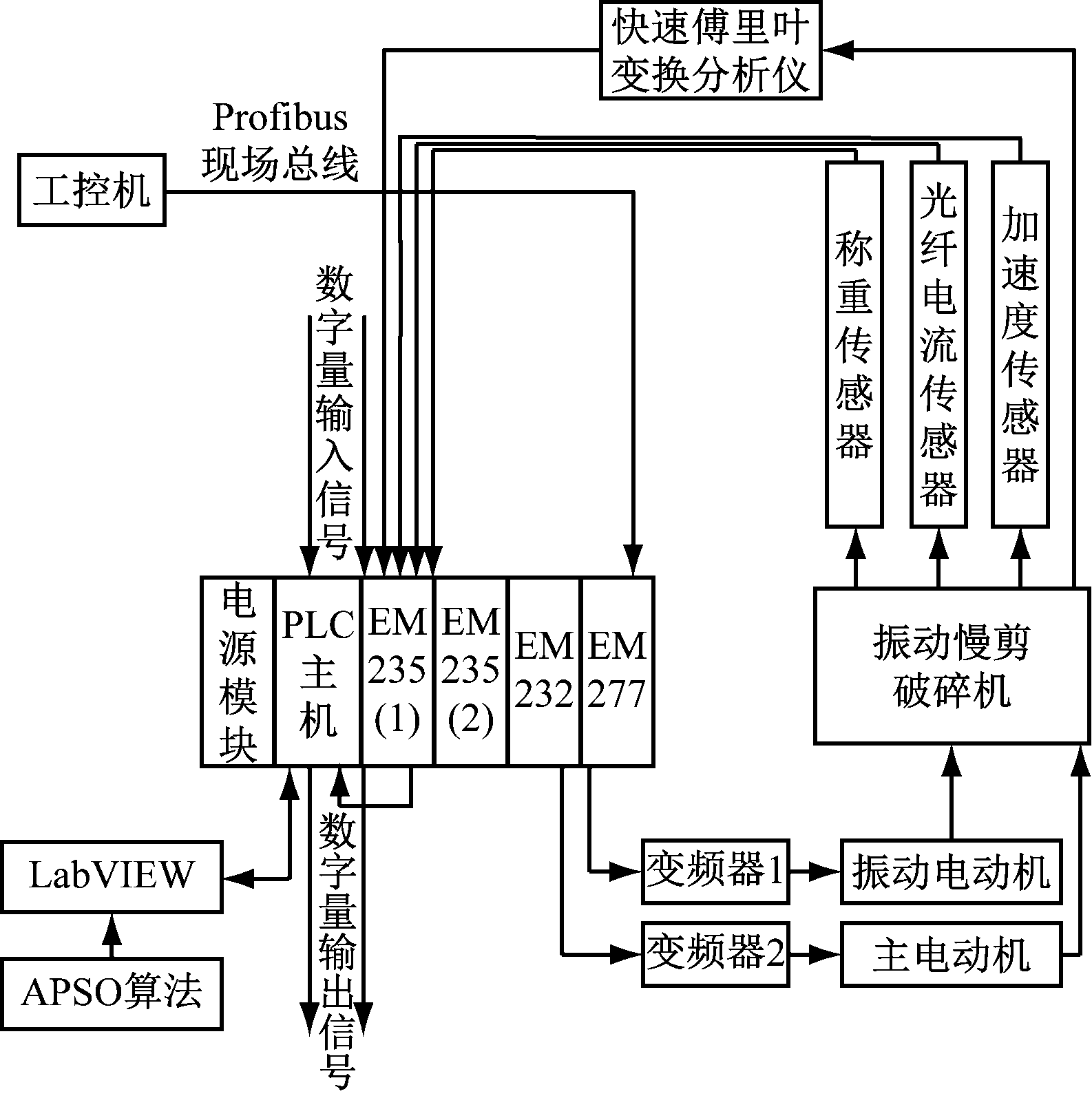
图6 振动慢剪破碎机控制系统总体结构
Fig.6 Overall structure of control system for vibration-
slow shear crusher
振动电动机为HB50-6型,双振幅为5.449 mm;主电动机为Y2VP225S-4型,其极对数为2,额定工作频率为50 Hz。为保证电动机使用寿命,转速取额定值的80%。主要试验参数见表3。
表3 试验参数
Table 3 Experimental parameters

试验结果如图7所示。可看出主电动机工作电流首次超调量约为10%,但能较快回归至设定值,50 s后达到稳定状态,且波动较小;合格矿料产率响应速度快、超调量小且调节时间短,50 s后合格矿料产率稳定在85%左右。
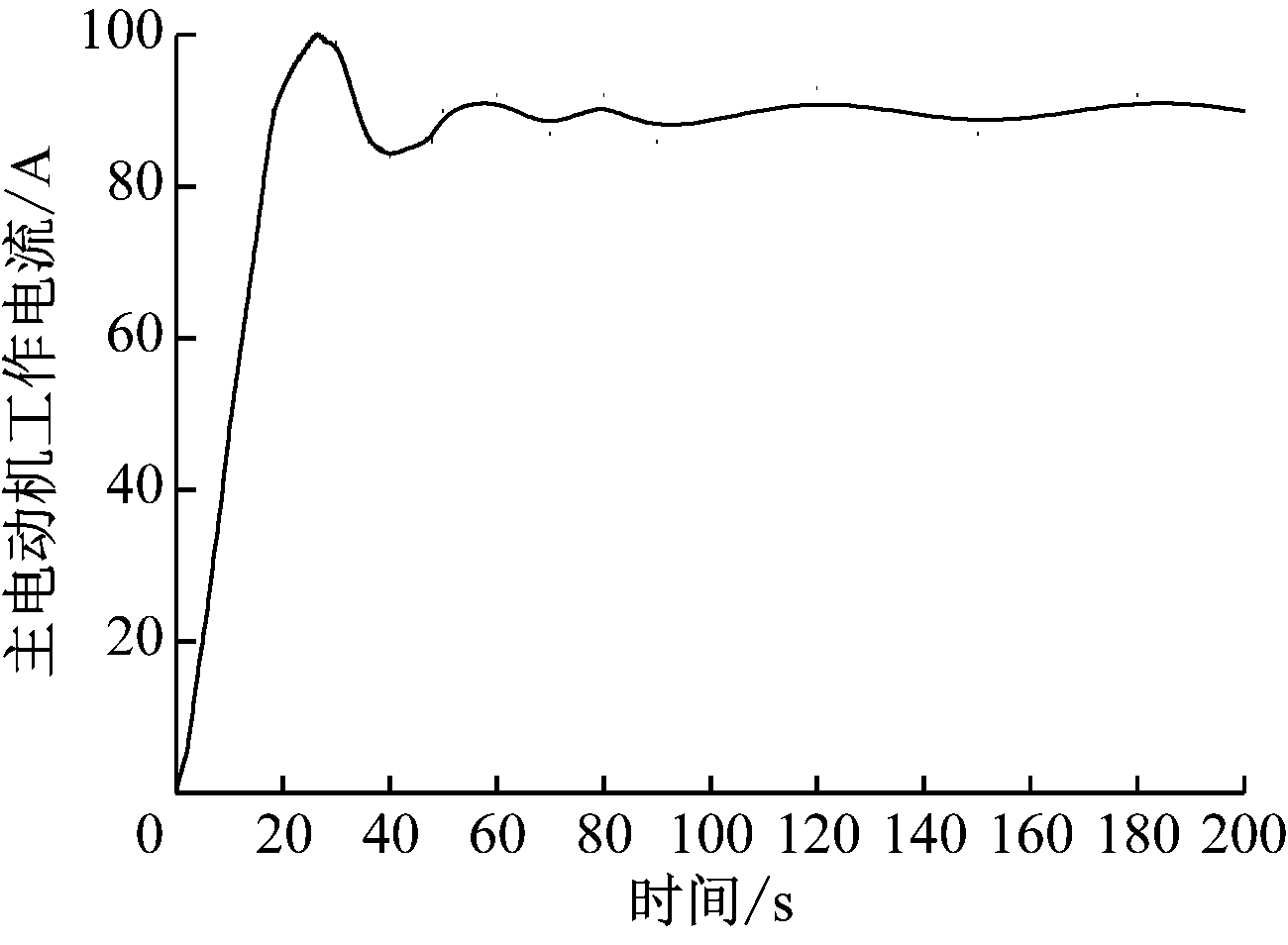
(a) 主电动机工作电流响应曲线

(b) 合格矿料产率响应曲线
图7 试验结果
Fig.7 Experimental results
6 结语
振动慢剪破碎机模糊解耦PID控制方法对多变量、强耦合的振动慢剪破碎机动态模型进行对角矩阵解耦,通过给料量模糊PID控制器和振动电动机频率模糊PID控制器对主电动机工作电流和合格矿料产率进行控制,并引入APSO算法对模糊PID控制器参数在线寻优。仿真与试验结果表明,该方法响应速度快、调节时间短、超调量小,实现了破碎过程中主电动机工作电流、合格矿料产率的稳定、有效控制。
参考文献(References):
[1] 李臣.振动慢剪破碎机破碎性能分析及实验研究[D].赣州:江西理工大学,2018.
LI Chen.Crushing performance analysis and experimental study on vibration-slow shear crusher[D].Ganzhou:Jiangxi University of Science and Technology,2018.
[2] 杨丽荣.基于PLC的单缸液压圆锥破碎机模糊控制系统的设计[J].工矿自动化,2009,35(10):117-118.
YANG Lirong.Design of fuzzy control system for single-cylinder hydraulic cone crusher based on PLC[J].Industry and Mine Automation,2009,35(10):117-118.
[3] 吴宇平,章家岩,吴其玲,等.基于模糊遗传算法的选矿破碎系统优化控制[J].微型电脑应用,2014,30(8):27-29.
WU Yuping,ZHANG Jiayan,WU Qiling,et al.Optimal control of the crushing system based on fuzzy genetic algorithm[J].Microcomputer Applications,2014,30(8):27-29.
[4] 李爱莲,岳峰.基于STM32的液压圆锥破碎机的智能控制[J].矿山机械,2012,40(8):68-73.
LI Ailian,YUE Feng.Intelligent control system for hydraulic crushers based on STM32[J].Mining & Processing Equipment,2012,40(8):68-73.
[5] 陈慧明.振动慢剪破碎机智能控制方法研究[D].赣州:江西理工大学,2018.
CHEN Huiming.Research on intelligent control method of vibration-slow shear crusher[D].Ganzhou:Jiangxi University of Science and Technology,2018.
[6] 罗国虎.预磨机破磨系统辨识与预测控制研究[D].赣州:江西理工大学,2013.
LUO Guohu.Research on identification and predictive control of grinding system of premill[D].Ganzhou:Jiangxi University of Science and Technology,2013.
[7] 王庆利,王丹,井元伟.基于模糊解耦的火电单元机组负荷控制[J].控制与决策,2006,21(4):435-439.
WANG Qingli,WANG Dan,JING Yuanwei.Load control based on fuzzy decoupling for fossil-fired electric single generating units[J].Control and Decision,2006,21(4):435-439.
[8] 韩睿松,杨维.基于改进粒子群优化的井下WMSN覆盖增强算法[J].中国矿业大学学报,2016,45(1):170-175.
HAN Ruisong,YANG Wei.A coverage-enhancing algorithm based on improved particle swarm optimization for WMSN of underground coal mine[J].Journal of China University of Mining & Technology,2016,45(1):170-175.
[9] 谢延敏,孙新强,田银,等.基于改进粒子群算法和小波神经网络的高强钢扭曲回弹工艺参数优化[J].机械工程学报,2016,52(19):162-167.
XIE Yanmin,SUN Xinqiang,TIAN Yin,et al.Optimization of parameters in twist springback process for high-strength sheets based on improved particle swarm optimization algorithm and wavelet neural network[J].Journal of Mechanical Engineering,2016,52(19):162-167.
[10] 叶满园,黄凯峰.基于改进粒子群算法的阶梯波调制功率均衡控制策略[J].工矿自动化,2015,41(9):57-62.
YE Manyuan,HUANG Kaifeng.Power balance control strategy for staircase modulation based on improved particle swarm optimization algorithm[J].Industry and Mine Automation,2015,41(9):57-62.
[11] 仝秋娟,赵岂,李萌.基于自适应动态改变的粒子群优化算法[J].微电子学与计算机,2019,36(2):6-10.
TONG Qiujuan,ZHAO Qi,LI Meng.Particle swarm optimization algorithm based on adaptive dynamic change[J].Microelectronics and Computer,2019,36(2):6-10.
[12] 唐少先,陈建二,张泰山.Mamdani模糊系统I/O关系的表示及隶属函数优化[J].控制理论与应用,2005,22(4):520-526.
TANG Shaoxian,CHEN Jianer,ZHANG Taishan.Mamdani fuzzy system I/O relation representative and membership function optimization[J].Control Theory & Applications,2005,22(4):520-526.
[13] 谢朝杰,保宏,杜敬利,等.一种新隶属度函数在非线性变增益模糊PID控制中的应用[J].信息与控制,2014,43(3):264-269.
XIE Chaojie,BAO Hong,DU Jingli,et al.Application of a new membership function to nonlinear fuzzy PID controllers with variable gains[J].Information and Control,2014,43(3):264-269.
[14] 王宁,孟宪尧.输入采用广义梯形隶属函数的两维最简模糊控制器结构分析[J].自动化学报,2008,34(4):466-471.
WANG Ning,MENG Xianyao.Structure analysis of two-dimensional simplest fuzzy controllers using generalized trapezoid-shaped input membership function[J].Acta Automatica Sinica,2008,34(4):466-471.
[15] 黄卫华,方康玲,章政.典型模糊控制器的隶属函数设计及分析[J].模糊系统与数学,2010,24(5):83-90.
HUANG Weihua,FANG Kangling,ZHANG Zheng.Analysis and design of membership function for a typical fuzzy controller[J].Fuzzy Systems and Mathematics,2010,24(5):83-90.