0 引言
随着煤层开采深度的增加，深部煤岩体大变形问题日益突出[1]。煤岩体的大变形不是瞬时发生的，而是长时间缓慢流变的结果，其中蠕变是煤岩体流变的主要表现形式[2]。煤体蠕变引起煤体渗透率改变，而煤体渗透率的变化对井下瓦斯抽采具有重要影响[3]。
煤体渗透率是表征煤体瓦斯运移难易程度的重要参数，渗透率的变化是煤体有效应力及煤基质收缩与膨胀变形所导致的[4-5]。国内外相关学者对煤体渗透率模型及蠕变对煤体渗流的影响进行了大量研究。李志强等[6]开展了不同应力和不同温度煤体渗流实验，发现不同有效应力下，煤体渗透率与温度的关系并非单调递增或递减，而是存在转折区。TAN Yuling等[7]通过取同块煤的不同煤样，在不同气压和围压下进行了煤体渗透率实验，利用X-ray技术分析了煤样的宏观裂隙分布，结合实验与数值模拟结果得知煤体渗透率具有很强的各向异性和非均质特性。ZHANG Hongbin等[8]认为煤体的吸附膨胀对煤体渗透率有重要影响，建立了考虑吸附膨胀变形与有效应力的煤体渗透率模型，并与PM模型进行了对比分析。ZHU Jianfang等[9]认为煤体蠕变是煤矿开采中不可避免的，煤体蠕变与气体流动相互作用和影响，开展了蠕变渗流实验并分析了蠕变渗流的演化规律。N.Danesh等[10]建立了蠕变渗流模型，并开展了蠕变渗流实验及瓦斯抽采过程中蠕变渗流演化规律数值模拟研究，分析了不同条件下蠕变对煤体渗透率的影响。
基于上述研究发现，目前对于煤层瓦斯渗流的研究大多基于煤体的弹性变形，考虑蠕变及钻孔卸压综合作用下瓦斯渗流及抽采钻孔布置的研究较少。本文基于煤体的双重孔隙介质特征，建立了考虑蠕变作用的煤体变形场、瓦斯扩散场及瓦斯渗流场多场耦合的数学模型，模拟分析了煤层瓦斯抽采动态变化规律，通过现场测试结果对数学模型进行了验证，并根据数值模拟结果得出了煤体瓦斯渗流规律及确定了瓦斯抽采钻孔最合理间距。
1 煤体蠕变作用下瓦斯渗流多场耦合数学模型
为了更好地分析煤层瓦斯流动演化规律，在以下假设基础上建立数学模型[4-5]：① 煤体是双重孔隙介质线弹性模型，其变形属于小变形。② 煤体是均质、各向同性的。③ 煤体是等温的，不考虑温度对瓦斯吸附解吸的影响。④ 煤体蠕变变形为黏弹性变形，变形过程中泊松比不发生变化。⑤ 煤层中瓦斯为理想气体，其在裂隙中的流动服从达西定律，在煤基质中的扩散服从菲克定律。
1.1 煤体蠕变模型
煤体蠕变一般分为3个阶段，如图1所示。第 Ⅰ 阶段为减速蠕变阶段，煤体蠕变变形速率逐渐变缓；第 Ⅱ 阶段为稳定蠕变阶段，蠕变变形速率基本为0；第 Ⅲ 阶段为加速蠕变阶段，煤体蠕变变形速率迅速增大直至煤体塑性破坏[11]。
图1 煤体蠕变曲线
Fig.1 Coal body creep curve
本文基于前人相关研究[12-13]，发现Burges模型(式(1))能比较清晰、全面地反映煤体蠕变过程中的弹-黏弹性变形过程。Burges模型的几何原理如图2所示。
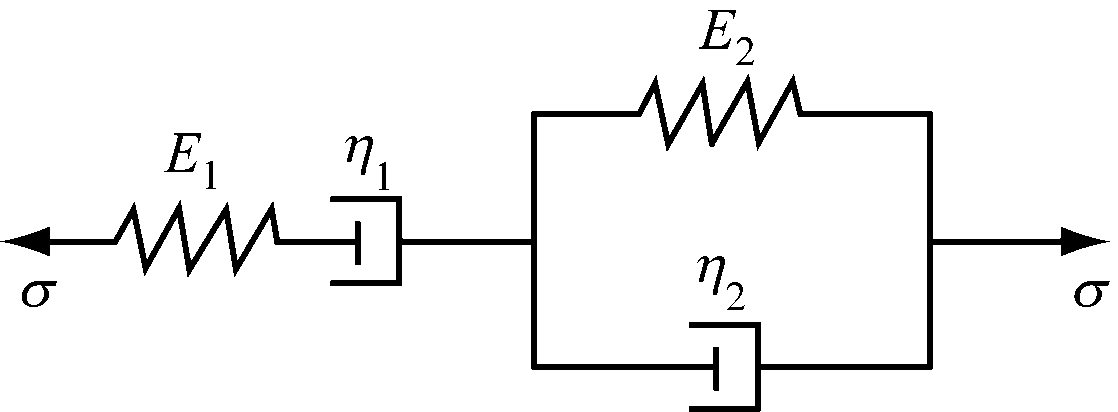
图2 Burges模型
Fig.2 Burges model
σ+
(1)
式中：σ为有效应力；η1，η2为蠕变黏性系数；E1为煤体弹性模量；E2为蠕变弹性系数；ε为煤体蠕变应变。
将式(1)转换为本构关系的一般形式：
P(A)σ=B(A)ε
(2)
式中：A为对时间t的微分算子，
对式(2)进行Laplace变换与逆变换，得到Burges模型的蠕变模量：
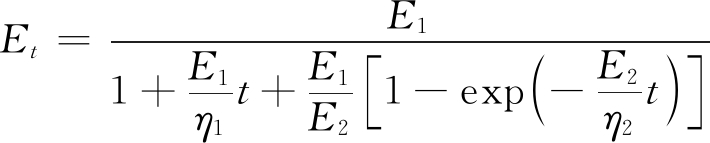
(3)
1.2 煤体变形控制方程
煤体被认为是一种线弹性多孔介质，煤体中包含基质和裂隙。进行瓦斯抽采时，煤体的力学平衡状态被破坏，煤体发生变形。煤体变形主要受2个方面因素的影响：① 瓦斯压力的降低导致煤体有效应力增加。② 瓦斯吸附与解吸导致煤基质膨胀与收缩变形。因此煤体变形方程可以表示为[14]
Gui,jj+
uj,ji-αmpm,i-αfpf,i-Kεs,i+fi=0
(4)
式中：G为煤体的剪切模量，
为泊松比；ui,uj分别为煤体在i,j(i,j=x,y,z)方向的位移；αm，αf为Biot's系数，
为煤体体积模量，
为煤基质体积模量，
为煤基质蠕变模量；Kf为裂隙体积模量；pm为煤基质瓦斯压力；pf为裂隙瓦斯压力；εs为煤体吸附膨胀或解吸收缩应变，
为Langmuir极限吸附变形量，pL为Langmuir压力常数；fi为煤体的体积力。
1.3 孔隙率和渗透率控制方程
煤基质孔隙率方程为[15]
φm=
(5)
式中：φm为煤基质孔隙率；φm0为初始煤基质孔隙率；Kp为煤基质孔隙体积模量；Lf为裂隙宽度；Lm为煤基质宽度；pm0为初始煤基质瓦斯压力；εV为煤层体积应变。
裂隙孔隙率方程为
(6)
式中：φf为裂隙孔隙率；φf0为初始裂隙孔隙率。
根据立方定律可知，裂隙渗透率方程为
(7)
式中：kf为裂隙渗透率；kf0为初始裂隙渗透率。
1.4 煤基质瓦斯扩散控制方程
煤层中瓦斯的扩散渗流过程符合质量守恒定律，煤基质与裂隙瓦斯质量交换控制方程为[15]
(8)
式中：Qs为质量源；MC为摩尔质量；D0为初始扩散系数；λ为扩散衰减系数；R为气体常数；T为温度。
单位体积煤基质瓦斯含量方程为
(9)
式中：mm为单位体积煤基质瓦斯含量；a为Langmuir体积常数；b为吸附平衡常数；ρ为煤体密度；Vm为气体摩尔体积。
由式(8)、式(9)可得煤体扩散场方程：
(10)
1.5 裂隙瓦斯渗流控制方程
根据质量守恒定律可知，单位体积的煤体裂隙内游离瓦斯含量随时间的变化量等于单位时间裂隙流出的瓦斯含量与煤基质扩散的瓦斯含量之和，从而可得裂隙瓦斯渗流控制方程：
×
(11)
式中μ为气体动态黏度。
2 煤层瓦斯抽采几何模型
本文以陕西彬长胡家河矿业有限公司煤层条件为依据，在COMSOL Multiphysics软件中建立了煤层单孔和双孔抽采模型，如图3所示。模型尺寸均为30 m×10 m，钻孔直径为113 mm，煤层初始瓦斯压力为0.5 MPa。顶部边界为上覆岩层应力(15 MPa)，左右边界为辊支撑，底部边界为固定约束。测点1—4分别距钻孔中心1，2，3，4 m。模型所用参数部分来自陕西彬长胡家河矿业有限公司实际监测，部分来自文献，见表1[14-15]。
(a) 单孔抽采模型
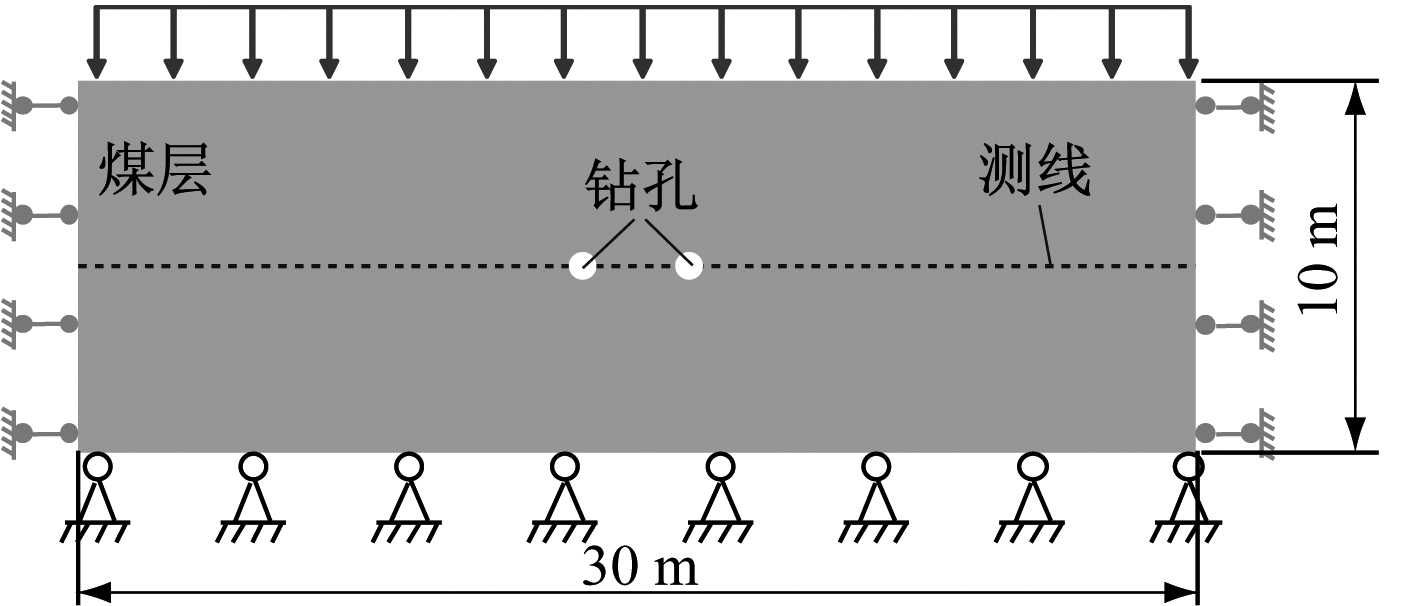
(b) 双孔抽采模型
图3 煤层瓦斯抽采几何模型
Fig.3 Geometric models of gas drainage in coal seam
表1 模型基本参数
Table 1 Basic parameters of model
3 数值模拟结果与分析
3.1 模型验证
采用数学模型和单孔抽采模型对煤层钻孔抽采瓦斯动态过程进行数值模拟研究，并将模拟结果与陕西彬长胡家河矿业有限公司现场监测所得的30 d内单孔瓦斯抽采流量进行对比，结果如图4所示。可看出数值模拟结果与现场监测结果具有很好的拟合性，即数值模拟结果与现场监测结果吻合，可用于预测现场煤层钻孔产气率变化趋势。这验证了所建数学模型的正确性、合理性、可靠性及工程适用性，为现场钻孔布置和施工提供了理论支撑。
图4 数值模拟结果与现场监测结果对比
Fig.4 Comparison between numerical simulation and field monitoring results
3.2 单孔抽采瓦斯压力与渗透率的空间演化规律
单孔抽采时不同抽采时间煤层瓦斯压力和渗透率变化云图如图5所示。
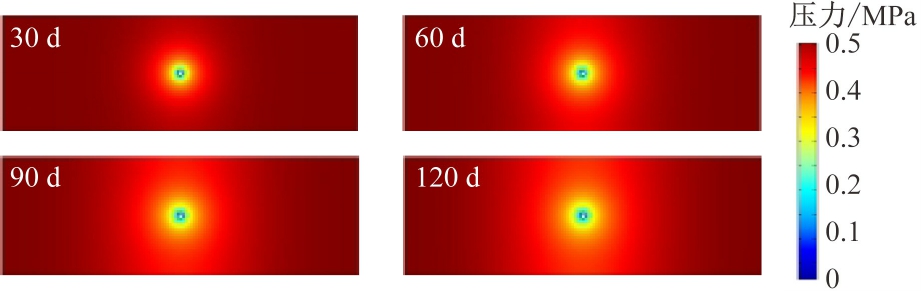
(a) 瓦斯压力
(b) 渗透率
图5 不同抽采时间瓦斯压力和渗透率变化云图
Fig.5 Variation nephogram of gas pressure and permeability at different drainage time
从图5(a)可看出，随着抽采时间延长，煤层钻孔周围瓦斯压力逐渐降低，钻孔抽采影响区域呈圆形向四周扩展。从图5(b)可看出，随着抽采时间延长，煤层渗透率逐渐增大，主要原因是在煤层瓦斯抽采过程中，煤层在应力作用下逐渐发生蠕变变形，且煤层瓦斯的解吸流动导致煤基质收缩，从而使煤层渗透率逐渐增大。
不同抽采时间瓦斯压力和渗透率的空间演化规律如图6所示。从图6(a)可看出：沿煤层测线方向，不同抽采时间下瓦斯压力均随距钻孔距离的增加而增大，且距钻孔越近，瓦斯压力梯度越大，瓦斯压力变化越大，在远离钻孔处瓦斯压力逐渐趋于稳定；随着抽采时间延长，钻孔周围瓦斯压力逐渐减小，主要原因是瓦斯抽采前期钻孔瓦斯抽采流量较大，并可在一段时间内持续稳定抽采，随着抽采时间延长，煤层瓦斯抽采流量逐步减少并趋于平缓。从图6(b)可看出：受钻孔周围煤体卸压作用的影响，距钻孔越近，煤体渗透率比值越大，距钻孔越远，煤体渗透率比值越小并趋于稳定；随着抽采时间延长，渗透率比值逐渐增大，其原因在于随着煤层瓦斯的抽采，在钻孔抽采负压影响下，钻孔附近瓦斯压力逐渐降低，钻孔受到卸压扰动及煤基质收缩影响，导致煤体渗透率逐渐增大，但随着抽采时间延长及有效应力增大，煤体逐渐发生蠕变变形，使得渗透率变化幅度变缓。
(a) 瓦斯压力
(b) 渗透率
图6 不同抽采时间瓦斯压力和渗透率的空间演化规律
Fig.6 Spatial evolution laws of gas pressure and permeability at different drainage time
3.3 单孔抽采瓦斯压力与渗透率的时间演化规律
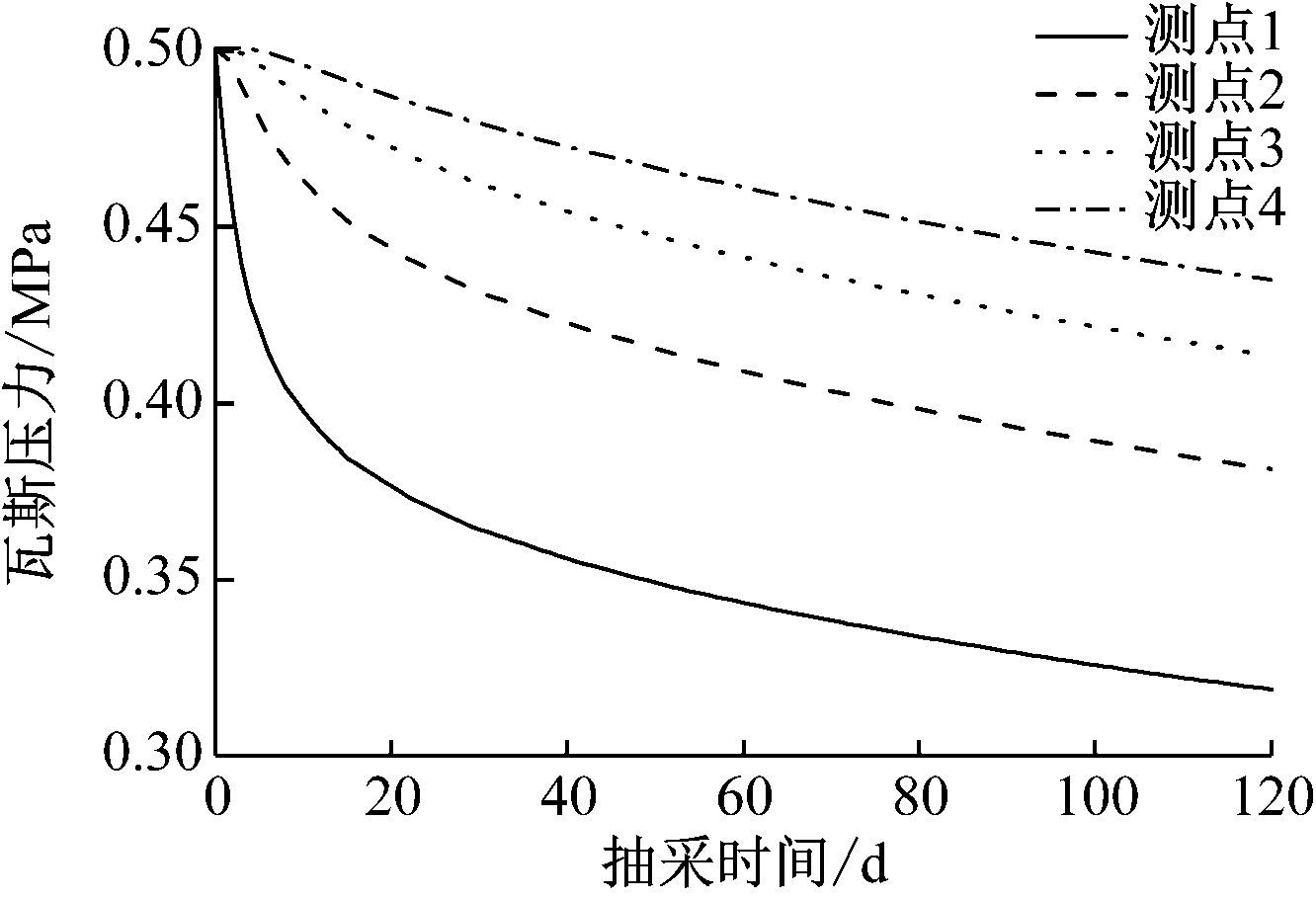
单孔抽采时距钻孔不同距离瓦斯压力和渗透率的时间演化规律如图7所示。从图7(a)可看出：距钻孔越近，在抽采初期瓦斯压力降低幅度越大，原因是距钻孔越近，在抽采初期所受的煤层压力梯度影响越大，导致瓦斯压力降低幅度较大，而距钻孔越远，抽采负压的影响越弱，瓦斯压力梯度越小；随着抽采时间延长，瓦斯压力降低幅度逐渐变缓，原因是随着抽采时间延长，压力梯度逐渐降低，导致瓦斯压力变化逐渐变缓。从图7(b)可看出：随着抽采时间的延长，不同测点处煤体渗透率比值逐渐增大，且距钻孔较近的测点煤体渗透率比值增加幅度较大，主要原因是距钻孔越近，瓦斯压力迅速降低对钻孔周围煤层的卸压效果越明显，进一步导致钻孔周围裂隙增大，渗透率比值呈迅速增大趋势；随着抽采时间的延长，渗透率比值增大的幅度逐渐变小，主要原因是在应力和瓦斯压力共同作用下，煤体逐渐发生蠕变变形，导致渗透率变化趋势变缓。
(a) 瓦斯压力
(b) 渗透率
图7 距钻孔不同距离瓦斯压力和渗透率的时间演化规律
Fig.7 Temporal evolution laws of gas pressure and permeability at different distances away form boreholes
3.4 双孔抽采钻孔合理间距
以单孔抽采数值模拟结果为基础，研究了双孔抽采瓦斯压力的演化规律，分析了钻孔合理布置间距。结合陕西彬长胡家河矿业有限公司煤层瓦斯赋存情况及地质条件，模拟了钻孔间距分别为1，2，3，4 m的情况，对比了不同抽采时间内瓦斯压力变化情况，如图8所示。
从图8可看出：随着抽采时间延长，钻孔周围瓦斯压力逐渐降低，且与单孔瓦斯抽采相比，两钻孔间相互耦合作用导致瓦斯压力降低幅度较大；钻孔间距越小，不同抽采时间内两钻孔间的瓦斯压力梯度均越小，说明钻孔间距越小，在相同抽采负压下，随着抽采时间延长，钻孔间瓦斯压力降低幅度越小，钻孔瓦斯抽采效率越低；抽采120 d后，钻孔间距为1，2，3，4 m时，两钻孔间最大瓦斯压力分别为0.120，0.200，0.245，0.280 MPa，瓦斯压力分别下降了76%，60%，51%，44%，可见随着抽采时间延长，钻孔间距为1 m时瓦斯抽采效果最好，其次是间距2，3 m，间距4 m时抽采效果较差。因陕西彬长胡家河矿业有限公司煤层原始瓦斯压力较低，考虑到瓦斯抽采钻孔施工的经济性，认为煤层瓦斯压力降低幅度达60%时即为实现了有效抽采。为保证煤层瓦斯抽采效率、优化钻孔数量、提高工程进度，确定瓦斯抽采钻孔最合理间距为2 m。
(a) 孔间距1 m
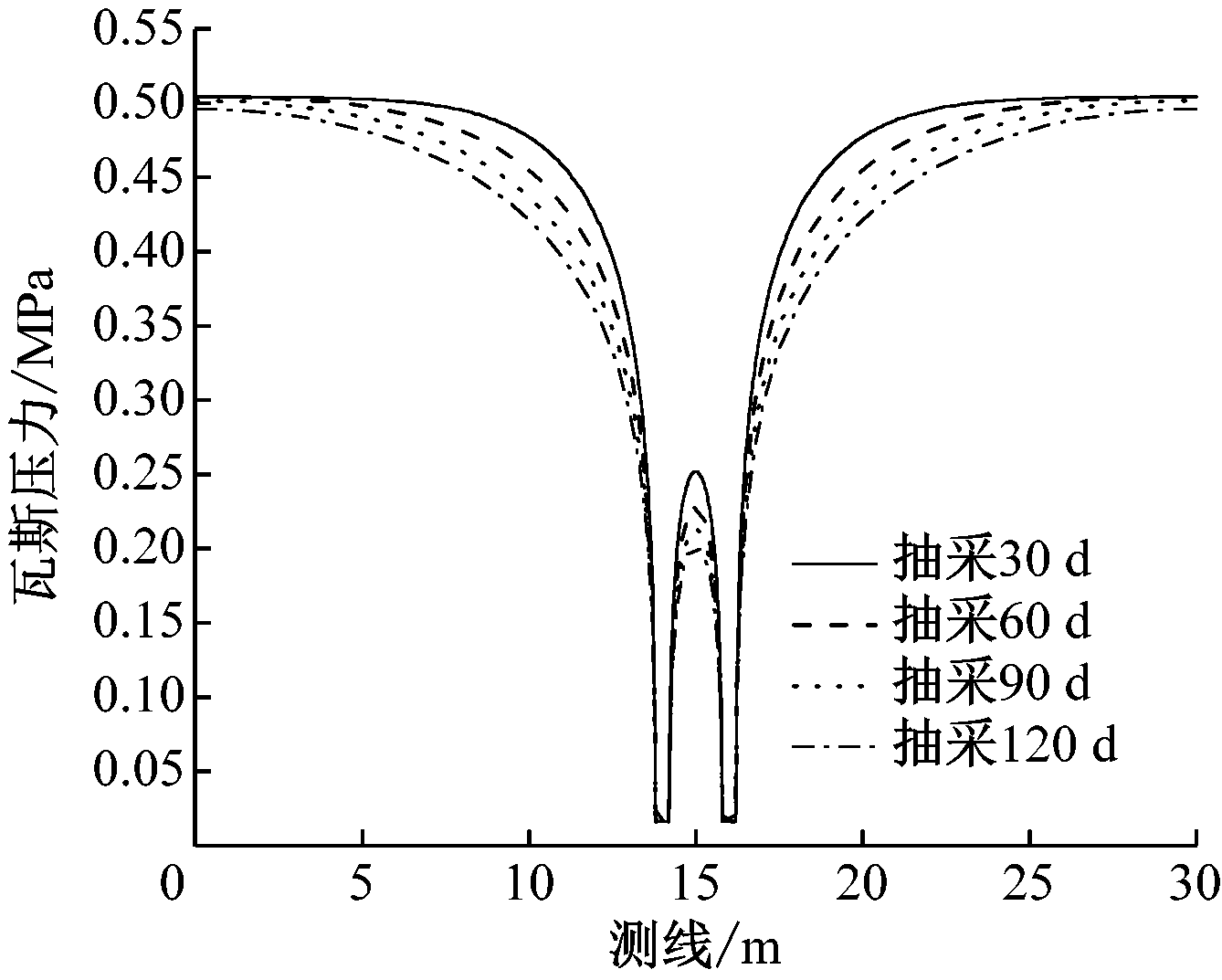
(b) 孔间距2 m
(c) 孔间距3 m
(d) 孔间距4 m
图8 不同抽采时间煤层瓦斯压力演化规律
Fig.8 Variation law of gas pressure in coal seam at different drainage time
4 结论
(1) 基于煤体的双重孔隙介质线弹性模型，建立了考虑蠕变作用的煤体变形场、瓦斯扩散场及瓦斯渗流场多场耦合的数学模型。以陕西彬长胡家河矿业有限公司瓦斯赋存及地质条件为依据，模拟分析了煤层瓦斯抽采动态变化规律，所得钻孔瓦斯抽采流量模拟结果与现场测试结果吻合，验证了所建数学模型的正确性、合理性、可靠性及工程适用性。
(2) 研究了单孔抽采瓦斯压力与渗透率的空间演化规律：煤层瓦斯压力随距抽采钻孔距离的增加而增大，距钻孔越近，瓦斯压力梯度越大，在远离钻孔处瓦斯压力逐渐趋于稳定；受煤体卸压扰动及煤基质收缩影响，距钻孔越近，煤体渗透率比值越大，距钻孔越远，煤体渗透率比值越小并趋于稳定。
(3) 研究了单孔抽采瓦斯压力与渗透率的时间演化规律：在瓦斯抽采初期，距钻孔越近煤体的瓦斯压力降低幅度越大，随着抽采时间延长，瓦斯压力降低的幅度逐渐变缓；在瓦斯抽采初期，距钻孔较近煤体的渗透率比值增加幅度较大，随着抽采时间的延长，在应力和瓦斯压力共同作用下，煤体的蠕变变形导致渗透率比值增加的趋势趋于平缓。
(4) 研究了双孔抽采瓦斯压力演化规律：与单孔瓦斯抽采相比，双孔抽采可显著降低煤层瓦斯压力；钻孔间距越小，不同抽采时间内两钻孔间的瓦斯压力梯度越小，但随着抽采时间延长，瓦斯抽采效率越低。结合陕西彬长胡家河矿业有限公司瓦斯赋存条件，确定其瓦斯抽采钻孔最合理间距为2 m。
参考文献（Ｒｅｆｅｒｅｎｃｅｓ）：
[1] LIU Zaobao,SHAO Jianfu,XIE Shouyi,et al.Effects of relative humidity and mineral compositions on creep deformation and failure of a claystone under compression[J].International Journal of Rock Mechanics and Mining Sciences,2018,103:68-76.
[2] WANG Dengke,WEI Jianping,YIN Guangzhi,et al.Triaxial creep behavior of coal containing gas in laboratory[J].Procedia Engineering,2011,26:1001-1010.
[3] 田坤云.应力加卸载作用下软硬原煤瓦斯渗透规律[J].西安科技大学学报,2017,37(6):790-794.
TIAN Kunyun.Gas seepage rule of soft and hard raw coal samples under the action of stress loading and unloading[J].Journal of Xi'an University of Science and Technology,2017,37(6):790-794.
[4] 林柏泉,赵洋,刘厅,等.水力割缝煤体多场耦合响应规律研究[J].西安科技大学学报,2017,37(5):662-667.
LIN Baiquan,ZHAO Yang,LIU Ting,et al.Coupling response law of multi-field in coal seam after hydraulic slotting[J].Journal of Xi'an University of Science and Technology,2017,37(5):662-667.
[5] 林柏泉,刘厅,杨威.基于动态扩散的煤层多场耦合模型建立及应用[J].中国矿业大学学报,2018,47(1):32-39.
LIN Baiquan,LIU Ting,YANG Wei.Solid-gas coupling model for coalseams based on dynamic diffusion and its application[J].Journal of China University of Mining & Technology,2018,47(1):32-39.
[6] 李志强,鲜学福,隆晴明.不同温度应力条件下煤体渗透率实验研究[J].中国矿业大学学报,2009,38(4):523-527.
LI Zhiqiang,XIAN Xuefu,LONG Qingming.Experiment study of coal permeability under different temperature and stress[J].Journal of China University of Mining & Technology,2009,38(4):523-527.
[7] TAN Yuling,PAN Zhejun,LIU Jishan,et al. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part II: permeability[J].Fuel， 2018,230:397-409.
[8] ZHANG Hongbin,LIU Jishan,ELSWORTH D. How sorption-induced matrix deformation affects gas flow in coal seams: a new FE model [J].International Journal of Rock Mechanics & Mining Sciences,2008,45(8):1226-1236.
[9] ZHU Jianfang,YANG Xiaobin,HE Ning.Experimental research on coal rock creep deformation-seepage coupling law[J].Procedia Engineering,2001,26:1526-1531.
[10] DANESH N,CHEN Zhongwei,AMINOSSADATI S,et al.Impact of creep on the evolution of coal permeability and gas drainage performance[J].Journal of Natural Gas Science and Engineering,2016,33:469-482.
[11] 陈占清，李顺才，浦海，等.采动岩体蠕变与渗流耦合动力学[M].北京:科学出版社,2010.
CHEN Zhanqing,LI Shuncai,PU Hai,et al.Creep and seepage coupling dynamics of mining rock mass[M].Beijing:Science Press,2010.
[12] 浦海,曹丽丽,邱艳勇,等.充填开采中渗流对覆岩蠕变影响规律的研究[J].采矿与安全工程学报,2015,32(5):846-852.
PU Hai,CAO Lili,QIU Yanyong,et al.Study of overlying strata creep affected by seepage in backfilling mining process[J].Journal of Mining & Safety Engineering,2015,32(5):846-852.
[13] 魏佳,王永岩,齐珺,等.蠕变作用下多孔介质渗流的固流耦合数学模型[J].辽宁工程技术大学学报(自然科学版),2011,30(5):726-729.
WEI Jia,WANG Yongyan,QI Jun,et al.Mathematical model of seepage in porous medium on account of solid-fluid coupling and creep effect[J].Journal of Liaoning Technical University(Natural Science),2011,30(5):726-729.
[14] ZHAO Yang, LIN Baiquan, LIU Ting, et al.Flow field evolution during gas depletion considering creep deformation[J]. Journal of Natural Gas Science and Engineering,2019,65:45-55.
[15] LIU Ting,LIU Tong.Coal permeability evolution and gas migration under non-equilibrium state[J].Transport in Porous Media,2017,118(3):393-416.