0 引言
当煤矿井下发生灾害时，精确的人员定位可以让救援团队迅速、准确地确定受困人员位置，大大提高救援效率，保障作业人员的生命安全。随着国家对煤矿安全生产日益重视，建立智能化、现代化的人员管理系统是一大趋势[1-2]。无线传感器网络(Wireless Sensor Network, WSN)是确保煤矿生产和煤矿信息化安全的重要手段，基于WSN的煤矿井下人员精确定位已成为安全生产的核心问题[3]。
WSN定位算法大致分为基于非测距的定位算法和基于测距的定位算法[4-5]。基于非测距的定位算法是根据节点之间的跳数以及网络的连通度进行定位，质心算法、Amorphous算法、DV-Hop算法等都属于非测距定位算法，这类算法计算简单，成本低，但定位精度不高[6]。在基于测距的定位算法中，常用的方法有信号到达时间(Time of Arrival，TOA)、信号到达时间差(Time Difference of Arrival，TDOA)、信号到达角度(Angle of Arrival，AOA)以及接收信号强度(Received Signal Strength Indicator，RSSI)等，该类算法利用测距技术，根据节点之间的距离确定目标的位置，定位精度较高，能够满足大部分场景的应用[7-8]。相比于TOA、TDOA、AOA等，RSSI成本更低，获取信号更加容易，在煤矿井下定位中最为常用。但由于井下环境复杂多变，非视距、温湿度等因素均会影响RSSI信号的传播，使得定位结果出现较大偏差。为了减小井下定位误差，研究人员对RSSI井下定位方法进行了改进。文献[9]采用加权二乘拟合的方式计算环境参量并构建特定的RSSI信号传输模型，根据最小均方差迭代算法计算未知节点坐标。文献[10]建立了信号衰减模型，动态获取无线信号的路径衰落指数，以提高测距精度，并通过改进的加权质心算法计算未知节点坐标。文献[11]利用链路质量指示(Link Quality Indicator，LQI)指标处理RSSI测量数据，并使用联合估计方法计算环境参数以优化测量距离，再根据最小二乘法进行节点定位。文献[12]利用无迹卡尔曼滤波(Unscented Kalman Filter，UKF)优化RSSI测距值，并根据实际的定位精度需求使用不同密度的锚节点进行定位。文献[13]利用概率分布的方式对节点间的测距误差进行修正，并根据质心算法求出定位结果。但由于煤矿井下环境复杂，利用上述定位方法并不能得到精确的定位结果，为此，本文提出了一种基于改进高斯混合滤波的矿井加权质心定位算法，以提高井下定位精度。首先根据聚类思想，利用最大期望(Expectation Maximization, EM)算法[14]对同一节点产生的RSSI值进行聚类，即根据高斯混合滤波模型(Gaussian Mixture Model，GMM)处理测量数据，将其划分为多个高斯概率密度函数模型，并计算不同模型下的赤池信息量准则(Akaike Information Criterion, AIC)[15]值，将具有最小AIC值的分布当作处理RSSI测量数据的滤波分布，优化RSSI测量值，求出节点间的精确距离，对由质心算法求出的定位结果进行加权处理，得到未知节点的最终坐标。相比于现有的同类型煤矿井下定位算法，本文提出的改进算法能够更加精确地估计井下目标的位置坐标。
1 基于改进高斯混合滤波的矿井加权质心定位算法
1.1 基于高斯混合滤波模型的RSSI测距优化
1.1.1 矿井信号衰减模型
在RSSI测距中，当测量节点间的距离增加时，信号强度逐渐下降。常用的煤矿井下信号衰减模型为
(1)
式中：RSSI1为接收信号强度值；RSSI0为参考距离为d0时的RSSI值，d0的值常设置为1 m；ξ为无线信号衰减因子；d1为测量节点间的实际距离；ε为高斯随机参数，其平均值为0。
由于煤矿井下巷道环境复杂，RSSI信号容易受到环境噪声、多径衰减、障碍物、温度和湿度的影响，导致产生异常的RSSI值，影响定位精度。常用的RSSI滤波算法主要有高斯滤波、中值滤波等，但它们往往只能降低短期环境干扰对RSSI值的影响，对于多径衰减等因素造成的测量值异常效果不明显。本文利用高斯混合模型处理RSSI采样数据，以获得理想的RSSI测距值。
1.1.2 高斯混合滤波模型
高斯混合滤波模型可分为3种，即RSSI测量数据分布模型分为以下3种：1个Component(Component1)、2个Component(Component2)、3个Component(Component3)。当采样值的分布模型大于3个Component时，使用3个Component滤波模型对采样值进行处理效果更佳。
(1) 具有1个Component的高斯滤波模型。模型的概率密度函数为
(2)
其中：
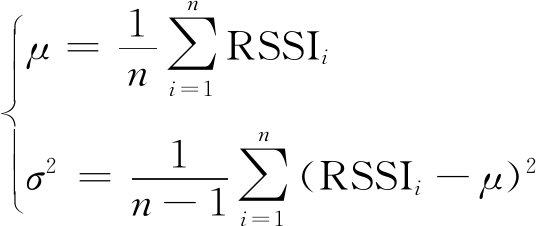
(3)
式中：μ为RSSI样本均值；n为RSSI测量数据的个数；σ2为RSSI样本方差；RSSIi为第i次测量得到的RSSI信号强度值。
根据经验，当f(RSSI)<0.6时，RSSI测量值误差较大，应该舍弃；当f(RSSI)≥0.6时，RSSI测量值的偏差较小，应该保留，并对其求平均值，得到优化后的RSSI值。
(2) 具有2个Component的高斯混合滤波模型。对于包含2个Component的高斯混合滤波模型，利用EM算法对RSSI测量值进行聚类处理，即使用EM算法中的E-Step算法和M-Step算法分别计算RSSI测量值的后验概率以及概率密度函数，并根据后验概率重新对RSSI测量数据进行聚类处理。重复执行以上2种算法，直到RSSI数据的似然性达到最大。
利用E-Step算法计算RSSI测量数据的后验概率，RSSIi属于Component1和Component2的后验概率分别为
(4)
式中τ1为Componet1对应的高斯滤波模型的权重。
根据M-Step算法计算RSSI测量数据的均值μ、方差σ2、概率密度函数
和
进而得到p(RSSIi)1,p(RSSIi)2的值。如果p(RSSIi)1>p(RSSIi)2，则该RSSI值属于Component1，算法重复执行时，RSSIi会被分到Component1中；如果p(RSSIi)1<p(RSSIi)2，则该RSSI值属于Component2，算法重复执行时，RSSIi会被分到Component2中。
对RSSI测量数据进行遍历操作，直到
以及τ1收敛。
(3) 具有3个Component的高斯混合滤波模型。类似于具有2个Component的高斯混合滤波模型，对于具有3个Component的高斯混合滤波模型而言，根据E-Step算法和M-Step算法计算RSSIi属于Component1,Component2,Component3的后验概率:
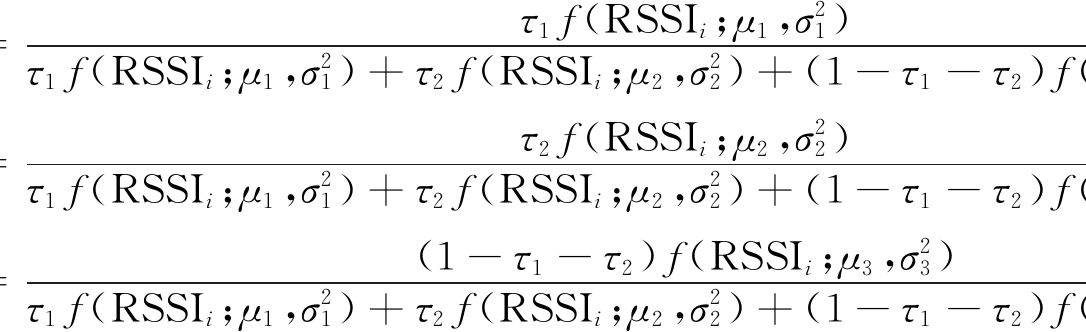
(5)
式中τ2为Componet2对应的高斯滤波模型的权重。
比较这3个概率值的大小，确定每个RSSI值的归属，并对RSSI测量数据进行遍历操作，直到
以及τ1,τ2收敛。
1.1.3 最佳高斯滤波模型选取
AIC可用于精准评估模型的数据拟合结果，以便选择最佳滤波模型。AIC可以表示为
AIC=2c-2lnL
(6)
式中：c为高斯滤波模型中参数的数量；L为似然函数。
选择AIC值最小的分布模型作为最佳滤波模型。
具有1个Component的高斯分布共有2个参数：
所以c=2，且
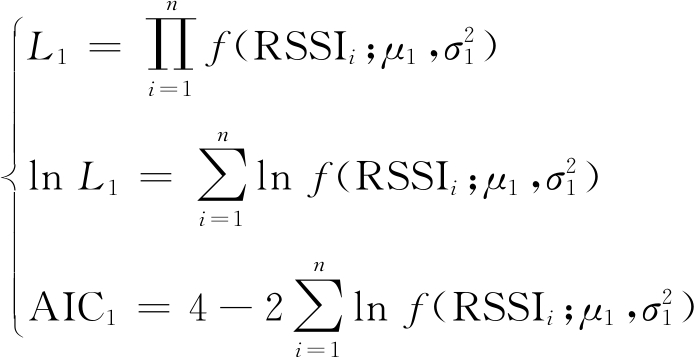
(7)
具有2个Component的高斯混合分布共有5个参数：
所以c=5，且
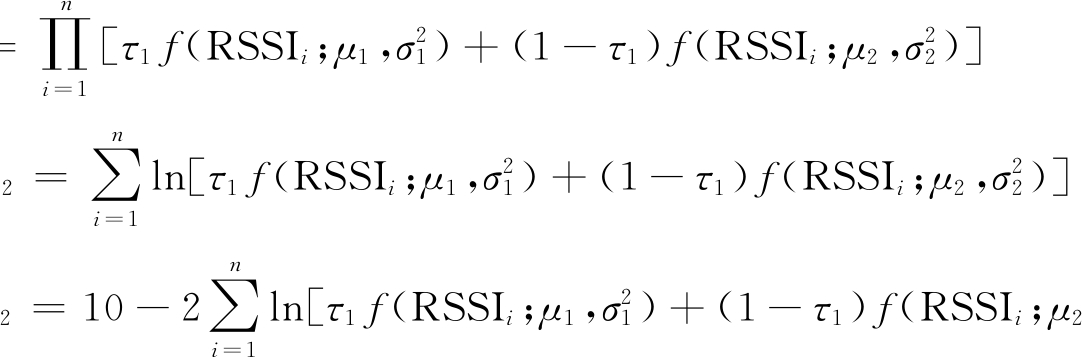
(8)
具有3个Component的高斯混合分布共有8个参数：
所以c=8，且
(9)
计算出每种情况下的AIC值，将具有最小AIC值的分布当作处理RSSI测量值的滤波分布，计算出相对应的Component平均值，并将其作为优化后的RSSI值代入信号衰减模型中计算节点间的距离。
1.2 改进的加权质心定位算法
1.2.1 质心算法
假设未知节点的坐标为(x,y),在未知节点通信半径内的m个锚节点的坐标分别为(x1,y1),(x2,y2),…,(xm,ym)，经过混合高斯滤波算法处理后的锚节点到未知节点的距离分别为d1,d2,…,dm，则有
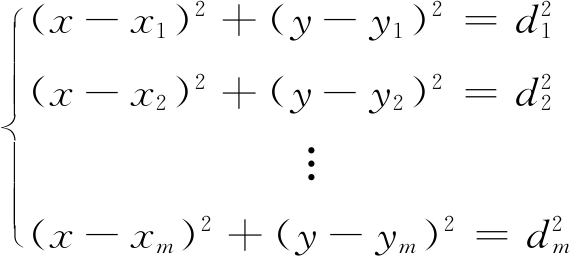
(10)
式(10)中，前m-1个等式分别减去最后一个等式，经过整理可以表示为AX=b的形式，且A=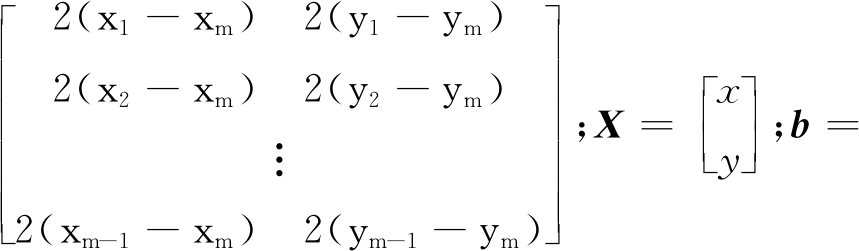
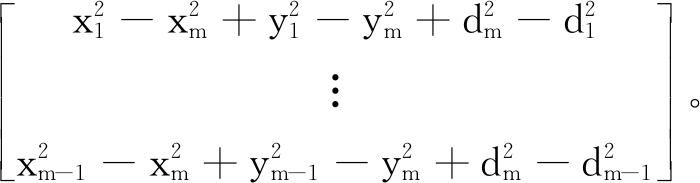
根据最小二乘法，未知节点的估计坐标为
X=(ATA)-1ATb
(11)
利用RSSI测距进行定位时，根据单组测量数据得到的未知节点的定位结果误差较大，考虑到计算复杂度和定位开销问题，一般选取3组测量数据进行重复定位，求出定位结果为
(12)
式中：(x0,y0)为利用质心算法计算出来的坐标；
分别为根据3组数据计算得到的初始坐标。
1.2.2 改进加权质心算法
在式(12)中，根据3组测量数据求出的定位坐标在最终坐标计算时所占权重是相同的。但正如式(11)所示，b值越精确，未知节点的计算坐标越接近真实坐标；b值误差越大，计算结果偏离真实坐标的程度就越大。因此，本文利用加权质心算法计算未知节点的最终坐标。定义权值因子ωi为未知节点初始坐标和真实坐标之间误差值的倒数：
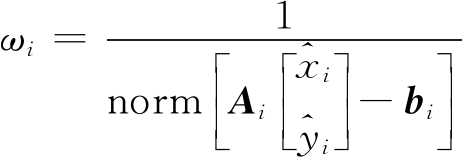
(13)
式中：
表示根据第i组数据计算得到的初始坐标；Ai，bi表示根据第i组数据计算得到的方程系数；norm()表示二范数。
由加权质心算法求出未知节点的最终坐标为
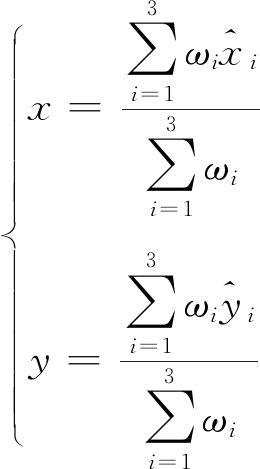
(14)
在改进的加权质心算法中，不同初始定位结果对最终定位结果的影响各不相同，误差大的初始结果所占权值较小，误差小的初始结果所占权值较大，使得算法的定位精度有了很大的提升。
1.3 算法步骤
基于改进高斯混合滤波的矿井加权质心定位算法具体步骤如下：
(1) 在设定的阈值范围内，每个未知节点接收并存储来自锚节点的RSSI测量数据。
(2) 利用EM算法对未知节点的相应RSSI测量数据进行聚类，并将其划分为多个高斯概率密度函数模型。
(3) 计算不同高斯概率密度函数模型下的AIC值，将具有最小AIC值的分布当作处理RSSI测量数据的滤波分布，以优化RSSI测量数据，得到精确的测距值。
(4) 根据质心算法，选取3组测距值计算未知节点的初始坐标。
(5) 计算未知节点初始坐标和真实坐标之间的误差值，将其倒数作为权值因子，并根据加权质心算法计算未知节点的最终坐标。
2 仿真结果分析
2.1 RSSI测距优化
为了验证本文的算法性能，进行了仿真实验。在20 m×2.5 m的矩形仿真区域内设置4个锚节点，坐标分别为A(0,0)、B(14,0)、C(20,2.5)、D(7,2.5)，并设置8个未知节点,如图1所示。为保证RSSI测量的准确性，根据式(1)，由最小二乘法拟合测量数据，得到信号传播距离为d时的距离损耗模型为
(15)
仿真测试中，每个未知节点收集来自锚节点的200个RSSI值，分别利用高斯滤波算法和本文提出的改进高斯混合滤波算法对这些RSSI值进行处理，得到优化的RSSI值，并根据式(15)计算相应的距离，由式(16)计算测距误差:
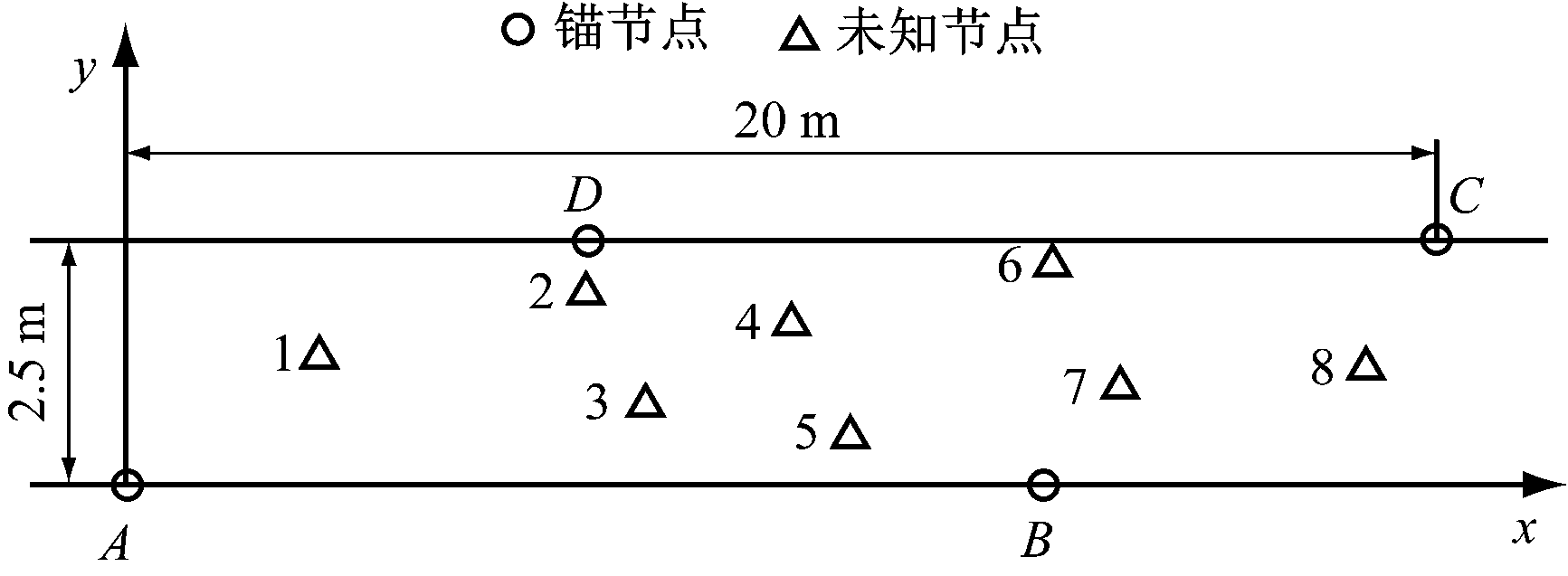
图1 RSSI数据滤波优化实验布局
Fig.1 Experiment layout of RSSI data filtering optimization
Δd=|drel-dest|
(16)
式中：Δd为测距误差；drel和dest分别为未知节点和锚节点之间的实际距离和测量距离。
表1为经过2种滤波算法处理后计算得到的锚节点和未知节点间的平均测距误差。从表1可看出，高斯混合滤波算法对于RSSI数据的滤波效果比经典高斯滤波算法好，利用经典高斯滤波算法得到的平均测距误差为0.81 m，利用高斯混合滤波算法得到的平均测距误差为0.62 m，其测距精度比经典高斯滤波算法提高了30.6%。
表1 经2种滤波方法处理后计算得到的锚节点和未知节点间的平均测距误差
Table 1 Average ranging error between anchor nodes and unknown nodes calculated by two filtering methods
2.2 仿真结果分析
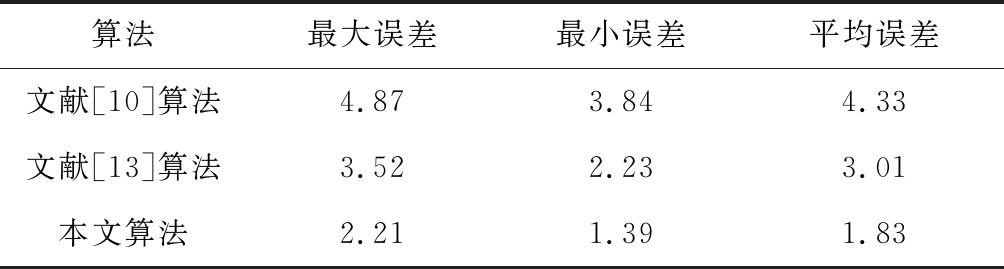
在上述条件下对本文定位算法、文献[10]算法、文献[13]算法进行仿真比较。为了减小算法的偶然性带来的误差，将各个算法重复运行50次，取平均值作为最终的仿真结果。利用3种算法得到的各未知节点误差如图2所示，3种算法的最大误差、最小误差以及平均误差见表2。对比可知，文献[10]算法的最大误差为4.87 m，最小误差为3.84 m，平均误差为4.33 m，定位结果误差较大。文献[13]算法的最大误差为3.52 m，最小误差为2.23 m，平均误差为3.01 m。本文算法的最大误差为2.21 m，最小误差为1.39 m，平均误差为1.83 m。本文算法的定位误差最小，且整体的定位效果更加稳定。本文算法利用高斯混合滤波处理RSSI测量值，减小了测距误差，并结合带有权值的质心算法求出未知节点的坐标，使得最终的定位结果精度更高。
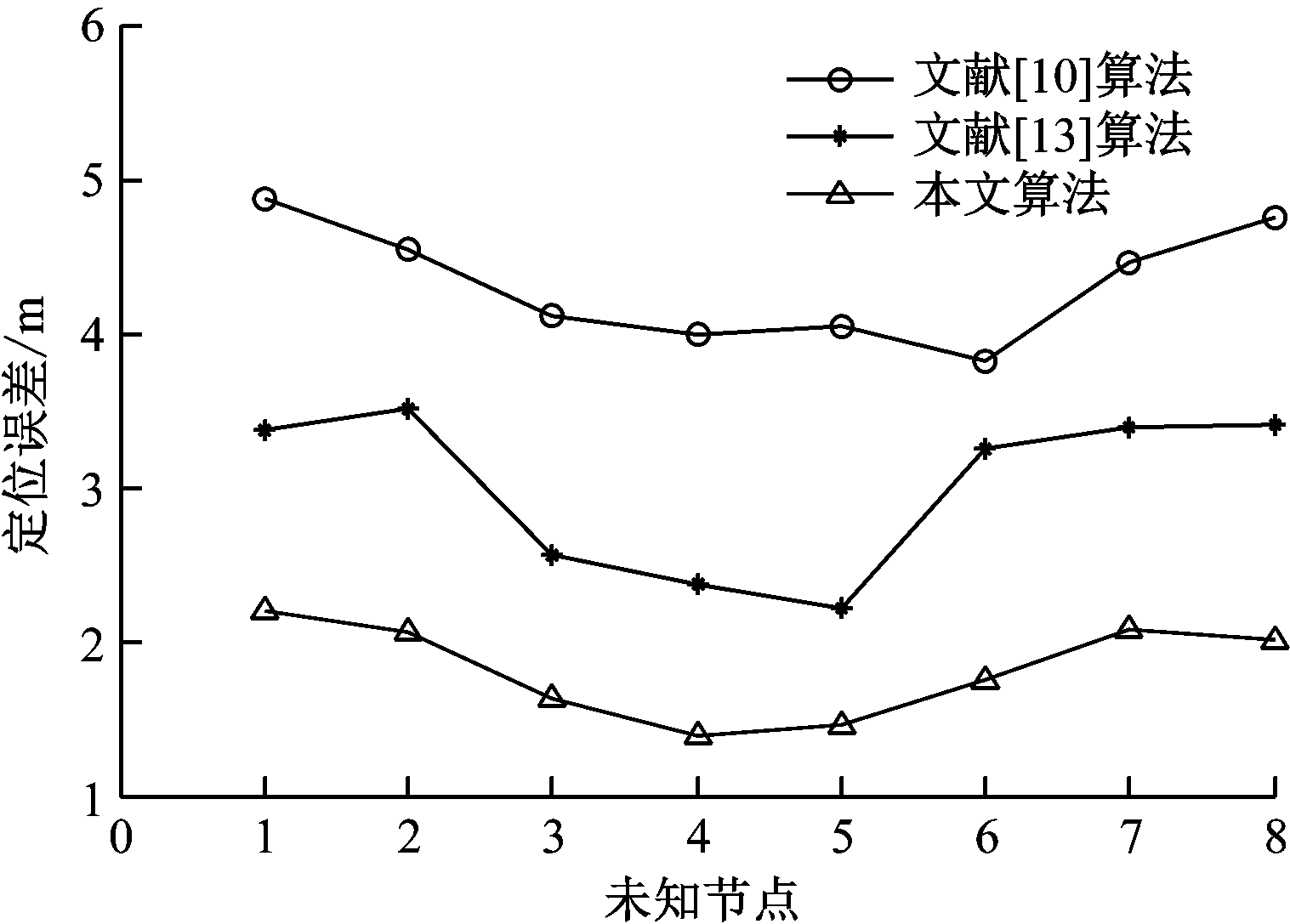
图2 3种算法定位误差仿真结果
Fig.2 Positioning error simulation results of three kinds of algorithms
表2 3种算法定位误差比较
Table 2 Positioning error comparison of three kinds of algorithms m
3 实验结果分析
3.1 实验场景布置
在长为20 m、宽为2.5 m的模拟巷道内(图3)进行数据采集实验。利用CC2530测距节点进行RSSI信号的发射与接收，在模拟巷道两侧分别放置2个锚节点，中间任意位置放置8个未知节点。为了使RSSI信号更好地传输与接收，所有节点均放置在高为1.5 m的支架上。
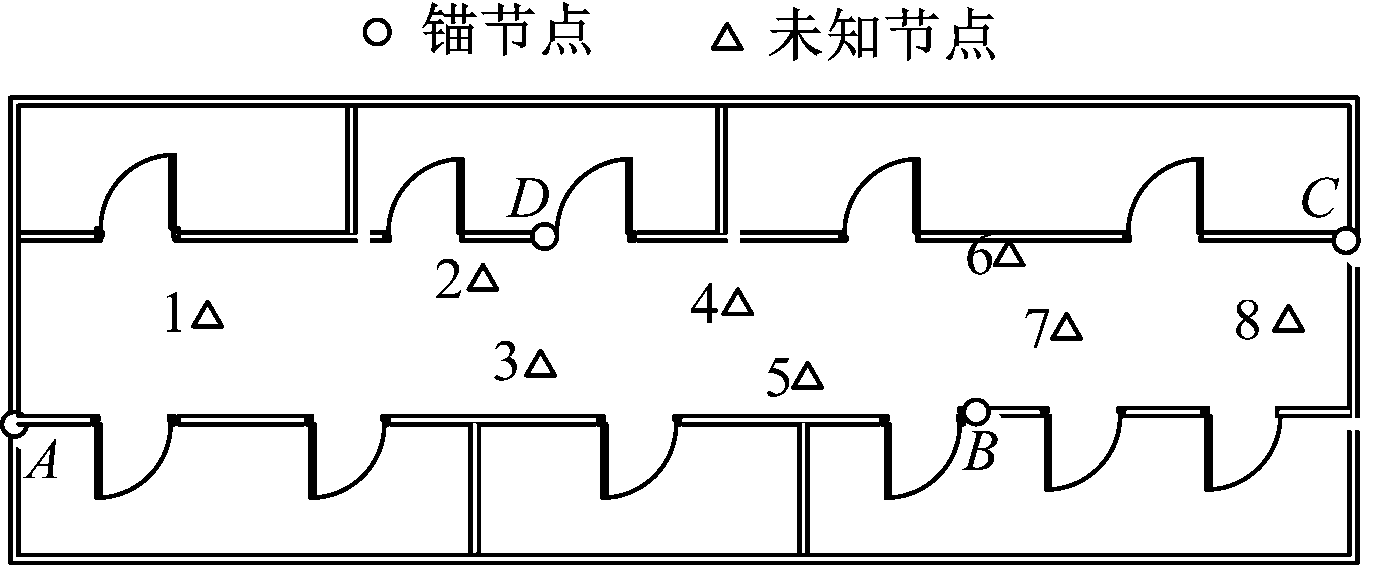
图3 RSSI数据采集模拟巷道
Fig.3 Simulation roadway of RSSI data collection
3.2 实验结果分析
将未知节点接收到的RSSI数据导入到3种定位算法中，可计算得到每个未知节点的定位坐标及定位误差，如表3和图4所示。由表3和图4可知，利用本文算法求出的未知节点的坐标误差始终小于其余2种算法求得的坐标误差。当未知节点的实际坐标为(11 m,1.7 m)时，本文算法计算得到的坐标为(12.5 m,0.9 m)，误差为1.70 m；文献[10]算法计算得到的坐标为(8.1 m,3.7 m)，误差为3.52 m；文献[13]算法计算得到的坐标为(8.7 m,0.8 m)，误差为2.47 m。实验得到的本文算法的最大误差和最小误差与仿真结果相一致，本文算法可以获得更高的定位精度。
表3 未知节点实际坐标与计算坐标对比
Table 3 Comparison of actual coordinates and calculated coordinates of unknown nodes m
图4 3种算法定位误差实测结果
Fig.4 Positioning error measurement results of three kinds of algorithms
4 结语
提出了一种改进高斯混合滤波的矿井加权质心定位算法，以提高煤矿井下目标的定位精度。该算法利用高斯混合滤波模型处理同一节点接收到的RSSI测量数据，根据数据的特征以及赤池信息量准则选择最合适的滤波模型对数据进行优化，得到精确的节点间测量距离，将未知节点初始坐标和真实坐标间的误差值作为权值因子，结合质心定位算法计算得到未知节点的最终坐标。仿真与实验结果表明，该算法的平均定位误差约为1.83 m，能够满足矿井巷道中人员和设备的定位需求。
参考文献（Ｒｅｆｅｒｅｎｃｅｓ）：
[1] 王红军,周宇,王伦文.基于SVR-Kriging插值的矿井工人二维指纹定位数据库构建算法[J].电子与信息学报,2017,39(11):2571-2578.
WANG Hongjun,ZHOU Yu,WANG Lunwen.Establishment algorithm of two dimensional fingerprint database for mine workers based on SVR-Kriging interpolation[J].Journal of Electronics & Information Technology,2017,39(11):2571-2578.
[2] HAN D S,YANG W,LIU X,et al.A weighted centroid localization algorithm based on received signal-strength indicator for underground coal mine[J].Journal of China Coal Society,2013,38(3):522-520.
[3] 龙佳,张然,闫玉萍,等.基于nanoPAN5375的煤矿井下一维目标跟踪定位系统[J].煤矿安全,2017,48(2):105-108.
LONG Jia,ZHANG Ran,YAN Yuping,et al.One-dimensional target tracking and positioning system in coal mine based on nanoPAN5375[J].Safety in Coal Mines,2017,48(2):105-108.
[4] 谢芝玉,刘雄飞,胡志坤.基于Taylor展开的UWB井下定位算法研究与实现[J].计算机工程与应用,2017,53(2):231-235.
XIE Zhiyu,LIU Xiongfei,HU Zhikun.Research and design of UWB underground coal mine positioning method based on Taylor algorithm[J].Computer Engineering and Applications,2017,53(2):231-235.
[5] ZAIDI S,ASSAF A E,AFFES S,et al.Accurate range-free localization in multi-hop wireless sensor networks[J].IEEE Transactions on Communications,2016,64(9):3886-3900.
[6] SHUAI H,GONG Z,MENG W,et al.Automatic precision control positioning for wireless sensor network[J].IEEE Sensors Journal,2016,16(7):2140-2150.
[7] WANG X,GAO L,MAO S,et al.CSI-based fingerprinting for indoor localization:a deep learning approach[J].IEEE Transactions on Vehicular Technology,2017,66(1):763-776.
[8] 王峰,尚超,籍锦程,等.基于TDOA和AOA的煤矿井下三维定位算法[J].工矿自动化,2015,41(5):78-82.
WANG Feng,SHANG Chao,JI Jincheng,et al.Three-dimensional positioning algorithm based on TDOA and AOA in coal mine underground[J].Industry and Mine Automation 2015,41(5):78-82.
[9] 李论,张著洪,丁恩杰,等.基于RSSI的煤矿巷道高精度定位算法研究[J].中国矿业大学学报,2017,46(1):183-191.
LI Lun,ZHANG Zhuhong,DING Enjie,et al.Precision positioning algorithm in coal mine tunnel based on RSSI[J].Journal of China University of Mining & Technology,2017,46(1):183-191.
[10] 韩东升,杨维,刘洋,等.煤矿井下基于RSSI的加权质心定位算法[J].煤炭学报,2013,38(3):522-528.
HAN Dongsheng,YANG Wei,LIU Yang,et al.A weighted centroid localization algorithm based on received signal strength indicator for underground coal mine[J].Journal of China Coal Society,2013,38(3):522-528.
[11] XING Zhipeng,LI Chunwen,LU Sicong,et al.Coal mine underground personnel localization algorithm based on LQI filter and joint parameters estimation[J].Journal of China Coal Society,2017,42(6):1628-1633.
[12] 余修武,刘琴,张枫,等.基于UKF的深井监测移动节点定位算法[J].中国安全生产科学技术,2017,13(9):72-76.
YU Xiuwu,LIU Qin,ZHANG Feng,et al.Positioning algorithm for mobile nodes monitoring in deep mine based on UKF[J].Journal of Safety Science and Technology,2017,13(9):72-76.
[13] 候倍倍,宋玉龙,曹硕.基于RSSI的偏移误差修正的井下定位算法[J].工矿自动化,2017,43(11):63-69.
HOU Beibei,SONG Yulong,CAO Shuo.An underground positioning algorithm of offset error correction based on RSSI[J].Industry and Mine Automation,2017,43(11):63-69.
A,ROGALEWICZ M,DIERING M.Application of expectation maximization method for purchase decision-making support in welding branch[J].Management & Production Engineering Review,2016,7(2):29-33.
[15] 贺小星,花向红,鲁铁定,等.时间跨度对GPS坐标序列噪声模型及速度估计影响分析[J].国防科技大学学报,2017,39(6):12-18.
HE Xiaoxing,HUA Xianghong,LU Tieding,et al.Effect of time span on GPS time series noise model and velocity estimation[J].Journal of National University of Defense Technology,2017,39(6):12-18.