0 引言

UWB(Ultra Wide Band,超宽带)技术具有定位精度高、功耗低、穿透性好、抗干扰能力强等优点，广泛应用于井下人员、大型设备及井下机器人定位服务[1-2]。然而，狭小而不规则的井下通信环境及矿车等容易导致电磁干扰和多径传播，且测距设备自身也存在误差[3-4]，导致了UWB测距会存在一定的误差。三边定位算法是一种常见的基于UWB的TOA(Time of Arrival，到达时间)定位算法[1]。理想的三边定位算法中，被测目标的位置存在唯一的解，通过求解一个二元二次方程即可求得，然而，由于UWB测距存在一定的测量误差，只能求得被测目标的最优解，属于典型的二元二次方程优化问题。针对二元二次方程优化问题，方焕阳等[5]使用Fang算法确定定位目标的坐标，但Fang算法是一种具有解析表达式解的算法，容易产生双解，且在某个测量值存在较大误差时，定位精度大幅降低。董长春等[6]采用Chan算法来计算定位目标的近似坐标，该算法通过加权最小二乘法来求解最优值，在非视距误差大量存在的情况下存在精度不高的问题。包建军等[7]通过最小二乘定位算法来确定定位目标的位置，算法实现简单，但容易求出次优解，精度有待提升。张宝军[8]利用泰勒迭代算法进行目标定位，但泰勒迭代算法对初始值的选取要求高，初始值选取不好,容易产生局部最优解。此外，还有学者认为，通过增加测量节点的数量也可提高UWB的测量精度，但会相应地增加成本[9-10]。

针对现有基于UWB的井下定位算法存在算法复杂且求解值不是全局最优的问题，本文选用DW1000测距芯片，通过双边双向测距方法实现节点间距离的测量，提出了一种基于UWB的三边定位改进算法。该算法以求解二元二次方程最优解为目标，设定优化目标函数，将坐标二维化处理，筛除测量过程中产生的无效数据，确定有效搜索区域，并在有效搜索区域内进行全局遍历，找到最优定位坐标，解决了求解值不是全局最优的问题。该算法把浮点数转换成整数处理，有利于降低算法复杂度。

1 高精度测距方案

为测得参考节点与被测目标之间的真实距离，为后续算法中数据筛选等内容提供依据，本文设计了基于DW1000的高精度测距方案。

1.1 硬件结构

与同类UWB定位芯片相比，DW1000芯片由于测距精度高，在室内测距领域得到了广泛应用。基于DW1000芯片设计了如图1所示的测距方案。设备包括参考节点和目标节点。其中，参考节点为全功能设备，既可实现UWB无线通信，也可实现WiFi通信，作为网络协调器使用，而目标节点属于简化功能设备，只具有UWB无线通信功能。

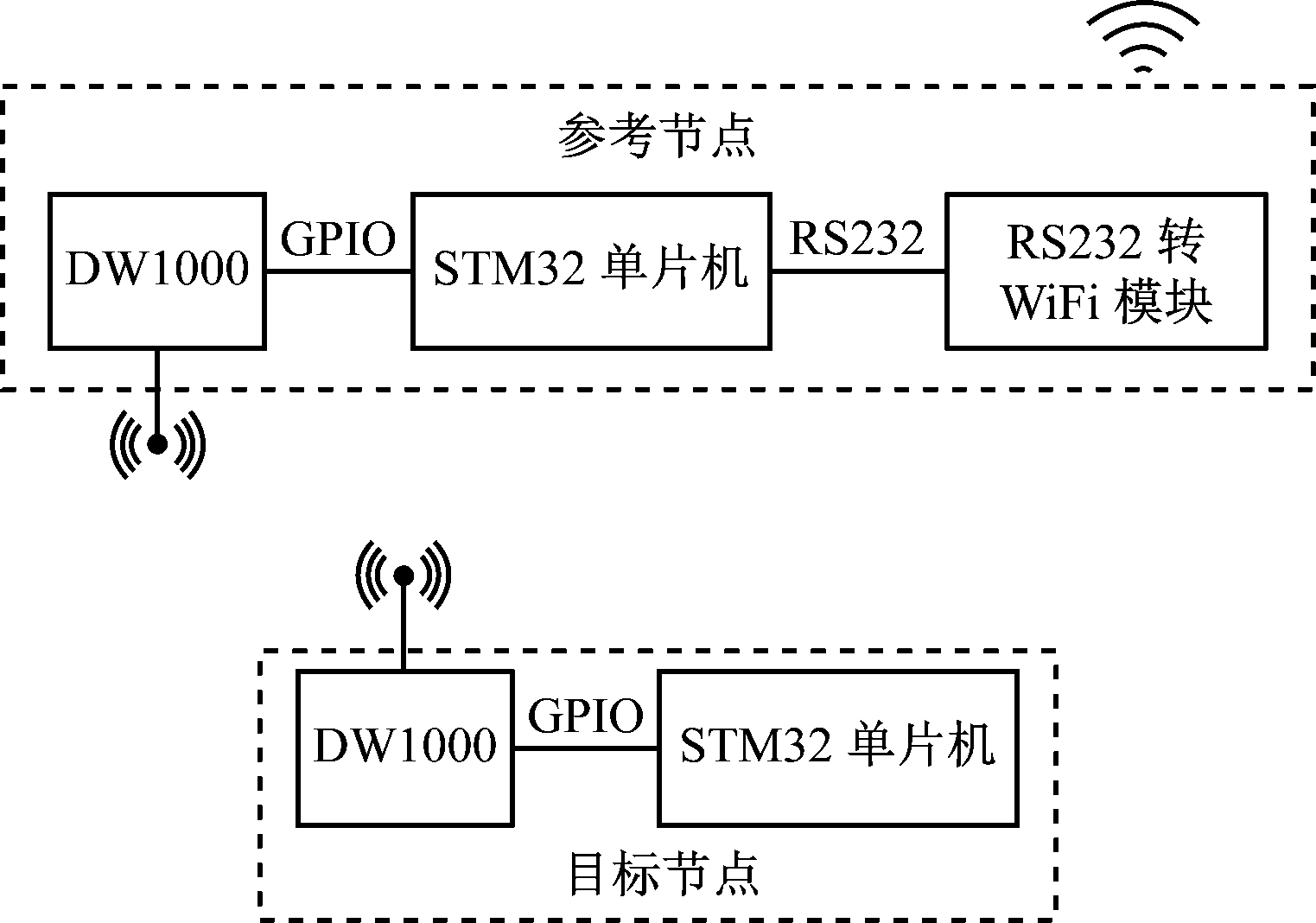
图1 高精度测距方案硬件结构
Fig.1 Hardware structure of high precision ranging scheme

1.2 测距原理与实现

采用双边双向测距方法实现参考节点与被测目标之间的测距，可避开收发节点时间同步的问题，其测距过程如图2所示。其中，TX代表发送，RX代表接收。

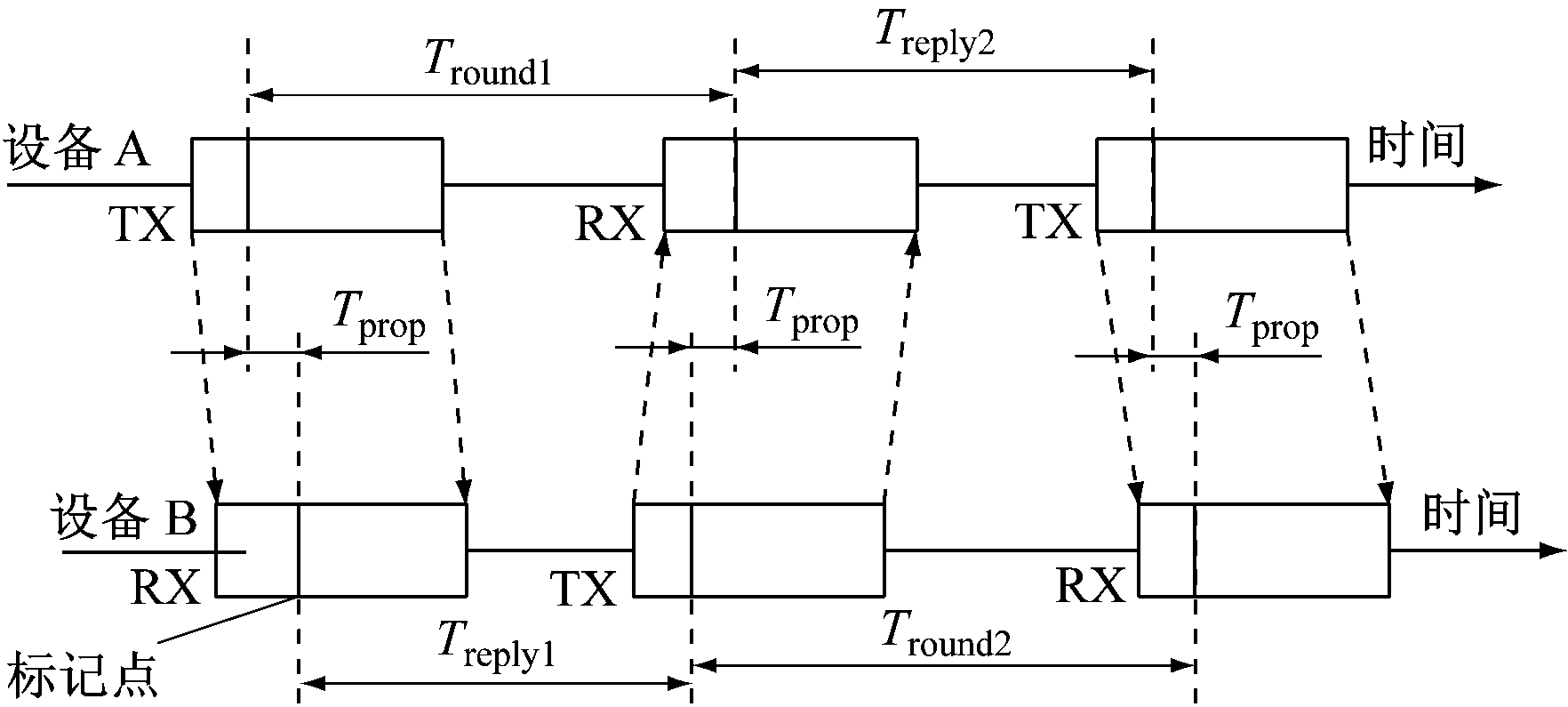
图2 双边双向测距方法测距过程
Fig.2 Ranging process of bilateral two-way ranging method

具体测量过程如下：

(1) 设备A主动发送一个测距包，并记录发送时间T1，完成后等待数据接收。

(2) 设备B事先准备数据接收，收到测距包后，记录到达时间T2。

(3) 设备B在间隔时间Treply1后，发送响应包至设备A，将T2+Treply1时刻记为T3。

(4) 设备A收到设备B发送过来的响应包时，记录到达时间，记为T4。

(5) 设备A在间隔时间Treply2后，发送结束包，将T4+Treply2时刻记为T5。

(6) 设备B收到设备A发送过来的结束包时，记录到达时间T6。

(7) 在忽略响应时间的情况下，计算出4个时间差:

(1)

将上述4个时间差代入式(2)，计算出飞行时间，然后乘以光速即可得到测量距离。

(2)

2 改进的三边定位算法

2.1 三边定位算法原理

三边定位算法模型如图3所示，已知3个参考节点S1,S2和S3的坐标分别为(x1,y1),(x2,y2),(x3,y3)，一个目标节点T0的坐标为(x,y)，根据UWB测距方法，测量出被测目标T0到3个参考节点的距离分别为d01,d02和d03。

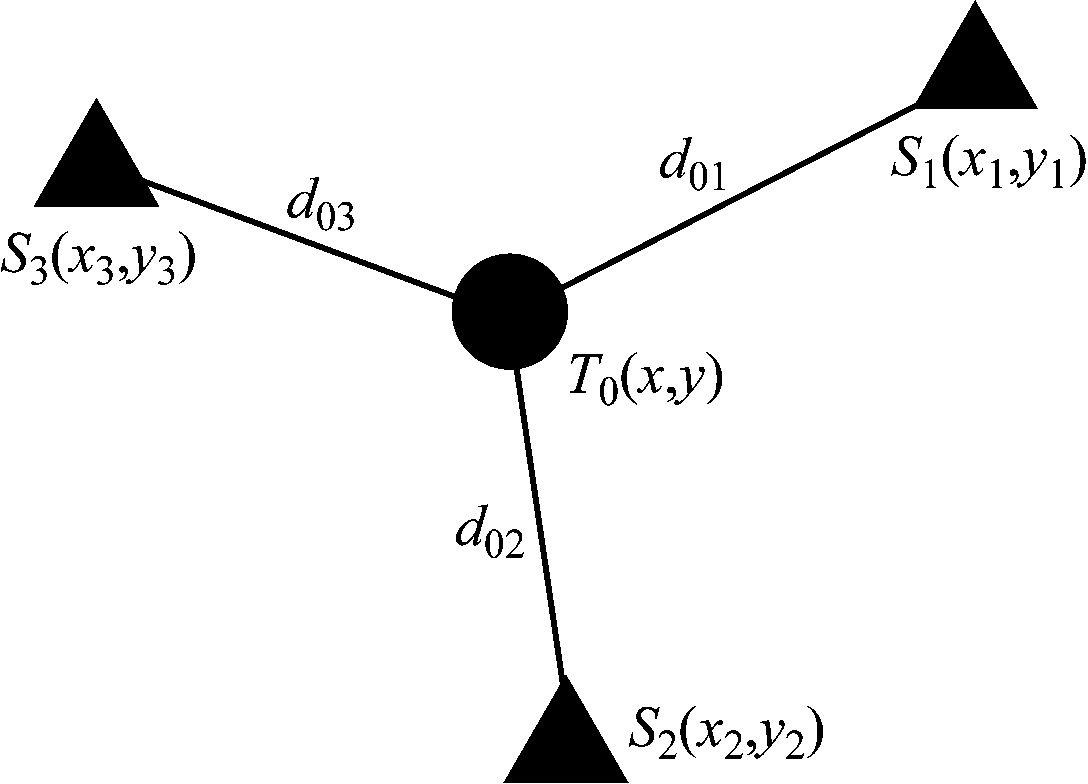
图3 三边定位算法模型
Fig.3 Model of trilateral positioning algorithm

在二维平面坐标系下，4个坐标之间存在如下关系：

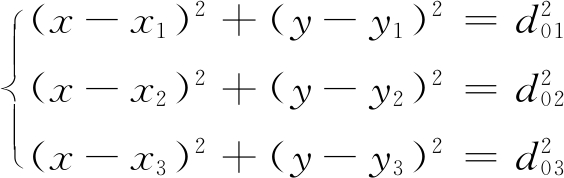
(3)

理想的三边定位算法如图4所示，即测量出的d01,d02和d03没有误差，这时可以求得唯一正确的解T0的坐标(x,y)。

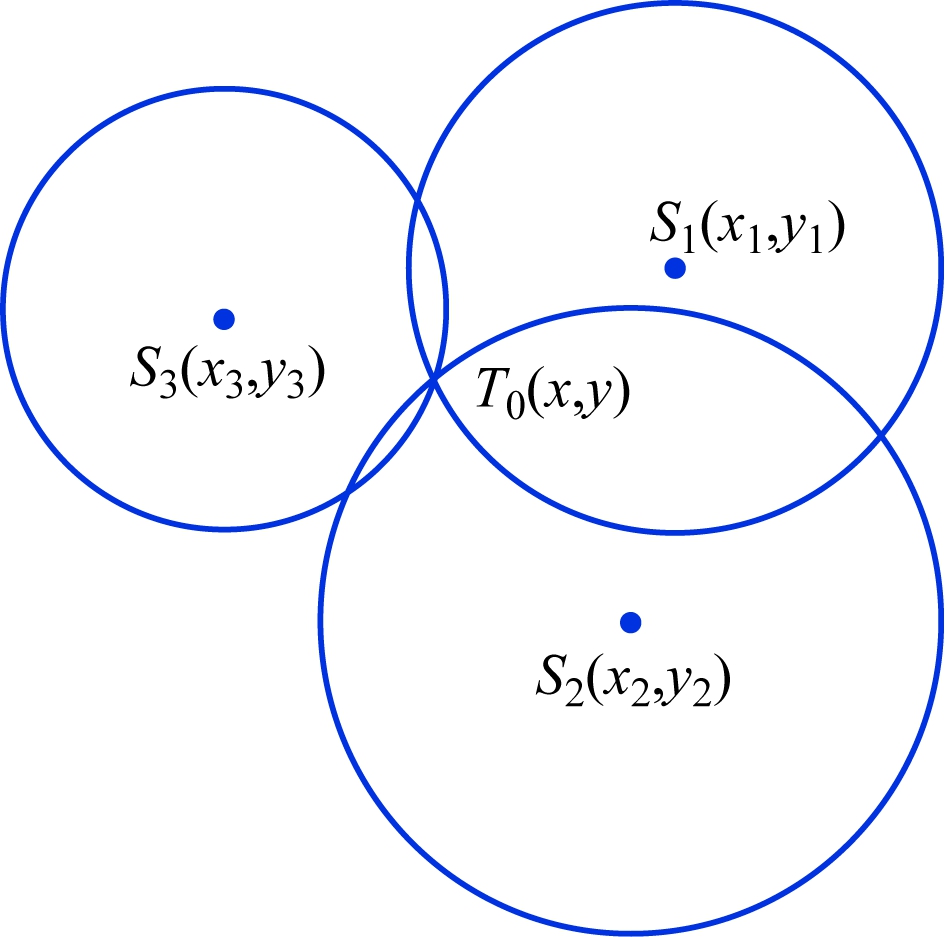
图4 理想的三边定位算法
Fig.4 Ideal trilateral positioning algorithm

2.2 改进的三边定位算法原理

真实的测距是存在误差的，产生误差的原因包括测距设备本身的误差，如测距芯片DW1000和定位芯片JR3401精度为厘米级；此外，矿井环境复杂，矿车经常采用钢铁外壳，这些因素都会影响电磁波穿透性和传输效果，产生不确定的测量误差。由于上述环境和设备响应时间等原因，测量值存在正向误差，即测量值偏大，形成如图5所示的效果。不难看出，目标节点T0的处于阴影区域，这样需要在阴影区域内找到最优值。

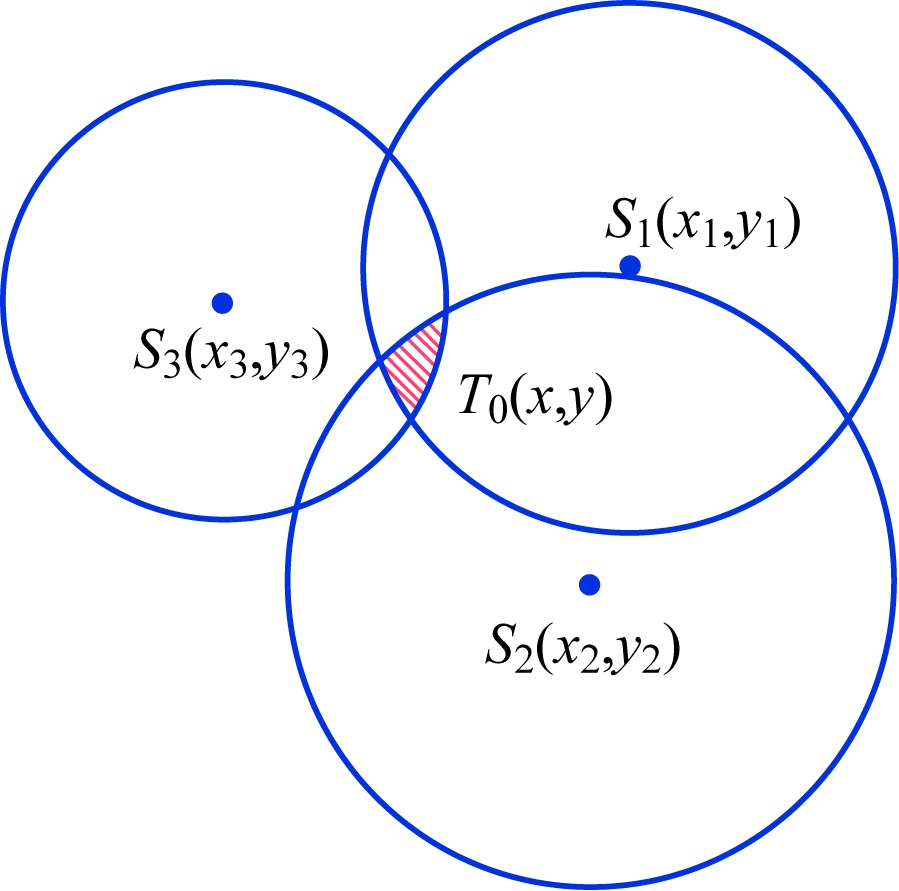
图5 实际的三边定位算法
Fig.5 Actual trilateral positioning algorithm

针对图5存在的问题，学者研究了质心泰勒混合算法[10]、改进质心算法[11]、加权三边算法[12]等。本文采用式(4)所示的目标函数，以此为优化目标，在此基础上找到最优解，确定目标节点T0的坐标(x,y)。

(4)

2.3 改进算法实现

以式(4)为优化目标，改进算法的具体实现步骤如下：

(1) 对坐标进行二维栅格化处理：将测量值转换成整数，且要求转换后单位相同，如将860.5 cm转换成8 605 mm，720 cm转换成7 200 mm。在此基础上绘制坐标，如图6所示，采用二维数组存储数据，将数组内的初始值全部赋为0。

图6 栅格化坐标
Fig.6 Rasterized coordinates

(2) 筛除无效数据：取参考节点i的坐标(xi,yi)和参考节点j的坐标(xj,yj)，并计算出它们之间的距离dij。测量正常的数据应该全部满足如下条件：

d0i+d0j>dij i,j=1,2,3,且i≠j

(5)

一旦发现测量距离之间存在式(6)所示关系,则此测距产生的数据为无效数据，结束本次运行，记录测量错误数据，便于后续分析。

d0i+d0j≤dij(i,j=1,2,3,且i≠j)

(6)

(3) 确定有效区域：如图5所示，有效区域内栅格点应满足到圆心(参考节点)的距离都小于或等于圆心半径(测量距离)这个条件，因此，遍历所有栅格，取出坐标值，看是否满足该条件，如果满足，代表该栅格属于有效区域，将该栅格内的值设为1，否则无需修改该栅格内的值。

(4) 寻找最优值：取有效区域(值为1)内的各栅格点坐标值，赋值给式(4)中的x和y，计算出目标函数值Zmin，并记录坐标值x和y。对有效区域内所有点进行遍历，一旦出现更小的Zmin，则更新Zmin值，同时更新坐标x和y。

(5) 遍历完成后，可得到目标节点T0的坐标(x,y)。

上述算法至少需要3个参考节点，为了进一步提高测量精度，还可增加参考节点的数量。这时可将所有参考节点进行三三组合，每个组合得到一组目标节点T0的坐标(x,y)，所有组合计算结束后，将计算得到的坐标计算平均值，最终得到目标节点T0的坐标(x,y)。

3 实验与分析

为了验证基于UWB的三边定位改进算法的有效性，设计了如图7所示的模拟测试方案。模拟巷道宽约4 m，考虑到UWB无线通信距离，在模拟巷道的两侧每隔40 m布置一个参考节点。各参考节点与目标节点之间通过UWB进行通信，参考节点与上位机之间通过WiFi方式进行通信，上位机用于接收各参考节点发送过来的测量数据，并验证算法的有效性。当需要增加参考节点时，可加大参考节点的布设密度。

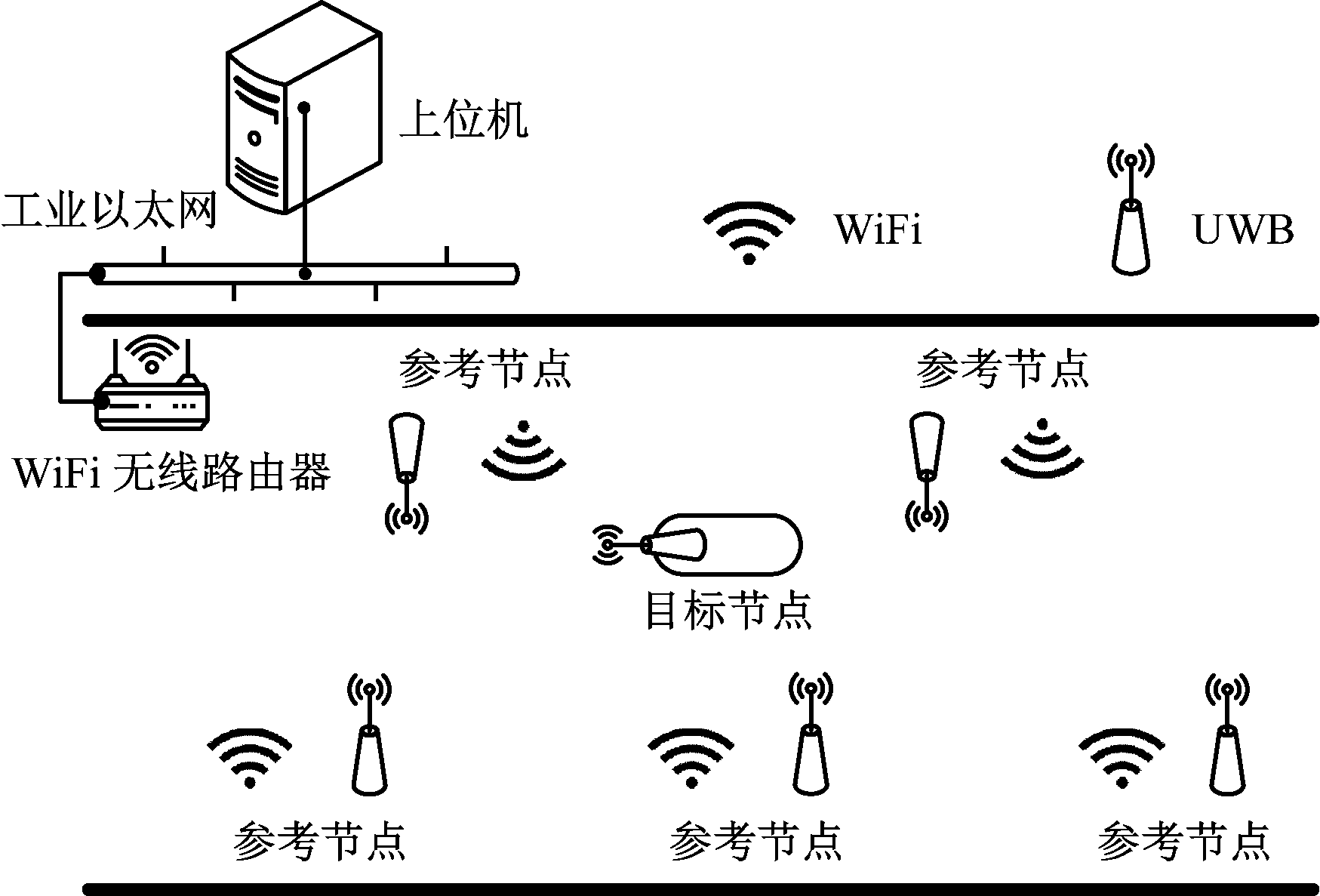
图7 测试方案
Fig.7 Test scheme

本文算法与其他同类算法在相同情况下的定位误差比较如图8所示。定位误差为测量值与标定距离(真实值)之间差值的绝对值。分别采用加权三边定位算法[12]、泰勒算法以及本文算法求得7个不同测量点对应的定位误差，再分别对7个定位误差求平均值，得到加权三边定位算法[12]、泰勒算法以及本文算法的平均定位误差，结果分别为0.717,0.633,0.45 m。对比发现，加权三边定位算法略优于泰勒算法，而本文算法平均定位误差最小。

图8 不同算法测量误差
Fig.8 Measurement error of different algorithms

设置不同参考节点个数对同一测量点进行测量,平均定位误差如图9所示。从图9可看出，通过增加参考节点数量能够提高测量精度，开始效果非常明显，但到6个参考节点之后，误差基本趋于稳定，改善效果不明显，应用中需根据实际情况选择参考节点数。

图9 参考节点数不同时同一测量点的测量误差
Fig.9 Measurement error of a point with different number of reference nodes

4 结语

提出了一种基于UWB的三边定位改进算法。该算法是在UWB真实测距和三边定位算法基础上，以求解一个二元二次方程最优解为目标，通过坐标二维栅格化处理，筛除掉无效测量数据，确定有效搜索区域，不仅可以大大缩小测量坐标的搜索范围，求得目标最优定位坐标，还可发现测距过程中出现的异常数据，最终达到提升井下目标定位精度的目的。实验结果表明，该算法平均误差小于加权三边定位算法、泰勒算法，定位精度提升明显；同时，该算法具有较强的实用性，通过增加参考节点数可有效提升测量精度；把浮点数转变成整数处理，降低了算法复杂度。

参考文献（Ｒｅｆｅｒｅｎｃｅｓ）：

[1] 霍振龙.矿井定位技术现状和发展趋势[J].工矿自动化,2018,44(2):51-55.

HUO Zhenlong.Status and development trend of mine positioning technology[J].Industry and Mine Automation,2018,44(2):51-55.

[2] 陈惠雄.UWB组网定位算法研究[D].广州：广东工业大学,2017:1-4.

CHEN Huixiong.Research on positioning algorithm based on UWB[D].Guangzhou:Guangdong University of Technology,2017:1-4.

[3] 丁龙.煤矿井下UWB人员定位研究[D].哈尔滨：黑龙江科技大学,2013:1-7.

DING Long.Study of UWB personnel positioning in underground coal mine[D].Harbin:Heilongjiang University of Science and Technology,2013:1-7.

[4] 陈康,包建军,王伟.一种鲁棒的矿井接近探测定位算法研究[J].工矿自动化,2018,44(6):11-15.

CHEN Kang,BAO Jianjun,WANG Wei.Research on a robust algorithm for mine proximity detection [J].Industry and Mine Automation,2018,44(6):11-15.

[5] 方焕阳,李烨.基于聚类和TDOA的无线基站定位算法研究[J].通信技术,2019,52(2):311-317.

FANG Huanyang,LI Ye.Wireless base station location algorithm based on clustering and TDOA[J].Communications Technology,2019,52(2):311-317.

[6] 董长春,周良.基于RFID及改进Chan算法的商品车定位方法[J].计算机技术与发展,2019(10):1-6.

DONG Changchun,ZHOU Liang.Commodity car location method based on RFID and improved Chan algorithm[J].Computer Technology and Development,2019(10):1-6.

[7] 包建军,霍振龙,徐炜，等.一种高精度井下人员无线定位方法[J].工矿自动化,2009,35(10):18-21.

BAO Jianjun,HUO Zhenlong,XU Wei,et al.A wireless location method with high precision for underground personnel tracking[J].Industry and Mine Automation,2009,35(10):18-21.

[8] 张宝军.基于RBF神经网络的泰勒级数展开定位算法[J].计算机工程与应用,2009,45(15):245-248.

ZHANG Baojun.Taylor-series expansion location algorithm based on RBF neural network[J].Computer Engineering and Applications,2006,45(15):245-248.

[9] 祖明浩,荣宪伟.基于内三角形质心修正-Taylor的UWB室内定位算法[J].哈尔滨师范大学自然科学学报,2018,34(6):42-47.

ZU Minghao,RONG Xianwei.UWB indoor location algorithm based on inner triangle centroid correction-Taylor [J].Natural Science Journal of Harbin Normal University,2018,34(6):42-47.

[10] 王磊,李鹏涛,贾宗璞.基于全质心-Taylor的UWB室内定位算法[J].传感器与微系统,2017,36(6):146-149.

WANG Lei,LI Pengtao,JIA Zongpu.UWB indoor location algorithm based on full centroid and Taylor [J].Transducer and Microsystem Technologies,2017,36(6):146-149.

[11] 魏培,姜平,贺晶晶,等.基于内三角形质心算法的超宽带室内定位[J].计算机应用,2017,37(1):289-293.

WEI Pei,JIANG Ping,HE Jingjing,et al.Ultra wideband indoor localization based on inner triangle centroid algorithms [J].Journal of Computer Applications,2017,37(1):289-293.

[12] 吴文健,刘瑾,李贺林，等.一种改进的加权三边定位算法[J].郑州轻工业学院学报(自然科学版),2012,27(3):83-85.

WU Wenjian,LIU Jin,LI Helin,et al.An improved weighted trilateral localization algorithm [J].Journal of Zhengzhou University of Light Industry(Natural Science Edition),2012,27(3):83-85.