0 引言
煤矿井下各种移动设备和人员的实时准确定位一直是困扰煤炭行业的重大难题[1]。当前煤矿井下定位主要采用RFID技术和WiFi技术，这2种技术的定位精度不高，误差一般在10 m甚至更高，而且不是实时系统，不能满足井下定位的实时性和精度要求[2-4]。UWB(Ultra Wide Band，超宽带)技术具有抗干扰性强、传输速率高、功率低等优点，理论上能提供厘米级甚至更高的定位精度，在解决井下精确定位问题上具有巨大的潜力。基于TOA(信号到达时间)、TDOA(信号到达时间差)的定位方法充分利用了UWB技术的优点，其定位精度与信号传输时间有关，受井下复杂环境影响小，因此适用于矿井人员精确定位。相比于TOA算法，TDOA算法不需要在定位目标与锚点之间建立时钟同步关系，只要各锚点之间时钟同步即可，实现成本较低，因此，受到的关注度更高。
文献[5-6]给出了TDOA系统定位模型及基本的求解算法，文献[7]将TDOA定位问题转换为非线性方程组求解问题，成为后续研究的基础；但上述文献均假定锚点位置已知，而在煤矿井下实际场景中，锚点位置往往难以准确获得。文献[8-9]证明了锚点位置误差影响TDOA定位算法性能的下界，并提出了一种考虑锚点位置误差的WLS(Weighted Least Squares，加权最小二乘)定位算法，但在锚点位置误差较大的条件下，算法精度显著下降。文献[10-11]结合凸优化理论中半正定规划(Semidefinite Programming, SDP)的方法，将原始定位问题转换为凸问题进行求解，获得了更稳健的位置估计，但未考虑锚点位置误差。本文首先引入锚点位置误差作为参数，重新建立TDOA定位模型，在此基础上提出基于凸优化的迭代定位算法，并通过仿真验证了算法性能。
1 TDOA定位模型
1.1 双曲线模型
TDOA定位双曲线模型包括多个坐标已知的定位锚点BS和一个待定位目标MS，如图1所示。
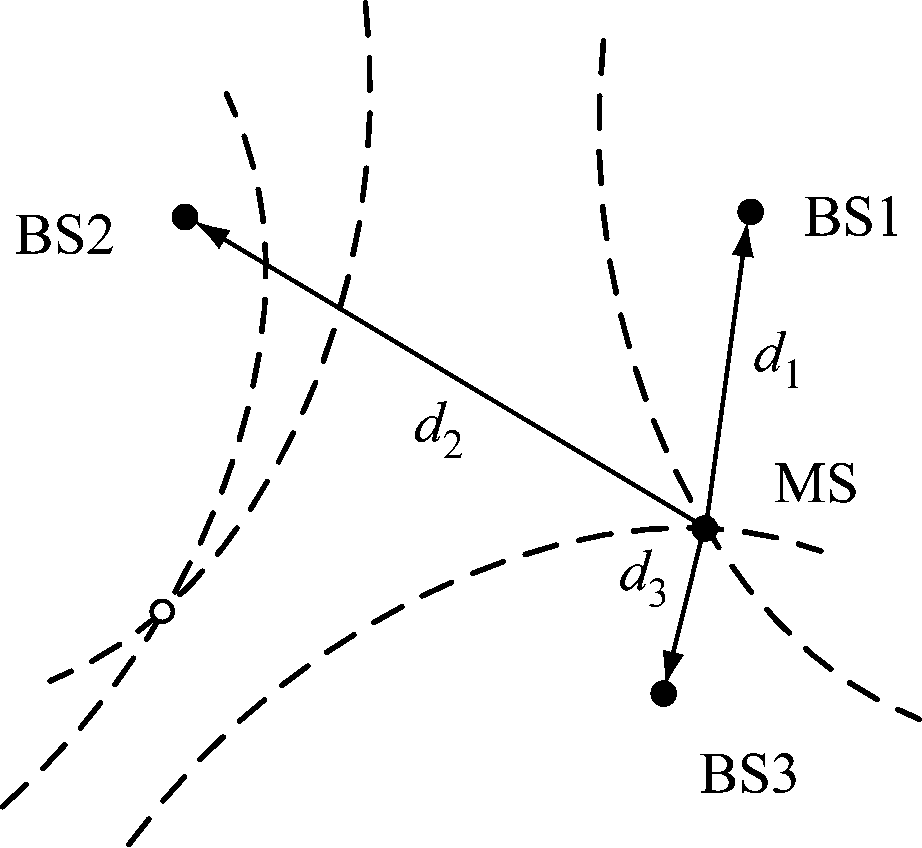
图1 TDOA定位双曲线模型
Fig.1 TDOA positioning hyperbolic model
待定位目标发射UWB信号，各锚点接收信号的同时记录相应的信号到达时间；选取一个锚点作为参考锚点，计算信号到达其他锚点与到达参考锚点的时间差，与信号传播速度相乘得到相应的距离差；通过该距离差得到锚点与待定位目标之间的位置关系，通过多组距离差可建立表征位置关系的方程组，从而实现定位。
根据几何关系，双曲线上任意一点到其两焦点距离差的绝对值为恒定值。因此以选定的两锚点为焦点作双曲线，则待定位目标处于该双曲线上。通过多组TDOA值可绘制多条不同的双曲线，不同双曲线之间的交点处即为目标的估计位置[12]。
1.2 数学模型
假设在三维空间布置N个锚点，第i个锚点的坐标为si(xi,yi,zi),i=1,2,…,N，待定位目标的坐标为u(x,y,z)。记待定位目标到第i个锚点的距离为di，即
取第1个锚点为参考锚点，则距离差可表示为
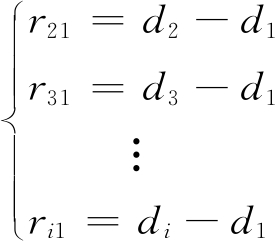
(1)
式中:ri1为TDOA测量值;
表示l2范数)。
由于测量值存在误差，将式(1)改写为向量的形式:
i=2,3,…,N
(2)
式中ni1为第i次TDOA测量噪声。
TDOA定位问题即转换为式(2)如何稳健求解问题[13-14]。
2 TDOA改进算法
2.1 问题建模
首先作如下设定：第i个锚点的真实坐标为
上标“o”表示相应变量的真实值)，含噪声测量值为si=[xi yi zi]T；待定位目标的真实位置坐标为uo=[xo yo zo]T，估计位置坐标为u=[x y z]T；定义
点位置误差Δβ=s-so，Δβ为0均值的高斯随机变量，协方差矩阵Qβ=E(ΔβΔβT)，E()表示数学期望；式(2)中ni1服从0均值的高斯分布，Δα=n=[n21,n31,…,nN1]T，Qα=E(ΔαΔαT)。
对式(2)进行最小二乘处理，即最小化测量误差为
(3)
式(3)未包含锚点位置误差，考虑锚点位置误差，引入加权矩阵W[15]，进行加权最小二乘求解，W包含TDOA测量误差及锚点位置误差。将式(3)改写成矩阵形式：
(4)
W=BQαBT+GQβGT
(5)
式中：r=[r21,r31,…,rN1]T；A=[-1m-1Im-1]，1m表示所有元素均为1的向量，Im为m×m的单位矩阵；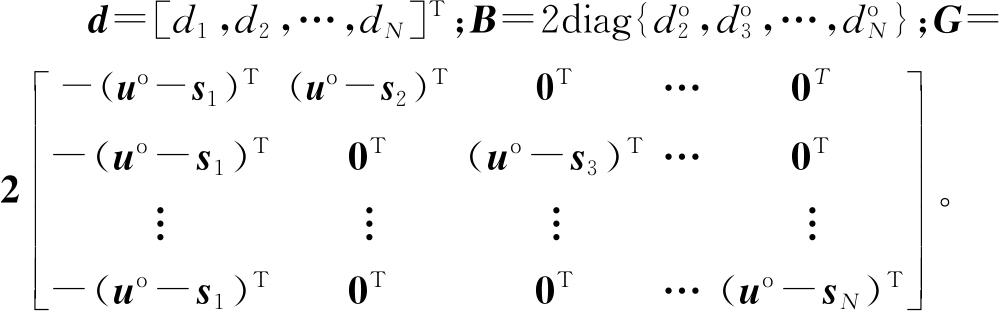
2.2 定位算法
式(4)是一个非凸最大似然估计问题，求解十分困难[16-18]。本文采用SDP解决方法，将非凸最大似然估计问题松弛为凸问题。TDOA改进算法步骤：① 将非凸目标函数转换成凸函数形式。② 将非凸约束函数松弛为与原始约束紧相关的凸约束。③ 对转换后的凸问题进行求解。
2.2.1 目标函数处理
将式(4)展开，并忽略常数项，得到等价的凸函数形式：
tr(ATW-1AD)-2dT(ATW-1r)
(6)
式中：tr()表示矩阵的迹；D=ddT。
式(6)是关于D和d的线性函数，是凸函数。
2.2.2 约束函数处理
对非凸约束函数进行松弛处理，得到与原始约束紧相关的凸约束。令y=uTu，则约束函数
可表示为
(7)
利用柯西-施瓦茨(Cauchy-Schwartz)不等式[19]处理式(7)可得
(8)
对于另外2个非凸约束D=ddT和y=uTu，利用半正定松弛方法进行松弛处理，得到
表示D-ddT是半正定矩阵)和
其线性矩阵不等式形式为
(9)
为了提高定位精度，采用一种常用的凸优化处理方法[20]，给目标函数增加一个惩罚项ηtr(D)，其中惩罚因子η>0。二阶锥(Second-Order Cone, SOC)约束[21]可表示为
(10)
2.2.3 凸问题求解
式(4)这个原始的非凸最大似然估计问题已转换为凸问题，对该凸问题可利用Matlab中的CVX工具箱[22]求解。SDP算法如下：
s.t.
(11)
惩罚因子η定义如下：
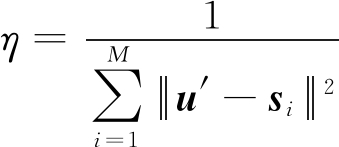
(12)
式中u′为不含惩罚项时定位目标的初始估计值。
通过迭代方法不断更新惩罚因子η，以达到更高的定位精度。基于凸优化的迭代算法的输入参数为TDOA测量值ri1、锚点位置坐标si、TDOA测量值噪声协方差矩阵Qα、锚点位置测量值噪声协方差矩阵Qβ、迭代次数L；输出量为待定位目标位置坐标
算法具体步骤如下：① 求解不含惩罚项和SOC约束的式(11)，利用估计值u′计算式(12)，得到η。② 将η代入式(11)中，求解该SDP问题，得到位置坐标初始估计值
③ 利用
更新η。④ 求解式(11)，得到新的坐标估计值⑤ 利用
更新η。⑥ 达到迭代次数前，重复执行步骤④-⑤。
3 仿真结果及分析
3.1 仿真环境搭建
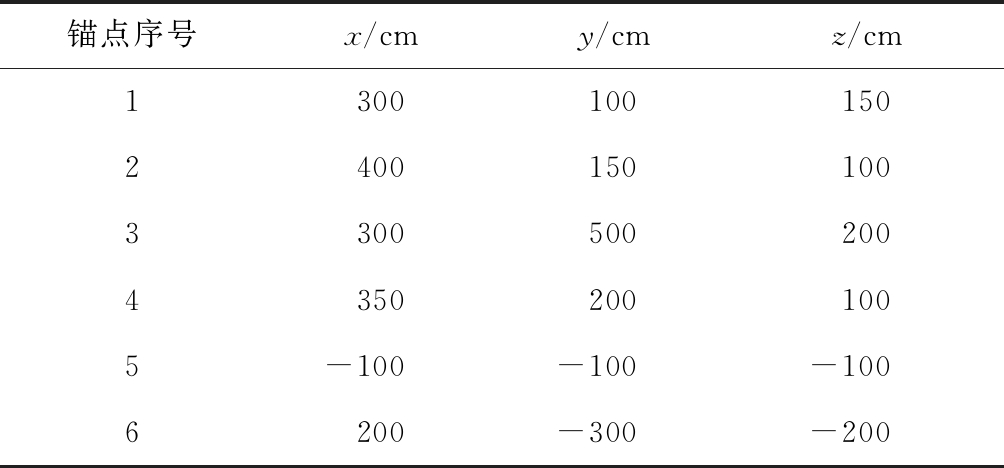
在三维空间中设置6个锚点，锚点坐标见表1。设TDOA测量值噪声和锚点位置噪声服从独立的均值为0的高斯分布，方差分别为
和
噪声协方差矩阵分别为
和
其中Σ是对角线元素为1、其余元素为0.5的方阵；算法仿真迭代次数L=5。在CVX工具箱中，设置求解器为“SeDuMi”，精度为“best”。
表1 锚点位置坐标
Table 1 Anchor position coordinates
3.2 仿真结果分析
采用均方误差E作为算法的性能评估指标，将本文提出算法与2种常用代数求解算法(TSWLS[10]，改进 TSWLS[11])及克拉美罗下限(CRLB)进行对比。CRLB是所有无偏参数估计器的下界，适用于平稳的高斯信号估计。因此,将本文算法定位结果与CRLB进行对比，以体现算法的定位性能。
考虑近距离场景，假定目标真实坐标为(285,325,275)，研究算法定位精度与锚点位置误差之间的关系，结果如图2所示。
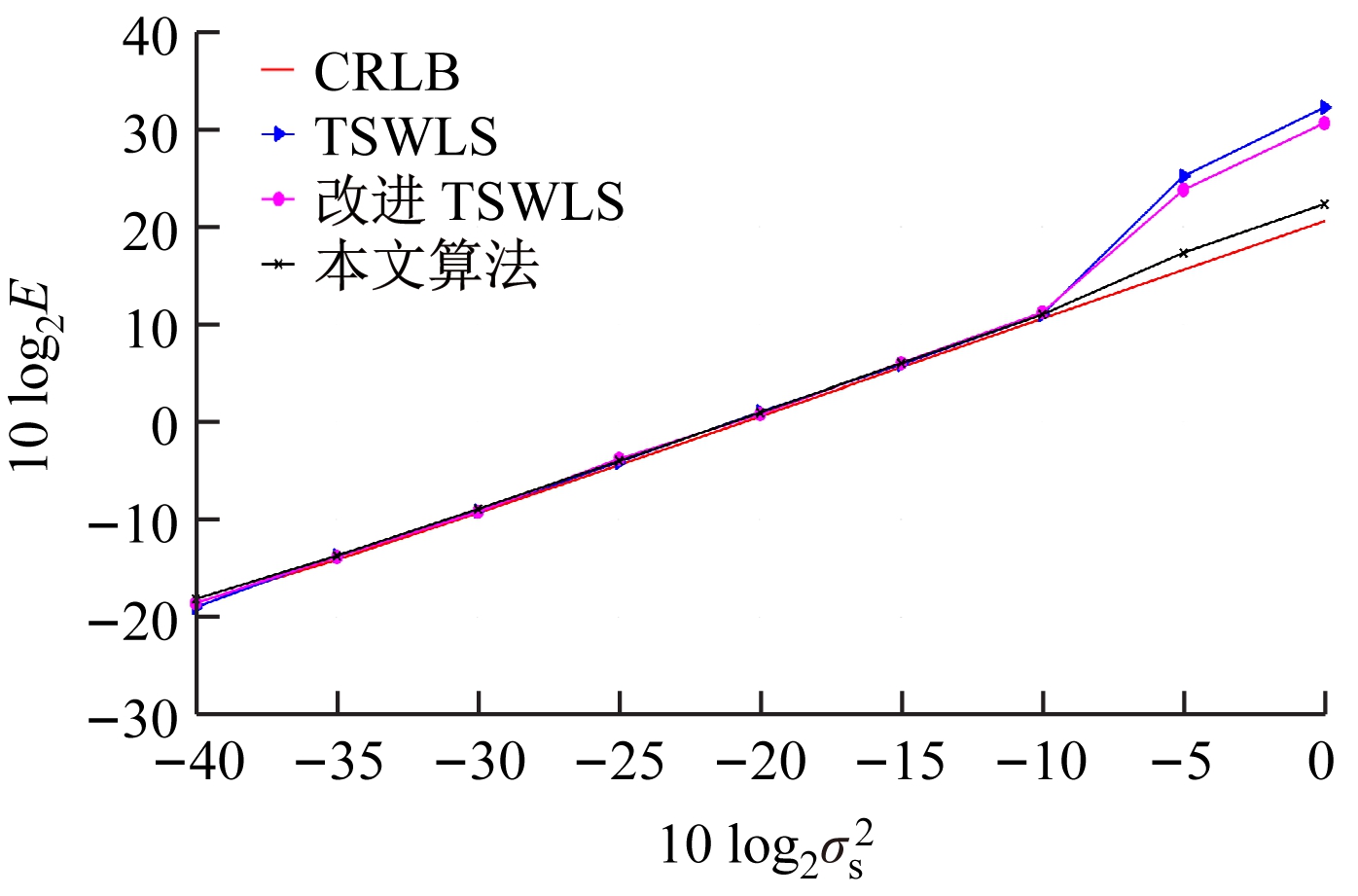
图2 近距离场景下存在锚点误差时不同算法均方误差比较
Fig.2 Comparison of MSE of different algorithms when there is anchor error in close scene
仿真结果表明,随着锚点位置误差增大，算法性能逐渐下降；TSWLS、改进 TSWLS存在明显的阈值效应，当基站位置误差较小时，算法可达CRLB，但当噪声增大到一定程度时，算法性能下降严重；而本文提出的SDP算法可以有效逼近CRLB，当锚点位置误差为1 cm时，算法定位精度可达到5 cm。
考虑远距离场景，假定目标真实坐标为(2 000，2 500，3 000)，研究算法定位精度与锚点位置误差之间的关系，结果如图3所示。从仿真结果可看出，相比于近距离场景，本文算法性能有所下降，随着锚点位置误差增大，均方误差相对于CRLB有一定的偏离，但性能仍优于其他2种算法。
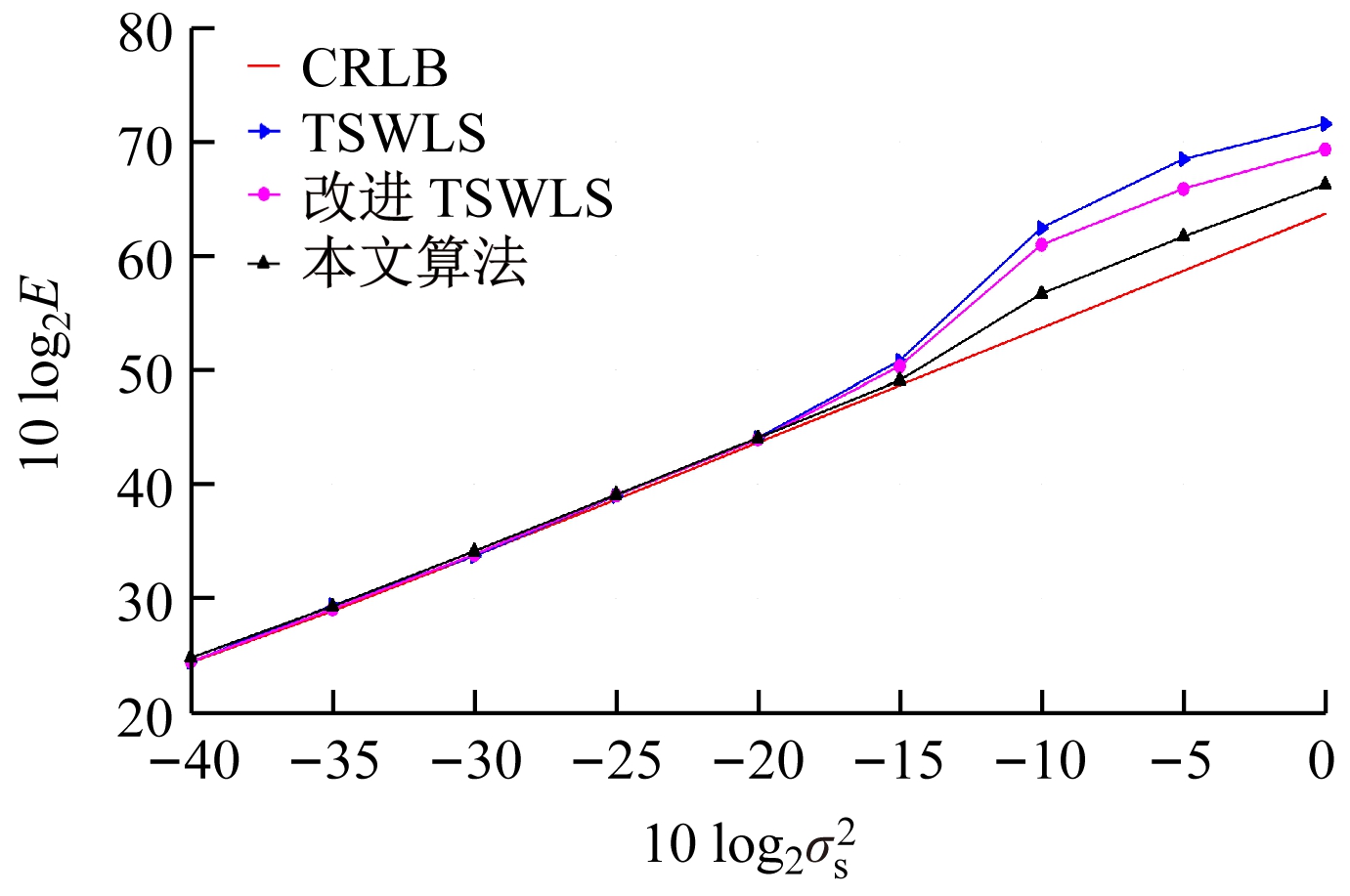
图3 远距离场景下存在锚点误差时不同算法均方误差比较
Fig.3 Comparison of MSE of different algorithms when there is anchor error in long distance scene
在大规模场景中，应采用协同定位的思想，布置大量基站。当目标处于不同区域时，仅利用距离目标最近的几个基站代入SDP算法进行定位，可确保每次定位的区域范围不会过大，避免定位精度下降。
4 结语
介绍了井下TDOA定位双曲线模型和数学模型，考虑锚点位置误差，对模型进行改进，并提出基于凸优化的迭代定位算法，详细介绍了算法的推导及实现过程。仿真结果表明，当锚点位置误差为1 cm时，算法定位精度可达到5 cm；即使在测量噪声较大时，该算法仍可有效逼近CRLB，优于现有的TSWLS、改进TSWLS算法。
参考文献（Ｒｅｆｅｒｅｎｃｅｓ）：
[1] 田成金.薄煤层自动化工作面关键技术现状与展望[J].煤炭科学技术,2011,39(8):83-86.
TIAN Chengjin.Status and outlook of key technology for automation coal mining face in thin seam[J].Coal Science and Technology,2011,39(8):83-86.
[2] 赵锐,钟榜,朱祖礼,等.室内定位技术及应用综述[J].电子科技,2014,27(3):154-157.
ZHAO Rui,ZHONG Bang,ZHU Zuli,et al.Overview of indoor localization techniques and applications[J].Electronic Science and Technology,2014,27(3):154-157.
[3] 孙继平.煤矿信息化自动化新技术与发展[J].煤炭科学技术,2016,44(1):19-23.
SUN Jiping.New technology and development of mine informatization and automation[J].Coal Science and Technology,2016,44(1):19-23.
[4] 孙哲星.基于时间测距的矿井人员定位方法研究[J].工矿自动化,2018,44(4):30-33.
SUN Zhexing.Research on mine personnel positioning method based on time range[J].Industry and Mine Automation,2018,44(4):30-33.
[5] BOCQUET M, LOYEZ C, BENLARBI-DELAI A. Using enhanced-TDOA measurement for indoor positioning[J]. IEEE Microwave & Wireless Components Letters, 2005,15(10):612-614.
[6] WEI H W, PENG R, WAN Q, et al. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2010,58(3):1677-1688.
[7] CHAN Y T, HO K C. Asimple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994,42(2): 1905-1915.
[8] HO K C, LU X, KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[J]. IEEE Transactions on Signal Processing, 2007,55(2):684-696.
[9] YANG L, FU G, LE Y, et al. An improved algebraic solution for TDOA-based localization with sensor position errors[J]. IEEE Communications Letters, 2015,19(12):2218-2221.
[10] GANG W, LI Y, ANSARI N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Vehicular Technology, 2013,62(2):853-862.
[11] ZOU Yanbin,LIU Huaping, WAN Qun. An iterative method for moving target localization using TDOA and FDOA measurements[J].IEEE Access,2016,4:2746-2754.
[12] HO K C, KOVAVISARUCH L, PARIKH H. Source localization using TDOA with erroneous receiver positions[C]//International Symposium on Circuits & Systems, 2004.
[13] ROSIC M, SIMIE M, LUKIC P. TDOA approach for target localization based on improved genetic algorithm[C]//Telecommunications Forum, 2017.
[14] GANG W, SO M C, LI Y. Robust convex approximation methods for TDOA-based localization under NLOS conditions[J]. IEEE Transactions on Signal Processing, 2016,64(13):3281-3296.
[15] SENGIJPTA S K. Fundamentals of statistical signal processing:estimation theory[J]. Control Engineering Practice, 1994, 37(4):465-466.
[16] SUN M, HO K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59(7):3434-3440.
[17] YU H, HUANG G, GAO J. Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J]. Iet Radar Sonar & Navigation, 2012,6(9):891-899.
[18] XU Enyang, DING Zhi, DASGUPTA S. Source localization in wireless sensor networks from signal time-of-arrival measurements[J]. IEEE Transactions on Signal Processing, 2011,59(6):2887-2897.
[19] ZOU Y, WAN Q. Asynchronous time-of-arrival-based source localization with sensor position uncertainties[J]. IEEE Communications Letters, 2016,20(9):1.
[20] WEI W, GANG W, FAN Z, et al. Second-order cone relaxation for TDOA-based localization under mixed LOS/NLOS conditions[J]. IEEE Signal Processing Letters, 2016,23(12):1872-1876.
[21] STEPHEN BOYD L V. Convex optimization[J]. IEEE Transactions on Automatic Control, 2006,51(11):1859.