0 引言
爆破开挖产生的扰动会直接影响地下空间的安全和稳定[1]。研究显示，对于露天爆破或浅埋深地下爆破，岩体受到的扰动仅由爆炸荷载作用引起；对于深埋深、高应力环境下岩体，钻爆开挖给围岩造成的扰动则是由爆炸荷载和岩体开挖瞬间卸荷共同作用引起[2]，其中，爆破振动是关键，它受岩体特性、地质状况、炸药类型、钻孔参数、装药结构、装药量、起爆方法和爆心距等因素的影响[3-4]。当前，国内外研究者对爆破扰动下开挖空间围岩的稳定性进行了研究，文献[5]以巷道表面位移或塑性区范围作为围岩稳定性判定指标；文献[6]基于一维应力波理论，结合岩石拉伸极限应变推算爆破的临界振动速度；文献[7]提出通过将岩体动力强度与开挖空间所受动静应力之和相平衡，来确定爆破振动影响下无支护空间出现不同破坏时的围岩临界振动速度。现有研究大多为定性研究，较少涉及定量的理论研究，围岩受爆破扰动下的稳定性判定尚无统一的方法[8]。
本文基于弹性力学建立圆形巷道及其围岩等效力学模型，研究爆破扰动下围岩体发生临界破坏的深度及其影响因素的变化规律，获得了使巷道围岩不发生剪切破坏的临界爆破振动速度，可为工程施工提供理论参考。
1 巷道及其围岩力学分析
假设巷道断面为圆形，将巷道及其围岩等效成圆筒，如图1所示，圆筒内半径为r，外半径为R，内压力q为爆破扰动力。由于现场普通巷道常采用一次瞬间起爆法，巷道断面各炮孔起爆产生的冲击波共同作用在围岩内壁上的压力可等效成一个集中药包爆炸时对内壁产生的压力，故根据文献[9]可得q=γcv，其中γ为介质密度，c为爆破振动速度，v为波速。c可用经验公式计算：
其中k为岩石普氏系数；Q为一次起爆最大药量;R0为装药中心至围岩内壁的距离;α为衰减系数。假设圆筒无外压力，显然，围岩内任意一点处的应力分布应当是轴对称的。因此，应力分量表达式为
(1)
(2)
τφρ=0
(3)
式中：σρ为径向应力；σφ为环向应力；ρ为围岩内任意一点至巷道圆心的距离；A,B,D为待定系数；τφρ为切向应力。
图1 巷道及其围岩等效力学模型
Fig.1 Equivalent mechanics model of roadway and its surrounding rock
由内外边界条件(σρ)ρ=r=-q和(σρ)ρ=R=0可得
(4)
(5)
由环向位移
的单值条件可知：
B=0
(6)
式中：φ为围岩内任意一点的极角；E为围岩体弹性模量；H，I，K为常系数。
联立式(4)—式 (6)可得
将A和2D代入应力分量表达式可得围岩受均布压力时的应力：
(7)
(8)
考虑到爆破扰动是在巷道表面一定范围内，故令R→∞，则式(7)和式(8)可简化为
(9)
(10)
假设围岩内一点的单元体S在径向应力和环向应力作用下会发生剪切破坏，破坏遵循莫尔库伦准则，则在应力作用下单元体发生临界破坏时的莫尔应力圆将和围岩体的莫尔库伦曲线相切，如图2所示。
图2 莫尔应力圆与剪切破坏准则曲线
Fig.2 Mohr stress circle and shear failure criterion curve
从图2中的几何关系可得
(11)
式中：C为围岩体的黏聚力;φ为围岩体的内摩擦角。
将式(9)、式(10)代入式(11)，化简可得围岩内的点在爆破扰动作用下即将发生破坏(临界破坏)时满足的关系：
(12)
式中γ为围岩密度。
由于力学模型是轴对称的，故各个临界破坏点的连线是一个与巷道有相同圆心的圆形。
以巷道表面为起点，围岩受爆破扰动时的临界破坏深度d可表示为
(13)
通过一个算例来说明式(13)的应用。用钻爆法在某煤层中开掘巷道，设巷道的开挖半径为2 m，煤层的黏聚力及内摩擦角分别为1.2 MPa和30°，围岩密度为2 300 kg/m3，爆破振动速度为0.24 m/s，振动引起的应力波传播速度为3 600 m/s，则围岩的临界破坏深度为
m,即在围岩内0.76 m处将会发生剪切破坏。这说明爆破扰动下巷道围岩的破坏并非最先发生在巷道表面，而是在围岩内某个位置，这是由扰动力性质、围岩应力分布和围岩体力学性质综合决定的。在这些决定因素中，爆破振动速度可以通过一次起爆的最大装药量来控制。因此，从理论上讲，通过控制爆破振动速度可以达到防止围岩破坏的目的，即当临界破坏深度d=0时，使围岩不发生破坏的爆破振动速度
即临界爆破振动速度，在本例中，
m/s。得到c0后，即可根据
求得围岩不发生破坏时的装药量。
2 影响围岩临界破坏深度的因素分析
从上述分析可以看出，爆破扰动下的围岩临界破坏深度主要受巷道开挖半径、围岩黏聚力和内摩擦角、围岩密度、爆破振动速度等因素影响。基于正交试验[10]分析这些因素对破坏深度的影响规律。正交试验指标定为临界破坏深度，其值由式(13)计算得到。试验方案选取4因素3水平，各因素及其水平依次为：巷道开挖半径为2.0，2.5，3.0 m；爆破振动速度为0.36，0.48，0.60 m/s；黏聚力为1.2，1.7，2.2 MPa；内摩擦角为25°，28°，31°。围岩密度和应力波波速分别取2 300 kg/m3和3 600 m/s。试验中，用mjk表示第j列因素k水平所对应的试验指标和，通过其平均值mk的大小可以判断第j列因素对试验指标的影响规律。试验结果见表1,可见,各影响因素的重要性程度从大到小依次为黏聚力、爆破振动速度、巷道开挖半径、内摩擦角。
表1 围岩临界破坏深度影响因素试验结果
Table 1 Experimental results of influence factors of critical failure depth of surrounding rock
各影响因素与围岩临界破坏深度的关系如图3所示。
从图3可以看出：
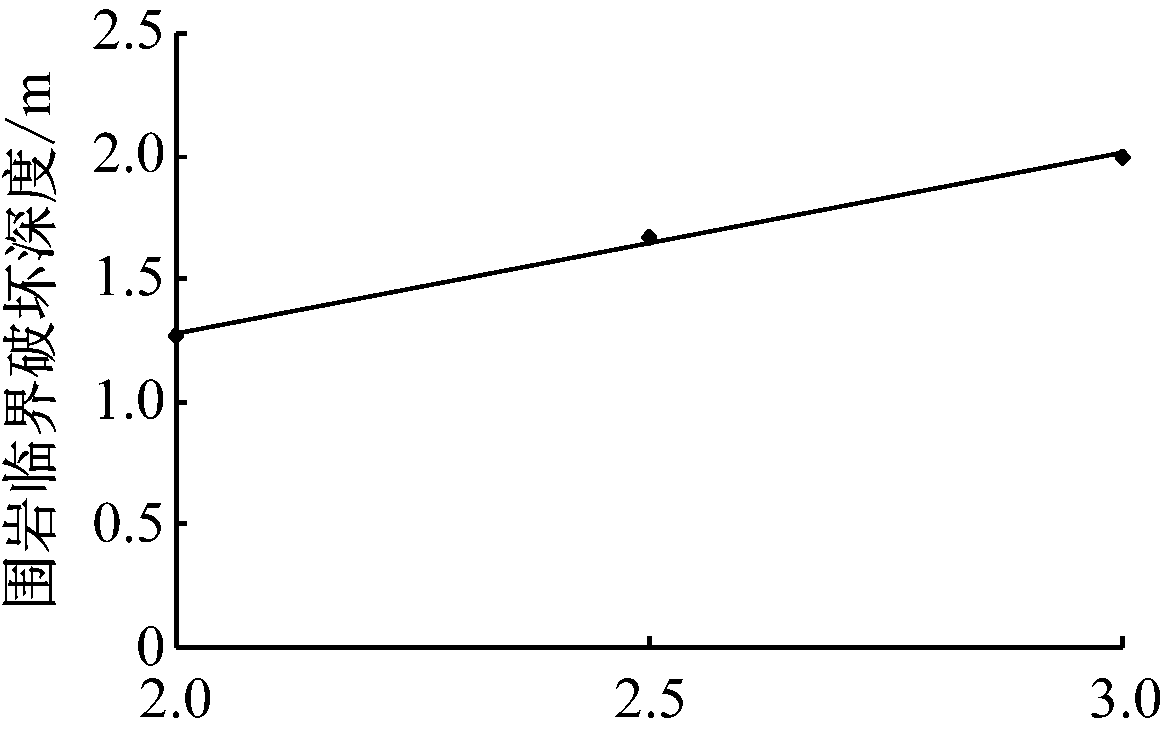
(1) 随着巷道开挖半径r的增加，围岩临界破坏深度d呈线性规律增大,d=0.365r+0.916 7。开挖半径每增加1 m，临界破坏深度就相应地向围岩深部扩大0.365 m，破坏深度约为开挖半径的67%。说明开挖巷道的断面越大，越应关注深部围岩的稳定情况，特别是要及时加强围岩内深度为开挖半径67%处的支护强度，以免因开挖扰动造成此处围岩失稳。
(2) 随着爆破振动速度c的增加，围岩临界破坏深度d呈对数规律增大：
增大的过程中，d增量逐渐减小，可见，临界破坏深度并不随爆破强度的增大而同比例增加。由前面的理论推导可以发现，爆破振动对围岩的影响会随振动产生的应力波传递到围岩深部，所以在施工过程中，仍要考虑在满足爆破效果的前提下尽可能优化爆破参数和起爆方法，以降低爆破振动，减小破坏深度，确保该深度不超过现有技术水平下的支护深度。
(3) 黏聚力C是岩体固有的力学特性参数，反映了围岩体的抗剪切破坏能力。C越大，围岩抗剪强度越大，围岩临界破坏深度d越小，两者的关系为d=3.672 5exp(-0.431 4C)。黏聚力对围岩临界破坏深度有显著的影响，C每增大1 MPa，d就相应地减小2.37 m。可见，提高围岩体的黏聚力对保持围岩稳定至关重要，对于破碎松散岩体的施工，宜先采取超前支护加工作面预注浆的方式来加固围岩，以提高其黏聚力，之后再进行爆破开挖。
巷道开挖半径/m
(a) 巷道开挖半径的影响
爆破振动速度/(m·s-1)
(b) 爆破振动速度的影响
黏聚力/MPa
(c) 黏聚力的影响
内摩擦角/(°)
(d) 内摩擦角的影响
图3 各影响因素与围岩临界破坏深度的关系
Fig.3 Relation between influence factors and critical failure depth of surrounding rock
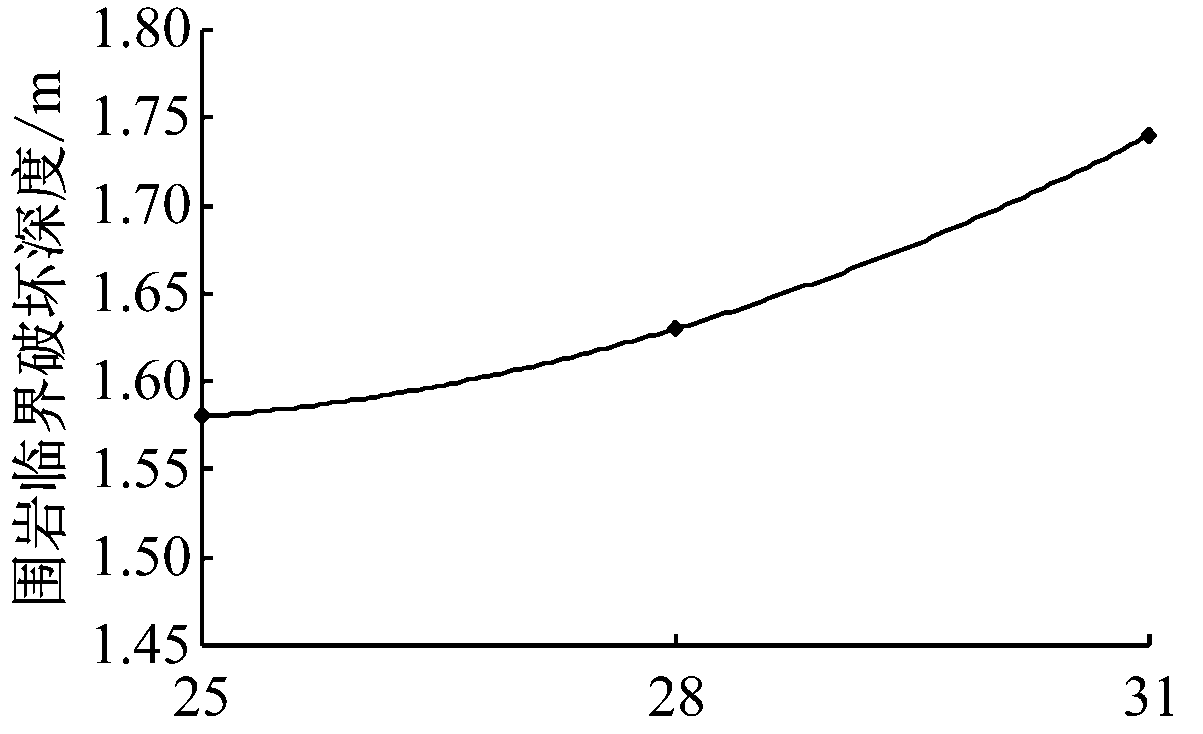
(4) 内摩擦角φ与围岩临界破坏深度d呈二次多项式关系,d=0.03φ2-0.04φ+1.59。在试验参数变化范围内，d随φ增大而增大，但这种增幅非常小，φ每增大1°，d只增大26.7 mm，说明φ的变化对d的影响十分有限。因此，在围岩地质资料不足的研究或施工中，结合岩体内摩擦角的取值范围，建议使用φ=28°来计算d值。
(5) 由试验结果可知，巷道开挖半径、爆破振动速度、围岩黏聚力和内摩擦角的极差分别为0.73，1.14，1.37和0.16，显示这些因素对临界破坏深度影响的重要性程度从大到小依次为C,c,r,φ，而且C与c的试验极差明显比其他因素的极差大，两者的影响程度分别占到40.29%和33.53%，说明围岩黏聚力和爆破振动速度是影响围岩破坏深度的2个最显著因素。因此，采用钻爆法开挖巷道时，围岩强度和爆破强度是必须认真考虑的两大因素。
3 结论
(1) 基于弹性力学理论，得到巷道围岩受爆破扰动时的临界破坏深度，分析得出临界破坏深度与围岩体黏聚力及内摩擦角、岩体密度、爆破振动速度、应力波波速和巷道开挖半径有关。
(2) 通过力学分析，得到不使巷道围岩发生破坏的临界爆破振动速度。
(3) 分析了临界破坏深度随巷道开挖半径、爆破振动速度、围岩体黏聚力及内摩擦角的变化规律。结果表明，围岩体黏聚力和爆破振动速度是影响围岩破坏深度的2个最显著的影响因素。
参考文献(References)：
[1] 徐芝纶.弹性力学简明教程[M].3版.北京:高等教育出版社,2002.
[2] 戴俊.岩石动力学特性与爆破理论[M].2版.北京:冶金工业出版社,2013.
[3] 刘国华,王振宇.爆破荷载作用下隧道的动态响应与抗爆分析[J].浙江大学学报(工学版) ,2004,38(2):204-209.
LIU Guohua,WANG Zhenyu.Dynamic response and blast-resistance analysis of a tunnel subjected to blast loading[J].Journal of Zhejiang University(Engineering Science),2004,38(2):204-209.
[4] 刘晶波,李彬.Rayleigh波作用下地下结构的动力反应分析[J].工程力学,2006,23(10):132-135.
LIU Jingbo,LI Bin.Dynamic response analysis of underground structures during propagation of Rayleigh waves[J].Engineering Mechanics,2006,23(10):132-135.
[5] 李化敏,胡劲松,李效甫.深井巷道矿压与支护问题探讨[J].焦作矿业学院学报,1994,13(3):22-26.
LI Huamin,HU Jinsong,LI Xiaofu.The study on ground pressure and support problems in roadways of deep coal mines[J].Journal of Jiaozuo Mining Institute,1994,13(3):22-26.
[6] 杨科之,杨秀敏.坑道内化爆冲击波的传播规律[J].爆炸与冲击,2003,23(1):37-40.
YANG Kezhi,YANG Xiumin.Shock waves propagation inside tunnels[J].Explosion and Shock Waves,2003,23(1):37-40.
[7] 孔德森,孟庆辉,张伟伟,等.爆炸荷载作用下地铁隧道的冲击反应研究[J].振动与冲击,2012,31(12):68-72.
KONG Desen,MENG Qinghui,ZHANG Weiwei,et al.Shock responses of a metro tunnel subjected to explosive loads[J].Journal of Vibration and Shock,2012,31(12):68-72.
[8] 钱七虎.岩石爆炸动力学的若干进展[J].岩石力学与工程学报,2009,28(10):1945-1968.
QIAN Qihu.Some advances in rock blasting dynamics[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1945-1968.
[9] 吴亮,李凤,卢文波,等.爆破扰动下邻近层状围岩隧道的稳定性与振速阈值[J].爆炸与冲击,2017,37(2):208-214.
WU Liang,LI Feng,LU Wenbo,et al.Vibration velocity threshold of a tunnel adjacent to surrounding layered rocks under blasting load[J].Explosion and Shock Waves,2017,37(2): 208-214.
[10] 卫志强,任智敏,王树祥.大断面回采巷道稳定性数值模拟研究[J].爆破,2012,29(3):42-44.
WEI Zhiqiang,REN Zhimin,WANG Shuxiang.Numerical simulation of stability of large section mining roadway[J].Blasting,2012,29(3):42-44.