0 引言
轴承是旋转机械中支撑和传递动力的关键部件,也是最容易出现故障的部件。据统计,大约有30%的旋转机械故障是轴承故障引起的,因此,轴承的健康状况直接影响整台设备的性能,故对轴承状态进行监测、及时发现并识别轴承故障具有重要的实际意义。
当滚动轴承处于故障早期阶段时,由于受环境噪声、振动传递过程的干扰及衰减、多振动源激励及其响应相互耦合、气隙、动载荷等诸多因素影响,其振动信号具有复杂的特征。对振动信号进行去噪处理后,能更好地提高信噪比,使后续处理得到更为准确的结果。经验模态分解(Empirical Mode Decomposition,EMD)方法克服了传统包络分析需要预先确定滤波器参数的难题[1],因此,基于EMD的包络分析法在滚动轴承故障诊断中得到了广泛应用[2-3]。该方法会产生模态混叠现象,目前大部分文献都是选取前几阶本征模态函数(Intrinsic Mode Function,IMF)分量作为有效分量,把其他IMF分量作为干扰和噪声去除,当原始信号的信噪比较低时,很难有效准确地提取故障特征[4-5]。
集合经验模态分解(Ensemble EMD,EEMD)算法在振动信号中多次加入白噪声并进行EMD分解,然后对多次分解得到的IMF分量求平均值,这样既获得了准确的 IMF分量,又消除了白噪声的影响,从而有效克服了EMD算法分解过程中因信号不连续产生的模式混叠问题[6]。经EEMD分解的IMF分量更加独立,有利于后续的IMF选取。而直接选取前几阶IMF分量的方法会使得其他有效IMF分量丢失。为了将含有丰富故障信息的IMF分量选择出来,减少或去除虚假分量及噪声分量,本文将相关系数准则、J散度准则和峭度准则相融合进行IMF分量选择,提出了基于多准则融合的滚动轴承振动信号消噪方法。因为EEMD算法本身较为成熟,本文不作具体介绍,而重点介绍如何基于多准则融合进行有效IMF分量的选择。
1 消噪方法流程
基于多准则融合的滚动轴承振动信号消噪方法流程如图1所示。首先采用EEMD方法对滚动轴承原始振动信号进行分解,得到一组IMF分量;然后计算各阶IMF分量与原始振动信号的相关系数、各阶IMF分量和原始振动信号包络谱的J散度、各阶IMF分量的峭度值;将相关系数准则、J散度准则、峭度准则进行融合,选取有效的IMF分量,并进行信号重构。
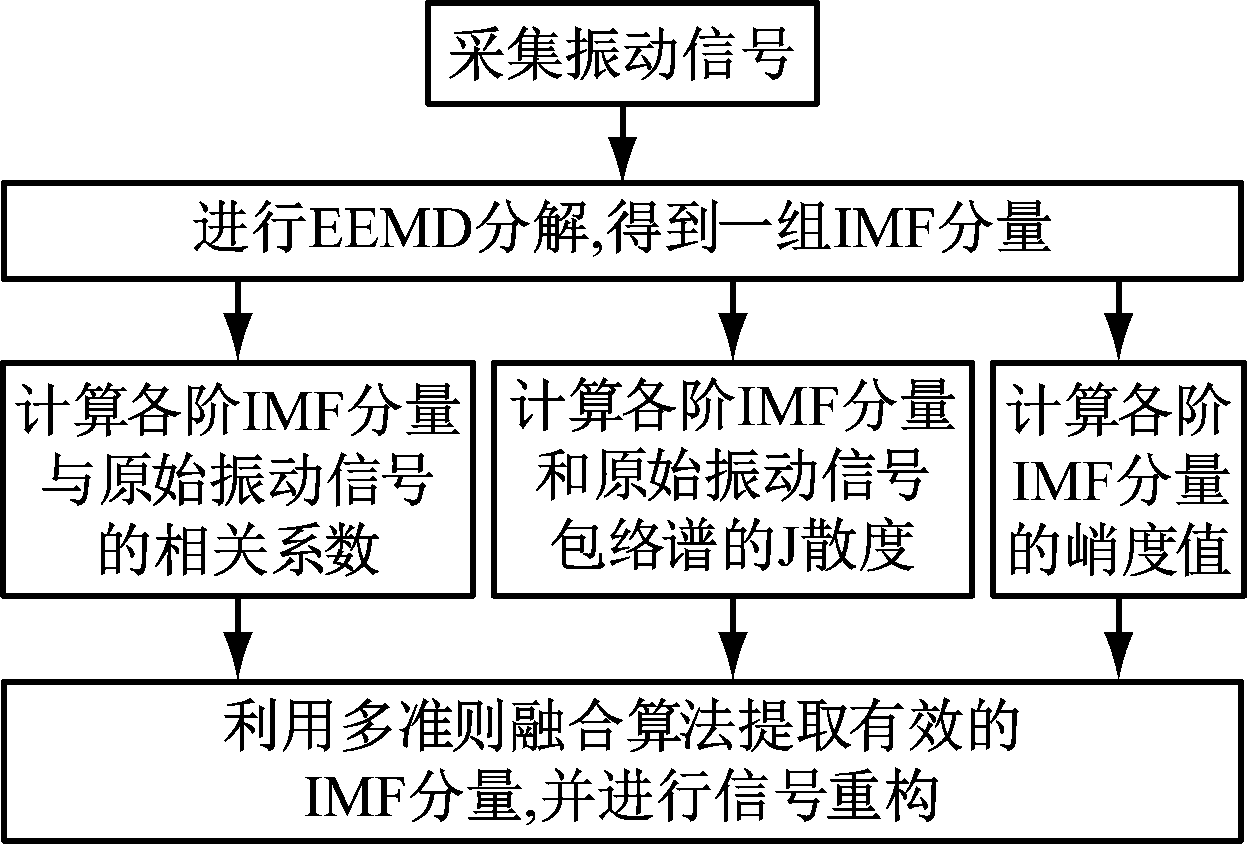
图1 基于多准则融合的滚动轴承振动信号消噪方法流程
Fig.1 Flow of denoising method of vibration signal of
rolling bearing based on multi-criteria fusion
2 多准则融合算法
多准则融合即分别根据相关系数准则、J散度准则、峭度准则选取有效IMF分量,将同时保留的IMF分量作为有效分量进行信号重构。相关系数准则和J散度准则分别从时域和包络域分析IMF分量与原始振动信号的相似程度,根据设定的阈值实现虚假IMF分量剔除。融合这2个准则能提高IMF分量选取的区分度,减小阈值边界附近的误判,有效抑制低频干扰。根据峭度准则可选出含有丰富故障信息的IMF分量,增强故障特征。因此,基于多准则融合的滚动轴承振动信号消噪方法能抑制低频干扰,突出高频共振成分。
2.1 相关系数准则
用式(1)计算原始振动信号与各阶IMF分量的相关系数:

(1)
式中:x(n)为原始振动信号序列;IMFi(n)为分解后的第i阶IMF序列,i为正整数,0<i<I,I为IMF分量个数。
真实的IMF分量与原始信号的相关系数较大,虚假的IMF分量与原始信号的相关系数较小,因此,可依据IMF分量与原始信号的相关系数的大小选取真实有效的IMF分量。具体方法如下:将IMF分量按相关系数从大到小的顺序排列,计算相邻相关系数的差值并找出差值最大的2个相关系数,将这2个相关系数对应的IMF分量及其之前的IMF 分量视为有效分量[7],即相关系数大于或等于这2个IMF分量的IMF分量均为有效分量。
2.2 J散度准则
用式(2)计算原始振动信号与各阶IMF分量的J散度:
(2)
式中:N为采样长度;fx为样本信号的幅值谱或包络谱;fIMFi为分解后的第i阶IMF分量的幅值谱或包络谱。
J散度是描述信号间谱距离的参数,可以反映2个信号间的相似程度,因此,可用J散度判断EEMD分解后的IMF分量与原始振动信号的相似程度。信号包络谱对轴承故障非常敏感,通过包络谱可以十分清晰地看到因故障冲击所形成的峰值,即在轴承故障的特征频率处会出现谱峰,且与频谱相比包络谱的谱线清晰简单。因此,可通过计算原始振动信号与其分解后的各阶IMF分量的包络谱的距离求出J散度。J散度值越大,表明IMF分量与原始振动信号的相似程度越大,反之则越小,同一信号的J散度值等于0。J散度值一般横跨几个数量级,根据仿真比较及经验,本文设定数量级1为剔除域,即J散度值大于1的IMF分量被视为无效分量,小于或等于1的IMF分量被视为有效分量[8]。
2.3 峭度准则
用式(3)计算各阶IMF分量的峭度:
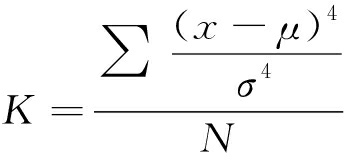
(3)
式中:μ为信号x的均值;δ为信号x的标准差。
峭度是描述波形尖峰度的一个无量纲参数,与轴承的转速、尺寸及载荷等参数没有关系,但它对轴承造成的冲击信号格外敏感。滚动轴承正常状态时的振动信号接近正态分布,其峭度值在3左右,出现局部故障后,由于故障引起的冲击成分使振动信号偏离正态分布,其峭度值明显增大。因此,EEMD 分解后IMF分量的峭度值越大,说明其含有的故障冲击成分越多,携带的故障信息越丰富。依次计算出各阶IMF分量的峭度值,保留峭度值较大的IMF分量,把其他阶的IMF分量作为噪声直接去除,即可滤除低频干扰,突出故障信息。
3 实验分析
3.1 实验装置及条件
轴承振动信号故障数据来源于美国 Western Reserve University 滚动轴承研究中心,滚动轴承实验装置如图2所示。为模拟滚动轴承早期微弱故障,通过放电加工技术在驱动端轴承外圈的3点钟方向及内圈加工了直径为0.017 78 cm的单点故障。通过安装在电动机壳体驱动端的加速度传感器采集轴承振动信号,采样频率为12 kHz。驱动端采用SKF6205深沟球轴承,其参数设置如下:滚道节径为3.904 cm,铜球直径为0.794 cm,铜球个数为9,接触角为0,采样频率为12 000 Hz,采样点数为8 192。由文献[9]中的理论公式可计算出滚动轴承内圈特征频率为157.76 Hz。

图2 滚动轴承实验装置
Fig.2 Experimental device of rolling bearing
3.2 滚动轴承内圈故障分析
设置电动机转速为1 748 r/min,在1 492 W负载下测试内圈故障数据,其时域波形及频谱如图3所示。
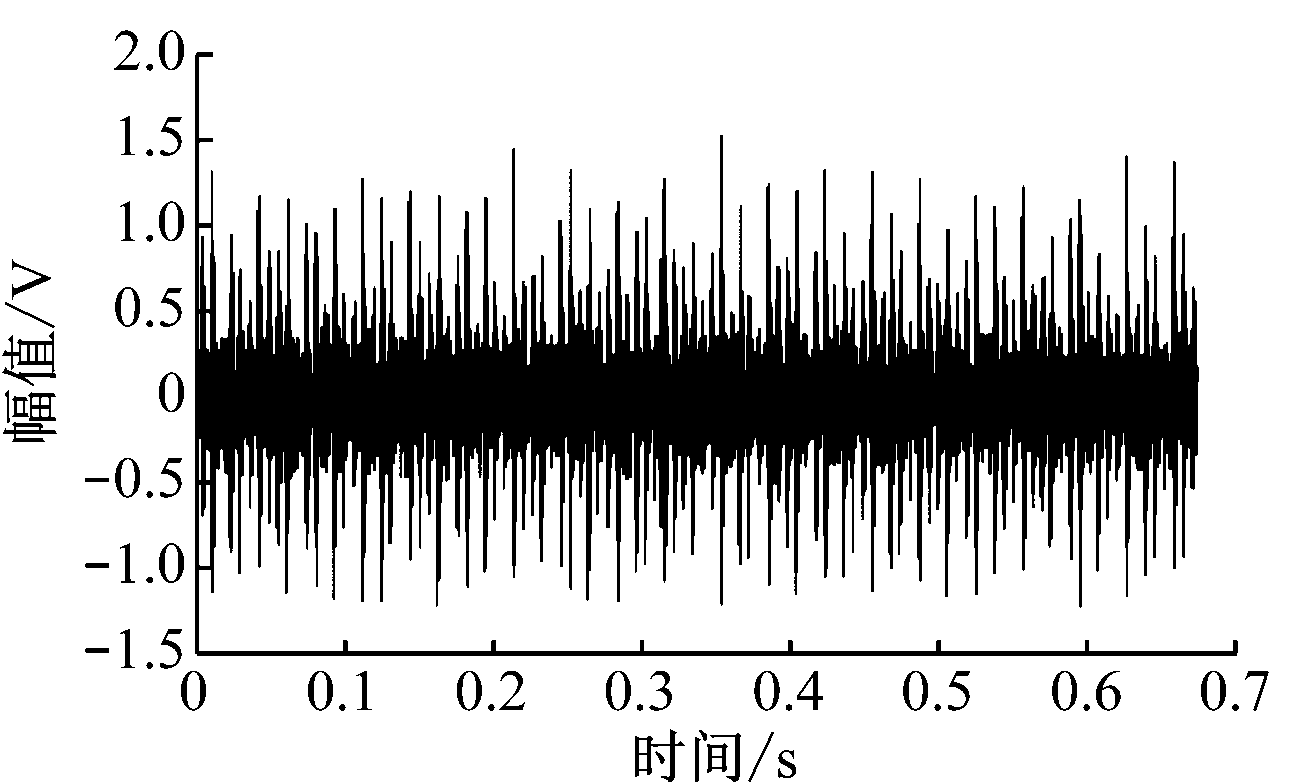
(a) 内圈故障时振动信号时域波形
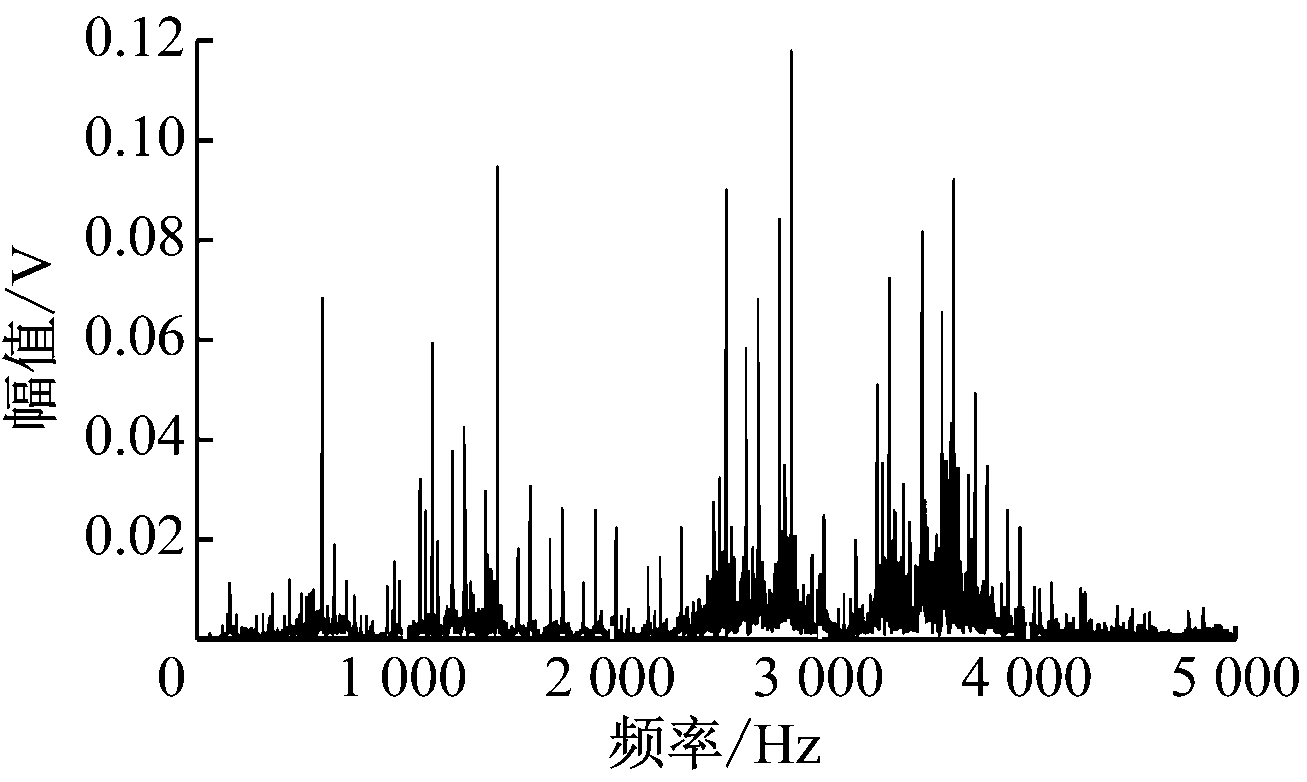
(b) 内圈故障时振动信号频谱
图3 内圈故障时振动信号时域波形及频谱
Fig.3 Time domain waveform and amplitude spectrum of
vibration signal of inner ring fault
从时域波形可以看出周期冲击成分,表明轴承出现了故障,但无法判断故障的类型。从频谱图中可以看出,在2 500~4 000 Hz之间存在高频共振区,但无法识别内圈故障特征信号。
内圈故障时原始振动信号包络谱及EEMD分解后的IMF1—IMF8的包络谱分别如图4、如图5所示。由图4可看出,包络谱中出现了转频(29.3 Hz)、二倍转频(58.59 Hz)、内圈故障特征频率(156.7 Hz)等谱线以外的若干波峰,不利于故障特征提取。
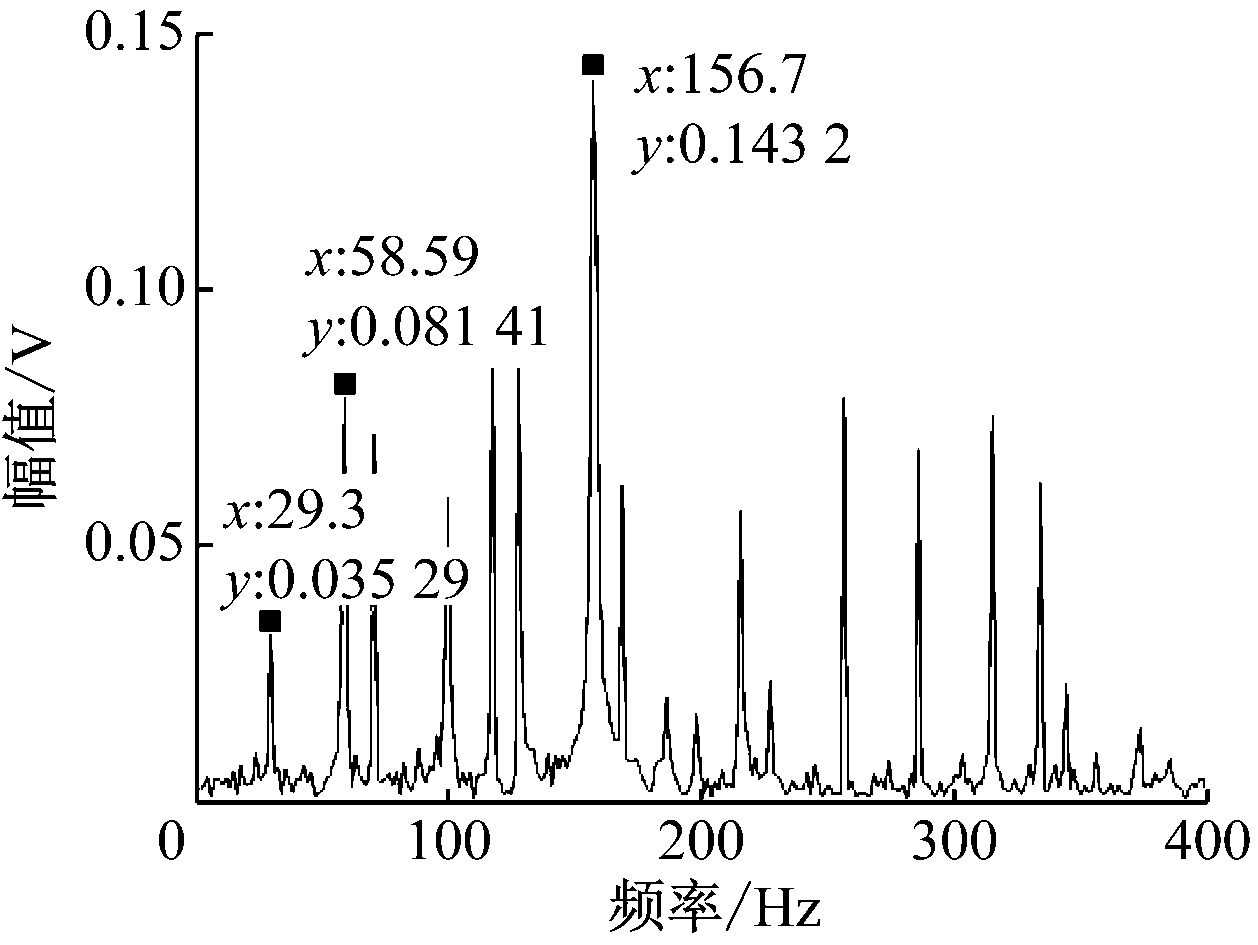
图4 内圈故障时原始振动信号包络谱
Fig.4 Envelope spectrum of original vibration
signal of inner ring fault


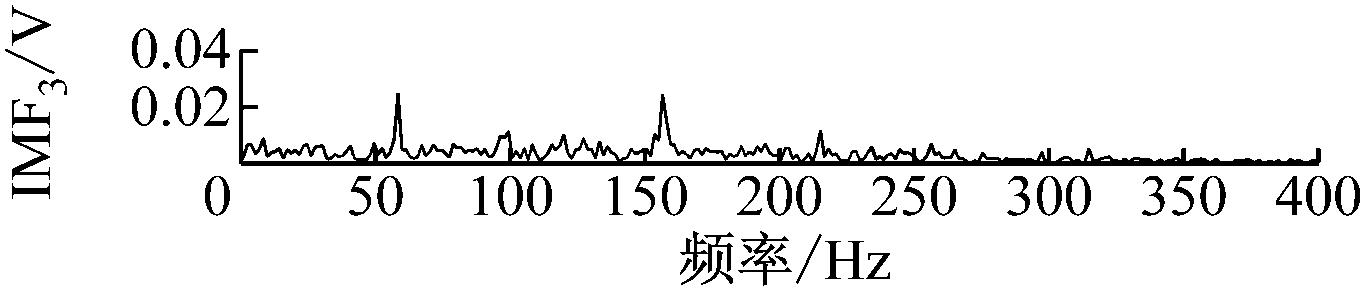





图5 内圈信号EEMD分解后IMF1—IMF8的包络谱
Fig.5 Envelope spectrum of IMF1—IMF8after
inner ring signal is decomposed by EEMD
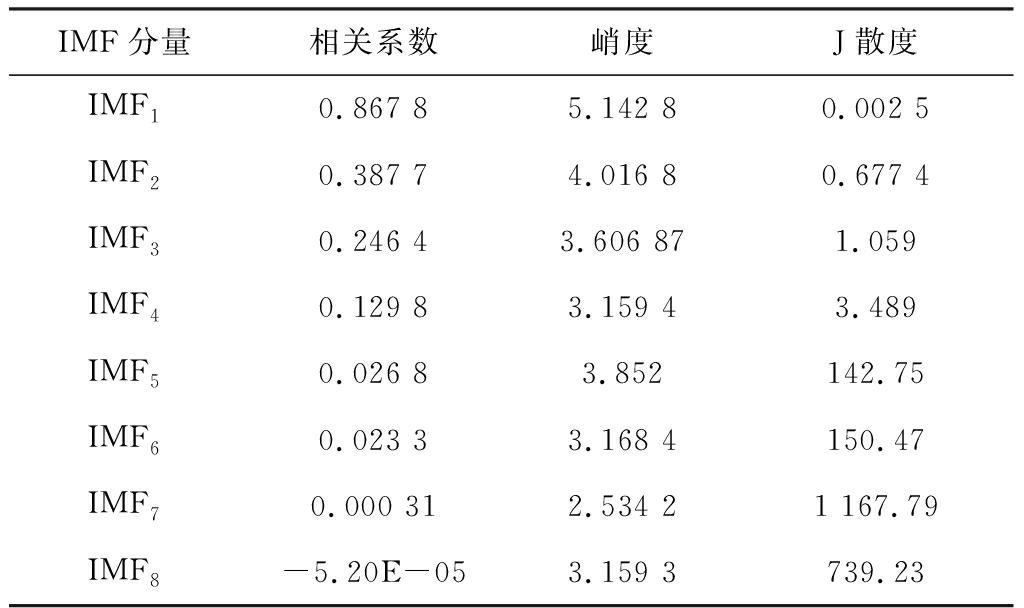
选取转频、二倍转频、内圈故障特征频率与二倍转频的差、内圈故障特征频率处的幅值作为特征向量,计算IMF1—IMF8分量和原始振动信号的相关系数、J散度值、峭度值,并且相关系数按从大到小的顺序排列,结果见表1。
由表1可知,相邻2个相关系数的最大差值在IMF1和IMF2之间,依据相关系数准则,前2阶IMF为有效分量,应予以保留。同时,IMF1和IMF2与原始振动信号的J散度小于设定的剔除域1,依据J散度准则,应予以保留。IMF1、IMF2和IMF3的峭度值均大于3,依据峭度准则,也应予以保留。因此,有效IMF分量为IMF1和IMF2。
表1 IMF分量与内圈原始振动信号的相关系数、
J散度及各IMF分量的峭度
Table 1 Correlation coefficient and J divergence between
each IMF component and original vibration signal of inner
ring, kurtosis value of each IMF component
对IMF1和IMF2分量进行叠加重构,重构后信号峭度值为5.7,比原始信号的峭度值(5.5)有所增加;如对IMF1、IMF2和IMF3分量进行叠加重构,重构后信号峭度值为5.6,可见按文中提出的准则及其阈值选取IMF能够更有效地增强故障冲击信息。
内圈重构信号频谱如图6所示,对比图3所示的原始信号频谱可以看出,重构后信号的低频分量得到削弱,说明所提方法能滤除低频干扰,突出故障分量,提高信噪比。
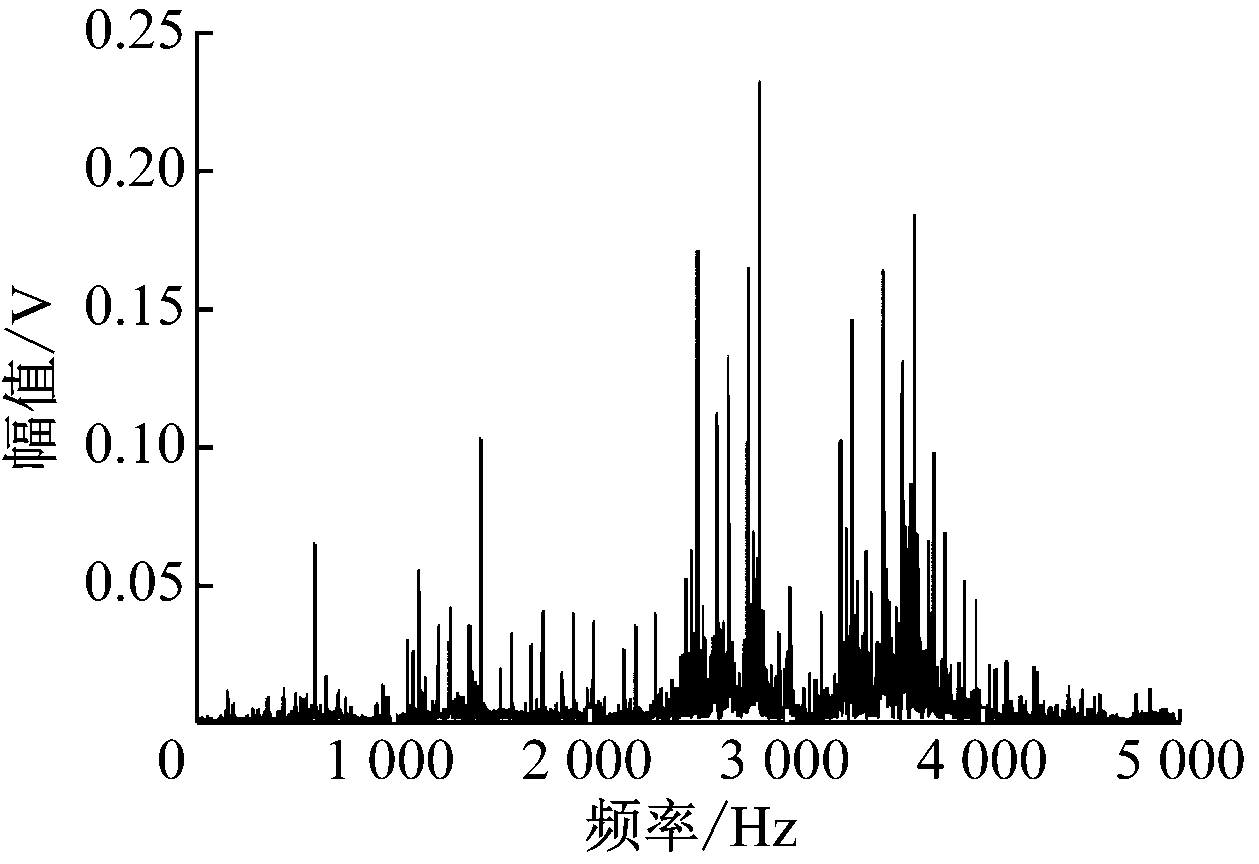
图6 内圈重构信号频谱
Fig.6 Spectrum of inner ring reconstruction signal
对重构后的信号进行Hilbert 和傅里叶变换,得到其包络谱,如图7所示。
从图7可以看出,轴承内圈故障特征频率(156.7 Hz)处幅值为0.27 V,大于原始信号包络谱的故障特征频率幅值0.13 V,而且其余频率峰值也有所减小。
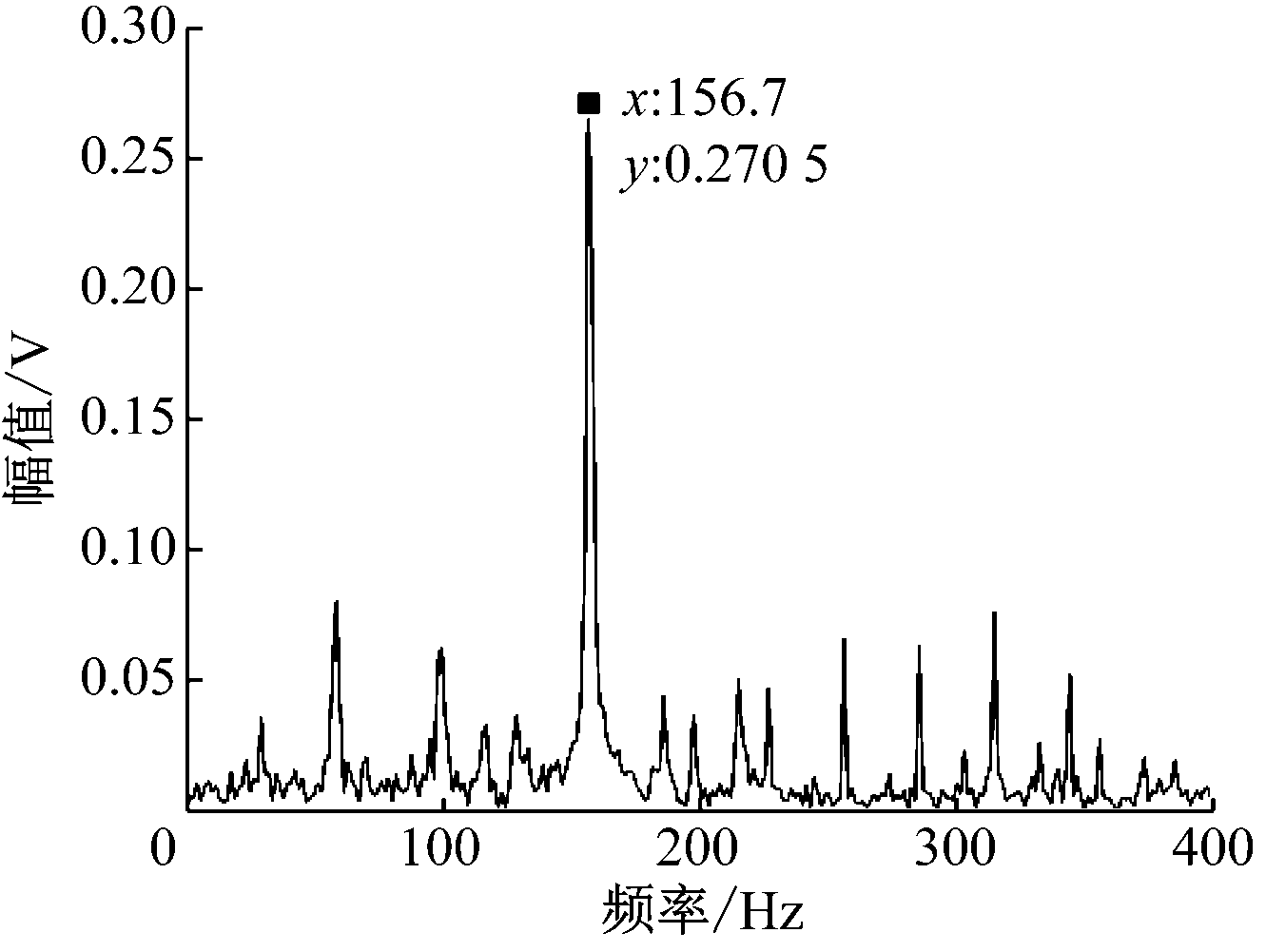
图7 内圈重构信号包络谱
Fig.7 Envelope spectrum of inner ring
reconstruction signal
4 结语
针对滚动轴承早期故障时振动信号的冲击特征微弱、频谱成分复杂、具有非线性非平稳等特点,提出了基于多准则融合的滚动轴承振动信号消噪方法。重点介绍了IMF分量相关系数、J散度及峭度的计算及其相关阈值选取,给出了有效IMF分量的判断依据。将相关系数准则、J散度准则、峭度准则进行融合,选取有效的IMF分量,并进行信号重构。实验结果表明,重构后信号的低频分量得到削弱,说明所提方法能滤除低频干扰,突出故障分量,提高信噪比。
参考文献:
[1] 郭艳平,颜文俊,包哲静,等.基于经验模态分解和散度指标的风力发电机滚动轴承故障诊断方法[J].电力系统保护与控制,2012,40(17):83-87.
GUO Yanping,YAN Wenjun,BAO Zhejing,et al.Fault diagnosis of bearing in wind turbine based on empirical mode decomposition and divergence index[J].Power System Protection and Control,2012,40(17):83-87.
[2] 李辉,郑海起,唐力伟.声测法和经验模态分解在轴承故障诊断中的应用[J].中国电机工程学报,2006,26(15):124-128.
LI Hui,ZHENG Haiqi,TANG Liwei.Application acoustic emission and empirical mode decomposition to faults diagnosis of bearing[J].Proceedings of the CSEE,2006,26(15):124-128.
[3] 程军圣,于德介,杨宇.基于SVM和EMD包络谱的滚动轴承故障诊断方法[J].系统工程理论与实践,2005(9):131-136.
CHENG Junsheng,YU Dejie,YANG Yu.A fault diagnosis approach for roller bearing based on SVM and EMD envelope spectrum[J].Systems Engineering Theory & Practice,2005(9):131-136.
[4] 雷亚国.基于改进Hilbert-Huang变换的机械故障诊断[J].机械工程学报,2011,47(5):71-77.
LEI Yaguo.Machinery fault diagnosis based on improved Hilbert-Huang transform[J].Journal of Mechanical Engineering,2011,47(5):71-77.
[5] 隋文涛,张丹, WANG Wilson.基于EMD和MKD的滚动轴承故障诊断方法[J].振动与冲击,2015,34(9):55-59.
SUI Wentao,ZHANG Dan, WANG Wilson. Fault diagnosis of rolling element bearings based on EMD and MKD[J].Journal of Vibration and Shock,2015,34(9):55-59.
[6] 周智,朱永生,张优云,等.基于EEMD和共振解调的滚动轴承自适应故障诊断[J].振动与冲击,2013,32(2):76-80.
ZHOU Zhi,ZHU Yongsheng,ZHANG Youyun,et al.Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J].Journal of Vibration and Shock,2013,32(2):76-80.
[7] 马宏伟,张大伟,曹现刚,等.基于EMD的振动信号去噪方法研究[J].振动与冲击,2016,35(22):38-40.
MA Hongwei,ZHANG Dawei,CAO Xiangang,et al.Vibration signal de-noising method based on empirical mode decomposition[J].Journal of Vibration and Shock,2016,35(22):38-40.
[8] 丁常富,蔡志成.EMD中有效IMF选取方法的研究[J].热力发电,2014,43(1):36-40.
DING Changfu,CAI Zhicheng. Methods of selecting valid IMF in EMD[J].Thermal Power Generation,2014,43(1):36-40.
[9] 黄中华,谢雅.基于Hilbert变换的滚动轴承内环和外环故障诊断[J].中南大学学报(自然科学版),2011,42(7):1992-1996.
HUANG Zhonghua,XIE Ya.Fault diagnosis of roller bearing with inner and external fault based on Hilbert transformation[J].Journal of Central South University(Science and Technology),2011,42(7):1992-1996.