0 引言
随着电力电子技术的迅速发展, 煤矿电力系统中电网结构、负荷特性有了显著的变化，井下非线性用电设备变得更加复杂，给电网注入大量谐波[1]，使得供配电线路的电压降低，造成电网容量浪费。煤矿电网中公共连接点(Point of Common Coupling，PCC)处的谐波污染是由煤矿电力系统侧和用户侧共同决定的。为了更好地管理谐波，同时满足煤矿供电方和用户的利益需求，就需要估算电力系统的谐波电压、阻抗和用户侧谐波发射水平，对谐波源进行责任划分[2-4]。谐波发射水平数值大的一方承担的谐波责任多。
多元线性回归是最常用的谐波发射水平评估方法。计算谐波电压、阻抗时需要对大量数据进行回归分析处理，数据量的不足和模型中变量的线性相关性都会导致共线性问题[5]，使得估计值受到异常值影响，从而使得求取的回归系数不准确。岭回归法[6-9]是一种专用于共线性数据分析的偏估计回归方法。将岭回归估计应用在估计谐波发射水平上可以有效解决二元线性回归不能处理的共线性问题，减小异常值的影响，使回归系数更精确，使回归模型更稳健[10]。
本文介绍了岭回归估计方法的原理，通过Matlab仿真计算谐波电压、阻抗，并对二元线性回归和岭回归估计方法进行对比，验证将岭回归估计应用在煤矿谐波责任定量划分中的优越性。
1 谐波源责任划分方法原理
1.1 岭回归原理
多元线性回归分析里最常见的问题是多重共线性问题，该问题存在于回归方程的自变量X之间。XTX的特征量中至少有1个很接近于零，使得|XTX|≈0，采用多元线性回归估计时，回归系数β=(β0,β1,…，βp)′(p=0,1,…)的估计量
将产生很大的均方误差，使回归系数不稳定。为了解决该问题，岭回归估计方法在回归系数矩阵中添加了kI矩阵。岭回归表达式为
(1)
式中：k为岭回归估计的岭参数；I为单位矩阵；Y为回归方程的因变量。
k值是变化的，
会随着k的变化而变化，从而形成一个回归系数的估计簇。为了使估计误差最小，需要对岭参数进行合理选择。一般用岭迹法来确定k的值。
1.2 基于岭回归估计的谐波发射水平计算
首先建立系统侧和用户侧等效电路，如图1所示。其中，Vs，Zs为系统侧谐波电压和谐波阻抗；Ic，Zc为用户侧谐波电流和谐波阻抗；Ipcc，Vpcc为PCC处谐波的谐波电流、谐波电压。
图1 系统侧和用户侧等效电路
Fig.1 System side and user side equivalent circuits
根据图1可得
Vs=Vpcc+IpccZs
(2)
将式(2)展开可得回归方程：
Vsx=Vpccx+IpccxZsx-IpccyZsy
(3)
Vsy=Vpccy+IpccyZsx+IpccxZsy
(4)
式(3)、式(4)中的自变量为Ipccx，Ipccy，因变量为Vpccx，Vpccy。根据建立的回归方程，得到回归系数Vsx，Vsy，Zsx，Zsy，再根据岭回归计算结果求出谐波发射水平。具体计算步骤如下：
(1) 将式(3)、式(4)中的自变量和因变量进行中心化和标准化处理，分别用n×p阶矩阵X和n×1阶矩阵Y表示，得
(5)
(6)
式中：xij，yi分别为处理前自变量和因变量矩阵中的元素；Xij，Yi分别为与xij，yi对应的经过中心化和标准化处理后的元素；
为X中j列元素的平均值；
为Y中所有元素的平均值；1≤i≤p；1≤j≤n。
(2) 由式(5)得到矩阵X，计算XTX的特征量，将特征量矩阵与kI相加得到对角矩阵，对其求逆，以提高运算效率。
(3) 通过观察岭迹图的曲线来确定k值。
(4) 确定k值所对应的回归系数，对多组计算结果进行平均，得到谐波阻抗和电压：
(7)
(8)
式中:Zsxi，Zsyi分别为谐波阻抗Zs的实部和虚部;Vsxi，Vsyi分别为谐波电压Vs的实部和虚部。
(5) 在图1中，谐波源及系统侧分别被等效为恒流源、恒压源，谐波源内阻远大于系统内阻，即Zc>>Zs，因此，用户侧谐波发射水平可近似为
(9)
2 仿真分析
煤矿电力系统三次谐波发射水平仿真模型如图2所示。提取模型中PCC的谐波电压和谐波电流，通过二元线性回归法、岭回归法进行对比分析。
仿真参数设置：基波频率为50 Hz，用户侧3次谐波电流源与系统侧3次谐波电压源分别为15∠48° A，50∠53.1° V。系统侧与电源侧采用均匀分布原则，两侧谐波阻抗均匀分布，用户侧3次谐波阻抗为(380+j300)Ω；系统侧3次谐波阻抗为(2+4j)Ω。
图2 谐波发射水平仿真模型
Fig.2 Simulation model of harmonic emission level
对PCC的电压、电流进行采样，如图3所示。
(a) 谐波电流
(b) 谐波电压
图3 PCC的3次谐波电压、电流采样波形
Fig.3 Sampling waveforms of the 3rd harmonic voltage and current of PCC
分别抽取1 440个点，每连续60个点的数据为1组，总共分成24组，然后对各组分别进行二元线性回归和岭回归分析，最后计算出谐波阻抗。
分析仿真数据可知，3次谐波电压平均值为101.23 V；由仿真得到的用户侧谐波发射水平为ΔVc-cont=51.23 V，污染水平ΔVp-level=50.61%。
对PCC的谐波电压、电流波形中的24组数据进行二元线性回归分析，结果如图4所示。
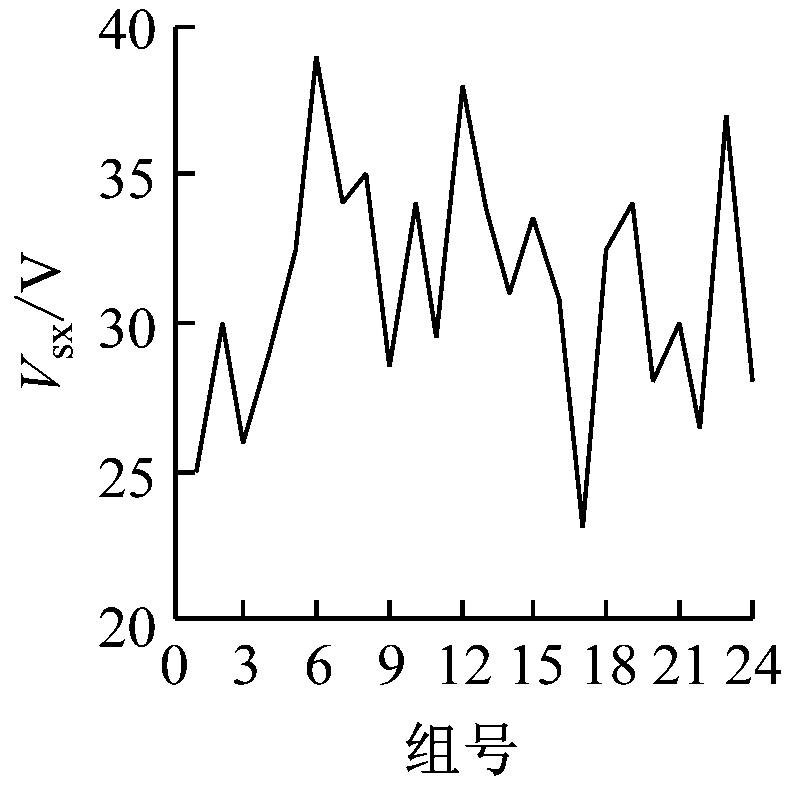
(a) 系统侧3次谐波电压
(b) 系统侧谐波阻抗
图4 二元线性回归法分析结果
Fig.4 Analysis results of binary linear regression method
利用图4的数据可以求得系统侧谐波电压为
(10)
系统侧谐波阻抗为
(11)
估计值与理想值的误差为
(12)
根据式(9)可得用户侧3次谐波发射水平为
(13)
污染水平ΔVp-level为
(14)
对24组数据进行岭回归估计，得到系统侧3次谐波电压和阻抗，如图5所示。
(a) 系统侧3次谐波电压
(b) 系统侧谐波阻抗
图5 岭回归估计法分析结果
Fig.5 Analysis results of ridge regression estimation method
利用图5的数据可以求得系统侧谐波电压为
(15)
系统侧谐波阻抗、估计值与理想值的误差分别为
(16)
(17)
同理可得用户侧3次谐波发射水平ΔVc-cont=48.528 V，污染水平ΔVp-level=47.939%。
利用二元线性与岭回归估计方法求解的用户谐波污染水平及估计值与理想值的误差数据对比见表1。
表1 二元线性回归与岭回归估计方法分析结果对比
Table 1 Comparison of analysis results between binary linear regression and ridge regression estimation method %
由表1可知，2种方法得到的结果和理想值都比较接近，而岭回归估计方法的结果优于二元线性回归方法，因为岭回归相比二元回归更易于解决共线性问题。用岭回归估计方法分析得到的用户侧谐波污染水平为47.939%，占比接近50%，说明系统侧和用户侧应承担的谐波责任接近。
3 结语
通过岭回归估计方法计算谐波电压、阻抗来估计谐波发射水平，实现了煤矿电力系统谐波源责任划分。仿真结果表明，与二元线性回归方法相比，岭回归估计方法可以更有效地解决共线性问题，使回归系数的精度更加准确，从而得到更准确的谐波发射水平。通过定量划分谐波责任，可以同时满足煤矿供电方和用户之间的利益，避免电能质量纠纷。
参考文献(References)：
[1] 刘秀兰,栾逢时.电力谐波对电力系统的影响及治理方法[J].电气应用,2015,34(增刊1):125-128.
[2] 华回春,贾秀芳,曹东升,等.电能质量数据交换格式下的谐波责任估计[J].电网技术,2013,37(11):3110-3117.
HUA Huichun,JIA Xiufang,CAO Dongsheng,et al.Harmonic contribution estimation under power quality data interchange format[J].Power System Technology,2013,37(11):3110-3117.
[3] 许加柱,庞丽忠,张志文,等.多谐波源用户的谐波责任分摊的定量分析[J].电力自动化设备,2012,32(12):38-42.
XU Jiazhu,PANG Lizhong,ZHANG Zhiwen,et al.Quantitative analysis for harmonic responsibility proration among multiple harmonic sources[J].Electric Power Automation Equipment,2012,32(12):38-42.
[4] 刘晓璇.多谐波源责任分摊方法的研究[D].保定:华北电力大学,2016.
[5] 杨梅,肖静,蔡辉.多元分析中的多重共线性及其处理方法[J].中国卫生统计,2012,29(4):620-624.
[6] 朱尚伟,李景华.岭回归参数的两个预期约束[J].统计与决策,2015(22):71-74.
[7] 杨景,阳一雄,许欢欢,等.基于广义岭回归的谐波阻抗分析与谐波评估法[J].电力学报,2012,27(2):99-102.
YANG Jing,YANG Yixiong,XU Huanhuan,et al.The harmonic impedance analysis and assessment method based on the generalized ridge regression[J].Journal of Electric Power,2012,27(2):99-102.
[8] 周晓宇,颜学峰,钱锋.基于径向基函数的非线性岭回归方法及仿真研究[J].系统仿真学报,2006,18(10):2738-2741.
ZHOU Xiaoyu,YAN Xuefeng,QIAN Feng.Nonlinear ridge regression modeling method based on radial basis function and its simulation research[J].Journal of System Simulation,2006,18(10):2738-2741.
[9] 曾繁会,吕渭济.基于MATLAB的岭回归分析程序设计及其应用[J].辽宁工程技术大学学报(自然科学版),2001,20(6):838-839.
ZENG Fanhui,LYU Weiji.Program design and the use of ridge regression based on MATLAB[J].Journal of Liaoning Technical University (Natural Science Edition),2001,20(6):838-839.
[10] 杨楠.岭回归分析在解决多重共线性问题中的独特作用[J].统计与决策,2004(3):14-15.