图1 DHNN结构
Fig.1 DHNN structure
徐佳, 陈俊智, 刘晨毓, 王佳信, 龙刚, 李春义
(昆明理工大学 国土资源工程学院, 云南 昆明 650093)
摘要:针对现有岩爆预测方法权重的确定带有随意性和主观性问题,提出了一种岩爆烈度分级预测的离散Hopfield神经网络(DHNN)模型。该模型选取应力系数、岩石脆性系数及弹性能量指数作为评价指标,将岩爆等级分为强岩爆、中等岩爆、弱岩爆及无岩爆4级,然后进行编码,不需要对样本数据进行归一化处理,只需转换成“1”和“-1”的二值型模式,编码简单,网络迭代次数少,具有很好的联想记忆功能,使岩爆烈度分级预测更加科学合理,可为深部地下工程岩爆烈度分级预测提供一种新途径。典型岩爆工程实例预测结果证明了该模型的正确性。
关键词:煤炭开采; 深部地下工程; 岩爆烈度; 分级预测; 弹性能量; 岩石脆性系数; 离散Hopfield神经网络
岩爆是高地应力条件下,岩体中聚积的弹性应变能因洞室开挖而释放,导致岩体产生迸裂、弹射等脆性破坏现象[1]。随着开采深度的增加,深部开采与浅部开采所处的环境明显不同,深部开采所处的环境为高地应力、高地温、高岩溶水压和强烈的开采扰动,而浅部则表现为脆性岩体在深部高应力条件下转变为延性,在开采卸载条件下又由延性向脆性转化,易于产生岩爆。随着地下工程向深部发展,岩爆发生越来越频繁,已成为目前深部岩体工程中迫切需要解决的难题。因此,对岩爆进行预测具有重要的现实意义。
近年来,随着模糊概率[2]、人工神经网络[3]、蚁群聚类[4]、组合赋权[5]、正态云[6]及加权距离判别[7]等模型在工程中的应用,使得岩爆烈度分级较为科学合理。以上模型在工程中都获得了一些成果,但仍存在一定的局限性。例如,文献[2]中模糊概率模型存在隶属度、权重选取具有随意性和主观性的缺陷;文献[3]中所采用的人工神经网络模型其隐含层没有确定性法则,需要根据经验反复试算才能获得预测结果,学习收敛速度慢,而且易陷入局部最优值[8];文献[7]从主成分方向角度考虑各因素权重,其权重的考虑具有主观性,也没有考虑到各因素是否适用于主成分分析。岩爆与岩石最大切应力σθ、单轴抗压强度σc、单轴抗拉强度σt及岩石的弹性能量指数Wet之间存在着复杂的不确定性关系,正因如此,建立有效的岩爆预测模型显得十分必要。
智能岩石力学理论将人工智能与岩石力学交叉、融合,使得岩石力学问题的研究更全面、更系统[9]。基于该思想,本文引入一种离散Hopfield神经网络(Discrete Hopfield Neural Network,DHNN)模型,它是一种单层反馈非线性网络,每一个节点的输出均反馈到其他节点的输入,整个网络都不存在自反馈。DHNN主要用于联想记忆,即DHNN是利用连接权值存储标准分类样本,实现测试样本分类联想记忆功能;当导入一组初始值时,DHNN可在能量函数单调递减的条件下到达稳定点。DHNN模型模拟的是人类智慧之一:人类所谓的“触景生情”,就是看见一些类似同过去接触的景象,容易产生对过去景象的回味和思忆[10]。鉴于此,本文提出了岩爆烈度分级预测的DHNN模型,并以国内外典型岩爆工程实例验证模型的可靠性和有效性,为小样本、部分数据缺失和多指标的岩爆烈度分级预测提供一种新途径。
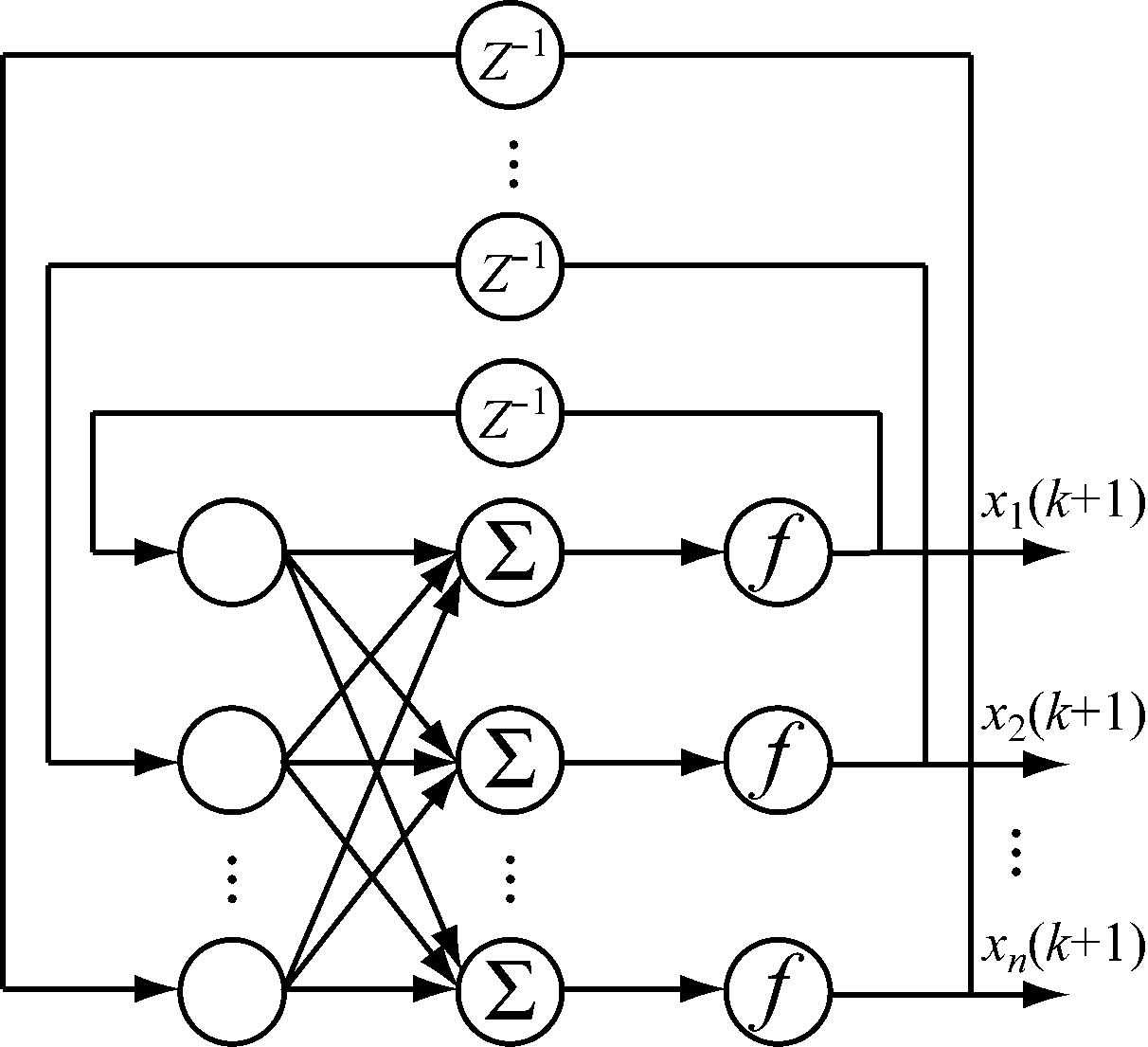
DHNN是一种单层的全反馈网络,其网络结构如图1所示。

图1 DHNN结构
Fig.1 DHNN structure
DHNN的联想记忆可分为2个阶段[11-12]:一是记忆阶段,也称为存储阶段或学习阶段;二是联想阶段,也称为恢复阶段或回忆阶段。
设DHNN的节点个数为n,每个节点的状态为1和-1,第i个节点在k时刻的状态为xi(k) ∈{1,-1},其中i=1,2,…,n。设整个DHNN在k时刻的状态为X(k),则X(k)可以表示为
X(k)=[x1(k),x2(k),…,xn(k)]
(1)
针对DHNN的反馈连接,DHNN通过单位延迟Z-1可得第i个节点在k+1时刻的状态为
(2)
式中:wij为第i个与第j个节点间的权值矩阵;f(a)为符号函数,f(a)![]()
DHNN模型在k+1时刻的输出为X(k+1),可表示为
X(k+1)=[x1(k+1),x2(k+1),…,xn(k+1)]
(3)
X(k+1)的矩阵形式为
X(k+1)=f(WX(k))
(4)
式中W为DHNN的权值矩阵。
根据文献[5]对岩爆烈度评价指标体系的选取,选取的岩爆烈度分级的影响因素如下:最大切应力σθ、单轴抗压强度σc、单轴抗拉强度σt及岩石的弹性
能量指数Wet,并以应力系数σθ/σc、岩石脆性系数σc/σt及弹性能量指数Wet作为评价指标评判岩爆的烈度分级。将岩爆等级分为强岩爆、中等岩爆、弱岩爆及无岩爆4级,分别以Ⅰ、Ⅱ、Ⅲ和Ⅳ表示,岩爆烈度分级标准[6]见表1。采用16个国内外典型岩爆工程实例作为学习样本 (表2)。
表1 岩爆烈度分级标准
Table 1 The classification standard of rockburst intensity
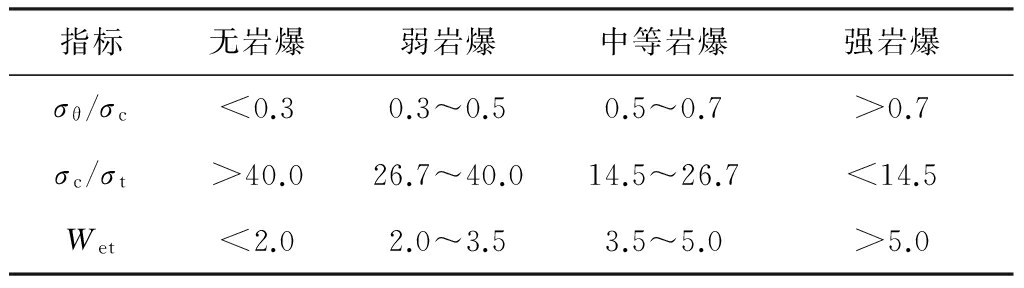
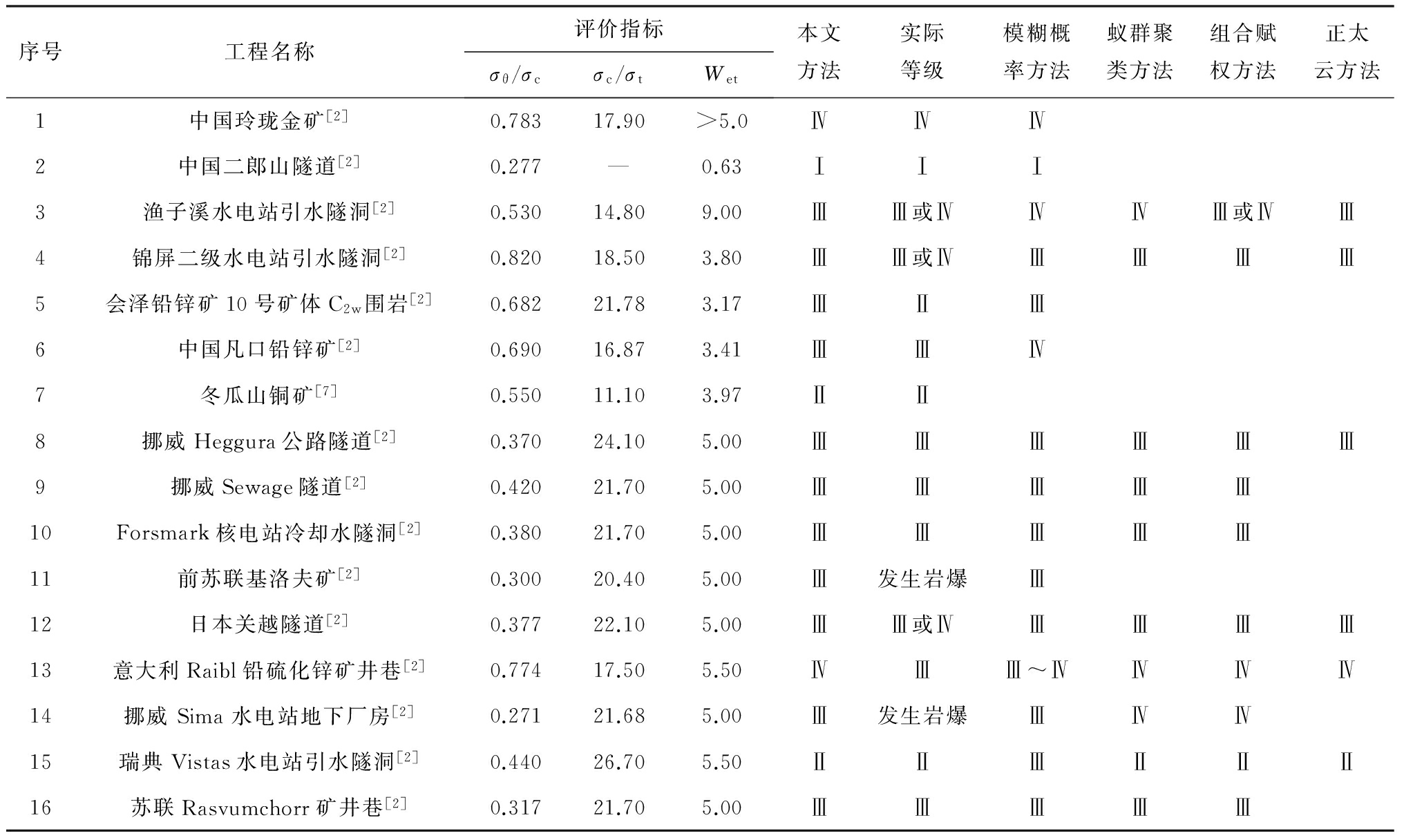
表2 典型工程岩爆实例预测结果
Table 2 The prediction results of rockburst of typical engineering examples
DHNN利用连接权值将表1中4种岩爆分级标准储存起来,然后进行编码,编码原则:满足某个分级标准的范围时,用“1”表示,反之用“-1”表示。4种岩爆烈度分级指标编码如图2所示,分别用“●”(表示“1”)和“○”(表示“-1”)表示。根据表1的岩爆分级标准将表2中的样本进行编码。以1—4号样本为例进行编码(图3)。其他样本编码同理。
16个样本的DHNN模型仿真结果如图4—图7及表2所示。图中,Class1—Class4为岩爆烈度等级Ⅰ,Ⅱ,Ⅲ,Ⅳ;Pre-sim1—Pre-sim16为评价指标的编码;Sim1—Sim16为评价结果。限于篇幅,仅以图4为例进行具体分析。由图4可以看出,第1行与图2对应,表示4个标准的岩爆烈度分级指标编码;第2行与图3对应,第3行表示1—4号样本的预测结果。结合表2可以看出,1—4号样本的判别结果与实际结果基本一致。
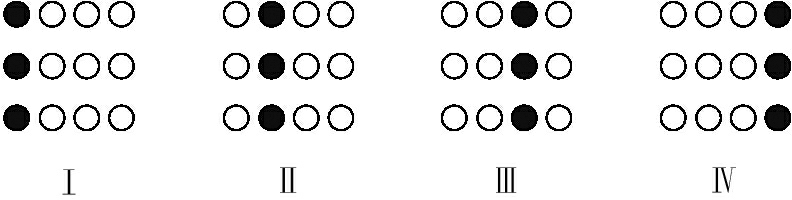
图2 岩爆烈度分级指标编码
Fig.2 The code of classification index of rockburst intensity

图3 1—4号岩爆样本的编码
Fig.3 Coding of rockburst samples No.1 to No.4

图4 1—4号样本岩爆烈度分级评价结果
Fig.4 Classification evaluation results of rockburst intensity of samples No.1 to No.4

图5 5—8号样本岩爆烈度分级评价结果
Fig.5 Classification evaluation results of rockburst intensity of samples No.5 to No.8
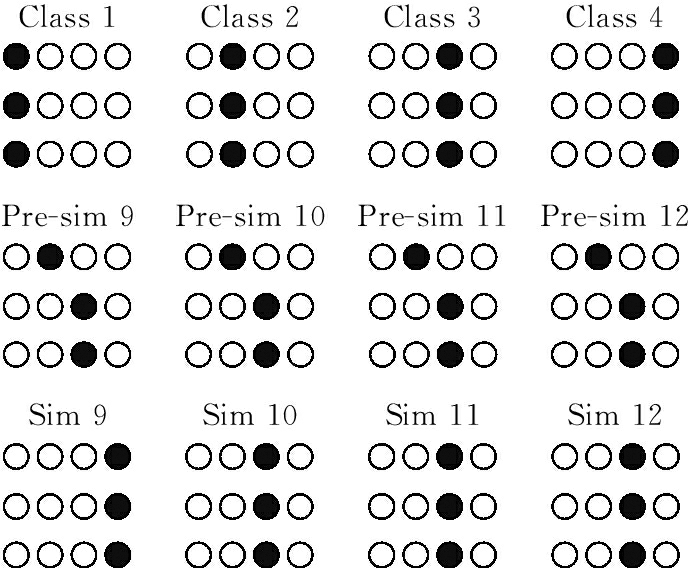
图6 9—12号样本岩爆烈度分级评价结果
Fig.6 Classification evaluation results of rockburst intensity of samples No.9 to No.12
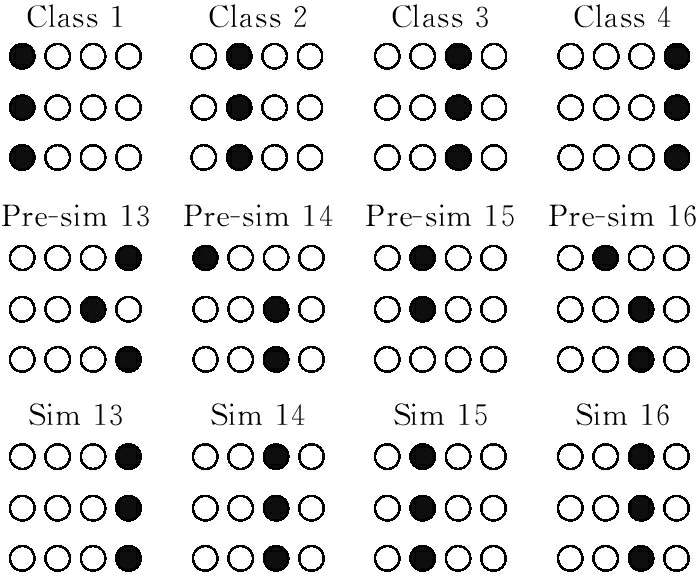
图7 13—16号样本岩爆烈度分级评价结果
Fig.7 Classification evaluation results of rockburst intensity of samples No.13 to No.16
其中,会泽铅锌矿10号矿体C2w围岩和意大利Raibl铅硫化锌矿井巷分别误判为Ⅲ级(实际为Ⅱ级)和Ⅳ级(实际为Ⅲ级)。由表2可以看出,DHNN模型评价结果偏高,但从工程安全的角度考虑是可行的。2号样本在缺损σc/σt指标的情况下,仍可以科学、快速地判断岩爆等级为Ⅰ,且与实际结果一致。
DHNN模型对16个岩爆样本进行判别,其中2号和13号样本判别存在一定的偏差,其余样本判别均与实际相符,模型的正判率为87.5%,说明将DHNN模型应用于岩爆预测是可行的。
(1) 提出了一种岩爆烈度分级评价模型——DHNN模型,该模型具有有联想记忆功能,可对岩爆等级进行编码,不需要对样本数据进行归一化处理,只需将其转换成“1”和“-1”的二值型模式,编码简单,网络迭代次数少,使岩爆烈度分级预测更为科学合理,为地下工程岩爆烈度分级判别提供了一种新的思路。
(2) 典型岩爆工程实例预测结果表明,DHNN模型具有较好的评价效果,其正判率为87.5%,可为小样本、部分数据缺损和多指标的岩爆烈度分级预测提供一种很好的思路。
(3) 但DHNN模型可能存在很多伪稳定点,当一些实测指标值较高而一些实测指标值较低时,DHNN模型得不到确切的分类。利用智能优化算法全局搜索能力对DHNN模型的联想记忆稳态进行优化,有待于深入研究。
参考文献(References):
[1] 陈鹏宇,余宏明,师华鹏. 基于权重反分析和标准化模糊综合评价的岩爆预测模型[J]. 岩石力学与工程学报,2014,33(10):2154-2160.
CHENG Pengyu,YU Hongming,SHI Huapeng.Prediction model for rockburst based on weighted back analysis and standardized fuzzy comprehensive evaluation[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(10):2154-2160.
[2] 刘章军,袁秋平,李建林. 模糊概率模型在岩爆烈度分级预测中的应用[J]. 岩石力学与工程学报,2008,27(增刊1):3095-3103.
LIU Zhangjun,YUAN Qiuping,LI Jianlin.Application of fuzzy probability model to prediction of classification of rockburst intensity[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(S1):3095-3103.
[3] 张光存,高谦,杜聚强,等. 基于人工神经网络及非线性回归的岩爆判据[J]. 中南大学学报(自然科学版),2013,44(7):2977-2981.
ZHANG Guangcun,GAO Qian,DU Juqiang,et al.Rockburst criterion based on artificial neural networks and nonlinear regression[J].Journal of Central South University (Science and Technology),2013,44(7):2977-2981.
[4] 高玮. 基于蚁群聚类算法的岩爆预测研究[J]. 岩土工程学报,2010,32(6):874-880.
GAO Wei.Prediction of rockburst based on ant colony clustering algorithm[J].Chinese Journal of Geotechnical Engineering,2010,32(6):874-880.
[5] 裴启涛,李海波,刘亚群,等.基于组合赋权的岩爆倾向性预测灰评估模型及应用[J].岩土力学,2014,35(增刊1):49-56.
PEI Qitao,LI Haibo,LIU Yaqun,et al.A grey evaluation model for predicting rockburst proneness based on combination weight and its application[J]. Rock and Soil Mechanics,2014,35(S1):49-56.
[6] 王迎超,靖洪文,张强,等. 基于正态云模型的深埋地下工程岩爆烈度分级预测研究[J]. 岩土力学,2015,36(4):1189-1194.
WANG Yingchao,JING Hongwen,ZHANG Qiang,et al.A normal cloud model-based study of grading prediction of rockburst intensity in deep underground engineering[J]. Rock and Soil Mechanics,2015,36(4):1189-1194.
[7] 罗磊,曹平. 深部巷道岩爆加权距离判别法模型的分析和应用[J]. 中南大学学报(自然科学版),2012,43(10):222-226.
LUO Lei,CAO Ping.Model of weighted distance discriminant analysis and application for deep roadway[J]. Journal of Central South University (Science and Technology),2012,43(10):222-226.
[8] 王佳信,周宗红,赵婷,等. 基于Alpha稳定分布概率神经网络的围岩稳定性分类研究[J]. 岩土力学,2016,37(增刊2):649-657.
WANG Jiaxin,ZHOU Zonghong,ZHAO Ting,et al. Application of Alpha stable distribution probabilistic neural network to classification of surrounding rock stability assessment[J]. Rock and Soil Mechanics,2016,37(S2):649-657.
[9] 王佳信,周宗红,张继华,等. 煤与瓦斯突出危险性预测的SaS-PNN模型及应用[J]. 传感技术学报,2017,30(7):1112-1118.
WANG Jiaxin,ZHOU Zonghong,ZHANG Jihua,et al.SaS-PNN model for forecast of coal and gas outburst risk and its application[J].Chinese Journal of Sensors and Actuators,2017,30(7):1112-1118.
[10] 刘胜,刘娜,杨育,等.危险源安全评价的离散Hopfield神经网络[J].重庆大学学报(自然科学版),2013,36(4):26-32.
LIU Sheng,LIU Na,YANG Yu,et al.Safety evaluation of hazards based on discrete Hopfield neural network[J].Journal of Chongqing University(Natural Science Edition),2013,36(4):26-32.
[11] 常利营,卢建移,段波,等. 基于Hopfield网络的地下工程围岩稳定性分类[J]. 岩土工程学报,2011,33(增刊1):194-197.
CHANG Liying,LU Jianyi,DUAN Bo,et al.Stability classification of adjoining rock of underground engineering based on Hopfield network[J]. Chinese Journal of Geotechnical Engineering,2011,33(S1):194-197.
[12] 李荣,乔俊飞,韩红桂.一种改进型离散Hopfield学习算法[J]. 控制与决策,2014,29(2):241-245.
LI Rong,QIAO Junfei,HAN Honggui.An improved learning algorithm for discrete Hopfield[J].Control and Decision,2014,29(2):241-245.
XU Jia, CHEN Junzhi, LIU Chenyu, WANG Jiaxin, LONG Gang, LI Chunyi
(Faculty of Land Resource Engineering,Kunming University of Science and Technology, Kunming 650093,China)
Abstract:In view of problems of randomness and subjectivity in determining weight of existing rockburst prediction methods,a discrete Hopfield neural network (DHNN) model for prediction of classification of rockburst intensity was proposed。The model selects stress coefficient, rockbrittleness coefficient and elastic energy index as evaluation index, divides rockburst grade into 4 stages, such as strong rockburst, medium rockburst, weak rockburst and no rockburst, then encodes them. The model needn't normalize sample data with simpler encoding ,lesser iterations of network and better associative memory ability, only be converted to "1" and "-1" of the two value model, therefore, the classification prediction of rockburst intensity is more scientific and reasonable. The model can provide a new way for classification prediction of rockburst intensity in deep underground engineering. The prediction results of typical rockburst engineering examples prove the correctness of the model.
Key words:coal mining; deep underground engineering; rockburst intensity; classification prediction; elastic energy; rock brittleness coefficient; discrete Hopfield neural network
收稿日期:2017-06-22;
修回日期:2017-10-27;
责任编辑:张强。
基金项目:国家自然科学基金资助项目(U1602232)。
作者简介:徐佳(1992-),男,浙江嘉兴人,硕士研究生,主要研究方向为岩石力学,E-mail:522810951@qq.com。通信作者:陈俊智(1974-),男,陕西定边人,副教授,博士,主要研究方向为岩石力学,E-mail:chenjunzhi130@yahoo.com.cn。
引用格式:徐佳,陈俊智,刘晨毓,等.DHNN模型在岩爆烈度分级预测中的应用研究[J].工矿自动化,2018,44(1):84-88.
XU Jia,CHEN Junzhi,LIU Chenyu,et al.Application research of DHNN model in prediction research of classification of rockburst intensity[J].Industry and Mine Automation,2018,44(1):84-88.
文章编号:1671-251X(2018)01-0084-05
DOI:10.13272/j.issn.1671-251x.2017050027
中图分类号:TD31
文献标志码:A 网络出版时间:2017-12-07 17:27
网络出版地址:http://kns.cnki.net/kcms/detail/32.1627.TP.20171206.1510.004.html