
图1 MRR摆臂驱动系统模型
Fig.1 Model of MRR swing arm driving system
刘嘉, 胡晋智
(太原工业学院 机械工程系, 山西 太原 030008)
摘要:针对矿井救灾机器人最大允许体积及质量受限问题,采用单逆变器驱动双电动机形式设计了一种矿井救灾机器人摆臂驱动系统,采取加权求和方法构建了该系统模型,并对该模型双电动机电流关系进行了推导分析。针对煤矿井下复杂工况造成的矿井救灾机器人摆臂负载不一致问题,提出了一种基于有源阻尼机制的矿井救灾机器人摆臂驱动系统平衡控制方法。基于15 kW矿井救灾机器人样机对该方法进行了测试,结果表明该方法可在矿井救灾机器人摆臂负载不一致的情况下实现转矩动态匹配。
关键词:煤矿事故; 救灾机器人; 摆臂驱动; 双机驱动; 平衡控制; 动态转矩平衡; 有源阻尼
为了增强矿山企业发生安全事故时的环境勘测及人员搜救能力,避免事故发生后人员操作引起的二次事故问题,矿井救灾机器人(Mine Rescue Robot,MRR)逐步成为国内外矿山企业、高校的研究热点[1-3]。美国Remotec公司研制的V2型MRR可在1 500 m外进行远程遥控,通过光纤传输矿井环境信息,操纵者能够获得实时视频和易燃、有毒气体浓度信息[4]。卡内基梅隆大学机器人研究中心开发的Groundhog探测机器人可实现井下环境探测、井下立体地图绘制等功能,且机械结构采用四轮导向、液压驱动,可实现原地零半径转弯[5]。中国矿业大学救援技术与装备研究所分别于 2006年、2011年成功研制了CUMT-I型[6-7]、CUMT-II型MRR样机[8-9],均采取主动摆臂形式。由于运行环境恶劣、工况复杂,MRR各摆臂动态负载不匹配现象严重[10-12],且受最大允许体积及质量的限制,MRR无法装备多套驱动装置来完成各摆臂独立控制[13-15]。
针对上述问题,本文采取加权求和方法完成了一种基于单逆变器双电动机的MRR摆臂驱动系统建模,并分析了该模型的稳定性。考虑到复杂工况造成的MRR摆臂负载不一致问题,提出一种基于有源阻尼机制的MRR摆臂驱动系统多机平衡控制方法。基于研制的15 kW MRR实验样机对该方法进行测试,结果表明该方法可在MRR摆臂负载不一致的情况下实现转矩动态匹配,且有源阻尼机制对于转矩动态匹配具有积极意义。
单逆变器双电动机MRR摆臂驱动系统模型如图1所示。逆变器主电路拓扑采取三相电压源逆变器结构,直流母线电压为Udc。S1—S6为开关器件。MRR的2个摆臂均由永磁同步电动机驱动,其三相电流分别为ik1,ik2(k=a,b,c),转子位置角度分别为θr1,θr2,转子角速度分别为ωr1,ωr2。
考虑到运行过程中各摆臂运行状态具有差异性,摆臂驱动系统的电压、电流、磁链等均存在一定误差,如图2所示。Ψr1,Ψr2分别为MRR摆臂驱动系统1号、2号电动机磁链,ΔΨr为双电动机磁链误差,ΔΨdr,ΔΨqr分别为双电动机磁链误差d轴、q轴分量,is1,is2分别为1号、2号电动机电流,Δis为双电动机电流误差, Δids,Δiqs分别为双电动机电流误差d轴、q轴分量。

图1 MRR摆臂驱动系统模型
Fig.1 Model of MRR swing arm driving system
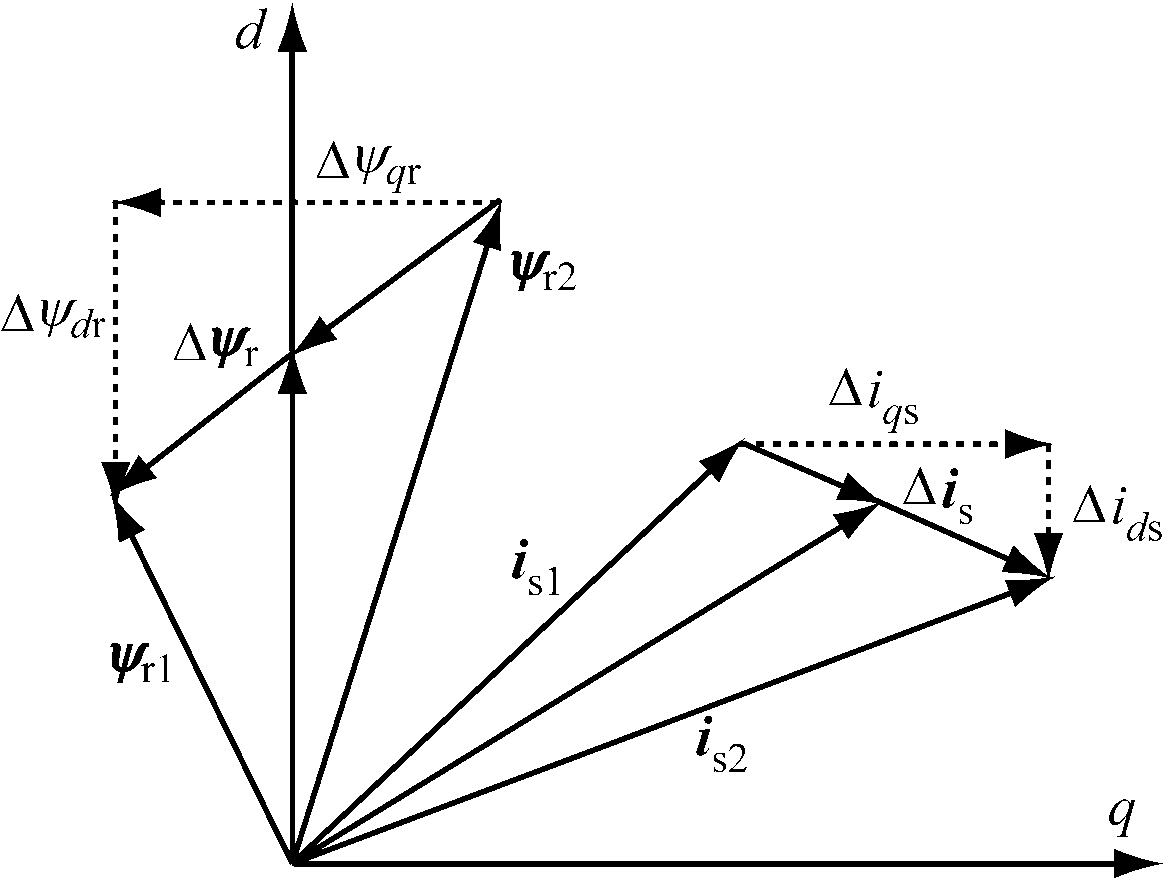
图2 MRR摆臂驱动系统电流、磁链矢量关系
Fig.2 Current and magnetic vector relations of MRR swing arm driving system
引入加权系数km构建MRR摆臂驱动系统加权模型,即
Ψr=kmΨr1+(1-km)Ψr2
ΔΨr=Ψr2-Ψr2
(1)
is=kmis1+(1-km)is2
Δis=is2-is1
(2)
ωr=kmωr1+(1-km)ωr2
Δωr=ωr2-ωr1
(3)
式中:Ψr为MRR摆臂驱动系统加权磁链;is为MRR摆臂驱动系统加权电流;ωr为MRR摆臂驱动系统加权角速度;Δωr为双电动机角速度误差。
令MRR摆臂驱动系统加权磁链Ψr为主定向矢量,建立以Ψr方向为d轴的系统等效模型:
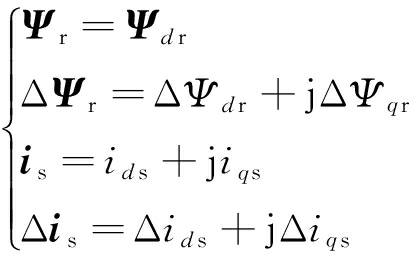
(4)
进一步建立双电动机转矩方程:
Tsum=Te1+Te2=![]() p(Ψr1is1+Ψr2is2)
p(Ψr1is1+Ψr2is2)
(5)
式中:Tsum为系统等效转矩;Te1,Te2分别为1号、2号电动机输出转矩;p为电动机极对数。
将式(1)、式(2)代入式(5),得
Tsum=Te1+Te2= ![]() p[Ψr1-(1-kmΔΨr)][is-(1-kmΔis)]+
p[Ψr1-(1-kmΔΨr)][is-(1-kmΔis)]+ ![]() p(Ψr1+kmΔΨr)(is+kmΔis)
p(Ψr1+kmΔΨr)(is+kmΔis)
(6)
式(6)中加权系数km将决定MRR摆臂驱动系统在负载不平衡情况下的动态响应特性,即
km=![]()
(7)
假设MRR摆臂驱动系统出现负载不平衡现象,1号电动机负载突增,对应加权系数km增大,此时系统以1号电动机为主电动机,保证1号电动机转速快速恢复至期望值。
对于单逆变器双电动机MRR摆臂驱动系统,双电动机采用并联方式连接同一逆变器,任意时刻双电动机端口电压矢量保持一致。考虑到双电动机运行过程中磁链位置的差异性,摆臂驱动系统双电动机电压满足关系:
(8)
式中:vd1,vq1分别为1号电动机电压d轴、q轴分量;vd2,vq2分别为2号电动机电压d轴、q轴分量;θd为1号、2号电动机转子位置角度差,θd=θr1-θr2。
由式(8)可得MRR摆臂驱动系统双电动机电流:
![]()
![]()
![]()
(9)
式中:id1,iq1分别为1号电动机电流d轴、q轴分量;id2,iq2分别为2号电动机电流d轴、q轴分量; Rs为电动机定子电阻;Ls为电动机定子电感。
分析式(9)可知,2号从电动机电流包括2个部分:一部分由1号主电动机电流经坐标变换得到,另一部分由反电动势经电动机阻抗折算得到。可看出电动机定子电阻Rs的占比随加权角速度ωr的增大而减小;无功阻抗分量ωrLs在式(9)中以反对角矩阵形式存在,其收敛时间随加权角速度ωr的增大同步增大,即MRR摆臂驱动系统的稳定性降低。忽略电动机定子电阻Rs,且令电动机加权角速度ωr较大,式(9)可转换为
![]()
![]()
![]()
(10)
从式(10)可看出,2号从电动机电流d轴、q轴分量独立于电动机加权角速度ωr,且仅与1号、2号电动机转子位置角度差θd有关。设1号、2号电动机均为15 kW永磁同步电动机,其设计参数一致:额定转速为750 r/min,极对数为4,永磁体磁链为1 Wb,定子电感d轴、q轴分量分别为0.6,1.2 mH。1号主电动机输出转矩分别为0,12,24 N·m,2号从电动机空载时,2号从电动机电流如图3所示。可看出1号主电动机负载不同时,2号从电动机电流d轴分量id2随θd增大呈先增大后减小趋势,q轴分量iq2随θd呈逐渐减小趋势。可见,1号主电动机负载不同,使得2号从电动机耦合出不同的d轴、q轴电流分量。在双电动机转子位置角度差θd一定时,通过调节1号主电动机电流d轴、q轴分量,可实现对2号从电动机电流d轴、q轴分量的控制,从而调节2号从电动机输出转矩。
MRR摆臂驱动系统动力学方程为
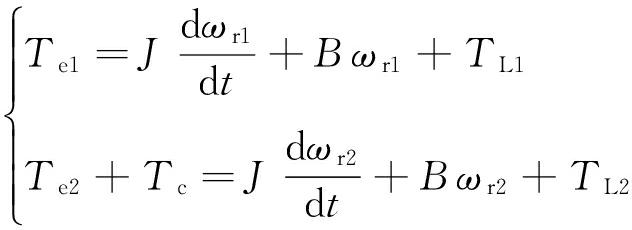
(11)
式中:J为电动机转动惯量;B为摩擦因数;TL1,TL2分别为1号、2号电动机负载转矩;Tc为由双电动机磁链角度误差产生的耦合转矩。
以MRR摆臂驱动系统加权磁链为矢量控制定向磁链,1号主电动机电流q轴分量iq1可精确控制1号电动机输出转矩Te1,耦合转矩Tc可定义为2号从电动机的附加转矩。由式(11)得
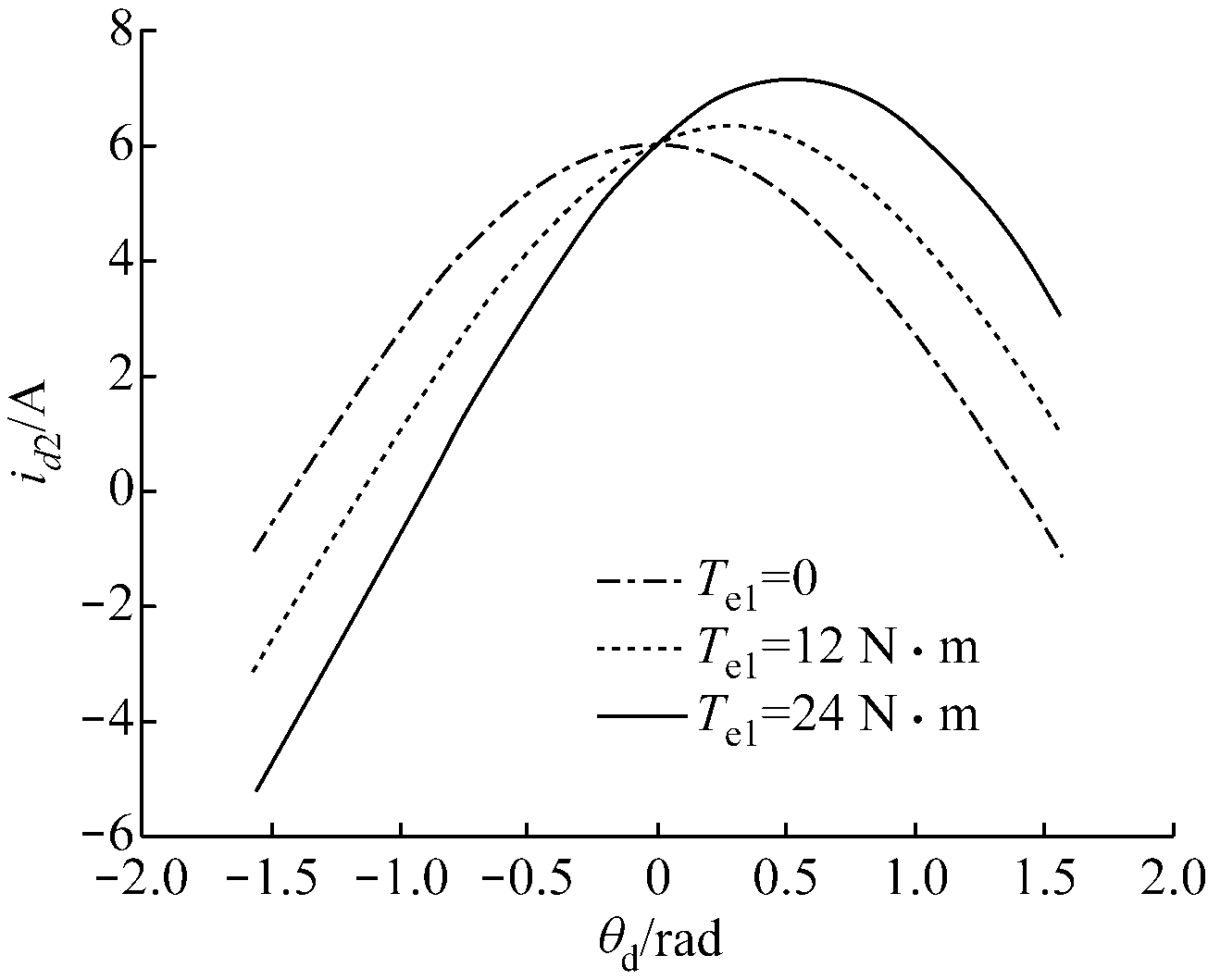
(a) d轴分量

(b) q轴分量
图3 2号从电动机电流
Fig.3 Current of No.2 motor
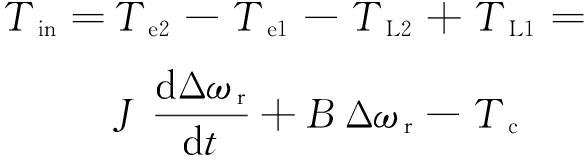
(12)
式中Tin为MRR摆臂驱动系统等效输入转矩。
采用分段线性法令双电动机转子位置角度差θd与耦合转矩Tc呈线性关系,即
Tc=Kθθd
(13)
式中Kθ为分段线性参数。
(14)
式中θ0为MRR摆臂驱动系统双电动机初始磁链误差角。
由此可得Tin与ωr之间的传递函数:
=![]()
(15)
为了保证MRR摆臂驱动系统的稳定性,对式(15)的极点进行分析,其取值为
s1,2=![]() <0
<0
(16)
化简式(16)可得,分段线性参数Kθ需满足Kθ<0,即可保证MRR摆臂驱动系统趋于稳定。由式(14)可知,Kθ中包含iq2对θd的微分项,无法保证Kθ在动态扰动过程中小于0。因此,在MRR摆臂驱动系统中引入有源阻尼机制,以保证系统动态稳定。MRR摆臂驱动系统有源阻尼控制方法如图4所示。![]() 为MRR摆臂驱动系统给定角速度,其与2号从电动机角速度ωr2的差值Δωr2经比例调节器P,得到2号从电动机给定等效转矩
为MRR摆臂驱动系统给定角速度,其与2号从电动机角速度ωr2的差值Δωr2经比例调节器P,得到2号从电动机给定等效转矩![]() 结合双电动机角度误差θd确定需向2号从电动机注入的阻尼电流
结合双电动机角度误差θd确定需向2号从电动机注入的阻尼电流![]() 与最大转矩电流比电流
与最大转矩电流比电流![]() 相加,即可得到系统给定电流d轴分量
相加,即可得到系统给定电流d轴分量![]() 需要注意的是
需要注意的是![]() 仅在MRR摆臂驱动系统双电动机负载不平衡时出现,待系统重新回归稳态后
仅在MRR摆臂驱动系统双电动机负载不平衡时出现,待系统重新回归稳态后![]() 将逐步趋近于0,且趋近速率及稳态收敛效果由比例调节器P控制。
将逐步趋近于0,且趋近速率及稳态收敛效果由比例调节器P控制。
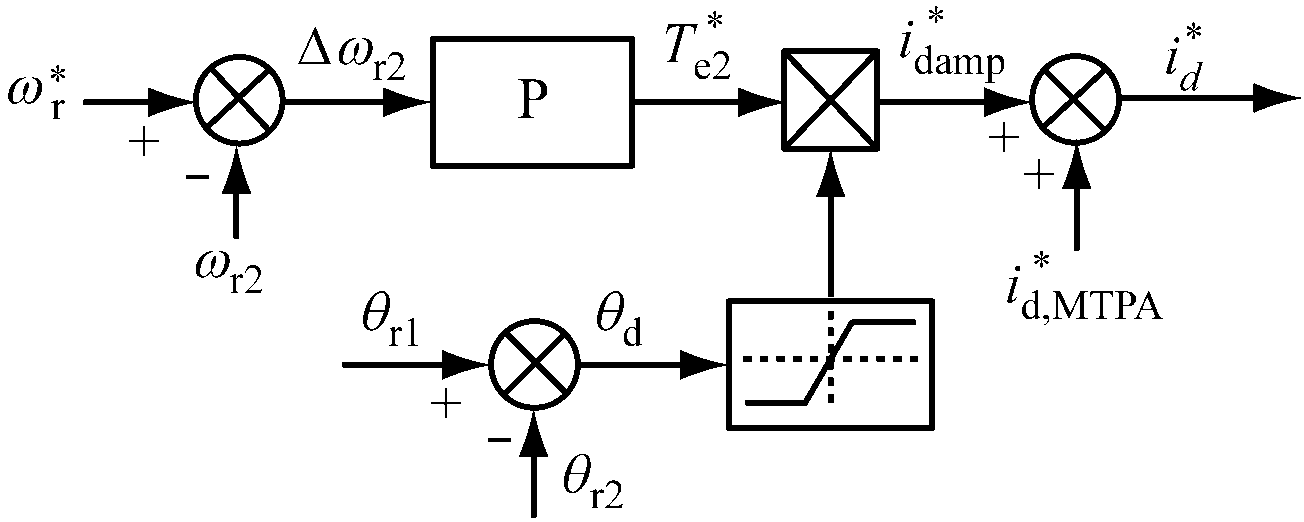
图4 MRR摆臂驱动系统有源阻尼控制方法
Fig.4 Active damping control method of MRR swing arm driving system
MRR摆臂驱动系统样机如图5所示。电动机参数与第2节中一致。控制电路采用ARM+FPGA结构,可实现MRR摆臂驱动系统控制、与上位机多端口通信、驱动保护功能,并可以光纤触发形式输出PWM波形。

图5 MRR摆臂驱动系统样机
Fig.5 Prototype of MRR swing arm driving system
MRR摆臂驱动系统平衡控制模型如图6所示。其包括加权模型状态观测器、主电动机控制环节、有源阻尼控制环节、SVPWM(Space Vector Pulse Width Modulation, 空间矢量脉宽调制)环节4个部分。id,iq为系统电流d轴、q轴分量![]() 为系统给定电流d轴、q轴分量
为系统给定电流d轴、q轴分量![]() 为系统给定电压d轴、q轴分量。
为系统给定电压d轴、q轴分量。
MRR摆臂驱动系统稳态实验结果如图7所示。1号主电动机a相电流ia1幅值较大,约为25 A。2号从电动机a相电流ia2幅值较小,约为8 A,二者频率均为50 Hz。可见在单逆变器驱动下,MRR摆臂驱动系统双电动机电流幅值不同、频率一致,即可在负载不平衡状态下运行于同一转速。1号主电动机电流d轴分量id1=10 A,2号从电动机电流d轴分量id2=0,可见在稳态情况下,id1不为0,其调节得到的10 A电流用于完成对2号从电动机的转矩控制。
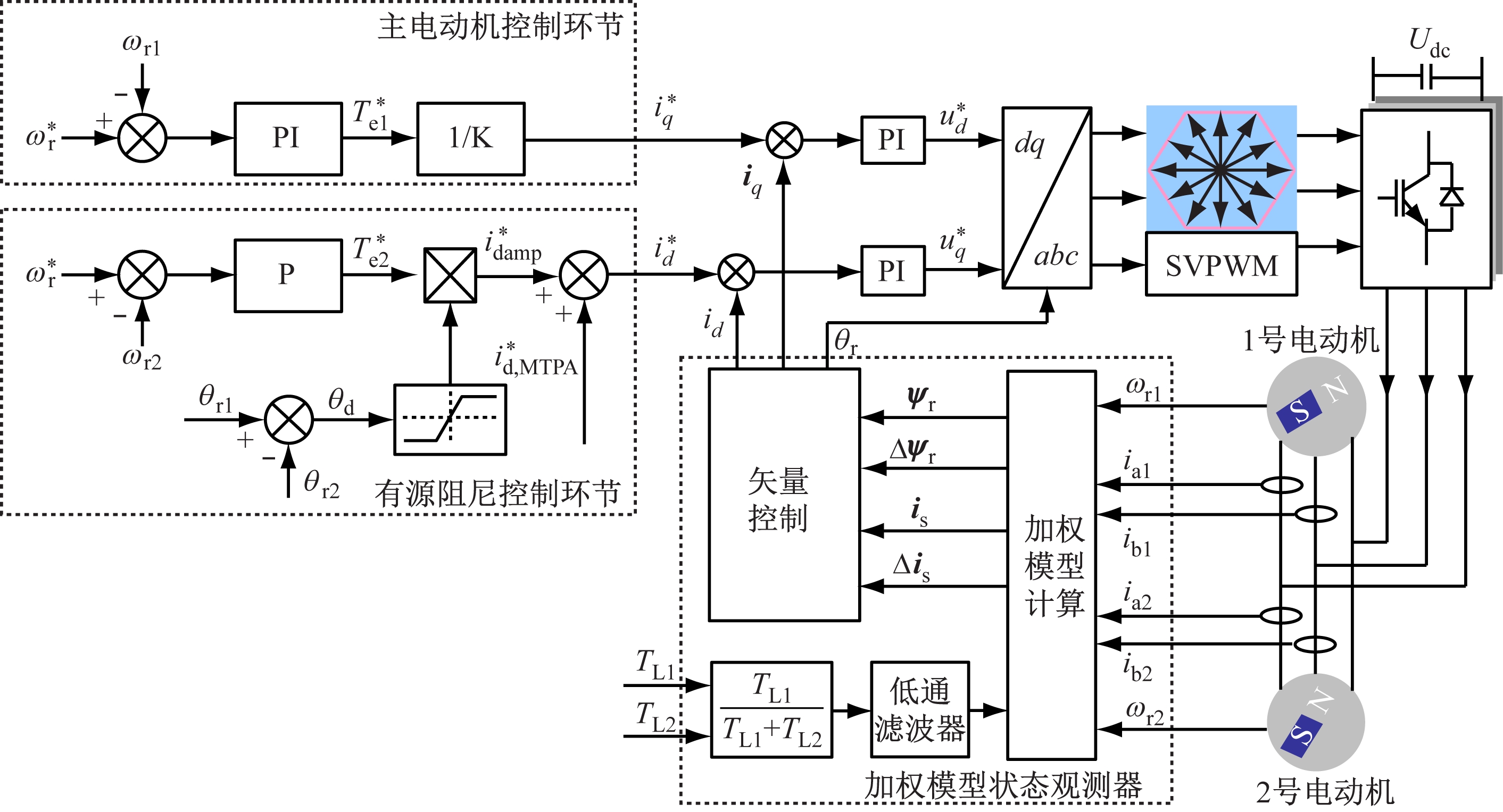
图6 MRR摆臂驱动系统平衡控制模型
Fig.6 Balancing control model of MRR swing arm driving system
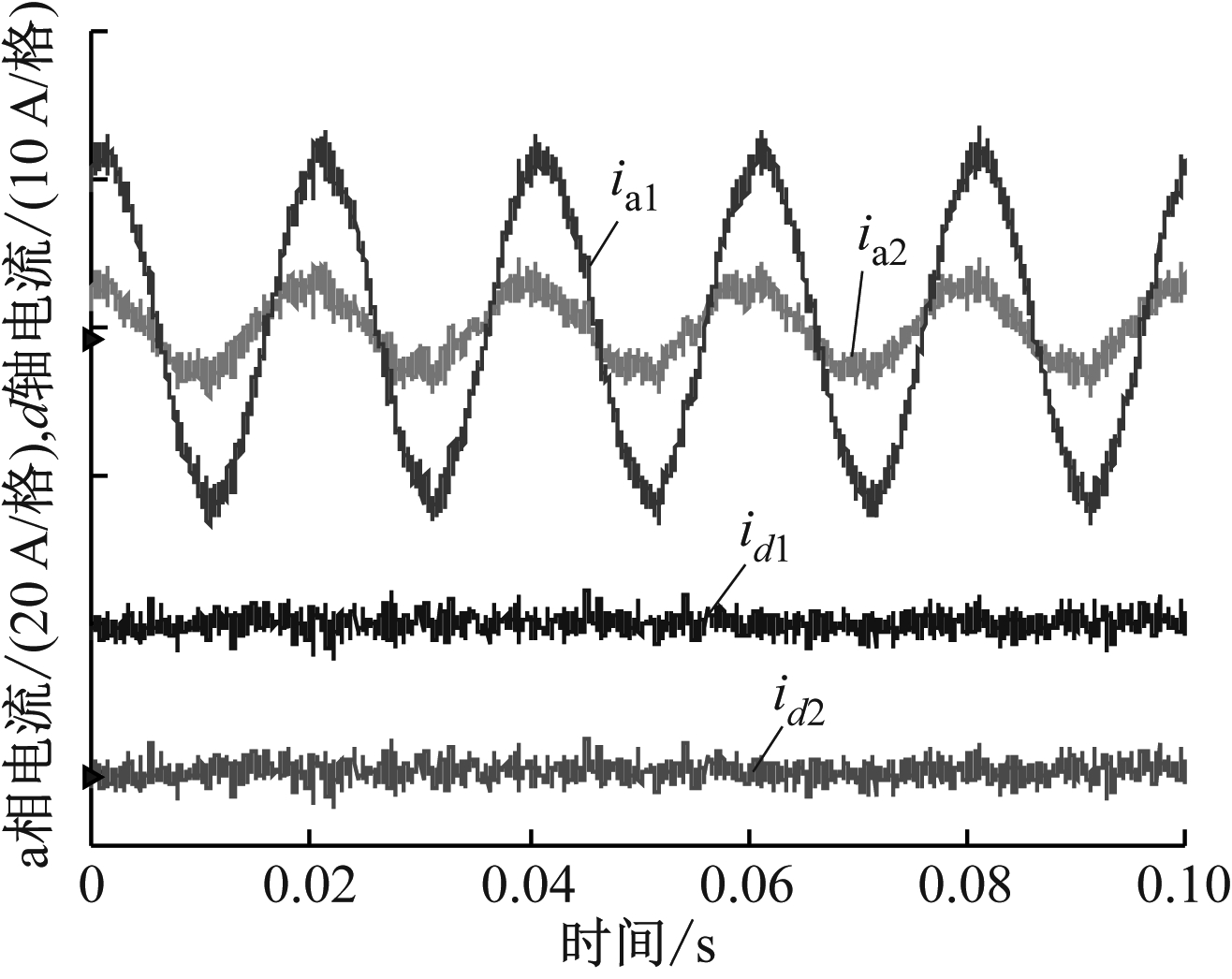
图7 MRR摆臂驱动系统稳态实验结果
Fig.7 Steady state experiment result of MRR swing arm driving system
MRR摆臂驱动系统动态实验结果如图8所示。1号主电动机保持空载特性不变,2号从电动机输出转矩Te2在0.5 s时由0突增为20 N·m。可看出,未采用有源阻尼控制方法时,Te2突变会引起2号从电动机角速度ωr2、1号主电动机电流d轴分量id1出现大幅度多周期振荡。虽然MRR摆臂驱动系统自身的阻尼特性最终可使Te2稳定,但是振荡周期过长(10个基波周期以上),造成MRR摆臂驱动系统动态失稳。采取有源阻尼控制方法后,Te2突变后,ωr2,id1收敛时间更短,扰动持续时间小于0.1 s(1~2个基波周期)。可见有源阻尼控制方法可有效提高MRR摆臂驱动系统的动态收敛特性。
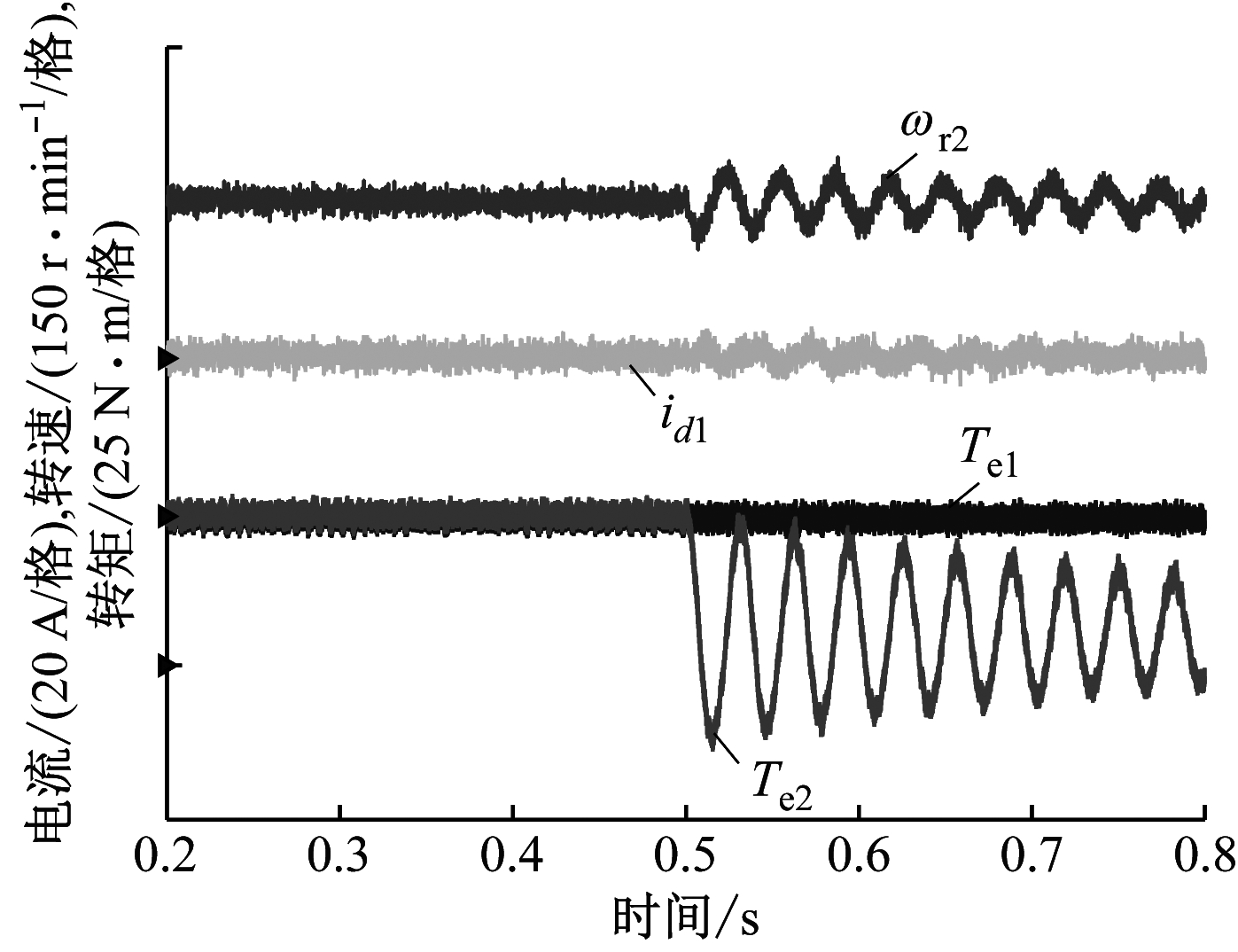
(a) 未采用有源阻尼控制方法

(b) 采用有源阻尼控制方法
图8 MRR摆臂驱动系统动态实验结果
Fig.8 Dynamic state experiment result of MRR swing arm driving system
采用单逆变器驱动双电动机形式设计了一种MRR摆臂驱动系统,并针对该系统负载不匹配问题,提出了一种基于有源阻尼机制的系统平衡控制方法。实验结果表明,MRR摆臂驱动系统的双电动机电流存在交叉耦合关系,通过向从电动机注入阻尼电流,可在不改变主电动机输出转矩的情况下,实现对从电动机输出转矩的有效控制; MRR摆臂驱动系统有源阻尼控制方法引入动态阻尼分量,对于提升MRR摆臂驱动系统动态转矩平衡能力具有积极意义,在相同负载扰动情况下缩短了转矩收敛时间。
参考文献(References):
[1] 田丰,方海峰,李允旺.矿井救灾机器人能量效率模型研究[J].工矿自动化,2014,40(10):15-18.
TIAN Feng, FANG Haifeng, LI Yunwang.Research of self-location method of mine rescue robot[J].Industry and Mine Automation,2014,40(10):15-18.
[2] 蔡李花,方海峰,李允旺,等.矿井救灾机器人自主定位方法研究[J].工矿自动化,2015,41(7): 62-67.
CAI Lihuan, FANG Haifeng, LI Yunwang, et al. Research of energy efficiency model of mine rescue robot[J]. Industry and Mine Automation,2015,41(7):62-67.
[3] GROSSMAN L. Rescue robots could help in next Turkey mine disaster[J]. New Scientist, 2014,2970(222):24.
[4] HUANG Q J, NONAMI K. Humanitarian mine detecting six-legged walking robot and hybrid neuro walking control with position/force control[J].Mechatronics,2003,13(8):773-790.
[5] 张志超,郑之增,方海峰,等.矿井救灾机器人的导航定位研究[J].煤矿机械,2008,29(11):41-43.
ZHANG Zhichao, ZHEN Zhizeng, FANG Haifeng, et al. Research on navigation and localization technologies for mine rescue robots[J]. Coal Mine Machinery,2008,29(11):41-43.
[6] MURPHY R R, KRAVITZ J, STOVER S L, et al. Mobile robots in mine rescue and recovery[J]. IEEE Robotics & Automation Magazine, 2009, 16(2):91-103.
[7] 方海峰,葛世荣,李允旺.具有被动摆臂的四履带机器人越障性能分析[J].中国矿业大学学报,2010, 39(5):682-686.
FANG Haifeng, GE Shirong, LI Yunwang. Obstacle performance analysis of four-track robot with compliant swing arms[J]. Journal of China University of Mining and Technology, 2010, 39(5):682-686.
[8] 魏毅龙.煤矿井下探测与搜救机器人机械系统设计与研究[D].徐州:中国矿业大学,2014.
[9] 李辉.煤矿井下救灾机器人立体视觉导航关键技术研究[D].徐州:中国矿业大学,2015.
[10] ZHANG D, GAO Z. Hybrid head mechanism of the groundhog-like mine rescue robot[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(2):460-470.
[11] AOYAMA H, ISHIKAWA K, SEKI J, et al. Development of mine detection robot system[J]. International Journal of Advanced Robotic Systems, 2007,4(2):504-510.
[12] SHANG W, CAO X, MA H, et al. Kinect-based vision system of mine rescue robot for low illuminous environment[J]. Journal of Sensors, 2016, 2016(4):1-9.
[13] 宋先明. 煤矿井下危险区域探测机器人设计与实现[C]//第2届全国煤矿机械与救援装备高层论坛暨新产品技术交流会论文集,大连,2011:119-122.
[14] 薛旭升.煤矿救援机器人无线通信系统及布放装置研究[D].西安:西安科技大学, 2013.
[15] CHEN C, CHAI W, ROTH H. A single frame depth visual gyroscope and its integration for robot navigation and mapping in structured indoor environments[J]. Journal of Intelligent & Robotic Systems,2015,80(3):365-374.
Rescue robot swing arm driving system and its balance control method
LIU Jia, HU Jinzhi
(Department of Mechanical Engineering, Taiyuan Institute of Technology, Taiyuan 030008, China)
Abstract:For limitation of the maximum permitted size and weight, a mine rescue robot(MRR) swing arm driving system was designed by taking a form of single-inverter driving dual-motor. The system model was built by use of weighted sum method, and current relationship of the dual-motor of the model was deduced and analyzed. For inconsistent MRR swing arm loads caused by complicated working conditions in coal mine underground, a balance control method for the system was proposed based on active damping mechanism. The method was tested by use of a 15 kW MRR prototype, and the result shows that the method can realize dynamic matching of torque under condition of inconsistent MRR swing arm loads.
Key words:mine accident; rescue robot; swing arm driving; dual motors driving; balance control; dynamic torque balance; active damping
文章编号:1671-251X(2017)07-0042-06
DOI:10.13272/j.issn.1671-251x.2017.07.009
收稿日期:2017-01-26;
修回日期:2017-05-20;责任编辑:李明。
基金项目:国家自然科学基金资助项目(U1610251)。
作者简介:刘嘉(1982-),男,山西祁县人,讲师,硕士,研究方向为机械创新设计与控制,E-mail:tygy_lj@126.com。
引用格式:刘嘉,胡晋智.救灾机器人摆臂驱动系统及其平衡控制方法[J].工矿自动化,2017,43(7):42-47. LIU Jia,HU Jinzhi.Rescue robot swing arm driving system and its balance control method[J].Industry and Mine Automation,2017,43(7):42-47.
中图分类号:TD67
文献标志码:A 网络出版时间:2017-06-27 16:30
网络出版地址:http://kns.cnki.net/kcms/detail/32.1627.TP.20170627.1630.009.html