图1 LCL型SAPF系统结构
高云广1,2, 宋建成1, 郑丽君1, 江法洋1, 田飞燕1
(1.太原理工大学 煤矿电气设备与智能控制山西省重点实验室, 山西 太原 030024;2.太原科技大学 电子信息工程学院, 山西 太原 030024)
摘要:针对传统电流控制策略存在高稳态精度与快速动态响应的矛盾,提出了一种基于LCL型有源电力滤波器的复合电流控制策略。该控制策略将比例积分控制和重复控制有机结合,在保证动态响应的基础上,利用PI控制器将控制模型补偿为稳定系统,使其在低频段具有良好的控制特性;利用重复控制器校正LCL型滤波器谐振峰和内环的固有相位滞后,实现电网谐波电流的快速跟踪与高精度补偿。实验结果表明,经过并联有源电力滤波器的谐波补偿,电网电流的总谐波失真明显减小,负载变化时并联有源电力滤波器可实现单周期快速响应,验证了所提出的复合电流控制策略的有效性。
关键词:有源电力滤波器; 重复控制; PI控制; LCL滤波器; 频率特性分析
现代电力电子装置广泛应用于工业和许多其他领域,从而导致非线性负载的大量出现。它将不可避免地降低电能质量,并通过公共耦合点向电网注入谐波污染,从而影响到连接电网的其他设备。尤其是在煤矿井下,其恶劣的工作条件、非线性负荷特性和分布式采掘工艺为谐波产生提供了条件。为了改善矿井自动化煤机装备的启动和运行特性,各种非线性变流设备在矿井电网的应用越来越广,但是其固有的开关特征在运行中生成了谐波,使供电电网的电流、电压波形发生畸变,给供电网络造成污染,严重威胁矿井电力设备的安全运行[1]。因此,对可治理矿井电网污染的电力滤波器的研究引起了专家学者的极大关注。
近年来,并联型有源电力滤波器(Shunt Active Power Filter , SAPF)被广泛用来改善矿井电网的电能质量,为了避免SAPF中开关频率附近的谐波叠加到电网中,在电流输出通道通常接入L型、LC型或LCL型滤波器。LCL型滤波器不仅可在保证快速动态响应的情况下有效抑制开关纹波,而且在成本和体积方面也具有优势[2-3],但是LCL型滤波器的应用使控制模型变得较为复杂,同时会引入谐振,增加了电流控制器的设计难度[4]。为了解决上述问题,有关LCL型SAPF系统的诸多控制方案已经被提出,如比例积分(PI)控制[5]、比例谐振(PR)控制[6]、重复控制(RC)和复合控制[7]等。虽然传统的PI控制器具有快速的动态响应,也易于实现,但它跟踪交流指令信号不能实现零稳态误差,特别是对于高次谐波,因此,只适用于复合电流控制或直流侧电压控制[5,7]。重复控制基于内模原理,特别适用于周期信号的跟踪和干扰抑制[7-10],它固有的不足是动态响应过程中有一个基频周期延迟。文献[8]将PI 控制器和重复控制器并联施加于L型APF系统,PI 控制器可以对输出谐波指令误差进行实时调整,改善APF系统的动态性能,重复控制器用来消除周期性跟踪误差,改善APF 系统的稳态补偿精度。
在上述研究的基础上,本文提出了一种基于LCL型有源电力滤波器的复合电流控制策略,旨在通过LCL型滤波器减小SAPF开关纹波,将重复控制与PI控制相结合实现谐波补偿,利用重复内模及其补偿环节抑制LCL型滤波器谐振峰,提升控制器的稳态精度,并增加电流给定前馈环节,突出动态过程的PI调节能力,提高谐波电流跟踪速度。基于控制对象的频率特性进行电流双闭环校正。实验验证了所提控制策略的正确性和有效性。
1.1 SAPF系统结构
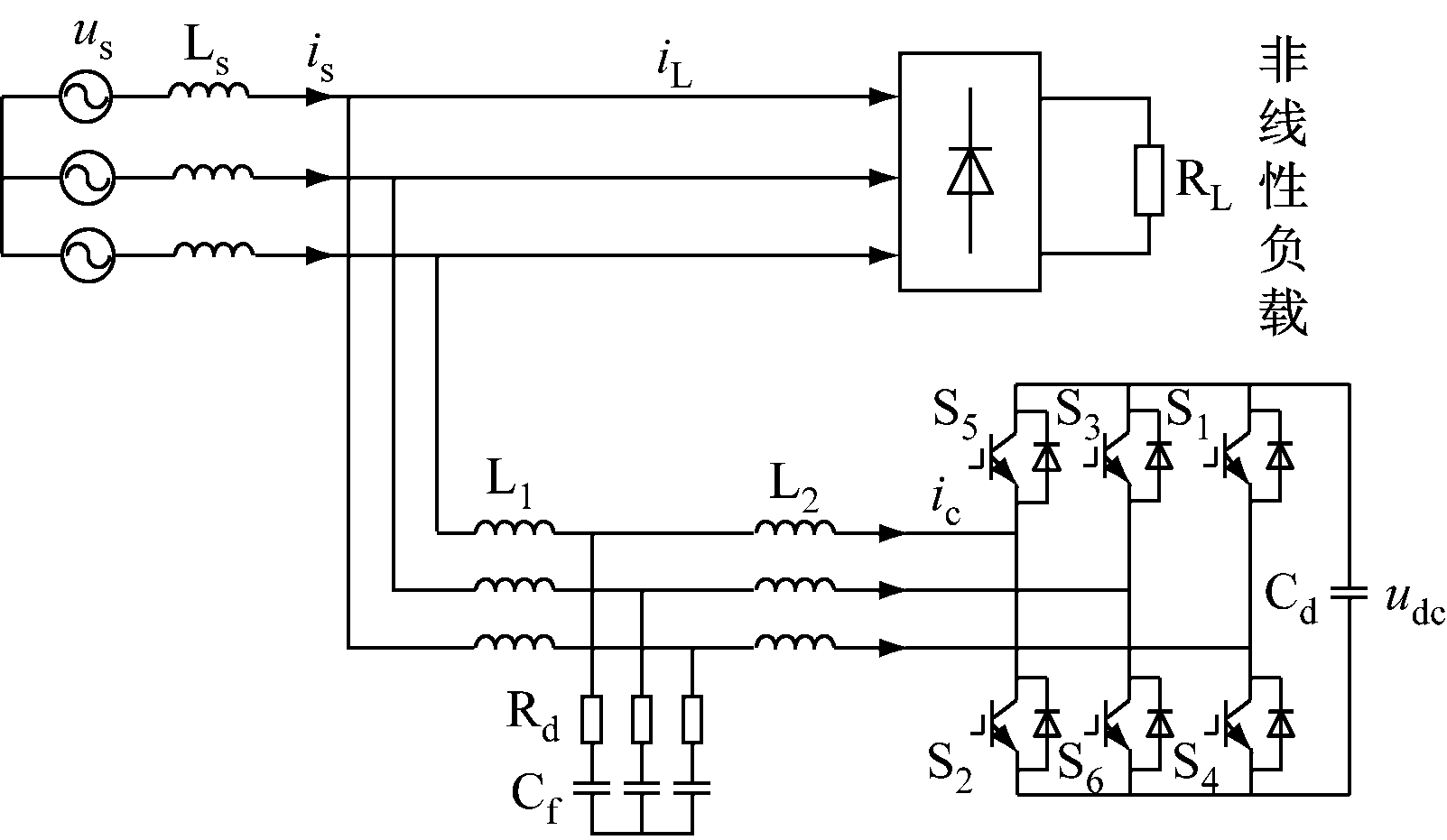
LCL型SAPF系统结构如图1所示。SAPF系统由电压源型逆变器和LCL型输出滤波器串联组成。

图1 LCL型SAPF系统结构
图1中,Ls为电网的等效电感;L1为电网侧电感;L2为逆变器侧电感;Rd为阻尼电阻;Cf为LCL型滤波器的滤波电容;Cd为直流侧储能电容;非线性负载为二极管整流负载;us为电网线电压;udc为直流侧电压;is,iL,ic分别为电网电流、非线性负载电流和SAPF输出电流。
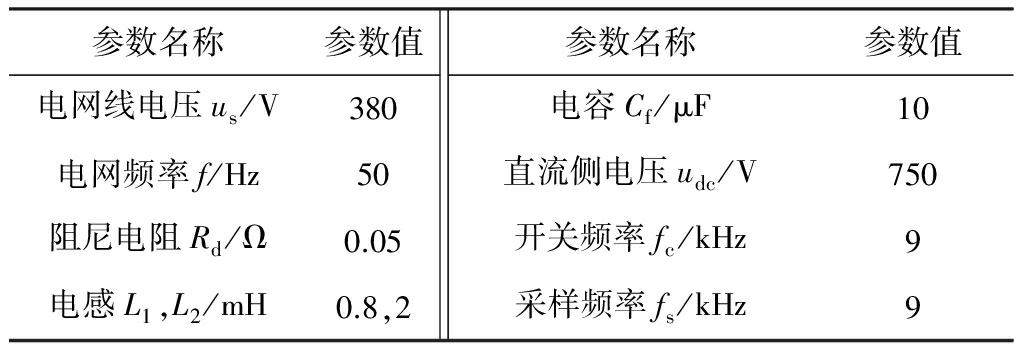
该SAPF通过检测负载电流,计算出谐波指令电流,经过控制器为非线性负荷提供一个补偿谐波电流,使网侧电流输出理想的正弦波。SAPF系统具体参数见表1。
表1 SAPF系统具体参数
1.2 SAPF控制模型
为简化分析,设电网三相对称无畸变,则SAPF每相独立,控制对象在单相等效电路推导。采用瞬时无功功率检测方法,从负载电流iL中提取谐波电流ish,并以电网电流is为反馈量进行闭环跟踪,将SAPF控制成流控电压源uc[11]。图1中,忽略Ls,将iL作为大电网并联非线性负载,其值只与电网电压有关,而与SAPF无关。不考虑iL扰动时[12],基于LCL型有源电力滤波器的单相等效电路如图2所示,其中uc,ic,ics分别为逆变器等效可控电压源、逆变器侧电流和网侧电流。

图2 单相等效电路
由图2可知,当uc单独作用时,可以得出uc到ics的传递函数为
(1)
当us单独作用时,可以得出us到ics的传递函数为
(2)
根据式(1)绘制Gp(s)在S域的Bode图,如图3所示。


图3 Gp(s)在S域的Bode图
由图3可知,Gp(s)中低频段以-20 dB/10倍频斜率衰减,相角滞后90°。在2 200 Hz处,由于振荡环节的作用,出现了一个34.6 dB谐振峰。中频段以-60 dB/10倍频斜率衰减,同时相角滞后扩大为270°。高频段受微分环节的影响,衰减速度逐渐变慢,相角滞后缓慢变小。为了彻底抑制谐振峰,同时将被控对象Gp(s)校正成一个在中低频段零增益、零相移,而在高频段急剧衰减的系统,实现无静差跟踪,需对控制对象Gp(s)进行校正。
本文采用PI控制+重复控制的复合电流控制策略进行谐波电流补偿。PI控制在保证动态响应的基础上,将控制模型补偿为稳定的系统,使其在低频段具有良好的控制特性,同时重复控制校正了LCL型滤波器谐振峰和内环的固有相位滞后,实现了电网谐波电流的快速跟踪与高精度补偿。通过分析频率特性,设计了双闭环电流控制器。外环利用重复控制在周期信号的基频和谐波频率处的极高开环增益特性,保证对周期信号的无静差跟踪[13],实现谐波电流的零稳态误差跟踪;同时通过重复控制器内嵌的补偿器抑制LCL型滤波器谐振峰,但其固有的周期延迟的存在影响到了控制对象的动态响应。为了克服这一控制缺陷,采用内环PI控制器,在低频段改善其低频控制特性,并加快电流控制器的动态响应速度。
2.1 PI控制器设计
内环PI控制框图如图4所示。其中Gp(s)为SAPF系统等效控制对象,Gpi(s)为PI控制器传递函数,SPWM逆变器增益为udc/2。为了与实际数字控制效果更加接近,将图4所示的控制系统离散化,如图5所示。Gpi(z)为利用零阶保持器法离散后的z域的内环PI控制器。由于数字控制本身具有延迟特性,z-1代表数字实现的内在单位延迟。

图4 内环PI控制框图
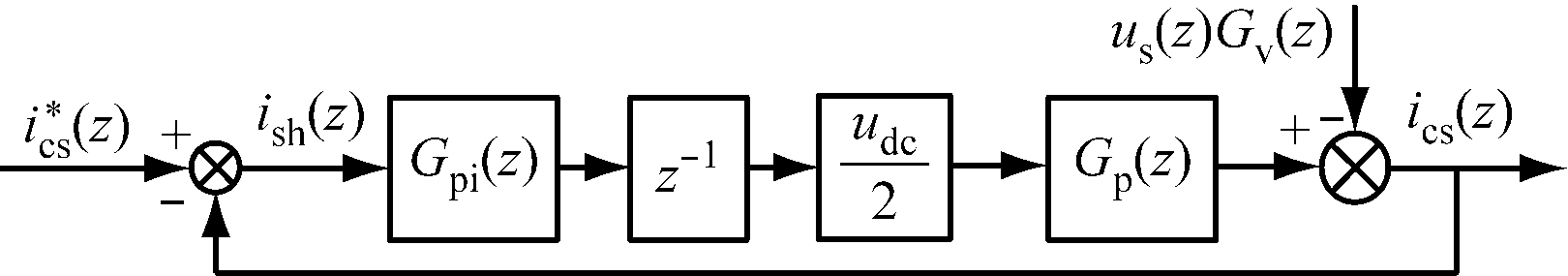
图5 离散化的内环PI控制框图
由图5可得出内环PI控制器的开环传递函数Go(z)和闭环传递函数Gc(z)为
(3)
(4)
采用零极点对消法和实验验算PI参数[14]。经过实验,综合考虑选定KP=0.025,KI=10,则内环的开环和闭环传递函数的Bode图如图6所示。由图6可知,开环频率特性在低频段具有较高增益,实现了电流跟踪,高频段具有较小增益,增强了高频干扰抑制能力,但是在2 200 Hz处依然存在较大谐振峰;闭环频率特性在低频段实现了零相移和零增益,然而在中高频段的相位滞后现象仍然存在,这明显影响了电流控制器的跟踪能力。
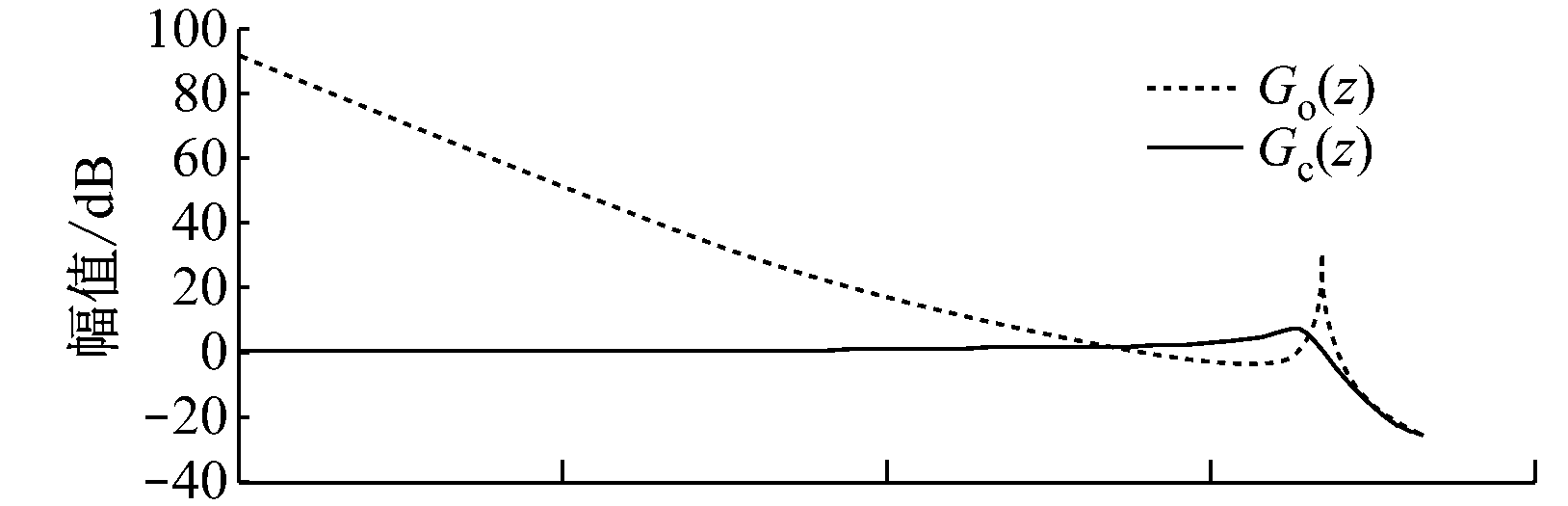

图6 内环的开环和闭环传递函数Bode图
2.2 重复控制器设计
重复外环的设计包括重复控制器内模和补偿器C(z)设计。重复控制器内模中Q(z)选择常数为0.98,采样次数N=fs/f;补偿器C(z)由比例增益kr、超前环节zk和滤波器S(z)构成,外环重复控制器控制框图如图7所示。该结构增加电流给定前馈环节,突出动态过程的PI调节能力,将PI与重复控制完美结合。

图7 外环重复控制器控制框图
补偿器C(z)依据控制对象Gc(z)进行校正设计。补偿后的传递函数C(z)Gc(z)应在中低频具有零相位误差和零增益特性,在高频实现零相移并具有强烈的增益衰减,最终使APF系统具有较强的跟踪能力和抗高频干扰能力。
根据以上分析,滤波器S(z)设计为陷波器F1(z)和二阶低通滤波器F2(z)的组合。零相移陷波器[15]F1(z)的表达式为
(5)
式中m为陷波器F1(z)的阶数,以LCL型滤波器的谐振频率2 200 Hz作为陷波器F1(z)的第1个陷波点来消除谐振峰,计算可得m=2.045,取整后为m=2。
谐波电流控制器的补偿带宽一般为0~2.5 kHz,因此,二阶低通滤波器F2(z)的截止频率和阻尼系数分别等于2.5 kHz和0.707,由S域设计并离散化得到F2(z)为
(6)
zk是一个相位超前环节,用来补偿内环的相位滞后,保证传递函数C(z)Gc(z)零相移,本文中设k=4。比例增益kr可以在电流控制器具有足够的稳定裕度和收敛速度的前提下,通过实验选择一个常数,这里取kr=0.9。
传递函数C(z)Gc(z)的Bode图如图8所示,经过补偿的C(z)Gc(z)在中低频带具有零相位误差和零增益特性,在高频带实现了增益衰减,同时利用陷波器抑制了谐振峰。
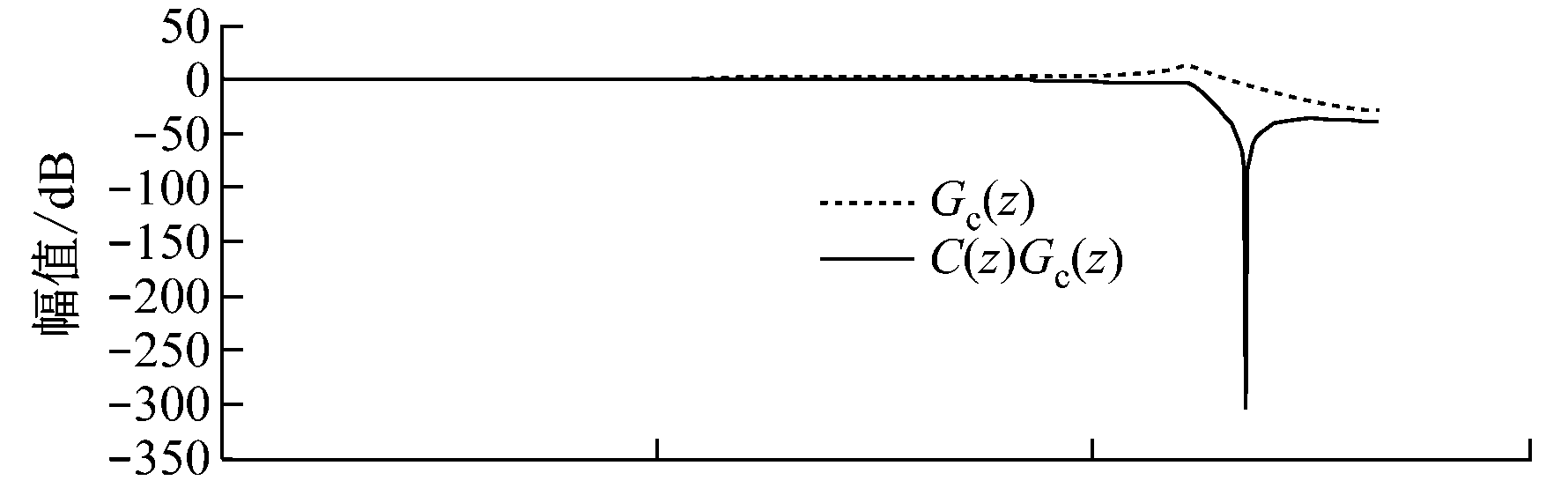
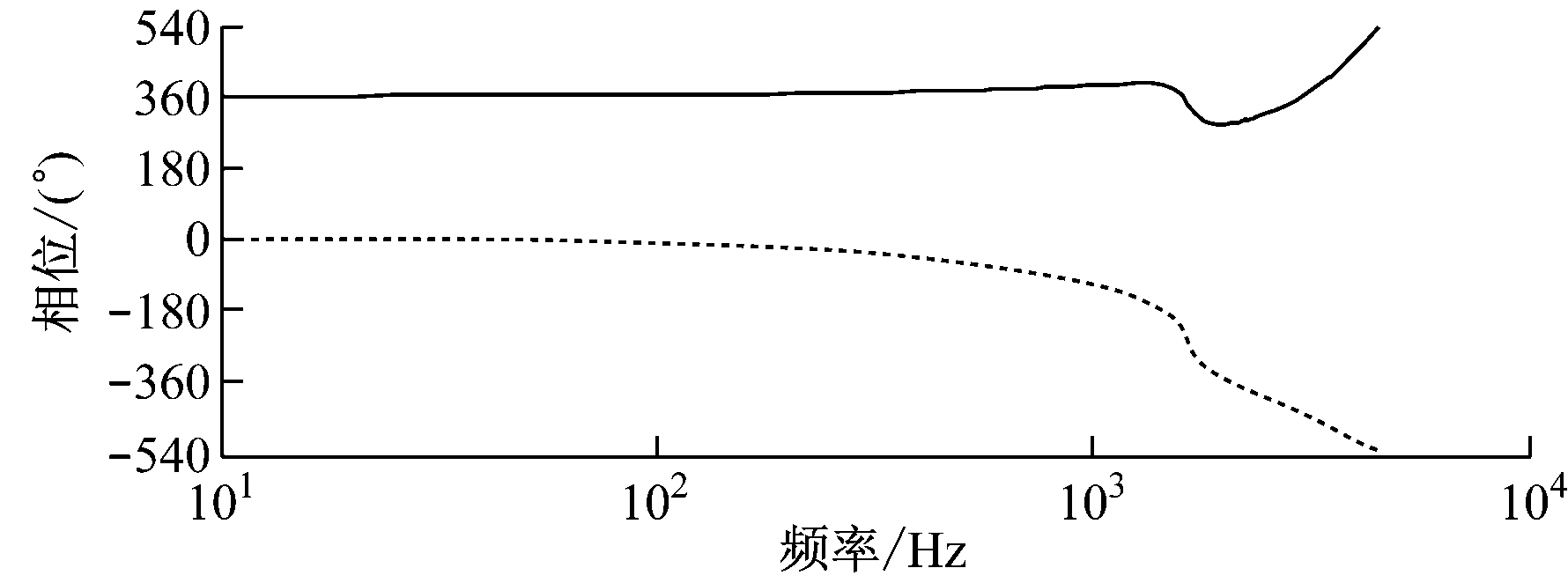
图8 传递函数C(z)Gc(z)与Gc(z)的Bode图
外环的开环传递函数为
(7)
Gop(z)的Bode图如图9所示,在基频及谐波频率处具有较高的增益,高频处增益较低,这正满足前面所述的校正系统的要求,并优化了复合电流控制器的跟踪能力。


图9 开环传递函数Gop(z)的Bode图
2.3 复合控制的双闭环特性分析
由图7所示控制框图可以得出控制器双闭环传递函数为
(8)
式中C(z)=krzkF1(z)F2(z)。
将系统参数及所设计的各环节代入式(8),绘制双闭环传递函数的频率特性曲线,如图10所示。


图10 复合控制系统双闭环传递函数的频率特性曲线
由图10可知,闭环控制系统在中低频段基本上实现了零增益和零相移,高频段具有很强的衰减能力。因此,所设计的双闭环控制系统不仅能很好地跟踪谐波电流,而且可以抑制高频扰动。
为了验证复合电流控制策略的有效性,建立了基于TMS320F28335的LCL型SAPF系统实验平台,进行三相并联型有源电力滤波器谐波补偿实验。
SAPF稳态运行时的电流波形如图11所示。图11(a)为非线性负载电流波形,可以看出,存在较大谐波,经过PI与重复复合控制之后,SAPF输出如图11(b)所示的谐波电流,其对电网电流进行补偿,使电网电流波形基本接近正弦波,如图11(c)所示。

(a) 非线性负载电流波形
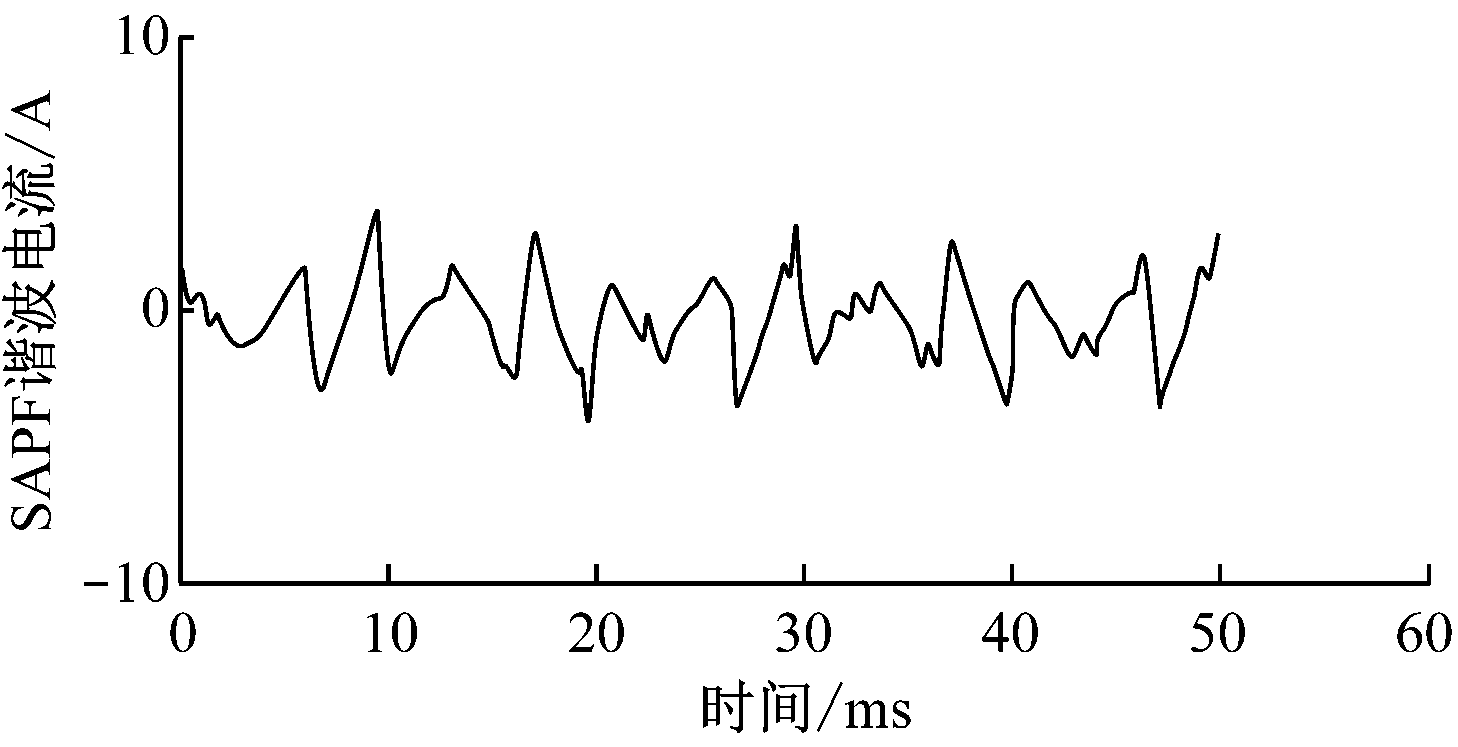
(b) SAPF输出的谐波电流波形
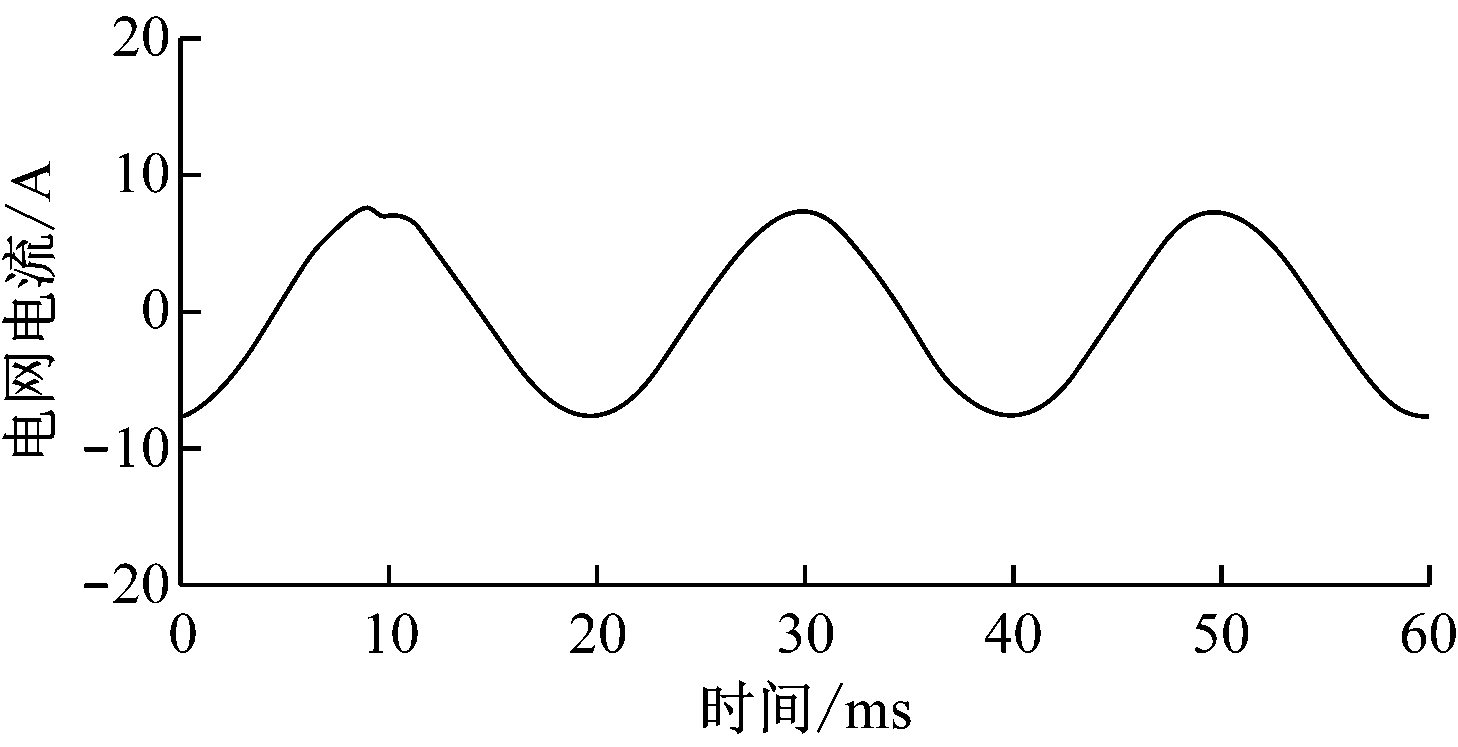
(c) 电网电流波形
图11 SAPF稳态运行时的电流波形
负载电流与电网电流相应的频谱图分别如图12和图13所示。可以看出,投入SAPF之后,第5次、第7次和第11次谐波含量明显减少,这表明电流控制器具有良好的跟踪能力和补偿性能,同时有效抑制了自身开关高频干扰。电网电流总谐波失真从原来的29.5%降低到3.3%,完全符合相关国际谐波标准的规定要求。

图12 负载电流频谱

图13 电网电流频谱
由于矿井电网工况恶劣,SAPF补偿系统不仅要具有良好的稳态跟踪精度,而且要能够快速响应谐波变化。为了验证复合电流控制策略的动态性能,进行了动态加载实验。实验时先使SAPF工作于整流状态,直流侧电压稳定于750 V,瞬时加载实验波形如图14所示。由图14可知,SAPF动态响应时间为1~2个基频周期,电网电流达到稳定,而且补偿效果较好。这主要是因为控制系统中采用了电流前馈的方法,在重复控制外环没有及时跟踪谐波电流时,电流PI内环起主要作用,其快速性的优势体现出来,增强了SAPF系统的动态性能。

(a) 负载电流
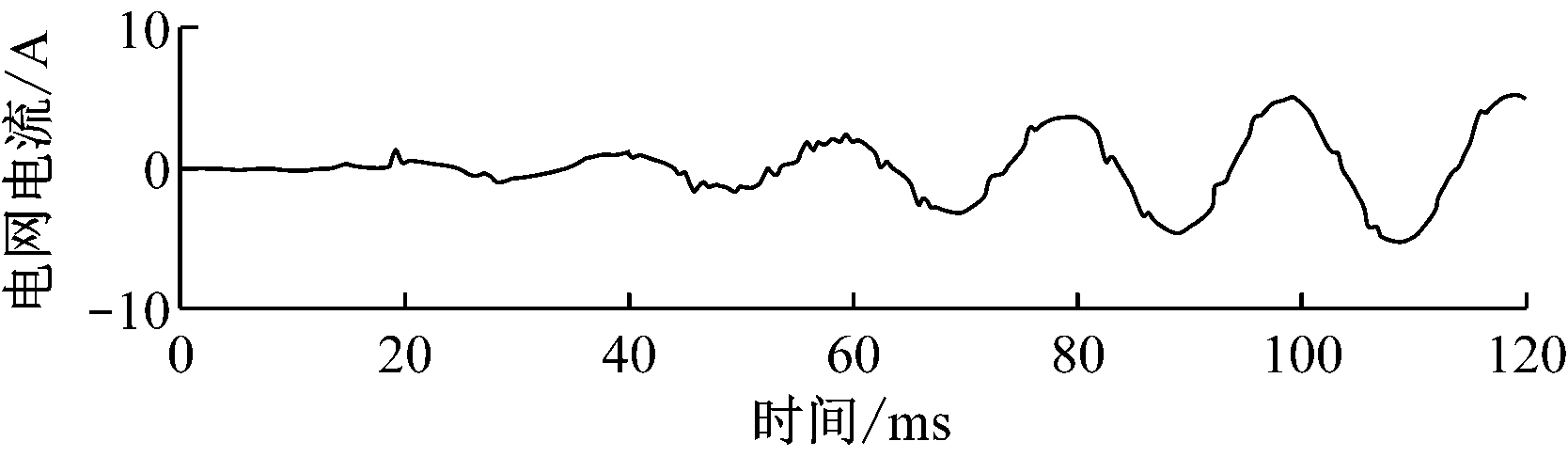
(b) 电网电流
图14 动态加载时负载电流与电网电流波形
基于LCL型并联有源电力滤波器的复合电流控制策略通过PI内环校正使控制对象Gp(s)达到稳定,且在中低频实现零增益和零相移,通过重复控制外环校正进一步提高了SAPF系统高频特性,有效抑制了LCL型滤波器的谐振峰,提高了电流跟踪稳态精度。实验结果表明,该复合电流控制策略实现了电网谐波的稳态精确补偿和动态快速跟踪,当并联型有源电力滤波器接入电网稳定运行时,电网侧电流的总谐波失真从原来的29.5%降低到3.3%;当动态加载时,控制系统动态响应时间为1~2个基频周期。这充分验证了复合控制策略的优
势,在引入电流前馈环节后,控制系统可获得更好的稳态精度和动态特性。
参考文献:
[1] 任子晖.煤矿电网谐波分析与治理[M].徐州:中国矿业大学出版社,2003:1-9.
[2] 许德志,汪飞,阮毅,等.并网接口滤波器拓扑结构推演与分析[J].电工技术学报,2015,30(4):15-25.
[3] 黄秋燕,张阁.基于LCL滤波器的电压型PWM整流器的研究[J].工矿自动化,2011,37(3):39-43.
[4] DANNEHL J,LISERRE M,FUCHS F W.Filter-based active damping of voltage source converters with LCL filter[J].IEEE Transactions on Industrial Electronics,2011,58(8):3623-3633.
[5] 许津铭,谢少军,张斌锋.分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J].中国电机工程学报,2015,35(16):4153-4166.
[6] 易皓,卓放,詹文达,等.用于并联型有源电力滤波器的谐振调节器选择性特性比较分析[J].中国电机工程学报,2014,34(30):5320-5328.
[7] 乔鸣忠,夏益辉,梁京辉,等.基于重复-PI的复合控制应用于并联有源滤波器研究[J].电力系统保护与控制,2013,41(14):54-59.
[8] 王斯然,吕征宇.LCL型并网逆变器中重复控制方法研究[J].中国电机工程学报,2010,30(27):69-75.
[9] 陈玉庆,武玉强,蔡彬.基于电流环复合控制的有源电力滤波器[J].电力自动化设备,2009,29(10):43-49.
[10] ZOU Zhixiang,ZHOU Keliang,WANG Zheng,et al.Frequency adaptive fractional-order repetitive control of shunt active power filters[J].IEEE Transactions on Industrial Electronics,2015,62(3):1659-1668.
[11] LIMONGI L R,DA SILVA F L R,GENU L G B,et al.Transformerless hybrid power filter based on a six-switch two-leg inverter for improved harmonic compensation performance[J].IEEE Transactions on Industrial Electronics,2015,62(1):40-51.
[12] 郭伟峰,徐殿国,武健,等.LCL有源电力滤波器新型控制方法[J].电工技术学报,2010,30(3):42-48.
[13] 竺明哲,叶永强,赵强松,等.抗电网频率波动的重复控制参数设计方法[J].中国电机工程学报,2016,36(14):3858-3867.
[14] 戴金水,吕敬.风力发电并网逆变器双闭环PI调节器的设计[J].电工电气,2011(9):5-9.
[15] 滕国飞,肖国春,张志波,等.采用重复控制的LCL型并网逆变器单闭环电流控制[J].中国电机工程学报,2013,33(24):13-21.
Research on compound current control strategy based on LCL type active power filter
GAO Yunguang1,2, SONG Jiancheng1, ZHENG Lijun1, JIANG Fayang1, TIAN Feiyan1
(1.Shanxi Key Laboratory of Mining Electrical Equipment and Intelligent Control, Taiyuan University of Technology, Taiyuan 030024, China; 2.College of Electronics and Information Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)
Abstract:In view of contradiction between high steady state accuracy and fast dynamic response of traditional current control strategy, a novel compound current control strategy based on LCL type active power filter was proposed. The control strategy combines proportional integral control and repetitive control, the PI controller is used to ensure fast dynamic response, and further compensate control model to the stable system, which has good control characteristics in low frequency range; the repetitive controller is used to correct resonance peak and PI-inner-loop inherent phase lag of LCL filter, so as to realize fast tracking and high precision compensation on harmonic current of the power grid. The experiment results show that total harmonic distortion of the grid current is significantly reduced by compensating of shunt active power filter and the single-cycle fast response is achieved when the load changes, which verifies the compound current control strategy is effective.
Key words:active power filter; repetitive control; PI control; LCL filter; frequency characteristic analysis
文章编号:1671-251X(2017)04-0049-06
DOI:10.13272/j.issn.1671-251x.2017.04.012
收稿日期:2016-09-22;
修回日期:2016-12-07;责任编辑:张强。
基金项目:国家自然科学基金资助项目(5157712);山西省重点实验室开放课题(MEI-201501,MEI-201602)。
作者简介:高云广(1979-),男,山西大同人,讲师,博士研究生,研究方向为电力电子技术,E-mail:gyguangcn@aliyun.com。
中图分类号:TD608
文献标志码:A
网络出版:时间:2017-03-28 17:26
网络出版地址:http://kns.cnki.net/kcms/detail/32.1627.TP.20170328.1726.012.html
高云广,宋建成,郑丽君,等.基于LCL型有源电力滤波器的复合电流控制策略研究[J].工矿自动化,2017,43(4):49-54.