来实现多级胶带的调速。该算法的模糊控制规则基于现场操作人员的经验，具有主观性，一旦控制规则与实际情况不符，那么原调速系统的输出量便会偏大或偏小，造成带式输送机非正常运转，严重的还会导致急停等故障。模糊控制算法不具备自学习能力，模糊控制规则固定不变，而实际的带式输送机运行情况复杂多变，在实际调速系统运行过程中，带式输送机需要根据环境和时间做出不同的调整，所以采用该算法局限性较大，常出现调节速度偏离现有运量的问题。这些问题都直接导致了调速系统的非正常运转，使得其调节速度与期望速度的误差增大。原钢， 李丽宏
(太原理工大学 信息工程学院， 山西 太原 030024)
摘要：针对现有多级胶带调速系统采用二维模糊控制算法存在调节速度与期望速度误差较大的问题，建立了自适应神经模糊推理系统模型，设计了一种基于自适应神经模糊推理系统模型的多级胶带调速系统。该调速系统以第1条胶带的瞬时流量和实时速度为输入量，以变频器的调节频率为输出量实现调速。Matlab仿真结果表明，引入自适应神经模糊推理系统模型的多级胶带调速系统的速度误差可控制在2%以下，运量与带速匹配率得到了优化，对现今煤矿企业的节能减排具有一定的应用价值。
关键词：带式输送机； 多级调速； 自适应神经模糊推理系统; 模糊控制； 节能
带式输送机是目前国内大中型煤矿企业中必不可少的运输设备[1]，多级长胶带联合调速系统(以下简称调速系统)是将2级及2级以上的胶带连接起来，通过对第1条胶带的运量和速度的检测，实现对后续2～i条胶带的速度调节的一种节能调速系统。这种系统主要通过调速来减轻空载和轻载状况下电能的浪费[2]。现有的调速系统多采用二维模糊控制算法，根据现场操作人员的经验生成控制规则，通过输入误差e和误差变化率来实现多级胶带的调速。该算法的模糊控制规则基于现场操作人员的经验，具有主观性，一旦控制规则与实际情况不符，那么原调速系统的输出量便会偏大或偏小，造成带式输送机非正常运转，严重的还会导致急停等故障。模糊控制算法不具备自学习能力，模糊控制规则固定不变，而实际的带式输送机运行情况复杂多变，在实际调速系统运行过程中，带式输送机需要根据环境和时间做出不同的调整，所以采用该算法局限性较大，常出现调节速度偏离现有运量的问题。这些问题都直接导致了调速系统的非正常运转，使得其调节速度与期望速度的误差增大。
针对上述问题，本文建立了自适应神经模糊推理系统(Adaptive Neural Fuzzy Inference System，ANFIS)模型[3],设计了一种基于自适应神经模糊推理系统模型的多级胶带调速系统，以第1条胶带的瞬时流量Q和实时速度v0为输入变量，以变频器的调节频率f为输出变量，通过输出变量来调节第2～i条胶带的带速。ANFIS模型通过对大量实际数据的采集学习、联想、推理计算，在模型内部建立起T-S(Takagi-Sugeno)型模糊推理系统(Fuzzy Inference System，FIS)，采用反向误差传播算法和最小二乘法相结合的“混合法”来对其中的模糊规则和隶属函数参数进行调整，根据对现场数据的学习自动生成if-then形式的模糊控制规则，以此来实现最终的调速，达到带速与运量的匹配调节[4]。
多级胶带调速系统结构如图1所示，该系统由多级胶带级联构成。假设该系统共由i条胶带组成，分别编号为1号，2号，…，i号。系统主要分为3个部分：控制器、检测装置和执行器。其中控制器采用PLC来实现对整个系统的调节控制，PLC一方面用来控制各条胶带的启停，另一方面通过串口线与上位机相连[5]，接收上位机的指令，根据上位机中ANFIS模型运算产生的调节频率对变频器频率进行调节。检测装置分为托辊式带速检测传感器和电子胶带秤，其中托辊式带速检测传感器用来测量第1条及第2～i条胶带的实时速度，并将其发送到PLC中;电子胶带秤只安装在第1条胶带上，用来测量不同时刻系统的瞬时流量Q;称重仪表将接收到的称重信号进行滤波处理后，经过串行通信将所测数据传入到上位机中进行处理。执行器由变频器和电动机组成，是速度调节的直接控制单位。
图1 多级胶带调速系统结构
本文将已经训练好的ANFIS模型传入上位机中替换原有系统中的人工模糊控制规则表。系统将不同时刻测量所得的第1条胶带的实时速度v0和瞬时流量Q传入上位机，与上位机中所存的最佳匹配带速对比，如果达到最佳，则不对第2～i条胶带的带速作调整;否则将这2个变量输入到ANFIS模型[6]中，ANFIS模型根据这2个输入量输出一个对应的调节频率f，然后PLC将命令下发到执行器中实现控制，最终的调节速度即为该运量下的优化匹配速度。系统工作流程如图2所示。
模糊控制[7]是一种基于操作经验总结出的用自然语言表述的控制策略，它的设计不依赖于被控对象的精确数学模型，易于被操作人员接受。但模糊控制不能将人类的知识经验自动转换为推理规则库，隶属函数和控制规则容易出现主观性偏差，缺乏有效的方法优化隶属函数参数以减小输出误差和提
图2 系统工作流程
高性能指标。ANFIS是由Jang Roger提出的将神经网络的学习机制引入模糊系统所构成的带有人类感知成分的自适应系统，它兼顾神经网络的非线性、自适应性和模糊推理系统处理复杂问题的优势。典型的ANFIS模型结构如图3所示。
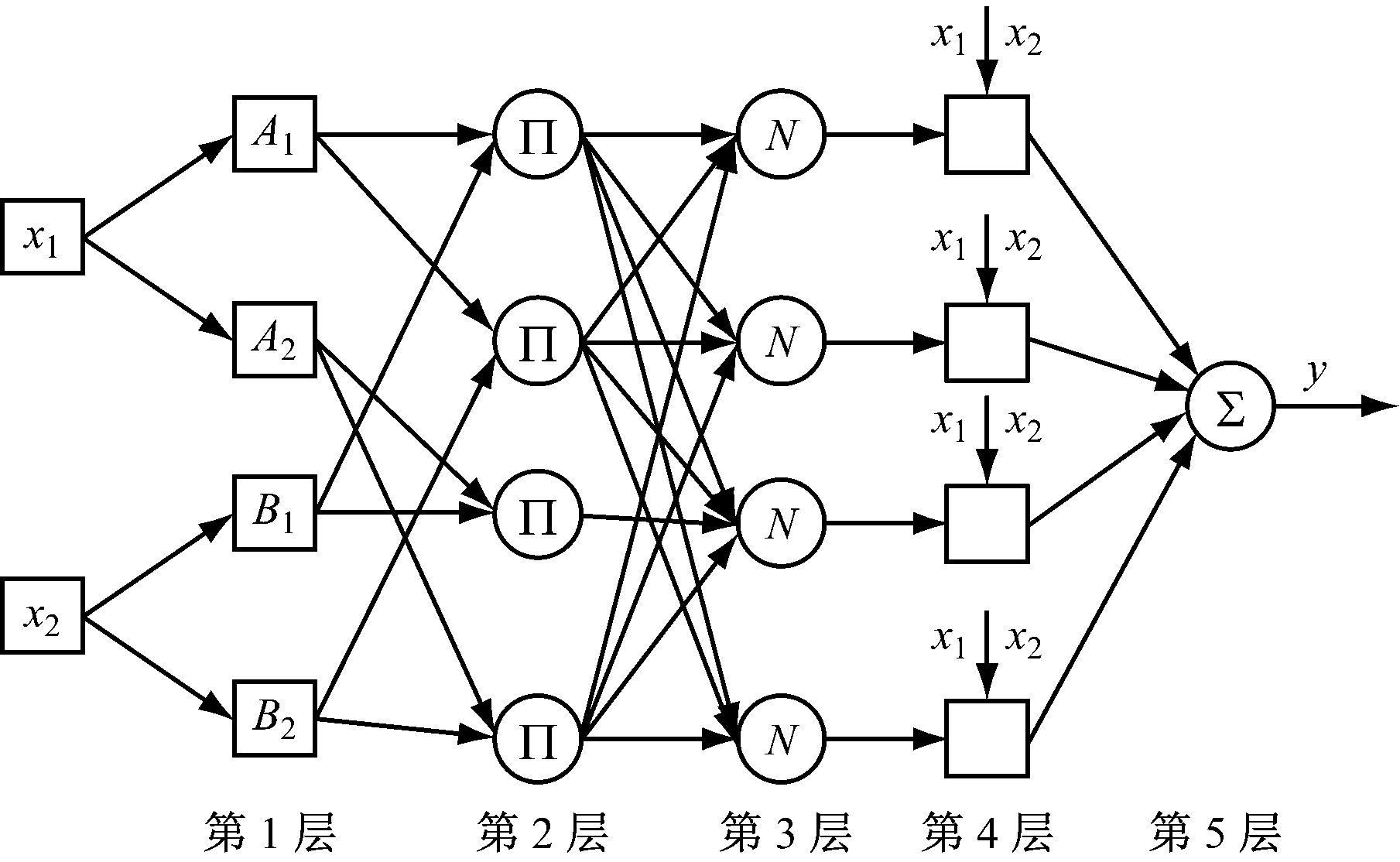
图3 典型的ANFIS模型结构
图3所示的ANFIS模型为双输入单输出模型，网络结构分为5层，从左往右依次为模糊化层、规则推理层、归一化层、逆模糊化层和输出层。其中x1,x2为输入变量；第1层中的Ai,Bi(i=1,2)分别为x1,x2模糊化后所得变量；第2层中的Π代表模糊规则；第3层中的N代表归一化结构；y为输出变量。上述典型结构的规则库由以下4条规则组成，其中{pi,qi，ri}为其输出的一阶数值函数参数：
Rule 1:ifx1isA1andx2isB1, theny=p1x1+q1x2+r1
Rule 2: ifx1isA2andx2isB2,theny=p2x1+q2x2+r2
Rule 3: ifx1isA3andx2isB3,theny=p3x1+q3x2+r3
Rule 4: ifx1isA4andx2isB4,theny=p4x1+q4x2+r4
调速系统的ANFIS模型设计流程如图4所示。
(1) 确定模型结构：建立ANFIS模型时，首先要假设一个参数化的模型结构，即建立一个初始模糊系统。ANFIS模型中所包含的初始模糊系统类型为一阶T-S型模糊推理系统。要确定初始模糊系统的结构，需要先确定输入输出变量和初始隶属函数。输入输出变量的确定：输入变量为瞬时流量Q和带速v0，论域分别为[600，1 500]和[0.5，2]；输出变量为频率f，论域为[16,60]。将2个输入变量的模糊子集都选取为7个，每一个模糊子集对应的初始隶属函数都选取为高斯函数(gaussmf)[8-9]，其表达式为
图4 调速系统ANFIS模型设计流程
(1)
式中：σ,c为位置参数,σ决定曲线的宽度；c决定函数中心的位置。
(2) 导入训练数据：采集匹配率高的数据作为ANFIS模型的初始训练样本并导入ANFIS模型，选取瞬时流量Q为600～1 500 t/h时相对应的均匀分布的带速v0和频率f并导入ANFIS模型。
(3) 选取训练算法：在该调速系统运用的ANFIS模型中，选取了“Hybrid”(混合法)来进行训练，该算法结合了误差反传播(Back Propagation)学习算法即BP算法和最小二乘法。调速系统中的ANFIS模型结构如图5所示。
图5 调速系统中的ANFIS模型结构
观察图5可以发现,该调速系统中的ANFIS模型和典型的ANFIS模型结构相比，没有了逆模糊化层，只有4层节点[10]。这是因为本次设计采用了T-S型初始化模糊系统，输出量为一阶线性函数，是清晰量,不需要逆模糊化，所以,该系统的网络结构共有4层，每层的节点数分别为14,49,49,1，此处输入变量为Q和v0，输出为f，用O1·i表示第1层第i个节点的输出，依此类推。每层节点的作用具体分析如下：
第1层：该层为模糊化层，本层节点将输入信号模糊化：
(2)
式中:Ai和Bj为模糊子集；μAi,μBj为模糊集的隶属函数，此处为高斯函数，其表达式为
(3)
这里的[σi,ci]称为前提参数，隶属函数的形状及拐点随着这些参数的变化而改变。
第2层：该层为规则推理层，本层节点用于计算各条规则的适用度ωi，即将各输入信号的隶属函数相乘，并将乘积作为本规则的适用度。
(4)
第3层：该层为归一化层，本层节点进行各条规则适用度的归一化计算，即计算第i条规则的适用度ωi与全部规则的适用度之和∑ωi的比值。
(5)
第4层：该层为输出层，本层为单节点，本层节点用于计算各条规则的输出并进行汇总,得出该系统的总输出。
各条规则的输出如下：
(6)
这里的{pi,qi，ri}称为结论参数。
系统的总输出如下：
(7)
在该系统采用的ANFIS模型结构中，给定前提参数后，ANFIS的输出可以表示成结论参数的线性组合：
f=
(8)
混合学习算法在该结构中的具体作用：① 确定前提参数的初始值后运用最小二乘法计算结论参数。② 根据结论参数进行误差计算，然后采用前馈神经网络中的BP算法将误差由输出端反向传到输入端，用梯度下降法更新前提参数，从而改变隶属函数的形状。
由式(8)得
(9)
式中列向量X构成结论参数集合{p1,q1,r1，…，p7,q7,r7}。
若已有P组输入输出数据对，且给定前提参数，则矩阵A,X,f的位数分别为P×21，21×1和P×1。一般的，样本数据的个数远大于未知参数的个数(P>>21),使用最小二乘法可以得到均方误差最小
)意义下的结论向量的最佳估计X*,即
(10)
(4) 训练ANFIS模型：检测是否达到事先设定的精度要求，由此判断下一步动作。另外，ANFIS模型[11]中的模糊控制的参数规则可以随时通过数据的训练来优化，使得该调速系统具有了自学习能力，而原有的二维模糊控制算法是根据人工经验所得的控制表进行调节的，模糊控制规则表固定不变，因此，采用ANFIS模型的调速系统避免了不同时节规律对调速系统精确度的干扰。
Matlab的Simulink Library Browser(仿真模块库)中设有专用的模糊逻辑工具箱(Fuzzy Logic Toolbox),可以方便地设计模糊推理系统,进行模糊推理仿真。此外，Matlab还提供了ANFIS模型工具箱函数和图形化编辑工具，能够用神经网络对大量已知数据进行学习、联想和推理计算，从而建立起T-S型FIS。
根据第2节中所述步骤建立ANFIS模型，确定T-S型FIS的规则和隶属函数，最终给出输出变量的表达式，模型训练完成后便可以将其运用在调速系统的上位机中实现调速。将50组数据作为神经网络的训练样本，10组数据作为测试样本，每一组数据均由输入变量(1号胶带瞬时流量Q，1号胶带速度v0)和输出变量(调节频率f)组成。ANFIS模型参数设置：FIS生成方式为Grid partition； 输入变量的MF(隶属函数)个数为[7,7]；输入MF类型为gaussmf； 输出MF类型为Linear；优化方法为hybrid；误差容限为0；训练次数为50。
(1) 在Matlab的ANFIS工具箱中载入训练数据和测试数据,得到如图6所示的散点图。
图6 数据散点图
(2) 采用网格分割法(Grid Partition)生成初始化FIS。
(3) 采用“Hybrid”(混合法)训练神经网络，选取训练次数为50次，最终得到的误差如图7所示。误差为0.197 2，即0.2%左右，说明训练具有良好的效果。
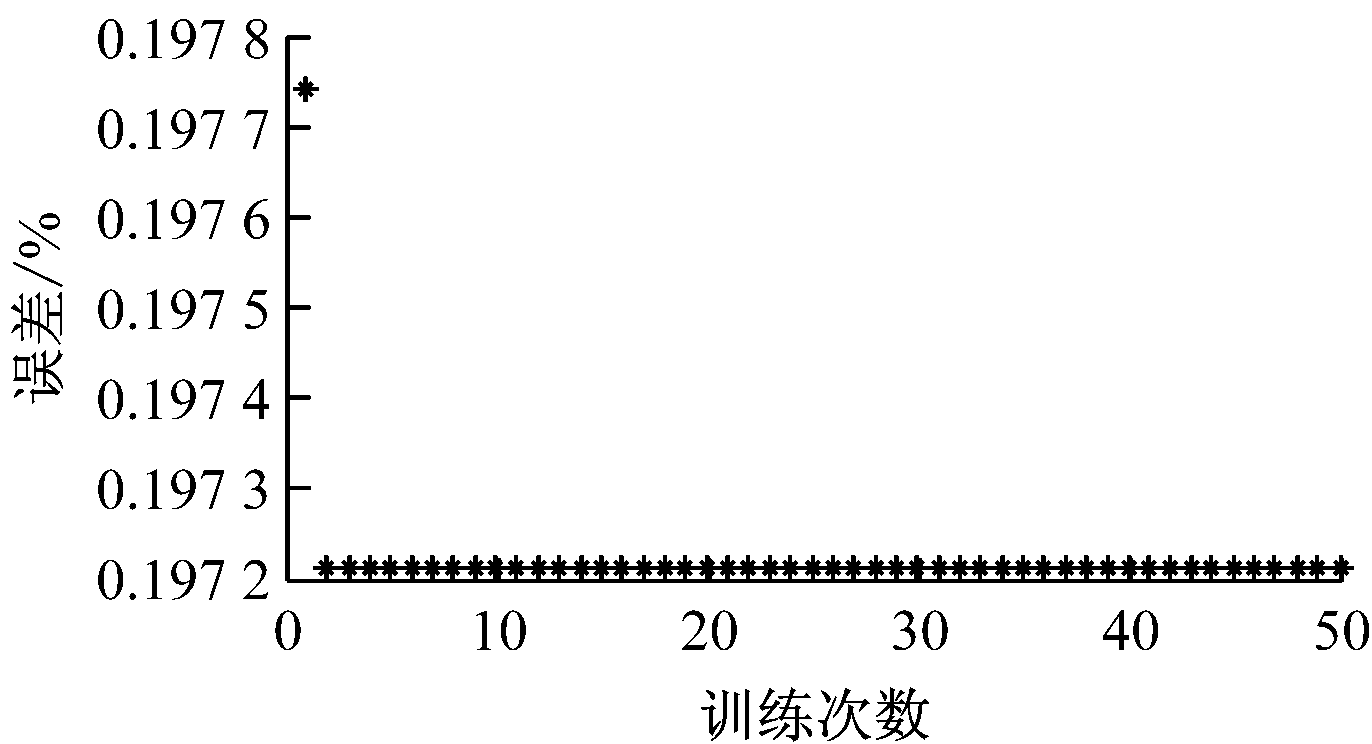
图7 训练误差曲线
(4) 生成最终的FIS，其最终的空间曲线关系如图8所示。空间曲线的曲面越光滑、平缓，该系统的性能越好。本次仿真得出的曲面基本处于平滑状态，说明训练效果理想。
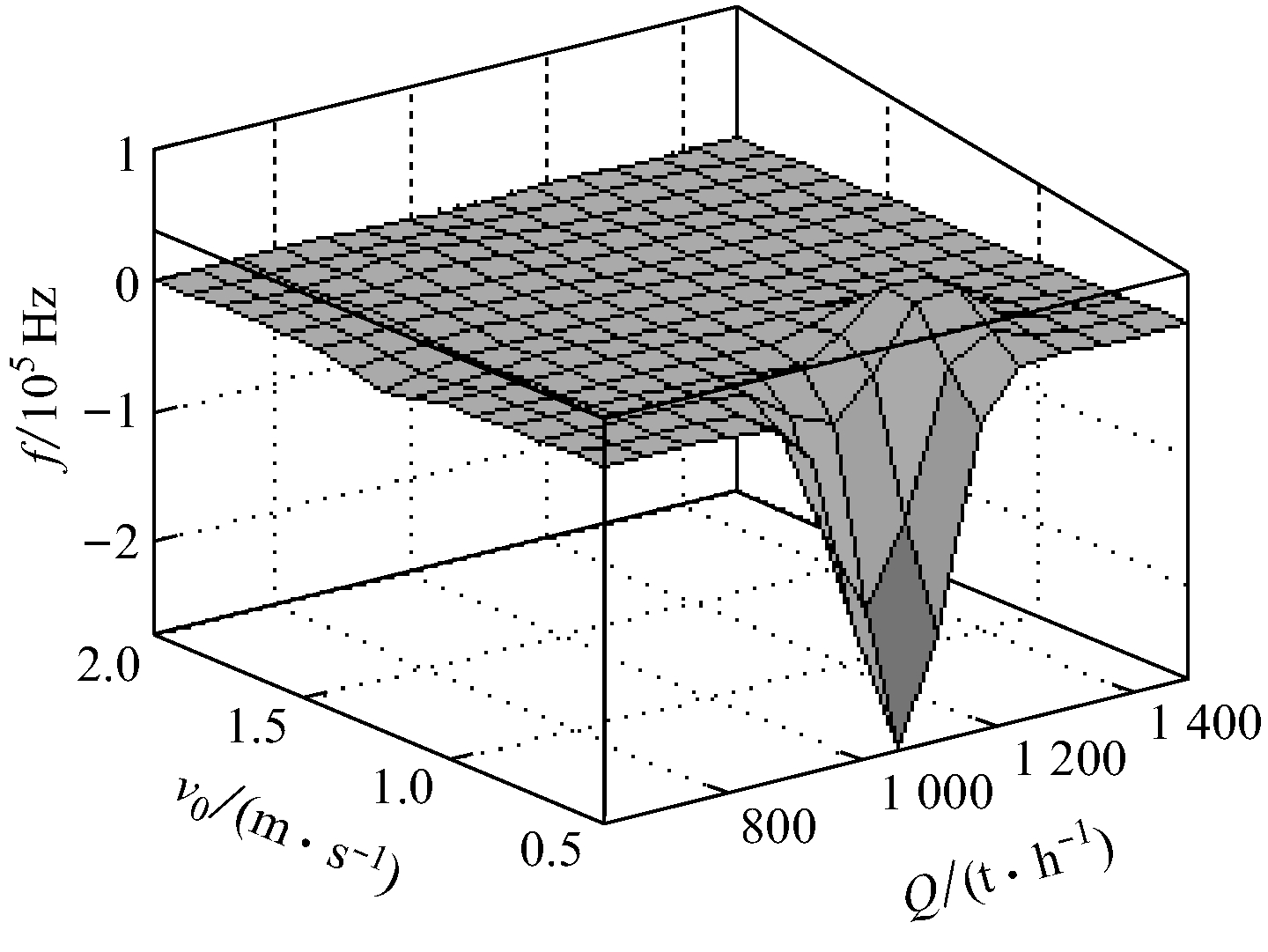
图8 二维模糊控制系统的空间关系曲线
分别选取7组隶属函数，最终生成7×7=49组模糊规则。该仿真通过对数据的训练自动生成模糊规则,现随机抽取3组进行说明,见表1。
模糊规则前标号是模糊规则的序号，查阅Matlab中经过神经网络训练后的参数，分别得出这3条规则下的输出函数为
表1 模糊规则
(11)
可以看到，通过此次仿真，确定了各个输出函数的结论参数{pi,qi,ri}，将生成的模型载入上位机中，调速系统即可根据模型进行调速。
为了验证最终效果，在山西古交某中型煤矿选取了有级联关系的4条胶带进行测试，其在厂内的编号分别为101,112,113,115。其级联关系如图9所示。各条胶带的规格参数见表2。
图9 某煤矿4条胶带的级联关系
表2 各条胶带的规格参数
采集一天中不同时刻的10组数据来进行验证，分别采集瞬时流量Q,第101号(第1级)胶带的带速v0，将其传入上位机中已经训练好的ANFIS模型，得出其余各条胶带的调节频率f，由上位机将此频率传给控制器PLC[12]，再由PLC控制编号为112,113,115的各条胶带的执行器实现调速。将调节后的速度与此刻运量匹配的最佳速度vb对比,得出误差,见表3。从表3可看出，误差在2%以下。
采用人工经验二维模糊控制的调速系统与采用ANFIS模型的调速系统的调节速度的误差率对比见表4。从表4可以看出,采用ANFIS模型后,系统误差减小了0.4%以上。
表3 速度误差
表4 误差率对比
经过ANFIS模型运算得出的速度和最佳期望速度的对比曲线如图10所示。由图10可以直观地看出,输出的调节速度曲线与最佳速度曲线基本重合,说明采用ANFIS模型的调速系统的调速性能得以大幅优化。
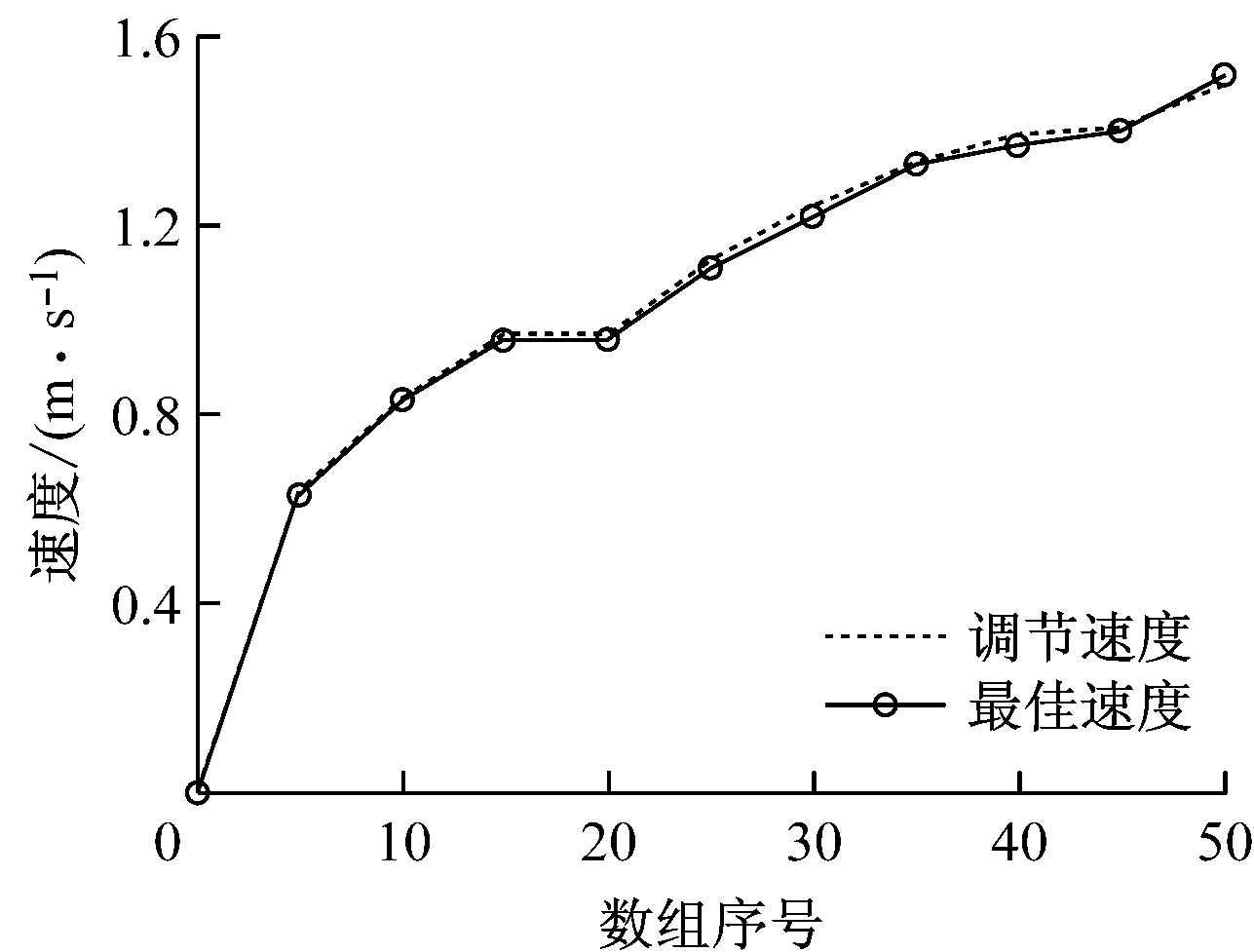
图10 经过ANFIS模型运算得出的速度和最佳期望速度的对比曲线
将ANFIS模型引入到多级胶带调速系统中，采用反向传播法和最小二乘法结合的混合算法对系统输入的数据进行训练，得出相应的模糊控制隶属函数参数和模糊规则，防止了主观性偏差错误的出现。在实际运用中，ANFIS模型可以根据不同数据的规律特征进行新的训练，防止带式输送机的时变性干扰。Matlab仿真结果表明，引入ANFIS模型的调速系统的速度误差控制在2%以下，运量与带速匹配率得到了优化，对现今煤矿企业的节能减排具有一定的应用价值。
参考文献：
[1] 马晓泽.带式输送机集中控制系统改造设计[J].工矿自动化，2012，38(4)：89-91.
[2] 李丽宏，王宏，武丽君.多级长皮带联合调速节能系统的设计[J].软件，2012,33(3)：9-11.
[3] 付雅婷,杨辉. 基于ANFIS模型的高速动车组运行优化控制[J].控制工程,2016(10):1572-1577.
[4] 孙伟，王慧，杨海群.带式输送机变频调速节能控制系统研究[J].工矿自动化，2013，39(4)：98-101.
[5] 邵杰,初学导.基于PLC的模糊控制变频调速系统[J].电气时代,2005,10(1):2-3.
[6] 王艳艳,尹少平,王灵梅,等.基于ANFIS模型的风功率超短期预测研究[J].自动化技术与应用,2016,35(1):17-21.
[7] 李丽宏，王宏，武丽君.模糊控制在多级长皮带联合调速节能系统中的应用[J].软件，2012,33(3):22-24.
[8] 杨辉,朱凡,陆荣秀,张志勇.基于ANFIS模型的Pr/Nd萃取过程预测控制[J].化工学报,2016,67(3):982-990.
[9] 白国振,俞洁皓.基于改进模糊神经网络的PID参数自整定[J].计算机应用研究,2016(11):358-363.
[10] SAXENA N, KUMAR A.Reactive power compensation of an isolated hybrid power system with load interaction using ANFIS tuned STATCOM[J].Frontiers in Energy,2014,8(2):261-268.
[11] 刘千,韩璞,王东风.基于ANFIS模型的烟气含氧量建模和预测[J].计算机仿真,2014(10):437-439.
[12] 刘晶晶.PLC在皮带机自动张紧装置中的应用[J].电工技术,2014(2):40-41.
YUAN Gang， LI Lihong
(College of Information Engineering, Taiyuan University of Technology, Taiyuan 030024, China)
Abstract：In view of problem of big error between adjustment speed and expected speed of existing multistage belt speed-regualtion system adopting two-dimensional fuzzy control algorithm, a kind of adaptive neural fuzzy inference system (ANFIS) model was established, and a multistage belt speed-regualtion system based on ANFIS was designed. The speed-regualtion system takes instantaneous flow and real-time speed of the first belt as input, and takes regulating frequency of frequency converter as output to realize speed control. The Matlab simulation results show that the speed control error of the speed-regualtion system introducing ANFIS model is below 2%, capacity and belt speed matching rate are optimized, which has certain application value for energy saving and emission reduction of coal mine enterprises.
Key words：belt conveyor; multistage speed-regualation; ANFIS; fuzzy control; energy saving
文章编号：1671-251X(2017)01-0042-06
DOI：10.13272/j.issn.1671-251x.2017.01.011
收稿日期：2016-07-28；
修回日期：2016-10-11；责任编辑：张强。
作者简介：原钢(1992-)，男，山西太原人，硕士研究生，研究方向为检测技术与智能仪表，E-mail:steelyuan1@163.com。
中图分类号：TD634
文献标志码：A
网络出版：时间：2016-12-30 10:02
网络出版地址：http://www.cnki.net/kcms/detail/32.1627.TP.20161230.1002.011.html
原钢，李丽宏.一种多级胶带调速系统研究[J].工矿自动化，2017,43(1)：42-47.