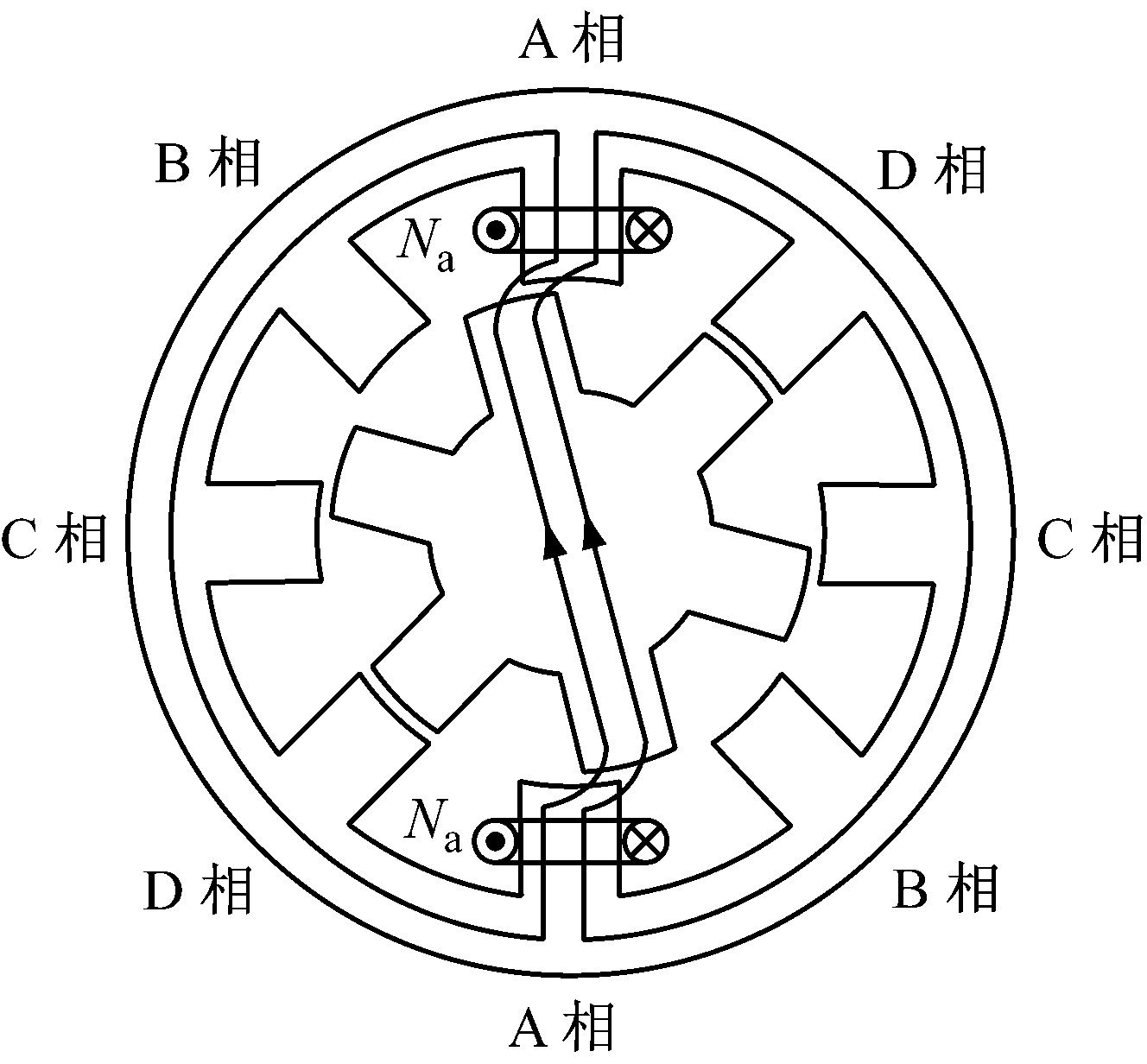
图1 8/6极SRM单相励磁运行原理
肖林京, 李波, 孙传余, 文艺成, 陈忠霞
(山东科技大学 机械电子工程学院, 山东 青岛 266590)
摘要:为研究8/6极开关磁阻电动机转矩输出特性,阐述了开关磁阻电动机单相励磁原理,利用Maxwell 2D有限元软件分析了电动机齿极间气隙处磁路分布,并提出了一种适用于8/6极开关磁阻电动机的新型椭圆磁路模型;在该模型基础上求解气隙磁导,得到了电动机处于平衡位置时的转矩数学模型;最后,通过有限元仿真结果证明了转矩数学模型的正确性。
关键词:开关磁阻电动机; 单相励磁; 数学模型; 磁路分割法; 有限元分析
网络出版地址:http://www.cnki.net/kcms/detail/32.1627.TP.20160405.1133.015.html
开关磁阻电动机[1-2](SRM)因结构简单、工作可靠、几乎无需维护的优点,在多粉尘、强震动的环境中有着更好的适用性;且SRM较一般电动机具有启动力矩大、启动电流小、调速性能好、调速范围宽等优点[3],对煤矿生产设备的性能改进具有重要意义[4],例如提高电牵引采煤机的负载均衡性能、矿井提升机的速度控制性能,以及解决矿用绞车和带式输送机的电网冲击问题等。然而,SRM转矩模型较复杂,制约了其推广应用。SRM建模方法主要包括线性法、准线性法和非线性法[5]。其中线性法和准线性法处理简单方便,但精度较低,而非线性法建模精度高,但以有限元磁链数据为基础,处理复杂,难以给出具体公式。
参考文献[6]针对直线SRM,借鉴参考文献[7-8]中12/8极电动机的椭圆磁路模型,通过磁路分割求解气隙磁导,再根据等效磁路模型,推导出直线SRM转矩模型。由于结构差异,12/8极椭圆磁路模型难以描述8/6极SRM的磁路分布特性,本文根据有限元仿真结果,建立了适用于8/6极SRM的新型椭圆磁路模型,求解了气隙磁路,进而推导出转矩数学模型,并验证了其正确性。
8/6极SRM单相励磁运行原理如图1所示。SRM转子在D相绕组通电的情况下,转动到D相定转子齿极正对位置,此时闭合磁通路径的磁阻最小;然后关断D相绕组电流,给A相绕组通电,Na为A相绕组匝数,ia为A相绕组电流,此时A相转子位移角θ=-15 °(定义定转子齿极正对时θ=0,顺时针方向为正);在电磁拉力作用下,SRM转子继续以顺时针转动,直到A相定转子齿完全正对,即θ=0时,关断A相绕组电流,使B相导通,继而实现A-B-C-D-A周期性导通,实现SRM旋转驱动。每相绕组在转子位移角θ=-15 °时导通,θ=0时关断,转动范围为(-15 °,0)。

图1 8/6极SRM单相励磁运行原理
本文以单相励磁8/6极SRM为研究对象,利用Maxwell 2D仿真软件建立二维模型,通过瞬态模块对其磁场做精确分析,SRM磁场分布结果如图2所示。A相绕组通电时,磁力线主要经由A相绕组定转子齿极构成电磁闭合回路,其他齿极处磁通量近似为0。以D相齿极处磁通量为例进行分析,原因如下:D相齿极处磁通量由匝数相等的Na1绕组回路和Na2绕组回路共同作用产生,由于电动机是中心对称结构,所以两回路气隙磁导相同;当忽略磁钢磁导时,两回路总磁导大小相等,即Na1绕组和Na2绕组可在D相齿极处产生大小相等、方向相反的磁通并相互抵消,使得D相齿极处磁通量近似为0,进而可忽略D相耦合。
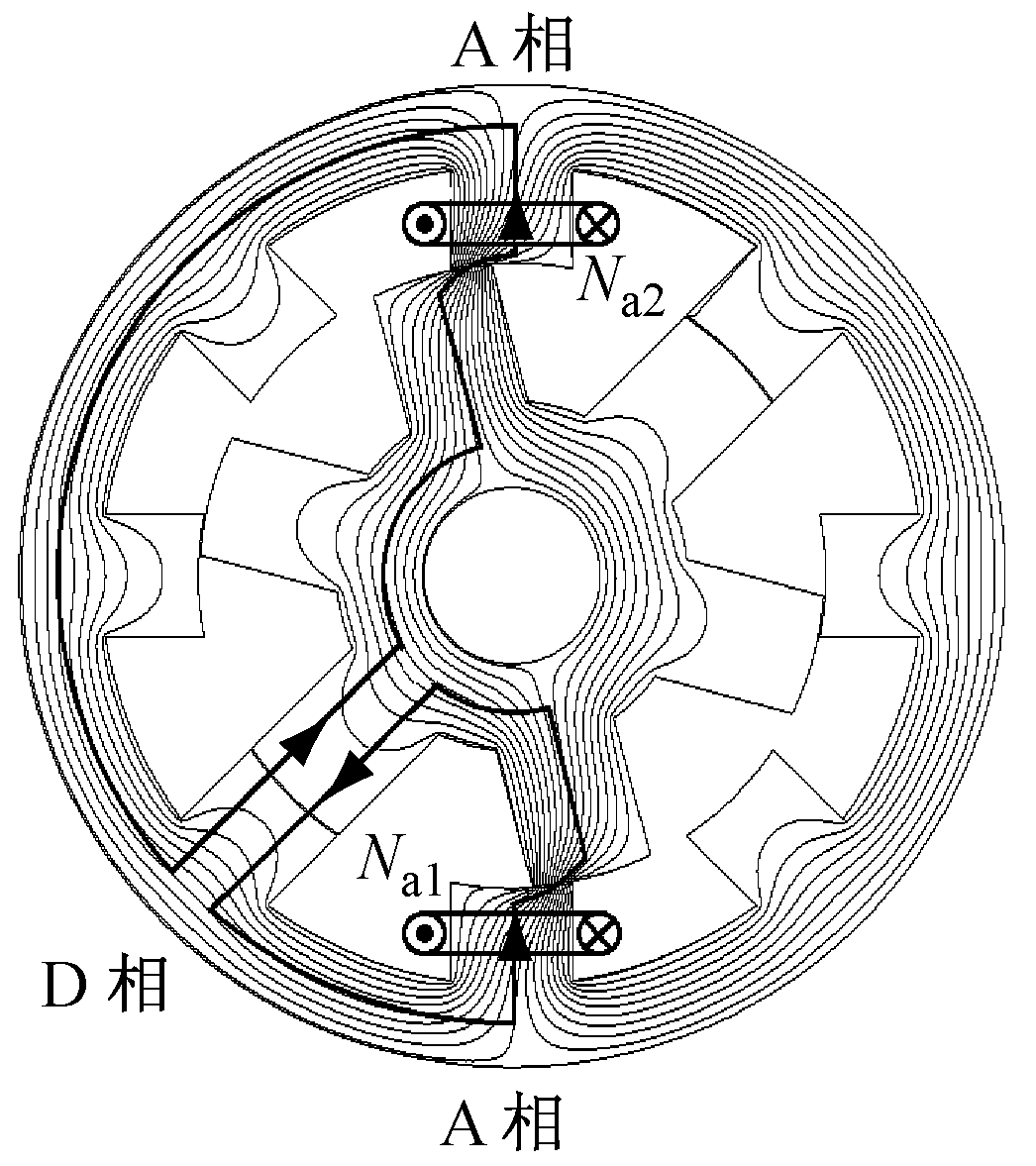
图2 SRM磁场分布
3.1 等效磁路模型
为简化分析,进行如下假设:① 忽略定转子磁通饱和与漏磁现象;② 忽略定转子磁钢磁导;③ 忽略与定子交链的转子轭部磁通。由图2可知,磁力线主要经由通电绕组定转子齿极形成回路,即分析等效磁路时,可仅考虑通电绕组定转子齿极处气隙磁导。以8/6极SRM的A相绕组为例,建立如图3所示的等效磁路模型。
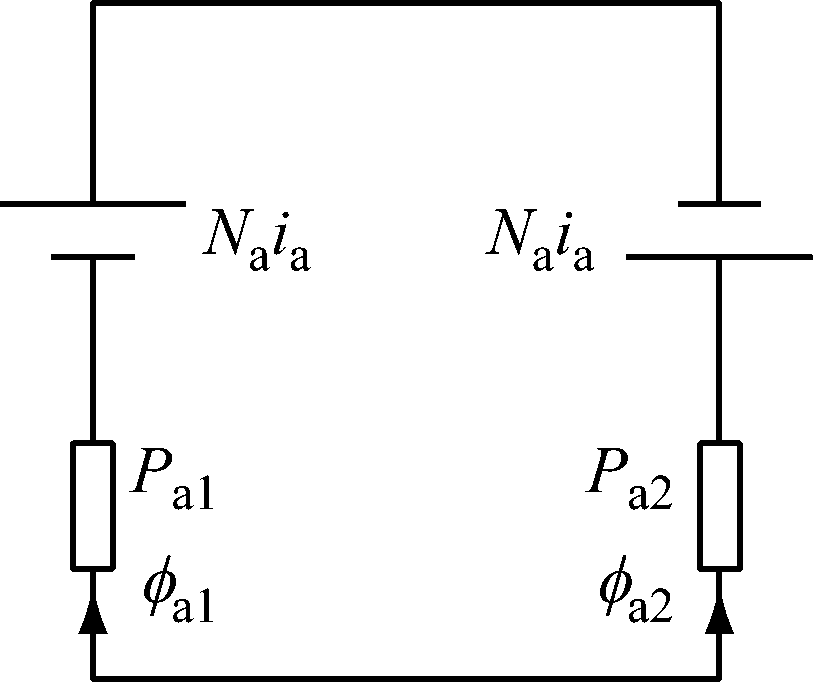
图3 A相绕组等效磁路模型
根据A相绕组等效磁路模型,得到磁路方程:

(1)
式中:φa1和φa2为A相2个齿极下的气隙磁通量;Pa1和Pa2为A相2个齿极下的气隙磁导。
根据式(1)得A相绕组自感系数为
(2)
3.2 新型椭圆磁路模型
借鉴参考文献[6]中横向磁场直线SRM气隙磁导求解方法,对8/6极SRM进行分割,如图4所示。其中P1为齿间磁导,即直线磁路部分磁导;P2和P3为边缘磁导,即椭圆磁路部分磁导;a为位于转子齿极弧面上的椭圆半轴长度;b为位于定子齿极侧面的椭圆半轴长度;r为转子半径。
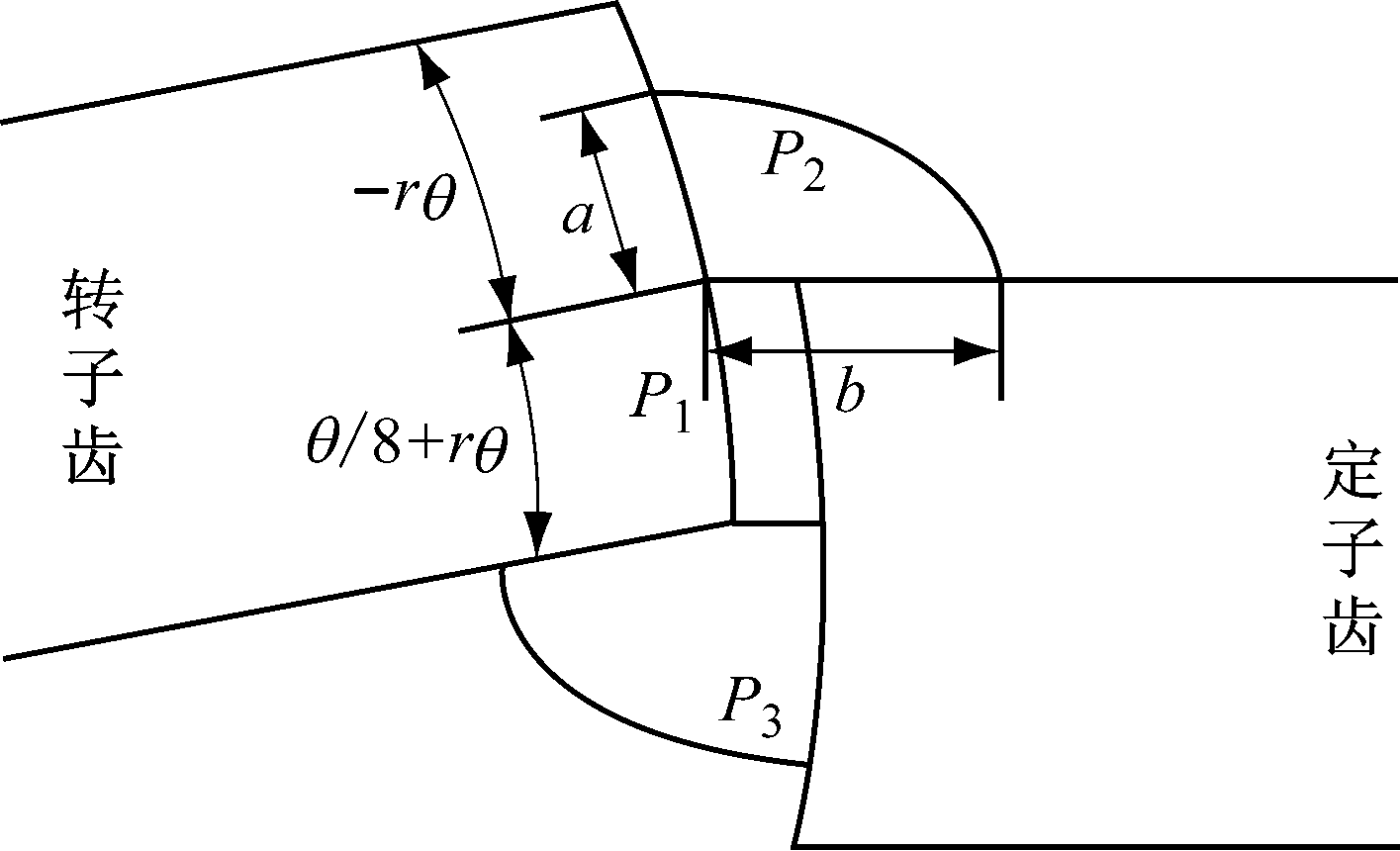
图4 磁路分割
横向磁场直线SRM在处理椭圆磁路分布特性时,采用了参考文献[7-8]中12/8极无轴承SRM的椭圆磁路模型公式。由于8/6极电动机齿极数与12/8极电动机齿极数不同,且定转子齿面弧度分别为22.5 °和15 °,所以,12/8极电动机的椭圆磁路模型不一定适用于8/6极电动机。现对8/6极SRM进行有限元仿真,获取定转子齿极间气隙处磁力线分布情况,如图5所示。

图5 气隙处磁路分布
由气隙处磁路分布可知,8/6极SRM气隙处的直线磁力线长度与气隙长度相等,即
(3)
式中:l为磁力线长度;lg为齿极间的气隙长度。
对于8/6极SRM的椭圆磁路部分(图5),当a趋近于0时,椭圆两半轴存在a<b关系,且随着a不断增大,会出现a>b的情况。参考文献[7-8]中8/12极电动机的椭圆磁路模型难以描述8/6极SRM气隙处的椭圆磁路线分布,因而需构建新的椭圆磁路模型。
根据有限元分析结果,建立如下新型椭圆磁路模型:
(4)
式中:x为描述a,b间关系的参数;m和n为椭圆模型系数。
用最小二乘法拟合曲线,解得新型椭圆模型系数:m=355 200,n=-292.3。
新型椭圆磁路模型与有限元仿真结果对比情况如图6所示,其中有限元仿真时选取转子位移角θ=-π/16。
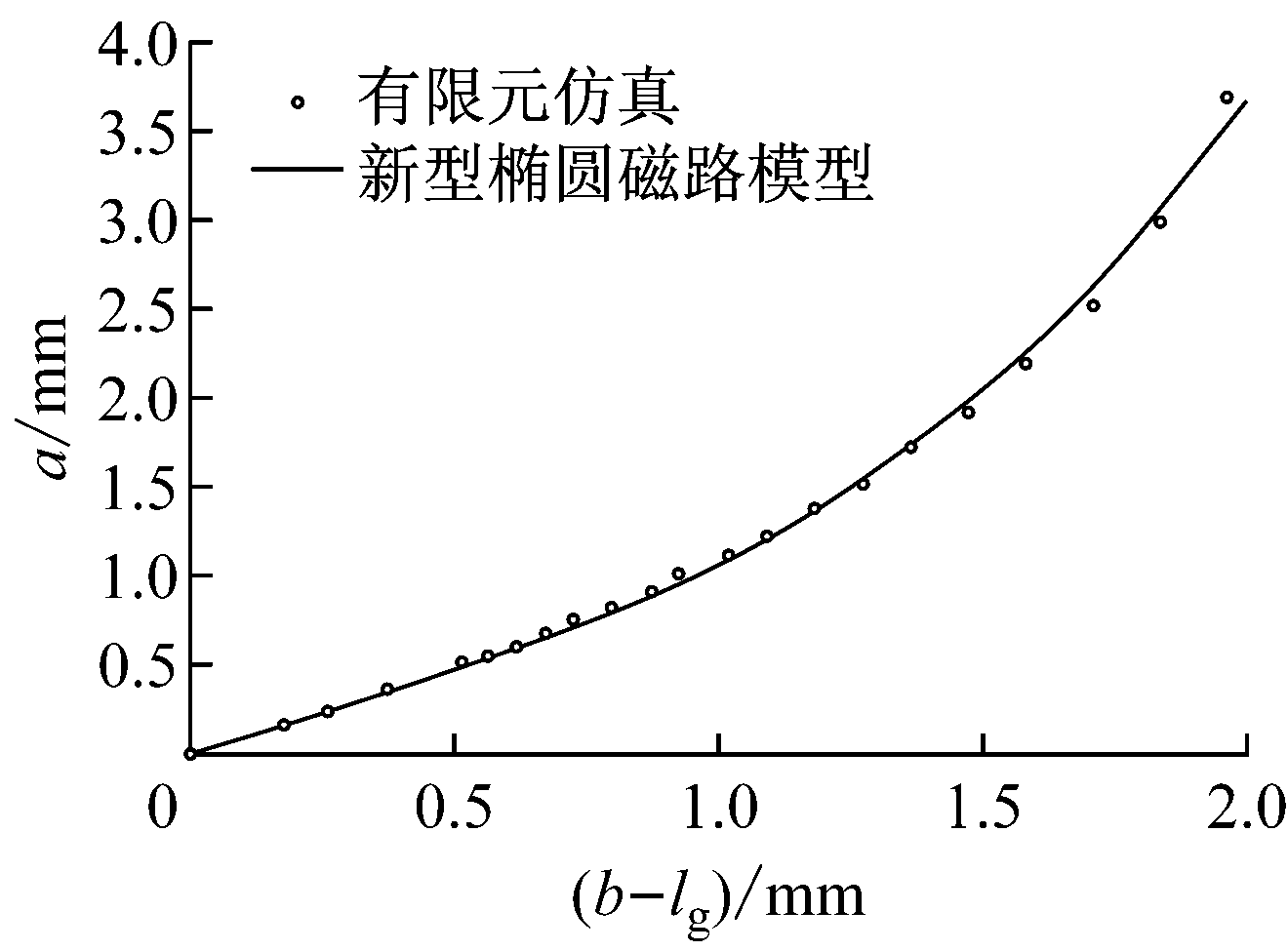
图6 新型椭圆磁路模型与有限元仿真结果对比
由图6可知,该新型椭圆磁路模型能较准确地描述8/6极SRM齿极气隙处磁力线的分布特性。由图4可知,新型椭圆磁路模型半轴最大长度a0与电动机转子位移角θ有如下关系:a0=-rθ。根据式(4),得
(5)
式中x0为椭圆半轴a=a0=-rθ时x的大小。
解式(5)可得
(6)
式中![]() ;
;![]() 。
。
3.3 气隙磁导
根据直线磁路模型可得齿间磁导P1为
(7)
式中:μ0为真空磁导;h为SRM轴向长度;θ∈[-π/8,0]。
椭圆磁路部分的边缘磁导P2求解过程:首先确定椭圆磁力线长度及微元面积,再结合微元磁导公式得出边缘磁导,具体过程如下。
针对新型椭圆磁路模型(式(4)),由于气隙长度为微小量,对x趋近于0时,a<b的情况不做考虑,即认为a为长半轴,b为短半轴。根据椭圆周长公式,得椭圆磁力线长度l=1/2πb+(a-b),联立式(4),得
(8)
已知磁导微元面积ds=1/2h(da+db),其中da为长半轴上的微元长度,db为短半轴上的微元长度。根据新型椭圆磁路模型(式(4)),可知
(9)
即有
(10)
已知微元磁导dP公式:
(11)
将式(8)和式(10)代入式(11),并积分得
(12)
由于8/6极SRM是中心对称结构,所以,气隙磁导Pa1=Pa2,联立式(7)、式(12),得
Pa1=![]()
![]() dx
dx
(13)
3.4 转矩数学模型
8/6极SRM的A相磁场储能Wa公式如下:
(14)
由虚位移理论可知,对SRM的磁场储能公式求关于转子位移角θ的偏导,可得转矩:
(15)
联立式(2)、式(13)和式(15),得
Ta=![]()
(16)
式中![]() 。
。
利用有限元软件仿真,得到θ∈(-22.5 °,0)时有限元输出转矩与转子位移角θ的关系,再利用Matlab绘制数学模型输出转矩关于转子位移角θ的曲线,通过比较验证转矩数学模型的正确性。
8/6极SRM模型1参数:定子铁芯外半径为30 mm,内半径为19.1 mm,定子轭环厚度为4.9 mm,定子齿极高为6 mm,定子齿极宽为7.45 mm;转子铁芯外半径为19 mm,内半径为5.36 mm,转子轭环厚度为5 mm,转子齿极高为8.64 mm,转子齿极宽为7.41 mm,电动机轴向长度为1 000 mm,每极绕组匝数为50。
8/6极SRM模型2参数:定子铁芯外半径为65.2 mm,内半径为37.2 mm,定子轭环厚度为13 mm,定子齿极高为15 mm,定子齿极宽为14.51 mm;转子铁芯外半径为37 mm,内半径为12 mm,转子轭环厚度为10 mm,转子齿极高为15 mm,转子齿极宽为14.44 mm,电动机轴向长度为1 000 mm,每极绕组匝数为100。
针对8/6极SRM模型1,设定SRM转子处于平衡位置,当绕组电流分别为3 A和3.5 A时,数学模型输出转矩和有限元输出转矩情况如图7所示。首先,随着转子位移角θ的增大,数学模型输出转矩越来越小,当θ=0°时,转矩等于0;其次,转矩对比结果表明,该数学模型输出转矩与有限元分析结果基本一致,即有较好的拟合效果。

图7 模型1数学模型输出转矩与有限元输出转矩对比
8/6极SRM转矩数学模型能描述模型1不同控制电流下的转矩输出,为验证转矩数学模型对其他尺寸的8/6极SRM是否具有通用性,特针对电动机模型2进行仿真,设定电动机模型2的转子处于平衡位置,结果如图8所示。由图8可知,当绕组电流分别为3 A和3.5 A时,Matlab转矩数学模型仿真曲线与有限元分析结果基本一致,即该转矩数学模型对于电动机模型2同样适用。

图8 模型2数学模型输出转矩与有限元输出转矩对比
通过Maxwell 2D有限元分析软件对单相励磁8/6极SRM气隙处磁路分布进行仿真,提出了一种新型椭圆磁路模型,用于描述气隙处的椭圆磁路分布特性。根据新型椭圆磁路模型,给出该模型下的气隙磁导求解方法,结合绕组自感公式和储能公式,推导出8/6极SRM的转矩数学模型,并通过有限元方法验证了该模型的正确性。
[1] 吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社,2000.
[2] 金鑫,簪小舒.双边开关磁阻直线电动机的设计[J].工矿自动化,2010,36(7):50-53.
[3] 张京军,龙荣,张海军,等.开关磁阻电机径向电磁力解析建模及有限元分析[J].煤炭学报,2012,37(4):700-704.
[4] 惠鸿忠,楚晓华.煤矿矸石山绞车用SRM调速系统的设计[J].工矿自动化,2010,36(1):98-101.
[5] 林委.计及互感的8/6极开关磁阻电机转矩估算模型研究[D].重庆:重庆大学,2014:5-7,41-50.
[6] 郭芳,葛宝明,张瑞芳.横向磁场直线开关磁阻电机的数学建模[J].电机与控制学报,2014,18(10):42-49.
[7] 邓智泉,杨钢,张媛,等.一种新型的无轴承开关磁阻电机数学模型[J].中国电机工程学报,2005,25(9):139-146.
[8] TAKEMOTO M, CHIBA A, AKAGI H, et al. Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation[C]//Conference Record of the Industry Applications Conference, Pittsburgh, 2002:35-42.
XIAO Linjing, LI Bo, SUN Chuanyu, WEN Yicheng, CHEN Zhongxia
(College of Mechanical and Electronic Engineering, Shandong University of
Science and Technology, Qingdao 266590, China)
Abstract:To study output torque characteristics of 8/6 switched reluctance motor, the principle of single-phase excitation of switched reluctance motor was expounded, and the magnetic field distribution in air gap between motor teeth was analyzed by finite-element analysis software Maxwell 2D. A new model of elliptic magnetic paths was established which can describe the elliptic magnetic paths of 8/6 switched reluctance motor. The air gap permeance was solved based on the model and the mathematic model of torque was derived when the motor stays balanced. Finally, the validity of mathematic model was certified by the results of finite-element analysis.
Key words:switched reluctance motor; single-phase excitation; mathematic mode; method of magnetic field division; finite-element analysis
作者简介:肖林京(1966-),男,山东沂水人,教授,博士,博士研究生导师,研究方向为机电液一体化和磁悬浮技术,E-mail:mr_libo@163.com。 刘成尧(1980-),男,安徽滁州人,讲师,硕士,研究方向为开关磁阻电动机两相励磁模式,E-mail:liulcy@163.com。
基金项目:山东省优秀中青年科学家科研奖励基金(BS2013NJ015);青岛市博士后研究人员应用研究项目(01020120521);青岛市应用基础研究计划项目(15-9-1-66-jch)。 2014年度高等学校国内访问学者专业发展项目(FX2014167)。
收稿日期:2015-11-26;修回日期:2016-02-25;责任编辑:胡娴。 2015-11-19;修回日期:2016-03-10;责任编辑:盛男。
中图分类号:TD614
文献标志码:A 网络出版时间:2016-04-05 11:33
文章编号:1671-251X(2016)04-0062-05
DOI:10.13272/j.issn.1671-251x.2016.04.015
肖林京,李波,孙传余,等.单相励磁8/6极开关磁阻电动机转矩数学模型[J].工矿自动化,2016,42(4):62-66.