煤层气水力压裂非线性滑模控制器设计

摘要：针对在煤层气开采过程中多个水力压裂水泵电动机的协调同步控制问题，提出了非线性滑模控制的方法，给出了水力压裂开采非线性滑模控制器的设计方法，并结合煤层气水力压裂系统对控制器性能进行了分析。仿真分析和实验结果表明，采用非线性滑模控制器后，在煤层气压裂开采中，煤层气的浓度和单孔流量均有较大程度提高。

0　引言

在煤层气开采中，水力压裂增透是一种较有效的煤层气增产技术[1]。煤层气水力压裂通常使用水泵对煤层进行注水压裂，在此过程中为了使煤层产生众多及延伸较远的裂缝，通常使用多个水泵进行注水。而由于各个电动机驱动的注水水泵所产生的压力不一致，往往使得水力压裂的总体效果不理想。为了保证煤层注水压裂效果，各个注水水泵在对煤层进行水力压裂时必须保持同步的压力变化[2]。这就对进行煤层气水力压裂的水泵电动机控制提出了较高的要求。

由于我国的煤层气注水压裂开采技术发展较晚，所以对用于煤层气注水开采的水泵电动机同步性研究较少。国外一些学者对电动机同步性进行了研究：Rodriguez-Angeles等[3]提出了“主-从”控制模式，选取其中一个电动机作为主机，而其他电动机作为从机，然后采用自抗扰和优化控制的算法进行同步控制；Franklin, Powell等[4-5]使用间接鲁棒串级控制，同时用改进PID方法对电动机同步性进行了研究；Khan, Spurgeon等[6]对电动机同步控制时的非线性和稳定性进行了研究；Sabanovic等[7]提出了自适应控制器, 同时对控制系统中出现的信号振颤进行了抑制，提高了电动机运行的同步性。这些控制算法基本对电动机模型的要求较高，在工程实际应用中受到了一定限制，在煤层气开发现场实施较为困难。

进行煤层气开采水力压裂的水泵电动机是三相异步电动机，一般认为三相异步电动机的动态模型是非线性、多变量的强耦合模型[8]。对于非线性对象的控制来讲，模型匹配很重要，而一旦模型不匹配则系统鲁棒性就会受到影响。在非线性控制方法中，滑模变结构控制可以克服系统模型的不确定性，对干扰和未建模动态具有较强的鲁棒性，对非线性系统的控制具有良好的效果[9]。

本文针对煤层气水力压裂开采过程中的电动机同步协调控制问题，结合非线性滑模变结构控制的基本原理，建立了注水泵三相异步电动机简化模型，提出了一种非线性滑模控制器设计方案。对该控制器进行了理论仿真，并应用于煤层气水力压裂开采过程，收到了较好的效果。

1　模型描述与控制器基本结构

在非线性控制方法中，滑模变结构控制对于模型的依赖性较低，因此，可以利用滑模变化结构控制将煤层气水力压裂系统的电动机模型进行简化。考虑到电动机的非线性特性，根据参考文献[8]中所提出的电动机模型进行如下简化：将电动机模型合并为线性一阶系统和几种非线性环节的共同作用。被控对象的模型结构如图1所示。

图1　被控对象的模型结构

图1中，被控对象的模型被简化为几个非线性环节。在外部信号施加于电动机系统时，输入时延和电压饱和是2个前置非线性模块；经过一阶线性的惯性环节后，系统输出转速信号，在电动机功率恒定的情况下，经过非线性运算(反比)得到输出转矩，而此输出转矩具有滞环非线性特性。由于在被控对象的线性部分存在非线性阻力，所以又构成非线性阻力的反馈环。

式中：E为系统偏差；X为驱动给定值，

，其中下脚标r表示给定参考值，P表示实际反馈值；M为系统回转部分的等效转动惯量，

；ΔT为电动机转矩误差，

；B为控制输入参数，其中包含系统的标称参数及未建模摄动范围，

。

由于系统要求同步性较高，所以还需加入系统给定参考Er与实际反馈值EP的误差：

在水力压裂开采煤层气时，要对各个注水水泵电动机进行控制，使其压力变化保持同步，才能收到满意的效果。根据系统的控制要求并结合电动机模型，考虑到系统本身的非线性环节较多，存在模型不匹配的问题，对系统的鲁棒性将会有较大影响，本文提出使用滑模变结构控制策略进行控制，将系统控制过程分为2步，而这2步具有不同的控制结构：首先，使系统状态在有限的时间内达到一定的滑动流形；然后，在未来时间内将系统状态轨线保持在该流形上。由于滑模运动与系统状态的不确定性无关，所以可以很好地保持系统的鲁棒性[10]。

煤层气水力压裂系统由多个注水泵构成，在控制过程中以其中一台作为系统的给定参考输入(可看作主机)，使其他设备(可看作从机)的同步误差与系统给定参考输入最小。系统非线性滑模控制器基本结构(一主多从结构)如图2所示。

图2　系统非线性滑模控制器基本结构

水力压裂系统的标称模型由图1给出，同步误差向量E、外部扰动及未建模动态由观测器1进行估计，其动态变化特性由观测器2 估计。整个控制器集中于2个观测器的设计，配合系统标称模型进行控制，使整个系统的同步误差满足煤层气水力压裂开采的具体要求，同时使系统具有较好的鲁棒性。

2　非线性滑模控制器设计与分析

式中：ρ为观测器的增益矩阵；Γ为变换矩阵；H+为矩阵H的伪逆阵；K为观测扰动的预设界；λ为滑模面参数。

根据控制指标设计系统滑模控制器，首先选定稳定滑模面，定义滑模面S为

式中：λ=diag(λr,λP,λε)，此参数阵对滑模面上的误差收敛速度进行限定，可消除滑模面上的开环动态偏差。

对于外界扰动估计值

，可对式(7)所决定的滑模面进行积分获得：

滑模面S的前2个分量体现了系统的同步动态性，为提高系统刚度和强鲁棒性提供了条件。根据式(7)、式(8)并结合收敛的抗饱和条件[12]，可得滑模面切换条件：

当系统外扰超过预设边界条件，而且误差状态未位于收敛轨线的滑动流形上时，观测器要将饱和限控制在

-]内，以确保系统鲁棒性。

式中：

为饱和限真实值d与估计值

之间的动态偏差，

；权矩阵N为系统惯量加权逆。

式(11)所示的Lyapunov函数为正定。根据系统稳定性条件，若系统稳定，必须要

<0成立。忽略计算过程中对系统性能无影响的系数问题，则有

首先，讨论系统稳定性，将系统控制律式(15)代入Lyapunov函数式(11)，则系统强迫运动为

此时，滑动流形S、系统偏差及其微分以及外界

式(10)之内。考虑到系统数学模型的动态性，有

由于

有界，故滑模面微分

亦有界。参考文献[14]已证明：当t→∞时，系统滑模面及误差均可收敛于系统原点。由此可知，本系统的控制律为全局渐进稳定。

可见，该控制律非常类似于带有前馈补偿的PID控制律。在忽略控制律前馈项的情况下，可将此控制器看作多输入多输出PID控制器，其控制参数矩阵为

式中：

分别为第1渐近控制律的比例、积分、微分系数；CrP=ΚprP+ΚDrPs, KPrP，KDrP分别为第2渐近控制律的比例、微分系数；CPr=ΚpPr+ΚDPrs,KpPr，KDPr分别为第3渐近控制律的比例、微分系数；

分别为第4渐近控制律的比例、积分、微分系数。

若系统的动态性有界，则式(19)为准对称矩阵。根据系统动态模型(式(3))，经变换后，可得系统动态误差表达式：

从式(20)可以看出，同步误差ε已由失配扰动dr-dP所限定，在控制过程中，失配扰动一旦为零，则系统的同步偏差也将为零。

3　仿真与实验分析

首先，将多电动机系统简化为双电动机系统，使其中之一作为主机，另一台作为从机，从机与主机保证同步性，即一主一从结构；然后陆续添加其他电动机，与主机保持同步性；最后调节各从机之间的同步误差，渐次达到一主多从的同步要求。

各注水泵系统的等效标称参数(以一主一从结构为例)见表1，表中参数为实际参数向控制量端的电压折合值。

表1　一主一从结构注水泵系统标称参数

系统此时为多输入多输出系统，设其传递函数矩阵为L(jω)，定义灵敏度函数为[7]

根据系统稳定性的要求及系统的控制律，可得系统的控制参数，见表2。

表2　系统控制参数

在此基础上进行同步精度的仿真分析。主、从机水力载荷(输出压力)的动态变化及其偏差如图3所示。由于在煤层气水力压裂系统中突变信号较少[1]，所以在仿真过程中采用正弦信号作为激励信号，以考核系统中多个电动机的载荷(输出压力)变化的同步性[15]。由图3(a)可以看出，主、从机的同步性保持较好。控制过程中主、从机的水力载荷(输出压力)偏差变化趋势如图3(b)所示，其偏差信号近似白噪声，偏差的方差保持在1～2 MPa，且随着时间的不断推移，系统偏差的方差有进一步减少的趋势，最终稳态方差维持在1 MPa以内。

在山西省某矿井高瓦斯(煤层气)煤层进行实验[16]，水力压裂抽采钻场选定在该煤层的低瓦斯(煤层气)区，以考核系统的实施效果。以矿用便携式PC机作为上位控制计算机，采用ACS800系列标准变频器进行控制，多传动模块选用 ACS800-04-0075-3+P901，水力压裂泵选用DM46-50×5型卧式多级矿用注水泵。实验过程中采用一主两从的控制模式。煤层气水力压裂开采现场布置如图4所示。

(a) 主、从机水力载荷动态变化

(b) 主、从机水力载荷偏差

图3　主、从机水力载荷(输出压力)动态变化及偏差

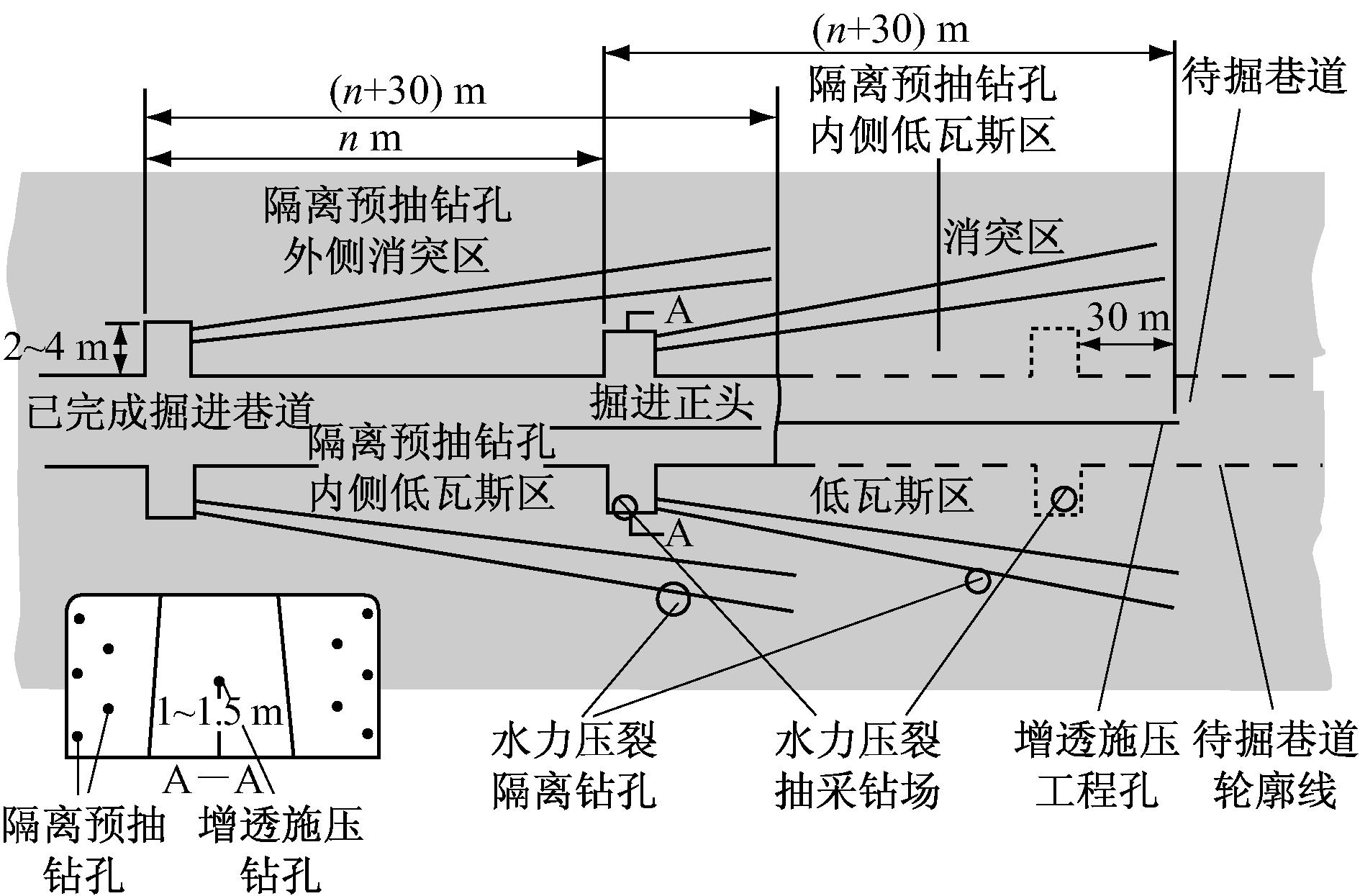
图4　煤层气水力压裂开采现场布置

实验时，首先对未采用本文方案的水力压裂开采进行约一昼夜的观测，随即暂时封堵注水孔[17]。待预裂基本稳定后，按照本文所述再进行压裂实验，也进行约一昼夜观测。2种方案煤层气的涌出情况对照如图5所示。从图5可以看出，采用本文方案后，该煤层的煤层气涌出情况有很大的改善。在煤层气流量方面，前10 h的情况改善一般。但在其后的时间里，流量明显增大，且维持稳定，涌出的煤层气浓度也有较大幅度提高。

(a) 煤层气体积分数变化

(b) 煤层气流量变化

图5　2种方案煤层气的涌出情况

4　结语

针对煤层气开采过程中水力压裂的总体效果不理想的问题，设计了非线性滑模控制器，对采用非线性滑模控制器的水力压裂系统进行了仿真和实验，结果表明：① 水力压裂系统对数学模型的依赖性较小，具有较强的鲁棒性。② 水力压裂系统可在较短时间内实现多台注水水泵电动机的同步运行，系统水力载荷(输出压力)的同步误差较小，相对误差不大于3%。经实验证明，在煤层气压裂开采中，煤层气的体积分数和单孔流量均有较大程度提高。③ 文中的滑模控制律类似于带有前馈补偿的PID控制律，在工程实践中便于实现，具有较强的可操作性，在相似的煤层地质条件下便于进行实验性推广。

[1]　万玉金,张劲,王新海,等．煤层气经济开采增产机理研究[M]．北京：科学出版社，2011：18-19．

[2]　赵庆波,李贵中,孙粉锦,等.煤层气地质选区评价理论与勘探技术[M].北京:石油工业出版社,2009: 1-4.

[3]　RODRIGUEZ-ANGELES A, NIJMEIJER H. Synchronizing tracking control for flexible joint robots via estimated state feedback[J]. Journal of Dynamic Systems,Measurement and Control,2004,126(1)：162-172.

[4]　FRANKLIN F,POWELL J D,EMAMI-NAEINI A. Feedback control systems[M]. 6th edition. New Jersey: Prentice Hall, 2009: 89-95.

[5]　姚舜才,潘宏侠.粒子群优化同步电机分数阶鲁棒励磁控制器[J].中国电机工程学报,2010,30(21):91-97.

[6]　KHAN M K, SPURGEON S K, LEVANT A. Simple output feedback 2-sliding controller for systems of relative degree two[C]//Proceedings of the European Control Conference, Cambridge, 2003.

[7]　SABANOVIC A. Variable structure systems with sliding modes in motion control-a survey[J]. IEEE Transactions on Industrial Informatics, 2011, 7(2):212-223.

[8]　阮毅,陈伯时.电力拖动自动控制系统——运动控制系统[M].4版.北京：机械工业出版社,2010：218-220．

[9]　李殿璞.非线性控制系统[M].西安：西北工业大学出版社,2009：392-396．

[10]　方勇纯,卢桂章.非线性系统理论[M].北京:清华大学出版社,2009:86-91.

[11]　MUSKE K R, ASHRAFIUON H, NERSESOV S, et al. Optimal sliding mode cascade control for stabilization of under actuated non-linear systems[J]. Journal of Dynamics Systems, Measurement and Control, 2012, 134(2):1-11.

[12]　MIHOUB M, NOURI A S, ABDENNOUR R B．A second order discrete sliding mode observer for the variable structure control of a semi-batch reactor[J]．Control Engineering Practice,2011,19(10):1216-1222．

[13]　SENCER B, MORI T, SHAMOTO E. Design and application of a sliding mode controller for accurate motion synchronization of dual servo systems[J]. Control Engineering Practice, 2013,21(8):1519-1530．

[14]　SLOTINE J J E, LI W. Adaptive manipulator control: a case study[J]. IEEE Transactions on Automatic Control, 1988, 33(11):995-1003.

[15]　VOLPONI A J, DEPOLD H, GANGULI R, et al.The use of Kalman filter and neural network methodologies in gas turbine performance diagnostics: a comparative study[J]. Journal of Engineering for Gas Turbines and Power, 2003, 125(4):917-924.

[16]　傅雪海, 秦勇,李贵中,等. 山西沁水盆地中、南部煤储层渗透率影响因素[J].地质力学学报,2001,7(1):45-52.

[17]　覃建华,肖晓春,潘一山,等.滑脱效应影响的低渗储层煤层气运移解析分析[J].煤炭学报,2010,35(4):619-622.

Design of nonlinear sliding mode controller for hydraulic fracturing of coalbed methane

(1.School of Computer Science and Control Engineering, North University of China,Taiyuan 030051, China; 2.School of Resource and Safety Engineering,China University of Mine and Technology(Beijing), Beijing 100083, China)

Abstract：For coordination and synchronous control problem of multi motors of water pump for hydraulic fracturing in coalbed methane exploit process, a method of nonlinear sliding mode control was proposed, design method of nonlinear sliding mode controller for hydraulic fracturing of coalbed methane was given, and the controller performance was analyzed combining with hydraulic fracturing system of coalbed methane. The simulation analysis and experimental results show that concentration and single hole flow rate of coalbed methane were increased greatly in the process of coalbed methane fracturing exploit.

Key words:coalbed methane exploit; hydraulic fracturing; nonlinear sliding mode control

作者简介：姚舜才(1973-)，男，山西阳泉人，副教授，博士，研究方向为煤层气新型开采方法、非线性系统辨识与建模、电机控制系统，E-mail: yaoshuncai@nuc.edu.cn。

基金项目：山西省煤层气联合研究基金资助项目(2013012010)；山西省新兴产业领军人才(创新)项目(2014-052)。

收稿日期：2015-11-25；修回日期：2016-01-05；责任编辑：胡娴。

网络出版地址：http://www.cnki.net/kcms/detail/32.1627.TP.20160307.1522.016.html

姚舜才，马铁华，李峰.煤层气水力压裂非线性滑模控制器设计[J].工矿自动化，2016,42(3)：69-74.

煤层气水力压裂非线性滑模控制器设计

0 引言

1 模型描述与控制器基本结构

2 非线性滑模控制器设计与分析