张伟强1,2， 王恩元1,2， 李学龙1,2， 孔祥国1,2， 李国爱1,2
(1.中国矿业大学 安全工程学院， 江苏 徐州 221116;
2.煤矿瓦斯与火灾防治教育部重点实验室， 江苏 徐州 221116)
摘要：针对目前煤岩冲击倾向性评价方法存在的不足，基于海明距离法基本原理，建立了煤岩冲击倾向性综合评价模型。该模型选用动态破坏时间、冲击能量指数、弹性能量指数和煤岩单轴抗压强度作为综合评价指标，应用线性内插公式构造评价对象的隶属函数，采用海明距离法获得评价对象与评价标准的相似程度，并用最小海明距离进行类别评判，从而得出评价结果。实例分析结果表明，海明距离法的评价结果与煤样的实际现场冲击倾向性一致；对处于同一冲击倾向性级别的煤样的海明距离大小进行对比，结果认为海明距离法比模糊综合评判法和熵权-理想点法具有更高的分辨率。
关键词：煤岩冲击倾向性； 海明距离； 线性内插； 次贴进度
煤岩动力灾害-冲击地压以其突然、剧烈、猛烈的破坏特征对煤矿、金属矿井、隧道等的安全构成严重威胁，甚至造成巨大的经济损失和人员伤亡。随着矿井开采深度的增加，冲击地压的危险也在逐步增加，已成为制约矿井安全生产的重大隐患。国内外学者研究表明，煤岩具有冲击倾向性是发生冲击地压的必要条件[1]。对煤岩冲击倾向性进行合理有效的评价，是防治冲击地压的理论及实践基础。
目前煤岩冲击倾向性评价指标主要有动态破坏时间、弹性能量指数、冲击能量指数和单轴抗压强度[2]。在煤岩冲击倾向性的综合评价过程中，这4个指标值往往同时处于不同的冲击倾向性级别中，难以准确判断采用哪个指标[1]。针对煤岩冲击倾向性的研究中，齐庆新等[3]指出单轴抗压强度可以与动态破坏时间、弹性能量指数、冲击能量指数一样作为煤岩冲击倾向性的评价指标；赵同彬等[4]进行了基于颗粒流理论的煤岩冲击倾向性细观模拟试验研究，但仅研究了单轴抗压强度和弹性能量指数对煤岩倾向性的影响；潘一山等[5]进行了煤层冲击倾向性与危险性评价指标研究，提出了临界应力系数、临界软化区域系数、冲击能量速度这3项新的评价指标，但无法准确计算出巷道发生冲击地压时的临界岩体应力和临界尺寸；白汉营等[6]应用模糊综合评判法评价煤岩冲击倾向性，在运算过程中舍去了一部分影响因素，导致隶属函数值被权重系数值代替；王超等[7-8]采用熵权-理想点法综合评价煤岩冲击倾向性，该方法无法区分处于同一冲击倾向性的多种煤样间的冲击倾向性强度。
海明距离法是一种多目标、多因素的综合评价方法[9-11]，其原理简单、科学，操作性强，能够将多因素、多对象的模糊问题定量化，从而更准确、更科学地评价模糊事件。海明距离法已应用于空气质量评价[12]、垃圾填埋场地下水质量评价[13]、矿井通风系统评价[14]等领域，但在煤岩冲击倾向性评价方面的应用还缺乏系统研究。本文采用海明距离法对煤岩冲击倾向性进行综合评价，采用线性插值法构造评价对象的隶属函数，来避免权重系数值代替隶属函数值的问题，并采用更加客观、科学的双指标表示评价结果。
海明距离法通过选取最小海明距离来评判煤岩冲击倾向性级别。其原理：首先选取各评价标准模糊集下确界构成评价标准矩阵，再将该矩阵转换为评价标准隶属度矩阵，然后针对评价矩阵，运用线性内插公式构造评价对象隶属度矩阵，最后求取各评价对象隶属度矩阵与评价标准隶属度矩阵间的海明距离，并将海明距离按大小进行排序，选取最小的海明距离。
1.1 确定评价因子和评价标准
假设有n个评价对象，每个评价对象有m个评价因子，则有n×m阶评价矩阵：
(1)
式中：aij为第i(i=1,2，…，n)个评价对象的第j(j=1,2，…，m)个评价因子。
假设有t级评价标准，则对于n个评价对象，有t×m阶评价标准矩阵：
(2)
引入线性内插公式，得aij的隶属值：
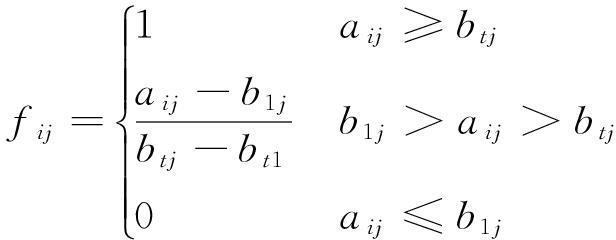
(3)
式中：b1j,btj分别为第j个评价因子的1,t级评价标准值。
用式(3)将式(1)转换为评价对象隶属度矩阵：
(4)
煤的冲击倾向性评价具有模糊性。考虑2种极端情形，即无冲击倾向性煤样和强冲击倾向性煤样，其余任何一种煤样均介于这2种极端情形之间。所有的煤样因各自不同的特点，对无冲击倾向性煤样和强冲击倾向性煤样分别具有不同的隶属度。假设无冲击倾向性煤样和强冲击倾向性煤样的m个评价因子分别对自身的隶属度为0和1，得到某煤样对自身的隶属度：
(5)
式中：bhj为第j个评价因子的h(h=1,2,…,t)级评价标准值；chj为bhj的隶属度。
利用式(5)将式(2)转换为评价标准隶属度矩阵：
(6)
1.2 评价原则与评价方法
海明距离法在求评价对象与标准对象的相似程度上可有效提高评价结果的分辨率。假设评价对象d和标准对象e均包括m个评价因子x1,x2,…,xm，且评价对象d对xj的隶属度为μd(xj)，标准对象e对xj的隶属度为μe(xj)，则评价对象d与标准对象e之间的海明距离为
(7)
μd(xj)为式(3)中的fij；μe(xj)为式(5)中的chj。
加权海明距离为
(8)
式中wj为第j个评价因子的权重。
(9)
由此可得评价对象隶属度矩阵与评价标准隶属度矩阵之间的加权海明距离：
(10)
由式(10)求出的海明距离为
内的具体值。海明距离越小，说明煤样冲击倾向性与评价标准之间的差别越小，反之越大。
2.1 评价因子与评价标准的选取
根据参考文献[2]，选取动态破坏时间(DT)、弹性能量指数(WET)、冲击能量指数(KE)和单轴抗压强度(RC)作为煤岩冲击倾向性评价因子，根据评价结果将煤岩冲击倾向性分为无冲击倾向性(Ⅰ)、弱冲击倾向性(Ⅱ)、强冲击倾向性(Ⅲ)3类。各评价标准单因子模糊分级界限见表1。
表1 煤岩冲击倾向性各评价标准单因子模糊分级界限
2.2 评价结果
选取实测煤样数据[8]进行煤岩冲击倾向性等级判定，实测数据见表2。
表2 某煤矿煤岩冲击倾向性实测数据
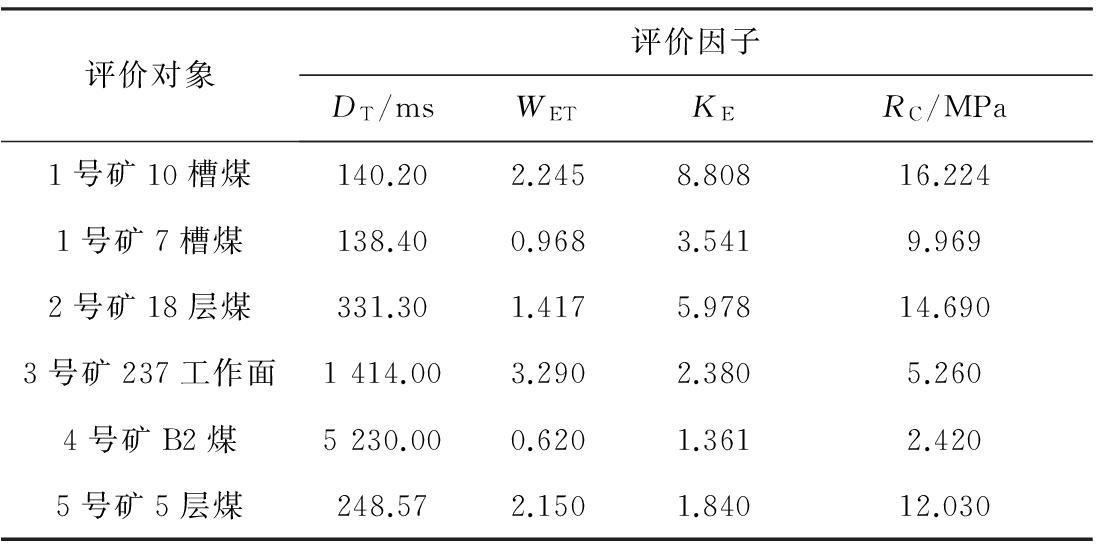
由表2可得6个评价对象的4个评价因子实测数椐构成的矩阵：
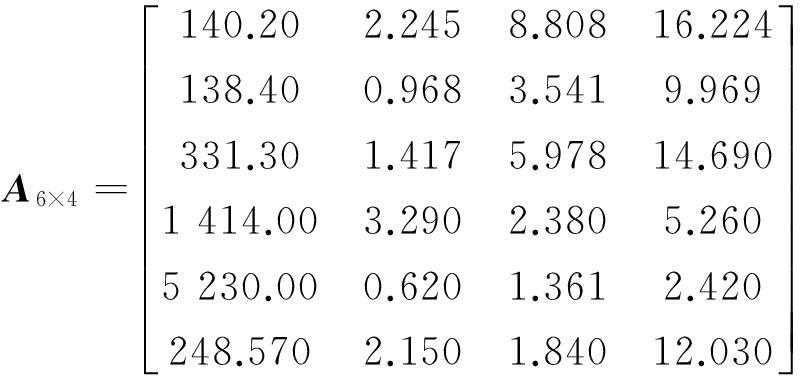
(11)
根据模糊集距离的概念进行模糊评价，均需确定单因子各级模糊界限值。其一般由式(12)确定：
(12)
式中
为第j个评价因子h级评价标准最小值。
由式(12)处理表1数据可得3×4阶煤岩冲击倾向性评价标准矩阵：
(13)
假设无冲击倾向性煤样和强冲击倾向性煤样的m个评价因子分别对应自身的隶属度为0和1，由式(5)可将评价标准矩阵B3×4转换为评价标准隶属度矩阵：
(14)
由式(3)可将实测数据矩阵A6×4转换为评价对象隶属度矩阵：
(15)
由式(9)得到6个评价对象、4个评价因子的权重矩阵：
(16)
经归一化可得
(17)
由式(10)可计算出各评价对象的海明距离，见表3。
表3 各评价对象的海明距离
从表3可看出，6个评价对象的最小海明距离分别为0.139，0.361，0.158，0.184，0.009，0.258。可知1号矿10槽煤、1号矿7槽煤、2号矿18层煤、3号矿237工作面、4号矿B2煤和5号矿5层煤这6种煤样的冲击倾向性分别与强冲击倾向性级别、弱冲击倾向性级别、强冲击倾向性级别、无冲击倾向性级别、无冲击倾向性级别和弱冲击倾向性级别最贴近，即认为6种煤样的冲击倾向性分别属于强冲击倾向性、弱冲击倾向性、强冲击倾向性、无冲击倾向性、无冲击倾向性、弱冲击倾向性。
2.3 评价结果分析
煤样的实际现场冲击倾向性与模糊综合评判法[7]、熵权-理想点法[8-9]、海明距离法的评价结果见表4。
表4 不同方法评价结果对比
由表4可知，海明距离法的评判结果与煤样的实际现场冲击倾向性一致，说明海明距离法可作为一种评价煤岩冲击倾向性的有效方法。根据煤样的实际现场冲击倾向性知，3号矿237工作面与4号矿B2煤的冲击倾向性处于无冲击倾向性类别，则海明距离法的评价结果与熵权-理想点法评价结果相比具有更高的准确性。
2.4 次贴进度比较
在对所有的煤样进行分级之后，为了能在评价结果中体现出处于同一级别的各煤样冲击倾向性差别，引入次贴进度[11]概念，即求取处于同一级别各评价因子与相邻2个评价标准间的海明距离
，用
表示处于同一级别各评价因子之间的差别。本文仅对上一级评价标准求取次贴进度，并将其表示为双指标形式，如煤岩冲击倾向性被评为(III/II)，则可得出该煤样的冲击倾向性被划为具有强冲击倾向性(III)煤，但对具有弱冲击倾向性(II)煤的次贴进度为，且
。
由表3知，1号矿7槽煤的冲击倾向性和5号矿5层煤的冲击倾向性都处于弱冲击倾向性(II)，但二者对无冲击倾向性(I)的次贴进度分别为0.582和0.591。因此，1号矿7槽煤的冲击倾向性要弱于5号矿5层煤的冲击倾向性，且该结果与煤矿实际现场情况相符合。由此得到6种煤样的双指标评价结果：
(II/I):1号矿7槽煤(0.582)的冲击倾向性要弱于5号矿5层煤(0.591)的冲击倾向性。
(III/II):1号矿10槽煤(0.552)的冲击倾向性要强于2号矿18层煤(0.476)的冲击倾向性。
从双指标评价结果可知海明距离以量化概念表征煤岩冲击倾向性的进展程度，直观地描述煤岩冲击倾向性的分布规律，有利于掌握煤岩冲击倾向性的具体情况。另外，海明距离法评价结果与模糊综合评判法、熵权-理想点法评价结果相比具有更高的分辨率。
将海明距离法引入煤岩冲击倾向性评价中，并提出一种用线性插值构造各评价对象隶属函数的新方法，采用双指标表示评价结果，建立了基于海明距离法的煤岩冲击倾向性综合评价模型，得出以下结论：
(1) 海明距离法评价结果与煤矿现场冲击倾向性一致，证明海明距离法可以作为一种新的、有效的煤岩冲击倾向性评价方法。
(2) 在区分处于同一冲击倾向性级别的煤岩冲击倾向性强弱方面，海明距离法与模糊综合评判法、熵权-理想点法相比具有更高的分辨率。
(3) 与模糊综合评判法相比，海明距离法应用线性内插公式构造评价对象的隶属函数，避免权重系数值代替隶属函数值的现象，同时具有计算过程简洁、可操作性强的优点；与熵权-理想点法相比，海明距离法评判结果具有更高的准确性和科学性。
参考文献：
[1] 窦林名,何学秋.冲击矿压防止理论与技术[M].徐州：中国矿业大学出版社，2001.
[2] GB/T 25217.2—2010冲击地压测定、监测与防治方法 第2部分：煤的冲击倾向性分类及指数的测定方法[S].
[3] 齐庆新,彭永伟,李宏艳,等.煤岩冲击倾向性研究[J].岩石力学与工程学报,2011,30(1):2736-2742.
[4] 赵同彬,尹延春,谭云亮,等.基于颗粒流理论的煤岩冲击倾向性细观模拟试验研究[J].煤炭学报,2014,39(2):280-285.
[5] 潘一山,耿琳,李忠华.煤层冲击倾向性与危险性评价指标研究[J].煤炭学报,2010,35(12):1975-1978.
[6] 白汉营,王档良，李文平.模糊综合判别法在煤层冲击倾向性评价中应用[J].能源技术与管理,2006(1):21-22.
[7] 王超,王恩元,刘晓飞.基于熵权-理想点法的煤层冲击倾向性分类[J].辽宁工程技术大学学报:自然科学版,2012,31(6):838-842.
[8] 王迎超,尚岳全,孙红月,等.基于熵权-理想点法的岩爆烈度预测模型及其应用[J].煤炭学报,2010,35(2):218-221.
[9] 李鸿吉.模糊数学基础及实用算法[M].北京:科学出版社,2005：282-284.
[10] 陈鸣剑,张志烈,樊宝康.模糊数学及其实用[M].南京：河海大学出版社,1993：94-95.
[11] 陈启浩.模糊值及其在模糊推理中的应用[M].北京:北京师范大学出版社,2000：97-171.
[12] 高淑环,李晓奇.海明模糊距离法在空气质量评价中的应用[C]//第11届中国不确定系统年会、第15届中国青年信息与管理学者大会论文集,2013:43-46.
[13] 安达,姜永海,杨昱,等.海明距离模糊法在垃圾填埋场地下水质量评价中的应用[J].环境工程技术学报,2013,3(2):119-123.
[14] 谢贤平,赵梓成.应用海明距离公式评价矿井通风系统[J].四川冶金，1996(1):6-10.
ZHANG Weiqiang1,2, WANG Enyuan1,2, LI Xuelong1,2, KONG Xiangguo1,2, LI Guoai1,2
(1.School of Safety Engineering, China University of Mining and Technology, Xuzhou 221116, China;
2.Key Laboratory of Mine Gas and Fire Disaster Prevention and Control of Ministry of Education,
Xuzhou 221116, China)
Abstract:In allusion to shortcomings of current evaluation methods about rock burst tendency of coal seam, a model was built for comprehensively evaluating rock burst tendency of coal seam on basis of Hamming distance theory. Dynamic failure time, impact energy index, elastic energy index and uniaxial compressive strength are selected as comprehensive evaluation indexes in the model. Membership functions of evaluation objects are structured by use of linear interpolation formula. Then similar degree between the evaluation objects and standard objects is gotten respectively by Hamming distance method. Evaluation results are gotten through using the minimum Hamming distance to evaluate classification. The analysis result of actual example shows that the evaluation results of Hamming distance method are consistent with rock burst tendency of coal seam in actually field; by contrasting Hamming distances of coal samples which are at the same burst tendency level, it is found that Hamming distance method has a higher resolution ratio than fuzzy comprehensive evaluation method and entropy-ideal point method.
Key words:rock burst tendency of coal seam; Hamming distance; linear interpolation; secondary close degree
中图分类号：TD713.2
文献标志码：A 网络出版时间：2016-01-26 15:39
文章编号：1671-251X(2016)02-0007-05
DOI:10.13272/j.issn.1671-251x.2016.02.002
张伟强，王恩元，李学龙,等.基于海明距离法的煤岩冲击倾向性评价[J].工矿自动化，2016,42(2)：7-11.