图1 直流微网结构
张勇， 徐瑞东， 李涛， 徐善玉, 王龙
(中国矿业大学 信息与电气工程学院， 江苏 徐州 221116)
摘要：研究了基于多级功率变换器下的直流微网结构，提出恒功率负载研究方法，建立了直流微网简化模型；根据简化模型，建立了DC-DC双向变换器在不连续运行模式下的离散映射，给出了系统稳定运行状态下迭代方程和反馈系数的计算公式；根据迭代方程得出电压与反馈系数的分岔波形图。电路仿真和实验结果表明，随着反馈系数的增大，系统将从稳定状态到分岔状态并逐渐过渡到混沌状态。
关键词：直流微网； 双向变换器； 恒功率负载； 离散映射； 分岔
在配电系统中，直流微网对于满足电能质量要求以及可再生能源的集中利用具有重要作用[1]。事实上，由于可再生能源的集中利用以及系统中直流电子负载的增多，使得人们越来越多地关注和研究直流配电方式，从而建立了更为高效的供电系统。直流微网运行灵活，既可以和主电网连接起来并网运行，也可以运行在孤岛模式下。此外，由于直流微网系统中应用新一代功率变换器，使得直流分布式发电比交流分布式发电具有更高的效率[2]。因此，直流微网发展十分迅速。
直流微网是利用多级功率变换器把多种负载和发电源连接起来的结构[3]。直流微网的级联拓扑结构以及对DC-DC变换器的严格控制，使得变换器的输入端呈现出恒功率负阻抗特性，而一般的线性控制技术不适合控制这种非线性负载，变换器的使用可能导致输出电压和电流出现分岔现象[4-5]。参考文献[6]中对Buck闭环电路进行了仿真，通过改变输入电压和电容参数得到不同的分岔和混沌相图。参考文献[7]中对Buck闭环电路进行了分析，并通过实验得出了分岔和混沌相图。
本文对电网运行于孤岛模式时，恒功率负载条件下连接在储能设备两端的DC-DC双向变换器的工作特性进行分析，通过简化直流微网系统模型，用数学方法建立DC-DC变换器在不连续工作状态下的离散映射，推导出迭代方程，并计算出理论上稳定工作状态下反馈系数的范围，最后通过仿真和实验发现了DC-DC变换器电路中输出电压和电感电流的分岔和混沌现象。
直流微网结构如图1所示，其主要由4个基本部分组成：① 连接在直流微网和主电网之间的三相DC-DC双向变换器，其通过隔离开关连接到直流母线上；② 储能设备(用蓄电池表示)；③ 分布式发电源(用光伏电池表示)；④ 阻性负载和恒功率负载。 蓄电池通过Boost双向变换器连接到直流母线上，Boost双向变换器有2个作用：控制蓄电池能量流动和维持直流母线电压稳定。由于双向变换器两端为非线性负载阻抗，可以将之等效为恒功率负载，据此来分析直流母线电压的非线性特性[8-9]。
图1 直流微网结构
当直流微网脱离主电网、运行在孤岛模式下时有2个主要的电源：① 光伏电池，通常运行在最大功率点跟踪(MPPT)模式下。② 蓄电池，它通过Boost双向变换器连接到直流母线上。光伏电池的输出取决于天气状况，但是对于稳定的气候条件，在一段时间内可以认为光伏发电源向微网中注入恒定的功率，即可以视之为恒功率电源(CPSs)，功率用Ps表示，恒功率负载功率用PL表示。此外，蓄电池的动态特性很慢，可以视之为直流电压源。因此，本文不考虑这2个电源的动态特性。
设光伏电池发出功率Ps和负载消耗功率PL之和为P，即P=Ps+PL，规定Ps <0，PL>0。在孤岛模式下，直流微网简化模型如图2所示，其中C为母线对地电容，L为传输线电感，rc为电容寄生电阻。
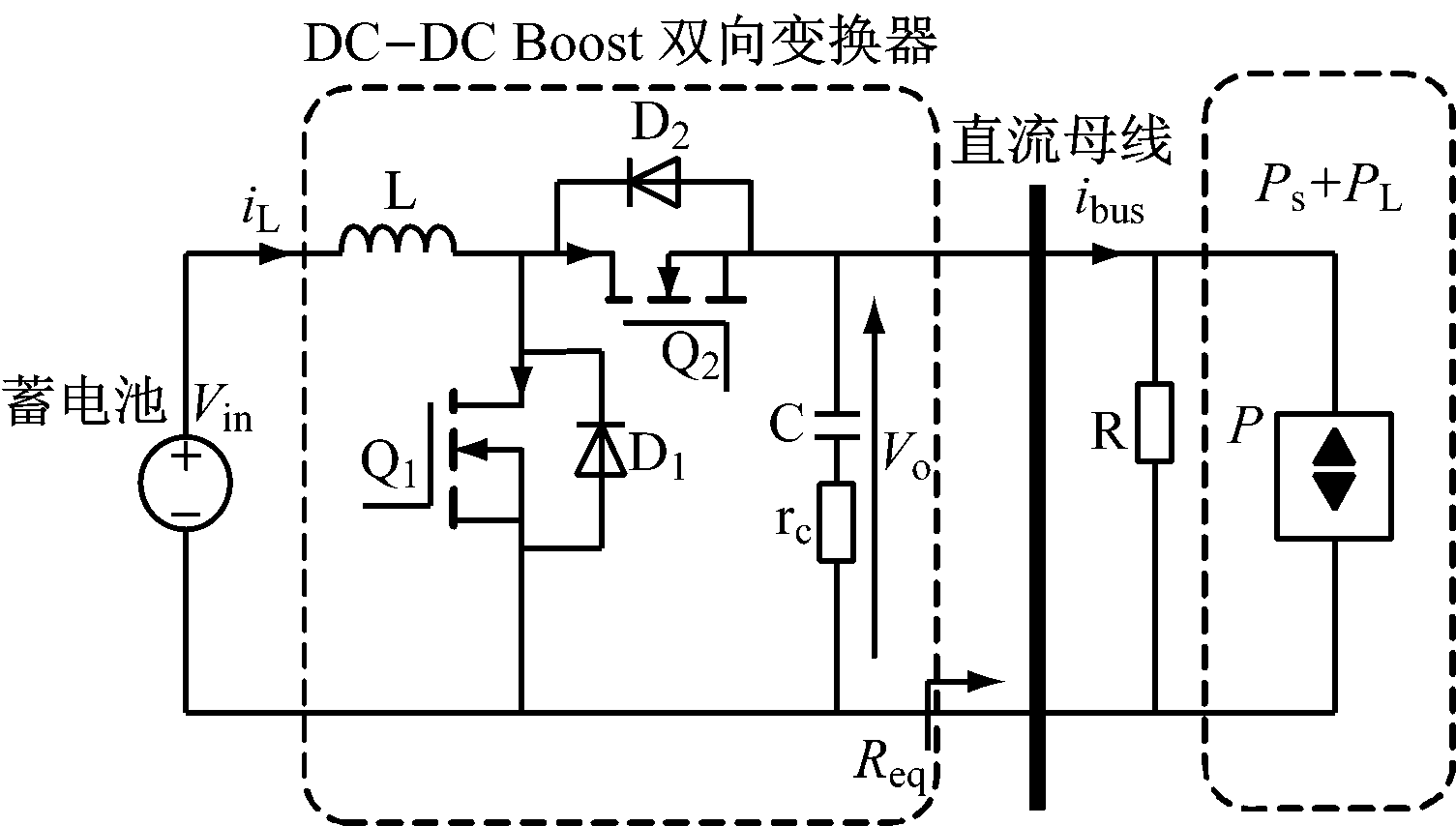
图2 孤岛模式下直流微网简化模型
从简化模型可得直流母线电流ibus和等效负载Req公式：
(1)
(2)
式中:Vo为母线电压(负载电压);R为负载阻抗。
对于不同的负载，Vo-ibus特性曲线如图3所示，其中箭头表示负载阻抗R的变化方向。当P≤0时，阻抗微增量dVo/dibus>0，即电压的增加(减小)会导致电流的增加(减小)；当发出功率小于负载消耗功率即|Ps|<PL时，也即P>0 时，尽管瞬时阻抗总是正的(Req>0)，但是阻抗的微增量却是负的(dVo/dibus<0)，这就是恒功率负载的负阻抗特性。
图3 不同的P和R下Vo-ibus特性曲线
根据参考文献[10]，将恒功率负载等效为一个闭环Buck电路，恒功率负载的等效模型如图4所示。本文不计开关管、电感和电容寄生电阻消耗的能量，通过闭环调节使得R0两端的电压
o恒定，从而使得功率
o/R0恒定。
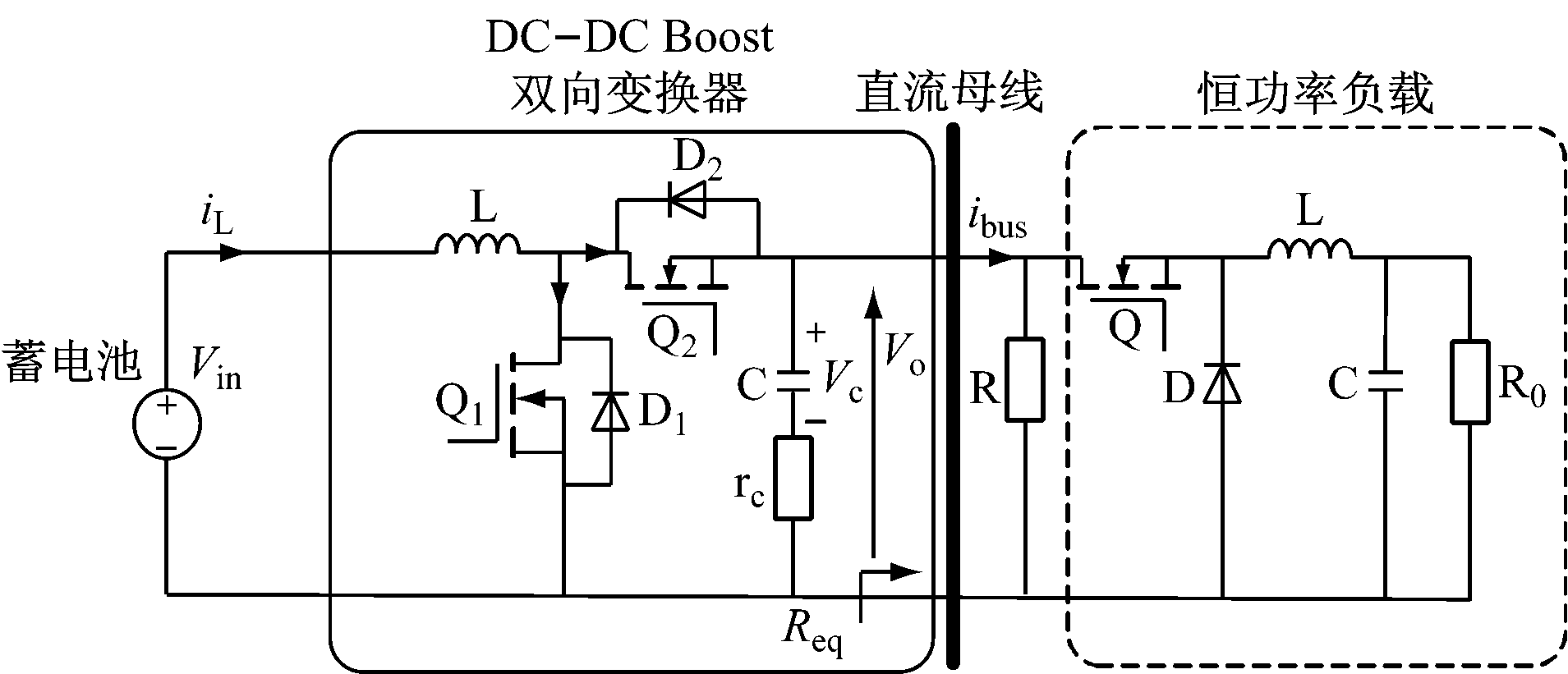
图4 恒功率负载等效模型
对于Buck电路而言，根据输入功率和输出功率相等以及输入电压、输出电压和占空比之间的关系，即UiIi=UoIo和Uiγ=Uo(γ为占空比)，由戴维南定理可求出其输入等效电阻Ri=R0 /γ2，即可以将恒功率负载看作一个非线性电阻，将电路进一步等效为图5，其中iL为电感电流；Vc为滤波电容电压；Vref为电压反馈参考电压；D为电路稳定工作时开关的占空比；dn为第n个开关周期动态占空比。当电路稳定工作时，dn=D，Δdn为第n个开关周期的占空比变化量。
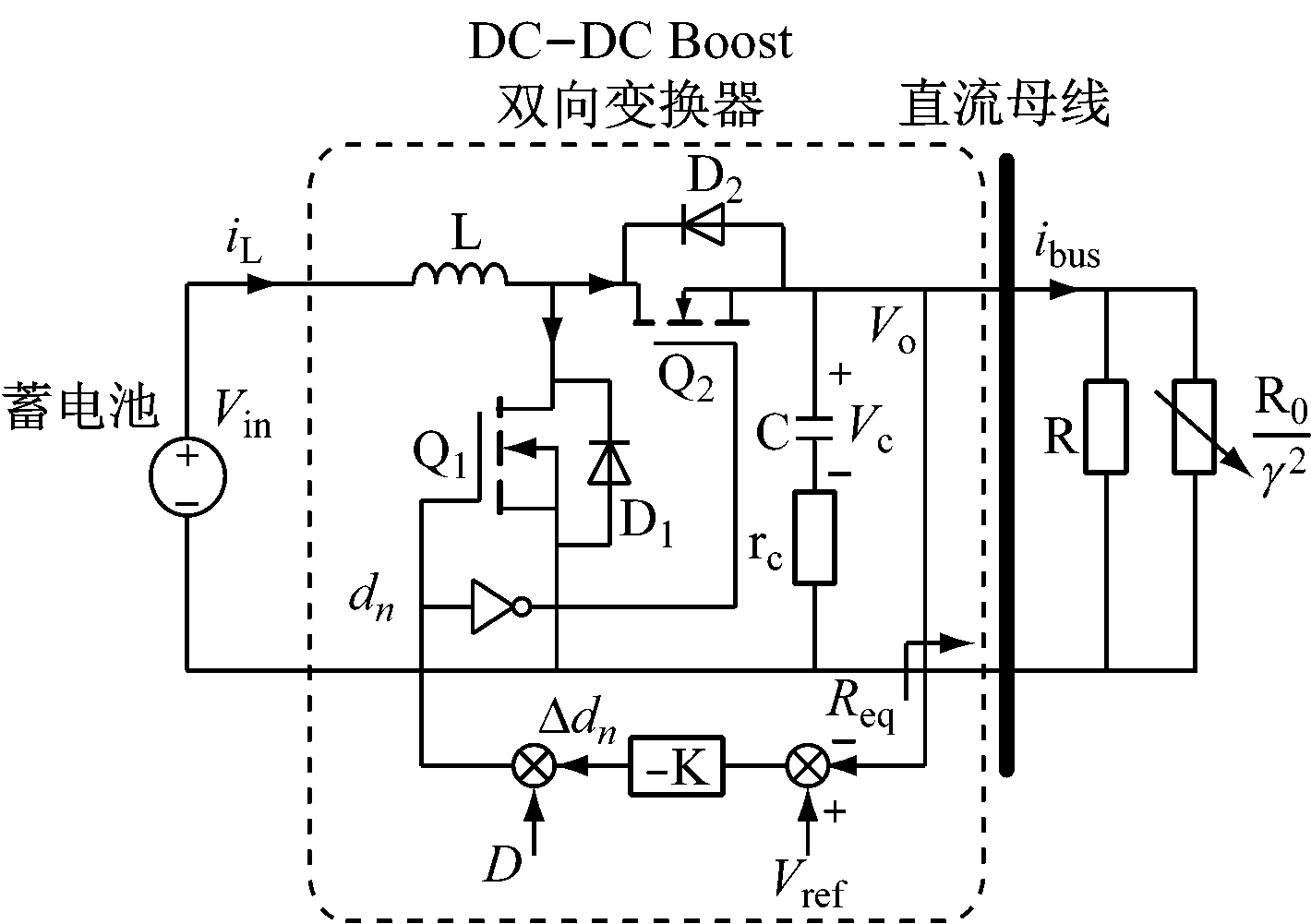
图5 恒功率负载简化模型
令x=[Vo iL]T，变换器工作在不连续运行模式时，电路有3种不同的线性工作模态：① Q1导通，Q2关断，此时电感储存能量。② Q2开通，Q1断开，此时电感释放能量，给电容充电,并为负载供电。③ Q1 和Q2关断，电感能量完全释放，下一个周期还没有到来，电流断续。其状态方程如下：
(3)
式中：E为输入电压;tn为第n个周期Q1导通时间
n是第n个周期Q1关断、Q2导通时间；t″n为从Q1和Q2关断到下一个周期到来的时间；tc为模态1的工作时间；td为模态2的工作时间；te为模态3的工作时间。
式(3)的系数矩阵如下：
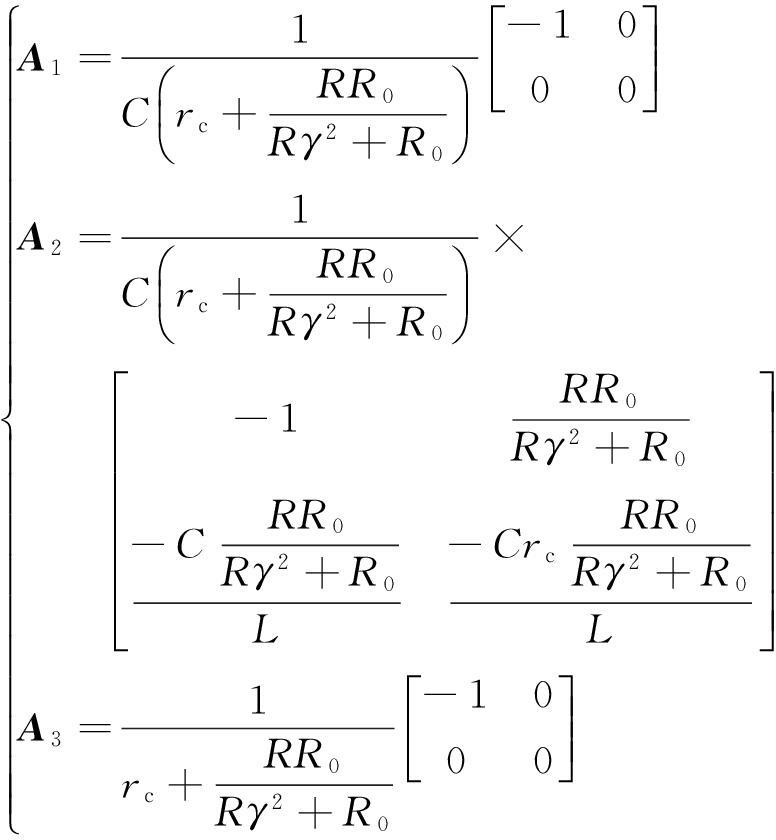
(4)
(5)
由图5可得第n个开关周期占空比：
(6)
式中：k为反馈系数;xn=Vc(tn)=Vc(nT),其中Vc(tn)为第n个周期负载电压,T为开关管周期。
在每个开关周期进行1次状态变量的采样，得到序列x(tn+1)，其离散迭代方程为
x(tn+1)=
(7)
Φm(ξ)=
(8)
式中:τ为时间变量;I为泰勒级数常量;ξ为泰勒级数变量。
取序列x(tn+1)泰勒级数前3项得到近似的离散迭代方程(式(9))，这在一定程度上可以简化对DC-DC双向变换器稳定性的分析，同时其精确度也满足本文的要求。
(9)
当tn<t< 
时，电感电流iL以斜率E/L增加到最大值imax；当
时，电流以斜率(u-E)/L减小到0，所以有
(10)
式中:u为输出电压变量。
由式(3)—式(6)，可将式(7)近似简化为[11]
(11)
式中:
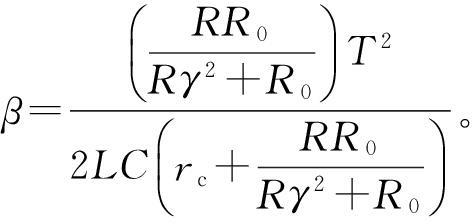
在闭环系统中，最基本的要求是保持系统的稳定性。当任何干扰叠加到稳定工作点时，都应该最终减小到0。通常判断点X处是否稳定，主要考虑点X处Δxn+1泰勒级数的展开式：
(12)
如果扰动比较小，在x=X处，∂f(x)/∂x的幅值决定系统的稳定性。在x处的偏导用λ表示。为了简化分析，假定0<dn<1，则在稳定点的邻域内，可以忽略扰动饱和非线性的影响。对于一个稳定的闭环系统，有一个与之对应的反馈值k，且偏导数λ的绝对值小于1,结合式(11)可得
(13)
本文关注λ=-1时的分岔情况，此时若λ继续减小，则X点处有可能发生谐波振荡，因此λ=-1时，反馈系数的临界值为
(14)
仿真参数设置：频率f=3 kHz，输入电压E=17 V，输出电压Vo=31 V，R=10.8 Ω，P=90 W，L=205 μH,C=222 μF，rc=0.15 Ω，D=0.33。恒功率负载中，
于输出电压基本维持恒定，所以在恒功率负载等效模型中，由式(12)可计算出：
(15)
式中dn=D-k(xn-X)。
对式(15)求偏导可得
0.515 7-24.4k
(16)
由式(16)可以计算出k=0.062。离散迭代方程仿真结果如图6所示，初始时反馈系数k较小，系统处于稳定状态。当k=0.06时，电压出现分岔现象。随着反馈系数k的增大，每个反馈系数k对应2个电压值，由图6可以看出，电压波动虽然不大，但分岔现象已经很明显。继续增大反馈系数k，电压值将出现四周期分岔现象，最后进入混沌状态，无规律可循。
图6 离散迭代方程仿真结果
为了更直观地调节反馈系数，反馈环节采用闭环模拟电路。二级Buck电路只需保持功率恒定即可，因此采用较为方便的数字PI闭环控制。实验电路如图7所示。
图7 实验电路
图7中反馈系数k计算公式为
(17)
式中：Rf为调节比例电阻；R1，R2为分压电阻；R3为运算放大器输入电阻；VH，VL分别为锯齿波的峰值和谷值。
实验波形如图8所示，左侧为输出电压和电感电流的波形图，右侧为电压电流的关系相图。初始时，反馈系数较小，系统处于稳定状态，只有一个极限环，随着反馈系数的增加，逐渐出现周期分岔现象，最后进入混沌状态。
实验结果验证了随着反馈系数k的变化，电压和电流从稳定逐渐过渡到分岔及混沌状态的过程。由于设计电路时存在寄生参数，会产生一定系统误差，使得实验波形与仿真波形不能够完全吻合，但不影响本文的实验结果。
分析了直流微网的结构和特点，并将其简化成恒功率负载模型；对DC-DC双向变换器工作状态进行分析，建立了不连续模态下的离散映射，理论上计算出电路稳定运行时反馈系数的变化范围。通过仿真和实验验证了理论推导的正确性。在直流微网系统中应该选择合适的参数，以免出现分岔乃至混沌等不稳定现象，使得系统失衡甚至崩溃。
(a) k=0.05
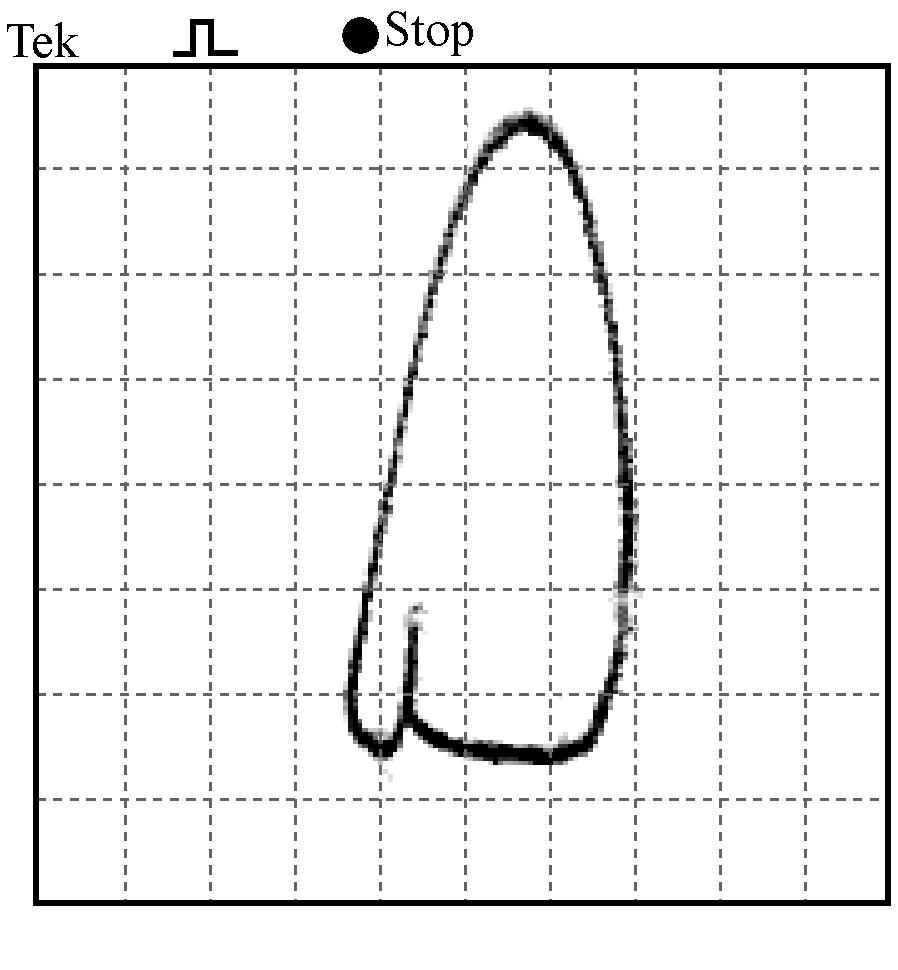
(b) k=0.06
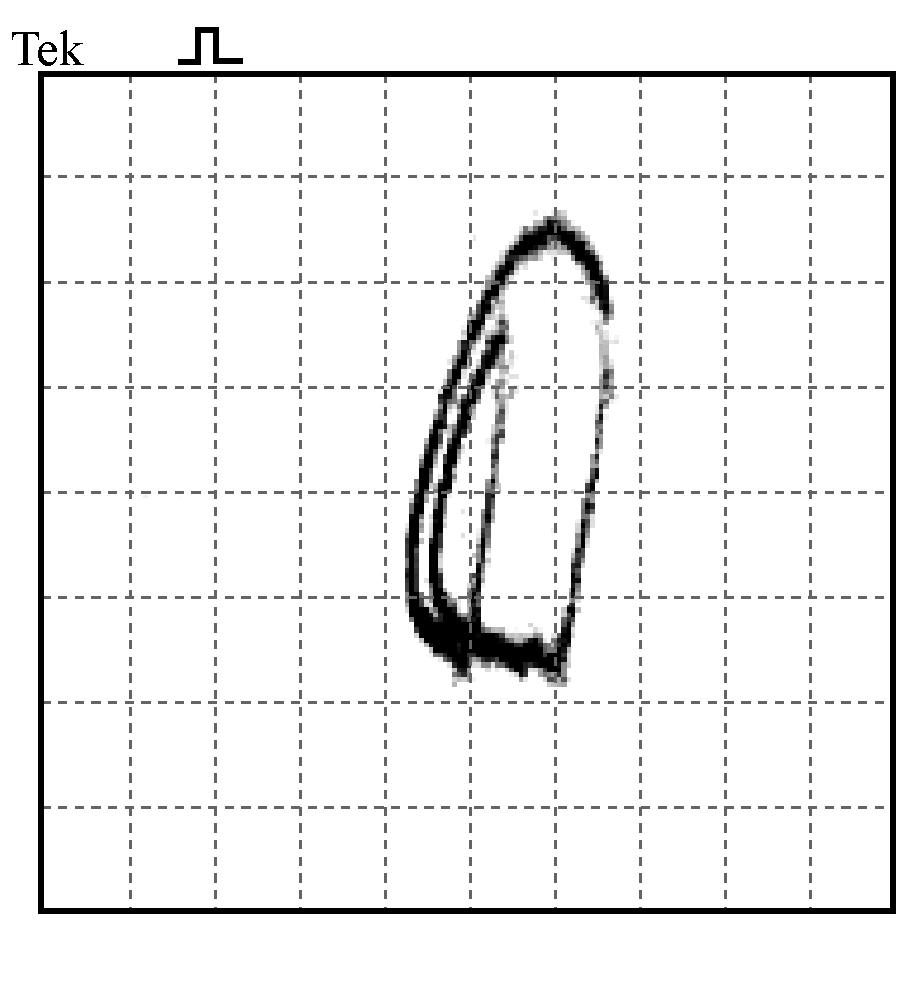
(c) k=0.1
(d) k=0.13
图8 k取不同值时的电压、电流波形及其相图
参考文献：
[1] BOROYEVICH D, CVETKOVIC I, DONG DONG,
et al. Future electronic power distribution systems: a contemplative view[C]//12th International Conference on Optimization of Electrical and Electronic Equipment, Basov, 2010: 1369-1380.
[2] XU C D, CHENG K W E. A survey of distributed power system-AC versus DC distributed power system[C]//4th International Conference on Power Electronics Systems and Applications, Hong Kong, 2011:1-12.
[3] HAROUN R, CID-PASTOR A, EL AROUDI A, et al. Synthesis of canonical elements for power processing in DC distribution systems using cascaded converters and sliding-mode control[J]. IEEE Transactions on Power Electronics, 2014, 29(3):1366-1381.
[4] EMADI A, KHALIGH A, RIVETTA C H, et al. Constant power loads and negative impedance instability in automotive systems: definition, modeling, stability and control of power electronic converters and motor drives[J]. IEEE Transactions on Vehicular Technology, 2006, 55(4):1112-1125.
[5] DU W, ZHANG J, ZHANG Y, et al．Stability criterion for cascaded system with constant power load[J]. IEEE Transactions on Power Electronics, 2013,28(4):1843-1851．
[6] 王春芳,王开艳,李强.Buck变换器仿真模型及分岔与混沌研究[J].系统仿真学报,2007,19(24):5824-5826.
[7] 张波,曲颖.BUCK DC/DC变换器分岔和混沌的精确离散模型及实验研究[J].中国电机工程学报,2003, 23(12):102-106.
[8] TAHIM A P N, PAGANO D J, PONCE E. Nonlinear control of boost bidirectional converters in stand-alone DC microgrids[C]// IEEE 51st Annual Conference on Decision and Control, Maui, 2012: 3068-3073.
[9] 原永滨,徐滨海,张晓俊.船舶电力系统恒功率负载稳定性仿真研究[J].船舶工程,2011,33(6):49-52.
[10] TSE C K. Flip bifurcation and chaos in three-state boost switching regulators[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1994, 41(1): 16-23.
ZHANG Yong， XU Ruidong， LI Tao， XU Shanyu, WANG Long
(School of Information and Electrical Engineering, China University of Mining and Technology,
Xuzhou 221116, China)
Abstract：The DC micro-grids architecture based on multistage power converter was studied, the research method of constant power load was proposed and the simplified model of DC micro-grids was built. According to the simplified model, the discrete mapping with DC-DC bidirectional converter operating in intermittent mode was built, and the iterative equation and computational formula of feedback factor in stable condition were given. The bifurcation waveform between output voltage and feedback factor was obtained according to iterative equation. Simulation and experiment results show that by increasing the feedback factor, the circuit will work from stable condition to bidirectional point and run into chaos eventually.
Key words:direct current micro-grids; bidirectional power converter; constant power load; discrete mapping; bifurcation
中图分类号：TD61
文献标志码：A 网络出版时间：2016-01-26 15:48
文章编号：1671-251X(2016)02-0061-06
DOI:10.13272/j.issn.1671-251x.2016.02.016
张勇，徐瑞东，李涛，等.恒功率负载下DC-DC双向变换器分岔现象研究[J].工矿自动化，2016,42(2)：61-66.