夏辉丽1, 郭亚男1, 余发军1,2
(1.中原工学院 信息商务学院, 河南 郑州 451191;
2.武汉科技大学 冶金自动化与检测技术教育部工程研究中心, 湖北 武汉 430081)
摘要:针对现有基于特征频率识别的矿物传送设备故障诊断方法存在易受强噪声干扰的问题,提出了基于稀疏分类算法的矿物传送设备故障诊断方法。首先,利用计算机测取设备已知故障类型的振动信号,并对其进行傅里叶变换;然后,以傅里叶变换系数构造训练字典,将待测故障类型的振动信号傅里叶变换系数在该训练字典上进行稀疏分解,求取稀疏系数;最后,利用重构信号最小误差判别故障类型。仿真和测试结果表明,该方法能有效诊断出矿物传送设备中轴承的故障类型,为煤矿传送设备的故障监测提供了一种新方法。
关键词:矿物传送设备; 故障诊断; 稀疏分类; 傅里叶变换
煤矿生产运输过程中,传送设备起着将矿物自动传送至目标地点的作用,因此,保证其正常运行对整个生产运输环节至关重要。然而,由于长期受重载工况和外侵灰尘的影响,煤矿中的传送设备极易发生故障,特别是传动轴承及传动齿轮等关键部件发生故障的概率更高。一旦滚动轴承的内外环或齿轮间有外侵物落入,在重载工况下很容易产生故障,所以,对此类设备进行故障监测与诊断对保障煤矿安全正常生产至关重要。
现有煤矿传送设备的故障诊断方法有铁谱分析法[1]、温度监测法[2]和振动监测法[3]等。铁谱分析法利用磁性方法把混于润滑油中的铁质磨粒分离出来,根据磨粒形态尺寸的差异性确定故障部位,但目前对磨粒差异性判断还没有形成科学客观的理论。温度监测法则根据传送设备的温度进行状态监测,如参考文献[2]利用红外技术对煤矿传送系统进行温度保护,但这一方法只能保护设备,并不能诊断故障。振动监测法是最常用的故障诊断方法,其根据设备的振动信号故障特征频率进行故障诊断,但生产背景噪声严重干扰故障特征成分的提取,并且某些设备的故障特征频率往往不可知。
针对以上方法存在的问题,笔者提出了基于稀疏分类算法[4]的矿物传送设备故障诊断方法。该方法利用不同故障类型下振动信号的波形差异性进行故障诊断。首先,利用快速傅里叶变换将设备的振动信号转换至频域,用已知故障类型傅里叶系数建立训练字典,然后对待测信号在该训练字典上进行稀疏分解,利用重构信号最小误差进行故障类型的判别,克服了利用故障特征频率判别故障类型的劣势,为煤矿传送设备的故障监测提供了一种有效方法。
假设矿物传送设备有C种已知故障类型,令A=[A1,A2,…,AC]为振动信号训练集合,Ai为第i种(i=1,2,…,C)故障的子训练集合,y为待测故障类型的振动信号测试样本,则利用稀疏分类算法对y进行归类包含如下步骤:
步骤1:对测试样本y在字典A上进行稀疏分解,即
(1)
式中:α为稀疏分解系数向量;γ为惩罚因子;![]() 1表示求α的L1范数,即
1表示求α的L1范数,即![]() 。
。
步骤2:利用稀疏分解系数重构待测信号,根据重构误差最小值进行归类,即
(2)
式中:![]() i为
i为![]() 中对应的第i种故障类型的稀疏系数子向量。
中对应的第i种故障类型的稀疏系数子向量。
由稀疏分类算法可以看出,该方法是利用同类样本具有最小的稀疏重构误差这一基本理论实现归类的,这一点与线性Fisher分类器[5]具有相似的原理。区别在于稀疏分类算法是利用信号稀疏分解思路实现的,具有极大的自适应性和非线性优点,而线性Fisher分类器则直接利用向量类间距进行超平面线性划分,对非线性归类问题无能为力。
稀疏分类算法是L1范数的最优化问题,可以借助于目前广泛采用的稀疏编码算法求解其稀疏系数。常用于求解L1范数的基追踪算法有l1ls [6]和SLEP[7]等,由于SLEP具有全局最优值和运算速度快等优点,所以本文选用SLEP算法对矿物传送设备振动信号进行稀疏编码,其具体实现过程参见参考文献[7],这里不再赘述。
在矿物传送设备的易损坏部件(如轴承和齿轮箱)的周围安装加速度传感器采集振动信号,通过信号线将振动信号传送至监控室的计算机上,并进行存储和分析,以监控当前设备的运行状态。然而,一方面加速度传感器的采集频率很高,且采集的振动信号往往包含不同强度的背景噪声;另一方面,整个系统的转速及负载具有不确定性,因此,采集的振动信号是一种典型的非平稳信号,这意味着如果直接利用已知故障类型的振动信号构造训练字典,噪声和振动信号起始采样点会严重影响稀疏分类算法的性能。
为了解决以上问题,需先对各种故障类型的振动信号进行傅里叶变换,将其转换至频域,再进行稀疏分解。振动信号v的离散傅里叶变换定义为
(3)
式中:Fv为离散傅里叶变换的系数向量;m和M分别为振动信号采样点数和离散傅里叶变换总点数(M≤m)。
利用各已知故障类型的振动信号傅里叶变换系数的模向量构造训练字典(式(4)),并将待测振动信号y转换至频域,利用其模向量在训练字典A上稀疏分解(式(5)),最后,利用式(2)进行故障类型识别。
![]()
(4)
![]()
(5)
基于稀疏分类算法的矿物传送设备故障诊断方法步骤如下:
步骤1:采集已知故障类型的振动信号,并利用离散傅里叶变换将这些振动信号转换至频域。
步骤 2:利用变换系数模向量构造训练字典。
步骤3:将待测故障类型的振动信号变换系数模向量在训练字典上进行稀疏分解。
步骤4:找出重构误差最小的类别,并以此进行故障类型判别。
为了分析基于稀疏分类算法的矿物传送设备故障诊断方法的性能,建立4种仿真信号分别模拟传送设备中轴承的4种常见的故障类型,即正常、内环故障、外环故障和滚动体故障。其中,正常工况用标准差为1的高斯白噪声模拟;内环故障和滚动体故障工况分别用调幅频率为0.2 Hz和0.3 Hz的周期性脉冲模拟;外环故障用等幅的周期性脉冲模拟,4种工况仿真信号波形如图1所示。
利用本文方法对该4种工况仿真信号进行分析:首先,对每种仿真信号加入信噪比(SNR)为-2~2 dB的高斯白噪声,使每种仿真信号数为50个,用该200个信号构成训练字典;其次,利用离散傅里叶变换将每个信号转换至频域;最后,随机选择其中任一信号在训练字典上进行稀疏分解,并进行重构,找出重构误差最小的故障类别,即为该信号所属的故障类型。每种仿真信号试验30次,取其正确率的平均值作为最后的识别率,其结果如图2所示。

(a) 正常工况

(b) 内环故障
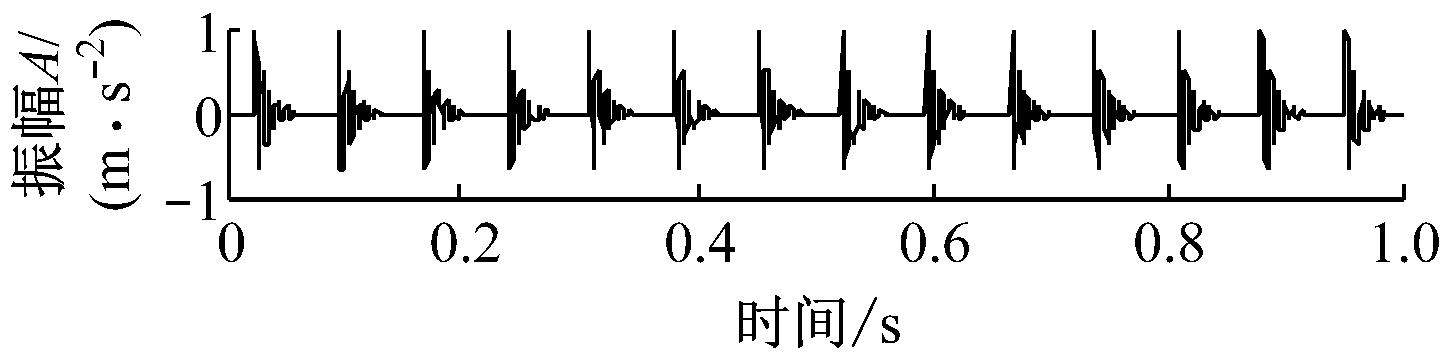
(c) 外环故障

(d) 滚动体故障
图1 4种工况仿真信号波形

图2 4种工况仿真信号识别率随信噪比变化关系曲线
由图2可以看出,4种工况仿真信号的识别率都受信噪比的影响,随着信噪比的增加,正确率明显增加,当信噪比为1 dB以上时,故障诊断的正确率都在82%以上,因此,所提方法可以作为传送设备中轴承故障诊断的方法,对噪声具有一定的免疫性。
为了进一步验证所提方法的有效性,将该方法应用到美国西储大学设备监测实验室的轴承振动数据集[8]上。该数据集包含0.213, 0.427, 0.640,0.853 cm 4种单点故障大小,轴承的型号为6205-2RS。用本文方法分析该种轴承的1种正常工况、3种外环故障、4种内环故障和4种滚动体故障,共12种故障类型。每种故障类型的振动信号采样频率都为12 kHz,采样点都为2 048个,每种故障类型都随机选取50个振动信号,共计600个振动信号构造训练字典,在剩余的振动信号中选择30个作为测试样本。分别用本文方法与支持向量机[9]方法对该测试样本集进行分类识别,诊断正确率见表1。
表1 本文方法和支持向量机方法的诊断正确率

由表1可以看出,利用本文方法和支持向量机方法的设备轴承故障诊断数据集分类正确率都在80%以上,随着故障点尺寸的增加,诊断正确率也明显增加,故障点尺寸越大,诊断越准确;本文方法在故障点的正确率比支持向量机方法高5%左右。
在本文方法中,惩罚因子γ对诊断结果有重要的影响,图3显示了轴承故障诊断数据集分类正确率随惩罚因子γ的变化规律。

图3 轴承故障诊断正确率与惩罚因子γ变化关系曲线
由图3可看出,当γ∈[0.000 1,0.8]时,轴承故障诊断正确率几乎不受惩罚因子γ的影响;但当γ趋于0或1时,诊断正确率会迅速下降。这意味着只要保持惩罚因子γ在[0.000 1,0.8]区间,其对诊断正确率的影响可以忽略。
基于稀疏分类算法的矿物传送设备故障诊断方法以矿物传送设备易损坏部件(轴承)为分析对象,首先将设备振动信号转换至频域,再利用频域稀疏分类算法对不同故障类型的振动信号进行归类。对4种仿真工况下的故障类型振动信号和西储大学实验室轴承振动数据分别进行分析,并与支持向量机方法对比,结果验证了基于稀疏分类算法的矿物传送设备故障诊断方法的有效性和优势,为煤矿传送设备的故障监测提供了一种新的有效方法。
参考文献:
[1] 杨树莲,刘春潮. 铁谱监测技术在煤矿设备故障诊断中的应用[J].中国煤炭, 2002,28(4):42-43.
[2] 余安徽,黄小剑,白志青.基于红外技术的煤矿传送系统温度保护中的研究[J].科技信息,2012,29(21): 438-439.
[3] 刘永斌.基于非线性信号分析的滚动轴承状态监测诊断研究[D].合肥:中国科学技术大学,2011:8-9.
[4] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2009,31(2):210-227.
[5] 陈才扣,杨静宇. Fisher大间距线性分类器[J].中国图像图形学报,2007,12(12):2143-2147.
[6] KIM S J, KOH K, LUSTIG M, et al. A method for large-scale L1-regularized least squares[J]. IEEE Journal on Selected Topics in Signal Processing, 2007,1(4):606-617.
[7] LIU J, JI S, YE J. SLEP: sparse learning with efficient projections[R]. Phoenix: Arizona State University, 2009.
[8] Case Western Reserve University. Case Western Reserve University bearing data center website [EB/OL].[2015-09-20]. http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.
[9] QI Zhiquan, TIAN Yingjie, SHI Yong. Robust twin support vector machine for pattern classification[J].Pattern Recognition, 2013,46(1):305-316.
XIA Huili1, GUO Yanan1, YU Fajun1,2
(1.College of Information and Business,Zhongyuan University of Technology,Zhengzhou 451191,China;
2.Engineering Research Center of Metallurgical Automation and Measurement Technology of
Ministry of Education,Wuhan University of Science and Technology,Wuhan 430081,China)
Abstract:In view of the problem that the existing fault diagnosis methods based on feature frequency identification for mineral transmission equipments are susceptible to strong noise, a new fault diagnosis method based on sparse classification algorithm for mineral transmission equipment was proposed. Firstly, vibration signals for the known fault types of equipment are collected by computer and transformed by Fourier transformation. Then, the Fourier transformation coefficient vectors of test vibration signal are sparsely coded on a dictionary, which is constructed by merging the Fourier transformation coefficient vectors of the known vibration signals, so as to get sparse coefficient. At last, the fault types of the test samples are labeled by identifying their minimal reconstruction errors. The simulation and test results demonstrate that the method can effectively diagnose the fault type of bearing of mineral transmission equipment, which provides a novel method for fault monitoring of transmission equipment in coal mine.
Key words:mineral transmission equipment; fault diagnosis; sparse classification; Fourier transformation
中图分类号:TD67
文献标志码:A 网络出版时间:2016-01-26 15:46
文章编号:1671-251X(2016)02-0043-04
DOI:10.13272/j.issn.1671-251x.2016.02.011
夏辉丽,郭亚男,余发军.基于稀疏分类算法的矿物传送设备故障诊断方法[J].工矿自动化,2016,42(2):43-46.