崔传波1,2, 蒋曙光1,2, 王凯1,2, 邵昊1,2, 吴征艳1,2
(1.中国矿业大学 安全工程学院, 江苏 徐州 221116;
2.煤炭资源与安全开采国家重点实验室, 江苏 徐州 221116)
摘要:由于通风网络中分支的风量相互影响,针对改变分支风阻重新分配风量的方法会造成风量减小较快的分支风量不能满足最低需风要求的问题,基于风量调节基本理论建立了风量可调度模型,提出了基于风量可调度的矿井风量调节方法。该方法利用风网解算确定被调分支风阻可调范围,进而从定量角度求得需风分支风量可调度。利用该方法计算风量可调度便于选择最佳风阻调节分支以及确定风阻调节范围与风量变化量。
关键词:风量调节; 灵敏度; 风网解算; 风量可调度
随着矿井的生产推进,矿井的通风网络结构、阻力分布、通风设施、通风动力等都会随之变化,致使通风系统网络的分支风量也发生变化[1]。当通风系统网络分支风量的变化超过一定范围时就会引起瓦斯积聚、瓦斯超限等问题,威胁矿井安全生产[2]。为了满足某一特定工作点的用风需求,需要对其他分支进行风阻调节。
近年来,国内外许多学者对风阻调节展开了深入研究[3-7]。Shamir等[8]在流体网络研究中引入灵敏度分析,将其与网络解算结合,避免了某些参数变化所引起的不必要的迭代计算;吴奉亮等[9]用灵敏度优选矿井风量调节点及调节参数;史东涛等[10]引入灵敏度衰减率来研究风量调节的风阻临界值。但是,利用风量灵敏度分析法只能确定各分支对某个分支的敏感程度,通过调节需调分支中敏感度较大的分支风阻来改变该分支风量、压力分配[10],没有从定量的角度确定需调分支风阻调节范围以及调节该分支后各分支风量变化范围。
为此,笔者提出了基于风量可调度的矿井风量调节方法,以风量调节理论为基础,建立风量可调度模型,利用风网解算确定被调分支风阻可调范围,进而从定量角度求得需风分支风量可调度。
矿井通风网络内风量调节过程是按照供风要求,使网络内风流从不平衡到平衡的过程。风量调节必须遵循网络风流变化的基本规律。根据风量平衡定律,网络内任意节点处各风路风量的代数和为零,即
(1)
式中dqi为各风路风量的变化量。
对于风压平衡定律,综合考虑网络风路风阻、风量的变化以及有无通风机等多种情况,可得
(2)
式中:ri为网络内风路风阻;tg θi为通风机特性曲线的斜率。
2.1 风量可调度概念
矿井通风系统局部风量调节过程中,为了便于选择风量调节的最佳分支,引入风量可调度这一新概念来量化分支j风阻变化对分支i风量的影响大小。
灵敏度dij用于表述分支j的风阻Rj变化对分支i风量Qi的影响程度,风量可调度与灵敏度关系为
(3)
式中:ΔRj=Rj-Rj0 ,为分支j的风阻变化量;ΔQi=Qi-Qi0,为分支i的变化量,即分支i相对于分支j的风量可调度。
2.2 风量可调度的计算
灵敏度衰减率[10-11]表示通风网络灵敏度随风阻变化的情况,用tij表示:
(4)
由式(4)可知,在通风网络参数变化时,风网工作状态也会变化,但是变化快慢程度不同。因此,灵敏度dij随风阻Rj的改变而变化。通过大量通风网络试验计算和模拟分析发现,灵敏度dij和风阻Rj之间总是符合如下关系式:
(5)
式中:a,b,c为常数,可通过数据分析拟合求得。
由式(3)和式(5)可得
(6)
对分支j使用增阻调节法,则分支i的风量变化量由分支j的风阻调节范围决定。假设分支j的风阻可调范围为Rj∈[u,v],利用面积积分公式对式(6)两边Rj积分,可得风量可调度为
(7)
2.3 风阻调节范围的确定
对分支j进行增阻调节时,各个分支的风量Qi随风阻Rj的变化而变化。利用通风网络解算程序,分支j风阻变化一次,就会获得一组各个分支的风量Q=[q1,q2,…,qn]T。通过大量通风网络试验计算和模拟分析发现,风量Qi和风阻Rj之间总是符合如下关系式:
(8)
利用通风网络解算程序,可以解得分支j风阻变化时各个分支的风量Qi。在调节分支j的风阻时,整个通风网络的各个分支风量都会受到影响,与分支j处于并联或串联关系的分支,其风量随Rj的改变变大或变小。为了满足各个分支的正常工作生产要求,风量随Rj变化而变小的分支,其风量不能低于最低需风量。因此,分支j的风阻Rj调节范围[u,v]主要取决于风量随Rj变化而变小的分支。
通风网络G=(V,E)如图1所示,|V|=7,|E|=11,风阻列向量R=[1.373 4,1.471 5,1.177 2,0.981,0.784 8,2.943,0.588 6,3.924,4.120 2,5.886,2.246 7]T,风阻单位为Ns2/m8。分支11安装有通风机,通风机风压特性曲线:hf=1 046.3+5q-0.85q2。假设分支8需要增加2 m3/s的风量,选择增阻法调节风阻,使风路8的用风地点风量满足要求,按照上述算法选择可调分支。
3.1 通风网络的解算
在已知各个分支风阻和通风机风压特性曲线的前提下,运用Matlab编程解算通风网络G=(V,E),可得此时各个分支风量Q=[8.655 1,8.192 8,4.561 2,5.399 8,7.535 5,2.425 4,11.629 5,5.218 4,4.093 9,2.793 0,16.846 8],单位为m3/s。
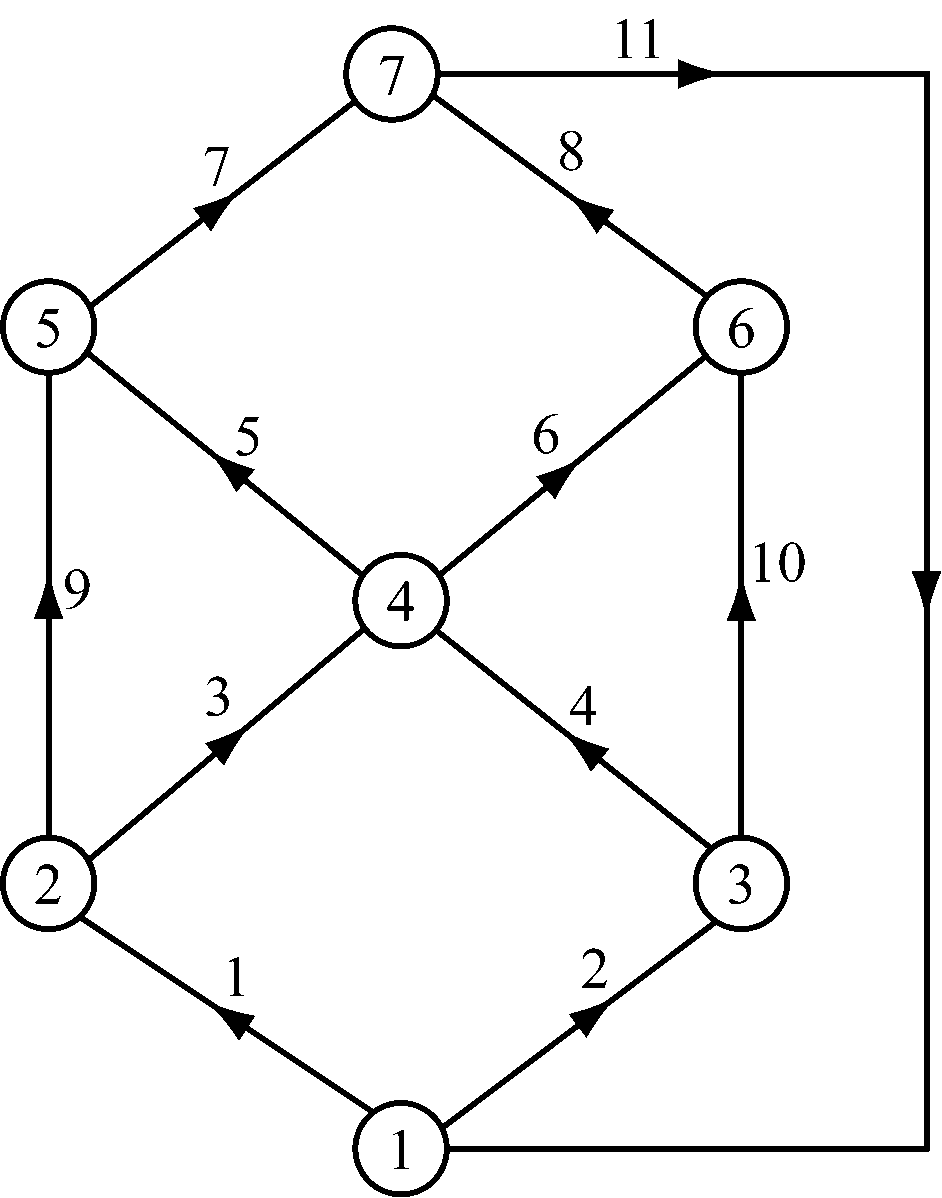
图1 通风网络
3.2 分支7风阻调节范围的确定
选择最佳可调分支时,以调节分支7的风阻R7为例。随着分支7的风阻R7增大,其他各个分支的风量随之变化,利用Matlab进行风网解算,求得不同R7下的其他各个分支的风量。随着分支7风阻增大,各个分支风量增大或减小,如图2所示。
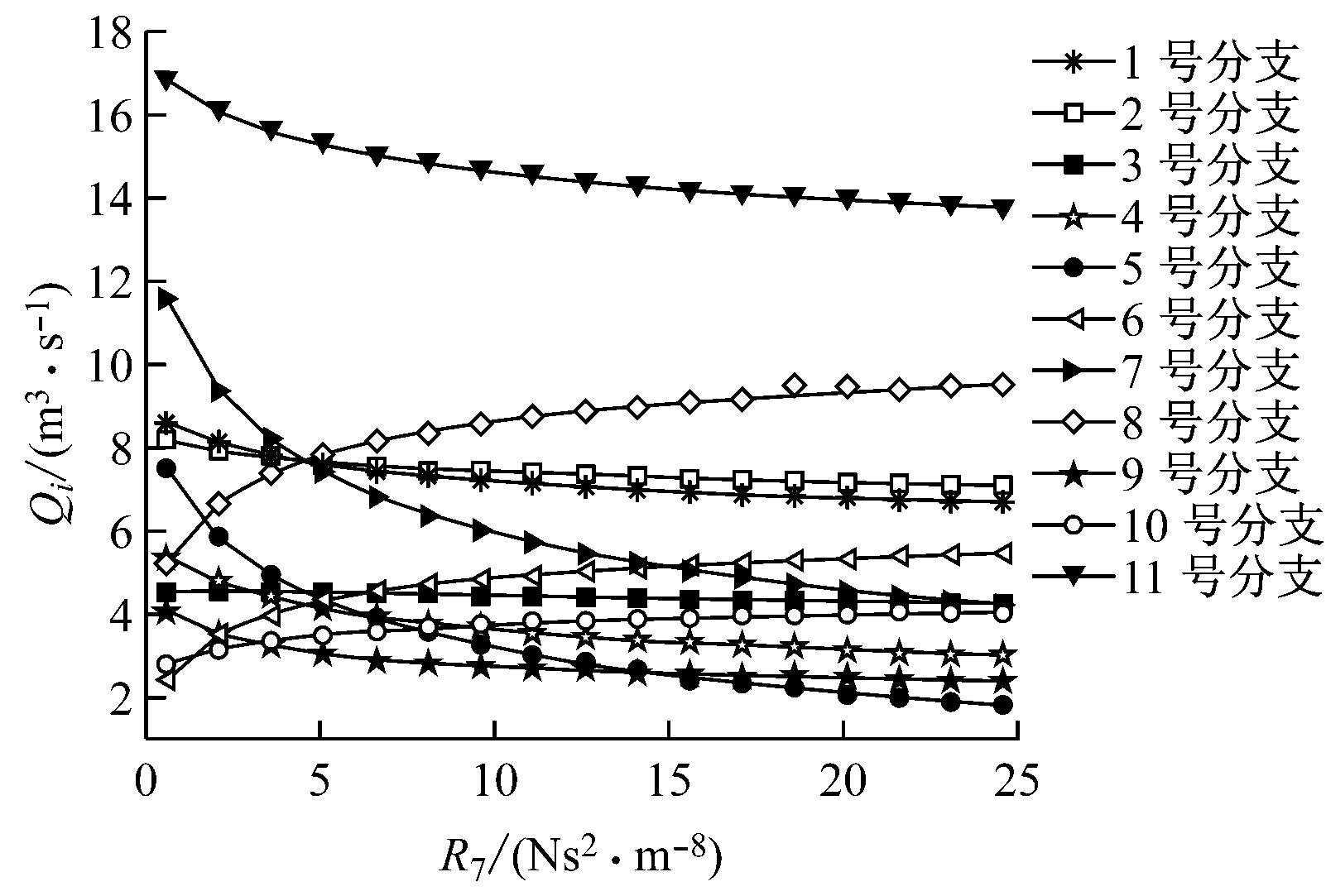
图2 随风阻R7增大时的各个分支风量变化曲线
为了满足各个分支的生产需要,风量减小的分支其风量不能低于最低需风量。因此,在确定分支7的风阻调节范围时,主要考虑风量减小的分支其风阻是否满足要求,其中随着分支7风阻增大而风量减小的有分支1、2、4、5、7、9、11。由于分支3受分支7风阻变化影响很小,故不予考虑。运用Origin画出分支1、2、4、5、7、9、11的风量随分支7的风阻R7增大而减小的曲线,如图3所示。
煤矿井下各个用风地点的需风量不仅受瓦斯涌出浓度的影响,还受作业人数、炸药量、机械设备的影响。为了满足井下各个用风地点的需风要求,每个分支风量不能低于最低需风量。计算得到的各个分支最低需风量见表1。
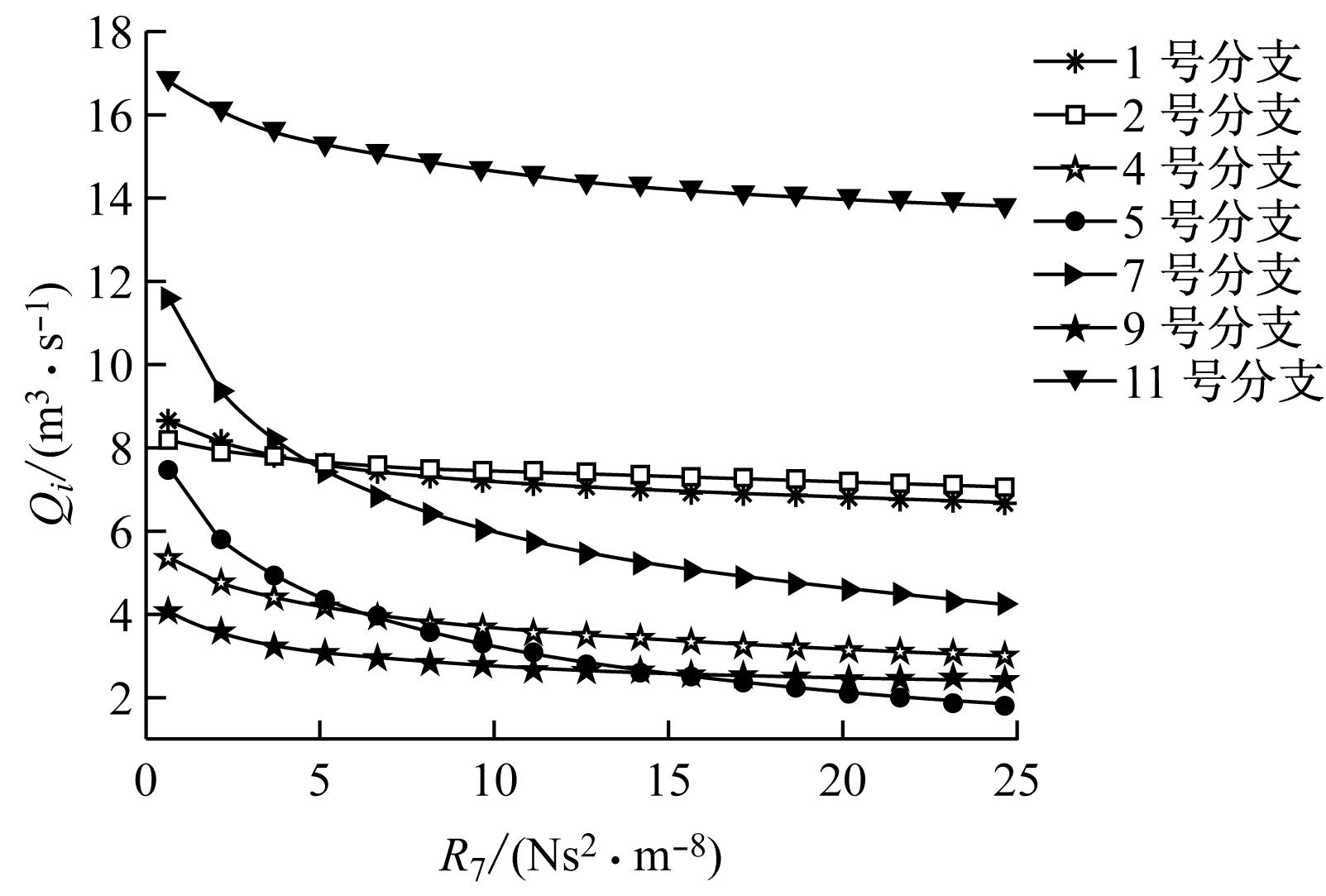
图3 随风阻R7增大而分支风量减小的曲线
表1 各个分支最低需风量

从图3和表1可以看出,随分支7风阻增大,分支4、5、7、11的风量减小较快,且相比于其他分支最先低于最低需风量,以分支4、5、7、11的最低需风量为横实线画图,所得图形如图4所示。

图4 最低需风量与分支风量变化曲线
由图4可知,各个分支的风量变化曲线与其最低需风量Qmin直线相交的交点中,R7最小值是分支5的风量变化曲线与其最低需风量Q5min=5.213 7 m3/s的交点。下面确定交点的风阻值。随着分支7的风阻增大,分支5的风量减小,风量Q5和风阻R7之间总是满足式(8)。运用通风网络解算程序,可得风量Q5与灵敏度d87随风阻R7变化的数据,见表2。
利用Matlab软件的Power幂函数拟合处理后可得风量Q5随风阻R7变化的曲线,如图5所示。
分支5的风量Q5与分支7的风阻R7的关系为
![]() +26.02
+26.02
(9)
表2 风量Q5与灵敏度d87随风阻R7变化的数据

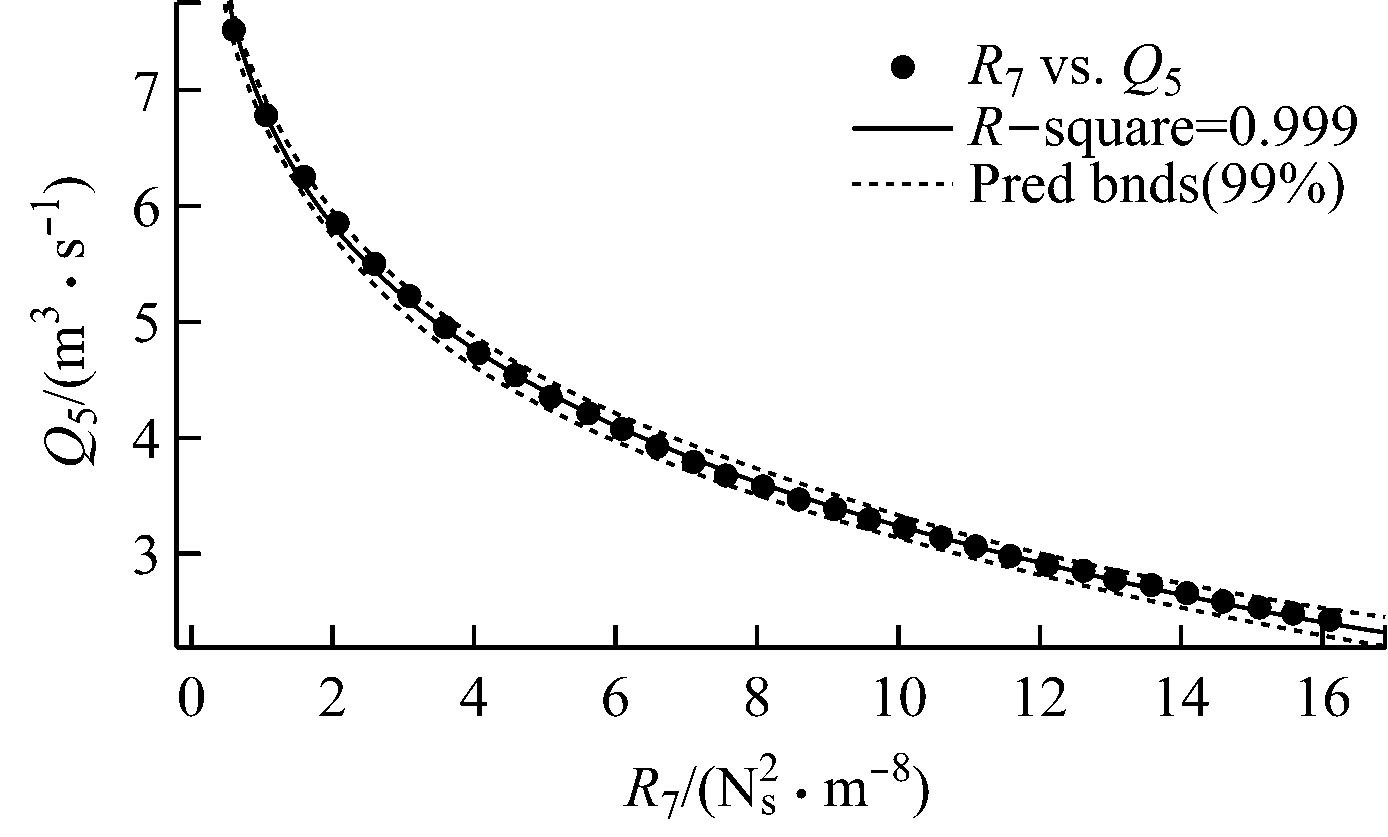
图5 风量Q5随风阻R7变化的曲线
将分支5的最低需风量Q5min=5.213 7 m3/s代入式(7),可得R7=3.023 5 Ns2/m8,即为分支7风阻的最大可调值。R7初始值为0.588 6 Ns2/m8,则分支7的风阻调节范围[u,v]=[0.588 6,3.023 5]。
3.3 分支7风量可调度的计算
在确定分支7的风阻调节范围后,利用式(5)求解风量可调度。运用Matlab编程求得灵敏度d87随分支7的风阻R7变化的数据(表2)。利用Matlab软件的Power幂函数拟合处理后可得灵敏度d87随风阻R7变化的曲线,如图6所示。
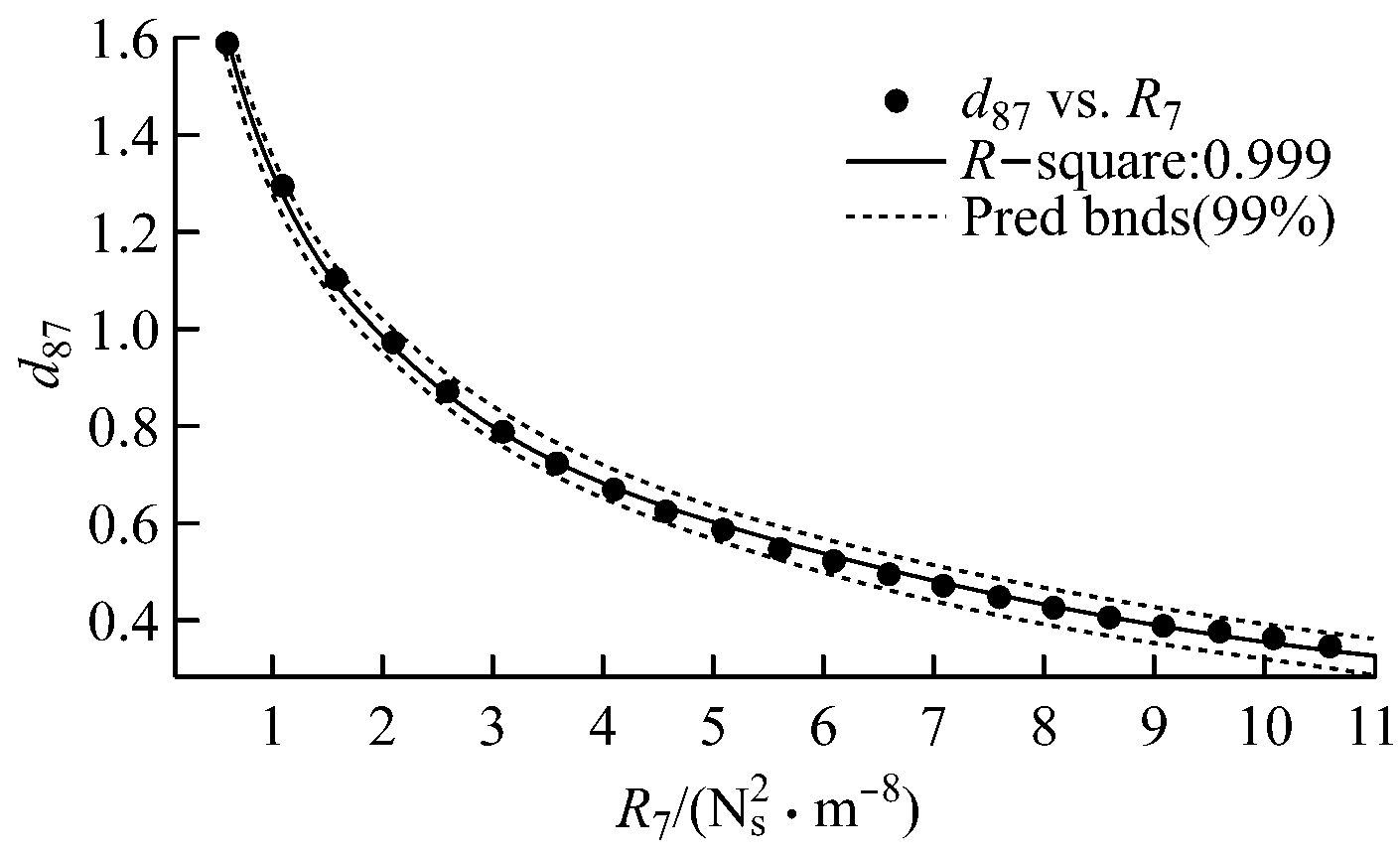
图6 灵敏度d87随风阻R7变化的曲线
灵敏度d87与风阻R7的关系为
(10)
式中d87表示分支7风阻改变对分支8风量的影响。
通过确定的分支7风阻调节范围[u,v]=[0.588 6,3.023 5],利用式(5)、式(8)求出分支8的风量可调度ΔQ8=2.628 8 m3/s,由此对分支7增阻调节,能使分支8增大风量为2.628 8 m3/s,满足分支8增加风量2 m3/s的要求。因此,只要对分支7增阻调节就可使分支8的风量达到需风要求。
基于风量可调度的矿井风量调节方法利用Matlab编程,通过风网解算求出各个分支风量。对大量数据模拟分析和实验研究发现,风量可调度ΔQi与灵敏度dij之间总是符合关系式ΔQi=dijΔdi。该方法从定量的角度直观体现出调节分支j的风阻对分支i的风量影响大小,便于矿井井下风量调节时可调分支的选择以及风阻调节范围的确定。
参考文献:
[1] 黄元平.矿井通风[M].徐州:中国矿业大学出版社,1990:47-79.
[2] HOWARD L H, MUTMANSKY J M, RAMANI R V, et al. Mine ventilation and air conditioning[M].New York: Wiley, 1997:35-40.
[3] 周心权,吴兵,杜红兵. 矿井通风基本概念的理论基础分析[J].中国矿业大学学报, 2003,32(2):133-137.
[4] 王树刚,王继仁,洪林. 矿井正常和灾变时期通风网络解算的数学模型[J].辽宁工程技术大学学报,2003,22(4):436-438.
[5] 刘惠德,连英立,艾婷.基于组件式GIS的矿井通风安全管理与决策支持软件的开发[J].工矿自动化,2008,34(6):69-71.
[6] WANG Y J. Solving mine ventilation networks with fixed and non-fixed branches[J].Mining Engineering,1990,42(12):1342-1346.
[7] 曲素荣,贾燕茹. 矿井主通风机变频调速系统技术改造[J].工矿自动化,2009,35(8):86-88.
[8] SHAMIR U, HOWARD C D D. Water distribution systems analysis[J]. Journal of Hydraulics Division Asce,1968,94(1):219-234.
[9] 吴奉亮. 用灵敏度优选矿井风量调节点及调节参数[J].矿业安全与环保,2011,38(5):1-3.
[10] 史东涛.基于灵敏度的风量异常与风量调节的分析研究[D].西安:西安科技大学,2008.
[11] 贾进章,刘剑,倪景峰. 通风系统可靠性稳定性及灵敏性数学模型[J].辽宁工程技术大学学报,2003,22(6):725-727.
CUI Chuanbo1,2, JIANG Shuguang1,2, WANG Kai1,2, SHAO Hao1,2, WU Zhenyan1,2
(1.School of Safety Engineering, China University of Mining and Technology, Xuzhou 221116, China;
2.State Key Laboratory of Coal Resources and Safe Mining, Xuzhou 221116, China)
Abstract:Due to the air volume of branch of ventilation network is influenced by each other, and the method of change branch wind resistance to airflow distribution will be caused the air volume of decreased faster branch airflow cannot meet the minimum requirements, the air volume dispatchable model was set up based on airflow condition theory, an adjustment method of air volume based on air volume dispatchable model was proposed. The adjustment method uses ventilation network solution to calculate adjustable range of branch wind resistance, and obtains the air volume of branch from quantitative angle. Using the method to calculate air volume is convenient to choose the most adjustable branch and confirm the wind resistance adjustment range and variation of air quantity.
Key words:air volume adjustment; sensitivity; ventilation network solution; air volume dispatchable model
作者简介:崔传波(1990-),男,山东泰安人,硕士研究生,主要研究方向为煤矿井下应急救援、矿井通风等,E-mail:cbcui1999@163.com。 夏辉丽(1980-),女,河南舞钢人,讲师,主要研究方向为计算机技术应用、信息处理技术等,E-mail:2727616857@qq.com。
基金项目:国家自然科学基金青年基金资助项目(51404263);江苏省自然科学基金青年基金资助项目(BK20130203, BK20140187)。 国家自然科学基金项目(61174106);河南省高等学校科研重点项目(15B510017)。
收稿日期:2015-10-12;修回日期:2015-11-19;责任编辑:张强。 2015-10-21;修回日期:2015-11-24;责任编辑:张强。
中图分类号:TD723
文献标志码:A 网络出版时间:2016-01-26 15:45
文章编号:1671-251X(2016)02-0039-05
DOI:10.13272/j.issn.1671-251x.2016.02.010
崔传波,蒋曙光,王凯,等.基于风量可调度的矿井风量调节[J].工矿自动化,2016,42(2):39-43.